基于社会网络分析的指标群划分及群间关系研究＊

程 豪，易丹辉，牟宗毅

（1.中国科协创新战略研究院 北京 100012；2.中国人民大学应用统计科学研究中心 北京 100012；3.长春中医药大学附属医院 长春 130117）

1 引言

随着科技的发展，人与人之间的社交渠道越来越多样，不同的人之间可能存在着不同的关系，同一群人在不同的环境下也可能存在着不同的关系，因此形成了很多错综复杂的网络，比如，社会关系网络、物流网络、互联网、犯罪网络、学术成果引用网络、病毒传播网络等等。这种网络关系不仅形成于“人”与“人”之间，更存在诸多科学领域。比如，生命科学领域中，基因数据的研究与DNA本身的双螺旋结构有很大的关系。具体来说，基因作为具有遗传效应的DNA片段，每个DNA分子上有多个基因，每个基因含有成百上千个脱氧核苷酸。由于不同基因的核糖核苷酸的排列顺序不同，不同的基因就含有不同的遗传信息。因此，研究基因间关系、基因组逻辑结构及程序化表达成为探讨基因逻辑和语言的核心问题。另外，细胞中包含各种复杂的结构，细胞包含细胞膜、细胞质和细胞核三部分。而各部分分别有各自的结构，包含不同的细胞器，这些细胞器构成了一个功能分化的网络结构。

无论是人际关系网络还是生命科学网络，都存在构成网络的基本单位，称为变量、指标或者节点。一般地，网络结构关系可分为如下几种情况：第一，网络中存在因变量，自变量个数不多且相互独立，则会考虑回归模型；当自变量个数较多时，通常会采用变量选择方法，如果变量间存在结构关系，则需要考虑带结构的变量选择，如Group Lasso，MCP等。第二，网络中不存在因变量，常用的方法主要有多元统计方法（主成分分析、聚类分析、因子分析等）、结构方程模型、贝叶斯网络和隐结构。这些方法要求一个变量仅属于一个群体，无法满足同一变量在不同群体里的多重角色。第三，网络中不存在因变量，自变量间存在未知结构关系，上述的方法均会失效。此时只能考虑采用社会网络分析理论，对解释变量间的结构关系进行挖掘和数值化的分析。比如，在由指标节点构成的网络中，社会网络分析方法有助于识别节点角色，有助于探索网络中潜在的结构关系和节点行为，有助于预测网络中的个体或群体的变化，以提供决策支持。

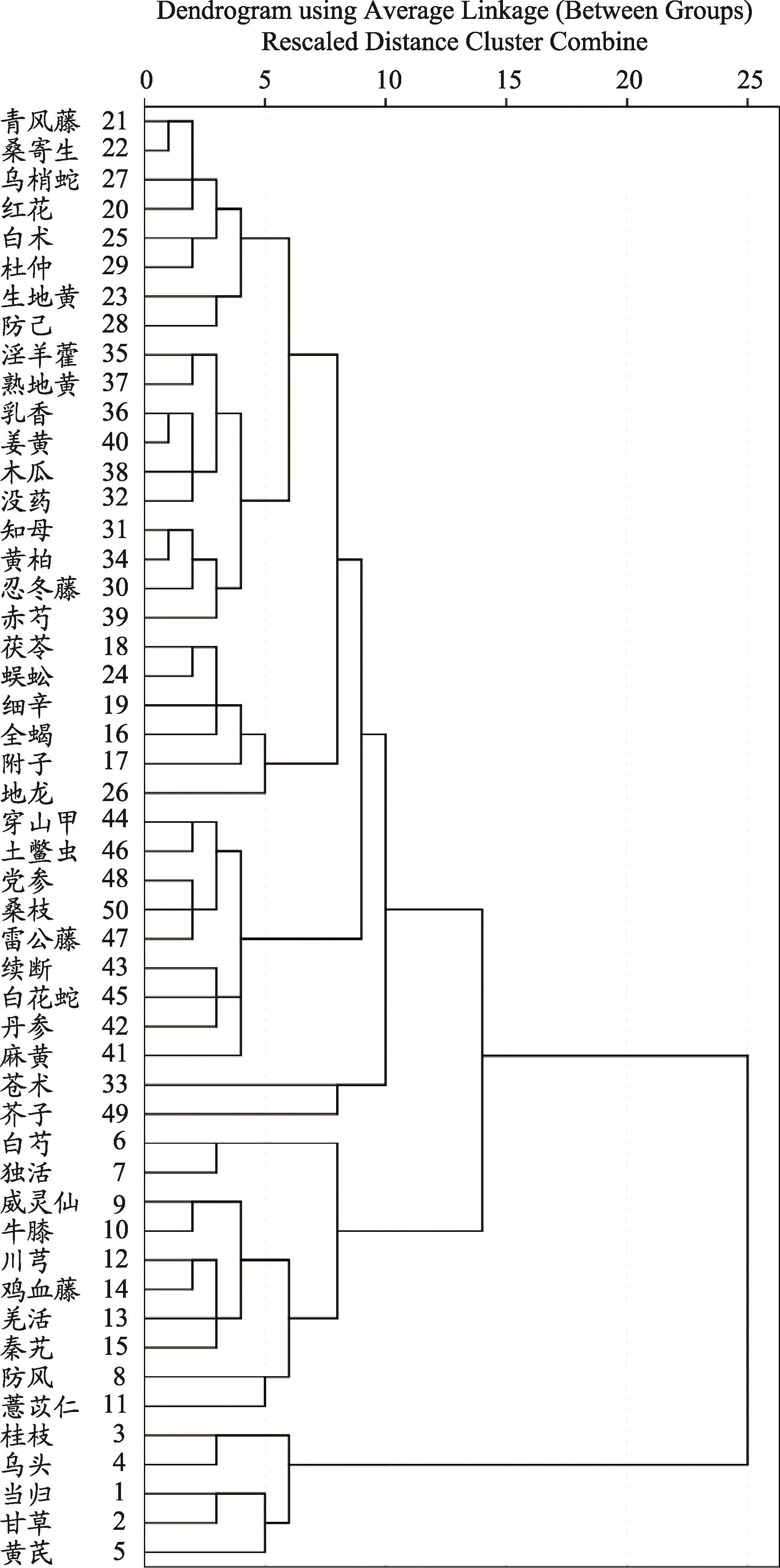
图1 社会网络发展图

2 文献综述

社会网络理论发端于20世纪30年代，由R布朗在群体内部关系结构的研究中提出，是一种新的社会学研究范式。自从20世纪70年代以来，社会网络分析成为社会学、心理学、人类学、数学等领域逐步发展起来的一个研究分支。经由巴恩斯、鲍特、纳德尔、米歇尔、霍曼斯等诸多领域学者的研究和发展，构建了社会网络分析理论，逐步形成一般性的学科。社会网络分析的发展历史如图1所示。

多年来，一些国内外专家一直致力于将社会网络分析理论应用到网络关系测度及划分的问题上。Freeman（1979）总结了度数中心性、接近中心性和中间中心性等测度网络中心性的指标，并分别借助后两个指标刻画获取资源的能力和控制他人的能力。Friedkin（1991）根据网络环境特性，用社会网络分析理论描述行动者在网络中的地位。张存刚、李明和陆德海（2004）归纳关系取向和位置取向两种分析取向及其基本特征。彭小川和毛晓丹（2004）应用社群图和矩阵法概括了BBS群体的基本特征，并深入探讨了各成员地位的形成、意见领袖的特点和群体内部人际交往的特征。李林艳（2004）梳理了社会网络的不同研究取向、形式结构以及社会网络分析的局限。为了进一步研究社区内社区成员的亲属关系，S.Parthasarathy、Y.Ruan和V.Satuluri（2011）通过研究节点及节点间的连接情况，分析同一社区内成员间的网络结构关系。Theodoros Lappas、Kun Liu和Evimaria Terzi（2011）以专家为节点，研究社会网络中专家之间的网络分布和结构关系。

此外，还有一些学者也在动态社会网络分析领域也取得一些研究成果。王飞跃（2005）研究了社会计算与数字网络化社会的动态变化规律。周春光、曲鹏程和王曦（2008）根据隐结构和两阶段聚类法，提出一种新的动态社会网络分析算法。于卓尔、周春光和杨滨等人（2008）基于社会网络的静态和动态特征，研究社会网络中的社区发现问题，并提出适用于静态社会网络的Detstructure算法和适用于动态社会网络的基于衰减策略的融合挖掘算法。陈琼、李辉辉和肖南峰（2010）在节点动态属性相似性的基础上，研究社会网络社区推荐算法。李静永（2012）探讨了动态社会网络社区发现算法研究。杨通辉（2013）研究了基于节点属性变化的个体动态演化过程。

3 指标群划分的数据基础

利用社会网络分析工具划分指标群，必须以关系型数据为基础。因此在分析前，需要利用相似度度量的方法对不同类型的数据间关系先进行数值计算，获得关系型数据。根据数据类型的不同，相似度度量方法如表1所示。

因此，可以将评价不同类型变量相似度的度量方法整理为：

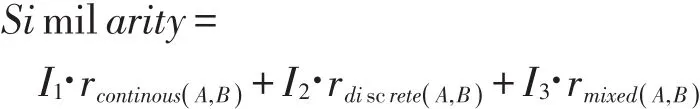
其中，rcontinous(A,B)表示连续性变量(A,B)间的相关系数，rdiscrete(A,B表)示离散型变量(A,B)的相关关系，rmixed(A,B)表示离散型和连续性变量之间的相关关系。而I1、I2、I3均为适性函数。

需要注意的是，在利用上述的三种相关系数对节点间相似性进行测度时，前两种相关系数的取值范围是[-1,1]，第三种相关系数的取值范围为[0,1]。因此，可以考虑取绝对值，判断节点间相关性的强弱，再判断变量间这种相关性的正负。

4 指标群划分的思路及方法

4.1 指标群划分的基本思路

指标群的划分是指根据指标间关系信息，对所有指标节点进行直接离散处理后形成的小群体（称为指标子群），再结合指标子群间的关系，对指标子群进行凝聚所形成的群体。对于一个网络，其复杂度不仅仅受制于网络规模的大小，而且还会受到很多未知的或是已知的局部结构关系的影响。换句话说，对于一个复杂网络来说，其中一定隐含着一些未知的结构模式，对于这些隐含模式的挖掘可以有助于进一步梳理错综复杂的网络结构，提取关键信息，剔除不重要的干扰因素。一个最简单的结构关系就是两两之间的相关性或相似性，在此基础上，通过设置一定的界限，可以对网络中的节点进行简单的划分，形成一些小群体。显然，如果这些小群体之间独立，后面我们称这种情况为”成分”，则从网络的整体角度来看，不存在结构关系，只是一些独立的小群体，而如果小群体间存在不同程度的关系，则整个网络就会形成一个结构关系网络。如果继续研究，根据这些指标小群体间的关系进行聚合，则有形成了介于整体网络和小群体之间的群体，此时的结构关系就变得更为复杂。照此下去，如果一个网络规模足够大，则网络中的结构关系内容就会非常的丰富，而对这种结构关系进行探讨的复杂程度一般是由研究者来控制，只要满足研究者的分析需求，就可以终止对网络的分析。

由此可见，指标群划分的基本思想是“先划分再凝聚”，即从关系型数据出发，指标节点间结构划分首先对网络中所有指标节点离散化，完成了第一次结构划分；其次是对已被离散化的指标子群进行凝聚，完成第二次结构划分。

但是，离散化的程度和凝聚的程度都需要合理的控制。如果过离散化，则会将每个指标节点划分成一个指标子群，同样地，如果过凝聚化，则所有的指标子群又会被凝聚在一个指标群中。无论是哪种情况，都会使分析失效。因此在划分和凝聚的过程中，需要注意的就是选择适当的标尺，来控制指标子群和指标群的规模。而这种标尺的选择会因分析方法的不同而不同。

表1 不同类型变量间相似性度量方法

4.2 测度方法的选择研究

派系是最早被提出的概念，通过对复杂网络进行派系分析，可以将指标节点划分为若干指标小群体，但是，派系分析存在网络结构划分不够稳定等局限，此外，由于派系是建立在指标节点间邻接基础上的，因此忽视了通过一些间接关系连接在一起的指标小群体。

R.J.Mokken提出了n-宗派（n-clan），即任何两点之间的捷径距离都不超过n的一个n-派系（ncliques）。Seidman和Foster（1978）提出k-丛（k-plex）概念，即每个点都至少与除了k个点之外的其他点直接相连；如果一个子图中的全部点都至少与该子图中的k个其他点邻接，则成为k-核（k-core）。这些方法都是根据指标群体内部成员之间关系来对指标节点进行结构划分的。在复杂网络中，如何对各个指标节点进行全面的结构划分，一方面要关注子群内部的关系，另一方面需要比较指标群体内部节点之间的关系强度或频次相对于指标群体内、外部指标节点之间的关系强度或频次。

因此，在分析指标节点间结构关系时，既需要考虑指标群内指标节点间的关系，又需要考虑指标群内外的指标节点间的关系；既要按照一定标准，把一个网络中的各个指标节点分成几个离散的子集，又不能使同一个指标群体内指标节点相距太远；既要实现对指标节点的划分，形成指标子群体，又要研究出不同指标群体之间的关系，实现指标子群体的凝聚，形成指标群体。这样就可以实现对复杂网络中指标节点间结构关系的探讨。

表2 块模型后对结果解释的三个层次

表3 不同指标网络结构设计

综上可以看出，只有块模型才能解决本文的研究问题。块模型的构建包含两步：第一步是把各个指标节点分到各个块中，常用CONCOR方法和Tabu搜索算法；第二步是根据一些标准，确定各个块的取值（1或0）。常用整个网络的平均密度值作为标准，称为α-密度指标。在对指标节点进行块模型分析后，可以从三个层次对结果进行解释，具体见表2。

块模型中最常使用的方法是CONCOR法和Tabu搜索算法。Tabu搜索算法是一种比CONCOR更高级的算法，Tabu搜索算法所遵循的标准是：如果有一个行动者集合，其中的各个行动者的截面的组内方差和最小，Tabu搜索算法就把这样的行动者分为一组。当图的规模较大时，CONCOR方法只能呈现树形图，无法迭代出元素只有1和-1的关系矩阵，因此无法得出指标群的划分结果，而Tabu搜索算法则可以得到具体的指标成群的划分情况，也可以通过迭代出的密度矩阵测度指标群间的关系。

此外，CONCOR只能生成系统决定的“块”的个数，无法人为的设置，而Tabu搜索算法最终划分的“块”数可以提前人为设置，这样可以避免划分多度或者划分不足所造成的指标群体规模太小和太大等划分不均匀、不充分的问题。在实际操作的过程中，可以通过设置几个“块”数，对指标节点进行若干次数的划分，并通过最终的划分结果来确定最优的分块数。

综上所述，本文在对复杂网络进行结构关系划分时，选择较为高级的Tabu搜索算法完成指标节点的划分，形成指标群，并进一步测度指标群间关系。

5 不同指标网络结构的仿真实验

5.1 不同指标网络结构设计

因为现实存在的网络结构千变万化，而且随着网络规模的增加，网络结构会越来越复杂，因此在模拟前需要对社会网络的网络结构进行归类和选择，选择有代表性的社会网络结构进行模拟，经文献查阅可知，无论网络的规模如何，在网络建模方面，社会网络的网络结构可划分为中心网络结构和无中心网络结构，有中心结构的社会网络是指在整个网络中，存在明显的中心节点，所有的节点均是围绕着中心节点进行连接的，无中心结构的社会网络是指没有中心，形状类似与渔网，节点间彼此联系的密度分布较为均匀。因此，本节将对这两种网络结构进行模拟。

5.2 指标群划分及群间关系结果

对于有中心结构的指标网络，借助Tabu搜索算法，经过不断尝试，当划分群个数为5时，指标群的规模比较均匀，划分结果如下所示：

B1-1={x3,x11,x22,x23,x24,x25,x26,x27}；

表4 指标群的密度矩阵及群间关系矩阵

B1-2={x2,x8,x9,x10,x16,x17,x18,x19,x20,x21}；

B1-3={x7,x12,x31,x32,x33,x34,x35,x36}；

B1-4={x6,x13,x15,x37,x38,x39,x40,x41}；

B1-5={x1,x4,x5,x14,x28,x29,x30,x42,x43,x44,x45}；

对于无中心结构的指标网络，借助Tabu搜索算法，经过不断尝试，当划分群个数为6时，指标群的规模比较均匀，划分结果如下所示：

B2-1={x8,x27,x28,x29,x30}；

B2-2={x3,x12,x32,x33,x34}；

B2-3={x1,x9,x10,x11,x18,x35,x36,x37,x38}；

B2-4={x6,x7,x21,x23,x24,x25,x39,x40}；

B2-5={x2,x16,x17,x22,x26,x41,x42}；

B2-6={x4,x5,x13,x14,x15,x19,x20,x31,x43,x44}

不难发现，Tabu搜索算法实现了对指标群的划分，与表3中的指标网络结构图对照发现，Tabu搜索算法的划分结果与直观判断的结果非常接近，说明能够真实反映指标间客观存在的网络结构关系。

对于有中心结构的指标网络，经计算可知，整个网络的密度为0.044，将表4有中心结构部分的密度矩阵中大于0.044的元素赋值为1，小于0.044的元素赋值为0。可以得到右侧有中心结构部分的群间关系矩阵，指标群间关系矩阵中只有对角线元素为1，其余元素全部为0，说明所形成的指标群是完全自反的，即该有中心结构的社会网络形成的指标群间没有关系，而指标群内存在着紧密的联系。换句话说，在这个社会网络中，指标可以被划分为5个指标群，但是这5个指标群间独立无关。对于无中心结构的指标网络，因为整个网络的密度为0.075，将上述矩阵中大于0.075的元素赋值为1，小于0.075的元素赋值为0。由表4下半部分的计算结果可知，指标群间关系矩阵中除了对角线元素为1，还有两处非对角线元素为1，说明所形成的指标群是自反的，但是B 1与B 5相关。因此指标群间的关系如下：B 1与B 5相关，但是其他指标群间都无关。

6 中医症状指标间关系的应用研究

近年来，随着人们生活水平的提高和生活质量的改善，冠心病的发病率和死亡率均明显增加，而且，冠心病患者也越来越趋于年轻化。为了积极控制冠心病的危险因素，西医采用以硝酸酯类药物，钙通道阻滞剂及β受体阻滞剂为治疗基石，配合他汀类药物及多重抗血小板药物，使冠心病的控制率及远期生存率得到一定程度的改善。但是，无论从治疗的经济性，药物的安全性，还是从长期治疗的依从性都没有得到很好的解决。相比之下，中医中药在治疗方面具有有效性、安全性和经济性，但是，由于种种原因，中医的整体观念、辨证论治等个体化治疗的方案较难归纳总结，因此，其疗效评价的差距较大。如何寻找特定疾病的证侯共性，规范指导治疗，提高疗效，成为目前中医科研中亟待解决的问题。

证候属于中医学的范畴，是指一系列有相互关系的症状总称。证素是辨证的基本要素，其内容是根据中医学理论来确定。朱文锋教授将证素的概念引入了辨证新体系。王永炎院士在辨证分型及诊断研究方面也提供了很好的思路，提出了证候要素和应证组合理论。

表5 症状指标的编码

因此，利用中医诊断所获的症状信息，对不同症状间存在的多层次结构关系进行研究，探索证候的可能构成，评价症状在证素构成方面的重要性，成为本文要解决的实际问题，具有一定的应用研究价值。

6.1 数据库说明

本文数据来源于该项调查中发作期数据，调查时间相隔3个月，有效访问了595例患者。数据分为个人信息、相关病史、心绞痛发作特点和症状四部分。其中，症状可以概括为面色、唇色、爪甲色、形态、寒热、汗出、头身胸腹、口渴、口味、饮食、大便、小便、睡眠和舌脉共14个方面。而且，除舌脉外，每个方面下均存在一些症状表征，而且这些症状表征相互平行，比如：面色包括面色恍白、面色萎黄、满面通红、两颧潮红、面色晦暗、面色黧黑、面色无华、面色虚浮8种症状表征，其中，恍白和萎黄不可能同时出现，恍白和晦暗也不可能同时出现等等。表5是对症状指标编码情况的具体说明。

6.2 症状指标划分结果

73个症状指标构成的网络结构关系复杂，如图2所示。很难从图上直观的看出成群情况，因此，需要通过Tabu搜索算法对发作期的症状指标进行结构划分。

对于73个症状指标，Tabu作为一种更加高级的算法，虽然无法直接呈现出从单个指标节点到整个指标节点的过程，但是，可以提前设置最终形成的“块”（block）数k，通过最终形成的指标群体的规模大小来判断划分是否恰到好处。比如，如果划分出现了单个症状指标的指标群，就要考虑是否过度划分（一般要求最小指标群体规模大于等于3，独立指标节点除外，不纳入分析）；如果每个指标群体规模都很大，则需要考虑加大k值，增加划分的充分性。经过对k=10、11、12、13四种情况的划分，可以看出，k=11时，划分的结果较佳，因此，得到下面11个指标群体，又称为“块”。每个块中所包含的的症状指标如下所示：

Block1={x50,x51,x52,x54,x57,x58,x73}={头痛，头晕，耳聋，头身胸腹类-其他，口渴欲饮，口渴喜热饮，失眠}；

Block2={x2,x20,x21,x32,x41,x60,x68}={面色萎黄，肢体困重，肢体麻木，四肢不温，腹胀，口苦，小便频数}；

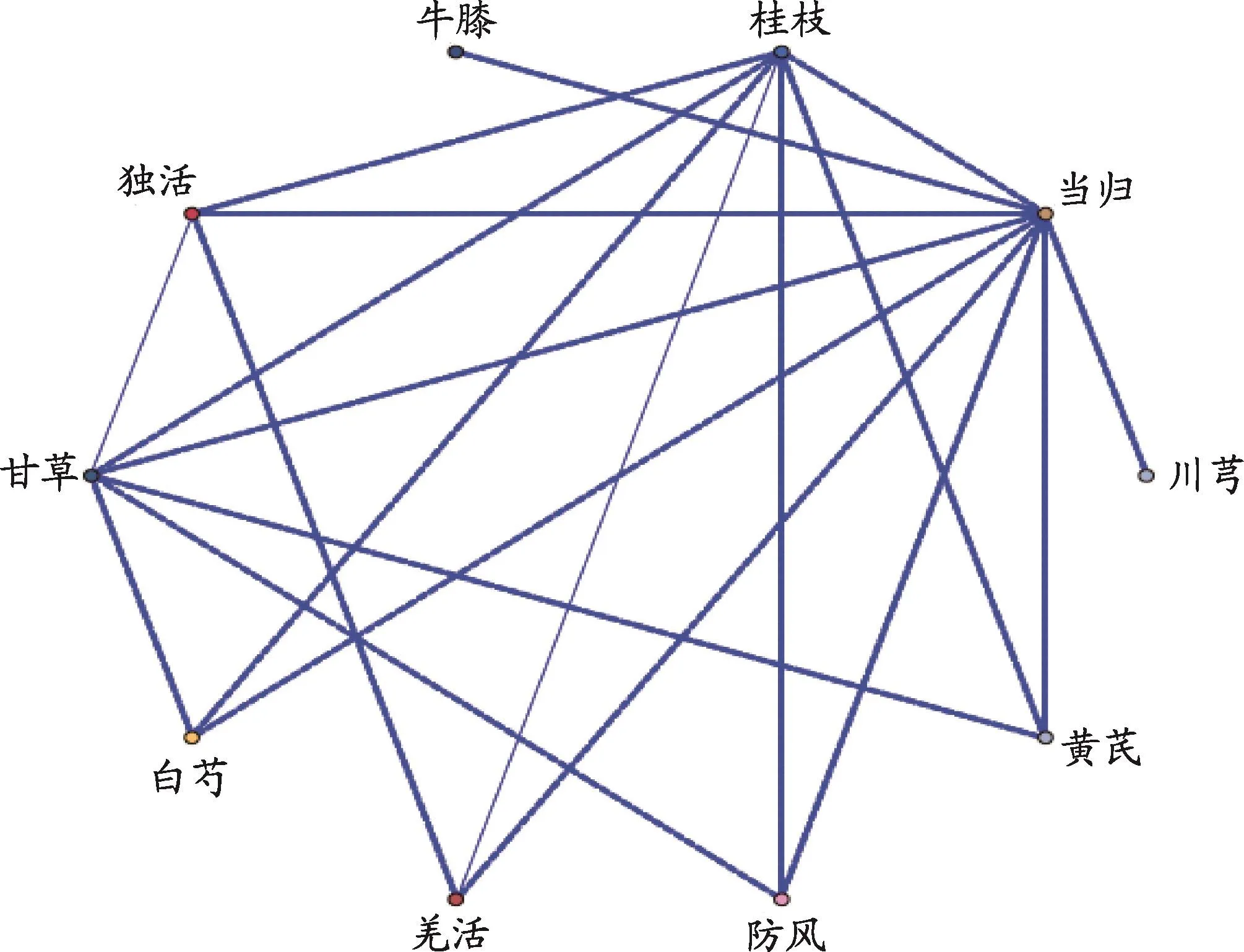
图2 发作期症状指标网络图

Block3={x4,x11,x15,x49,x72}={两颧潮红，唇色紫暗，爪甲色紫，腰膝酸软，小便短赤}；

Block4={x36,x37,x38,x53,x56}={胸痛，心悸，心烦，耳鸣，口渴不欲饮}；

Block5={x8,x18,x19,x24,x25,x26,x27,x30,x46,x59,x67,x70}={面色虚浮，面目浮肿，四肢肿胀，毛发干枯，肌肤甲错，皮肤粗糙，皮肤青灰，潮热，急躁易怒，口淡，小便少，小便涩痛}；

Block6={x6,x16,x43}={面色黧黑，形体肥胖，泛酸}；

Block7={x33,x45,x55}={自汗，善太息，有无口感口渴}；

Block8={x13,x17,x23,x47,x48,x63,x69,x71}={爪甲色青，形体瘦弱，肢冷，协胀，情志抑郁，食少纳呆，夜间多尿，小便清长}；

Block9={x31,x34,x35,x65,x66}={手足心热，盗汗，胸闷，便秘，便溏}；

Block10={x5,x7,x22,x28,x29}={面色晦暗，面色无华，关节疼痛，恶风，恶寒}；

Block11={x1,x3,x9,x10,x12,x14,x39,x40,x42,x44,x61,x62,x64}={面色恍白，满面通红，唇色淡白，唇色深红，唇色青黑，爪甲色暗，暖气，食少纳呆，脘痞，恶心呕吐，口臭，口粘腻，消谷善饥}.

到目前为止，整个症状指标构成的网络被划分成11个指标子群，下一步就需要研究这11个指标子群间的关系，哪些指标子群可以构成指标群。具体请见下面的初始密度矩阵（见表6）：

而整个网络的密度值为0.256，所以对上述原始密度矩阵进行0-1赋值，具体的规则如下：大于0.256的元素赋值1，小于0.256的元素赋值0。表6可得到指标子群（即块）之间的关系。从密度矩阵的非对角线的位置上是否出现1，可以说明指标子群间是否存在关系，具体来说，1表示指标子群间存在关系，0表示指标子群没有关系。因此，存在指标子群间关系的指标群有：{Block1，Block4}，{Block1，Block7}，{Block1，Block10}，{Block2，Block7}，{Block2，Block8}，{Block2，Block10}，{Block3，Block7}，{Block4，Block7}，{Block4，Block9}，{Block5，Block8}，{Block5，Block9}，{Block5，Block10}，{Block6，Block10}，{Block7，Block8}，{Block7，Block9},{Block7，Block10}，{Block8，Block10}。

由下面的图3是指标子群间的结构关系图，可以更加直观的展示出指标子群间的结构关系。

由图3可知，除了症状指标子群11与任何其他的指标子群间无关外，其余10个指标子群间会存在一些关系。经过上述的分析，可以探索出指标子群的构成及指标群间的结构关系。从医学上来讲，通过对症状指标的多层次结构划分，即可解决证候的构成，及证候间存在的结构关系。因为在中医领域中，某种疾病的诊断需要通过望、闻、问、切获得多种症状指标的情况，而不同的症状组合，或是证候组合可以用来判断患者是否某种疾病。

7 结论

真实世界中的网络是普遍存在的，网络中的结构关系是错综复杂的。本文从网络中指标节点间关系角度出发，借助社会网络分析理论中的Tabu搜索算法，主要完成如下几项研究工作：1）提出复杂网络“先划分再凝聚”的分析思路；2）基于大量社会网络分析方法的Tabu搜索算法的选择；3）将纷繁复杂的指标网络划分成若干个指标群以及指标群间关系的测度；4）应用到中医症状指标间关系的讨论。

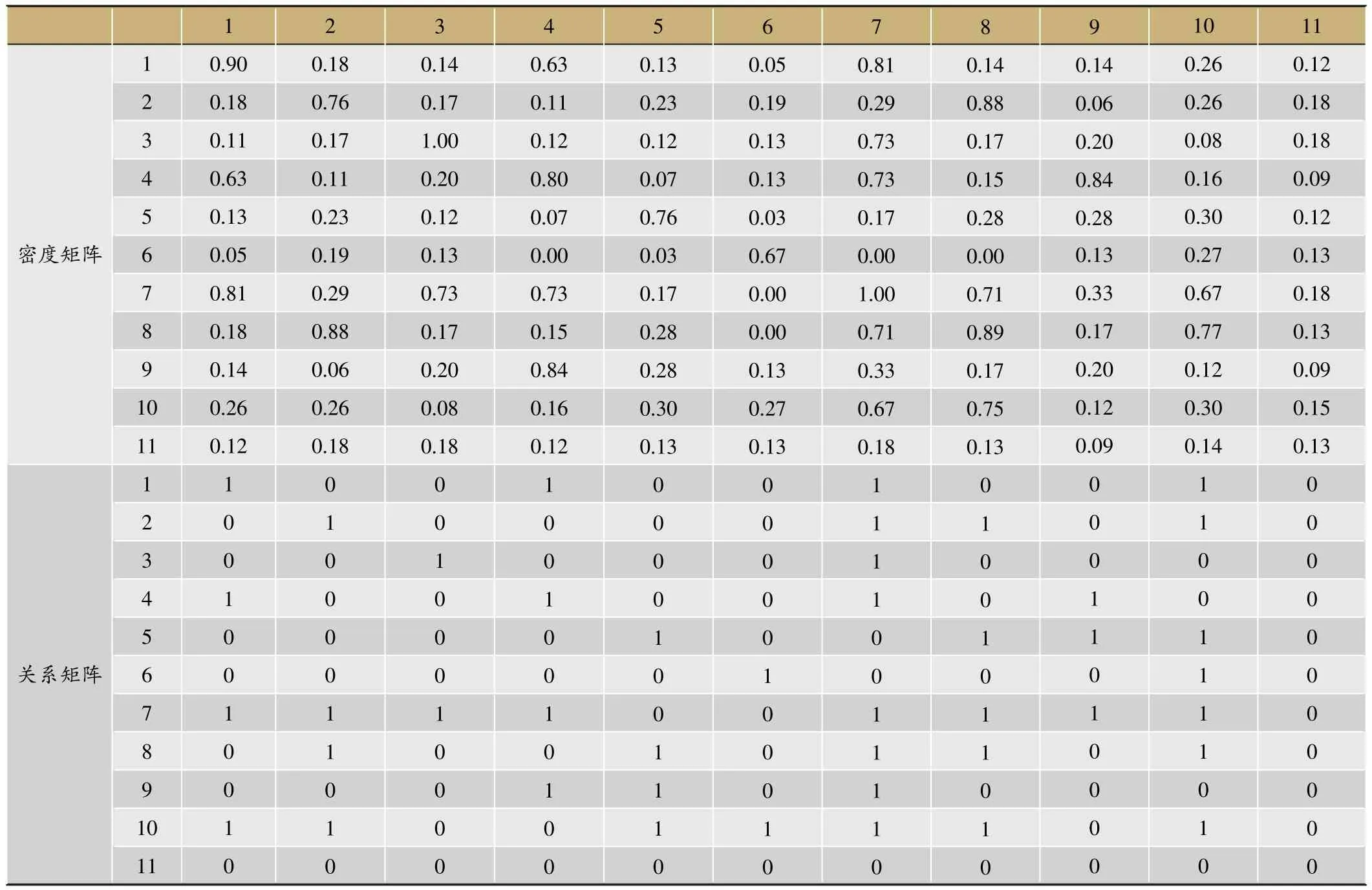
表6 发作期初始密度矩阵及关系矩阵

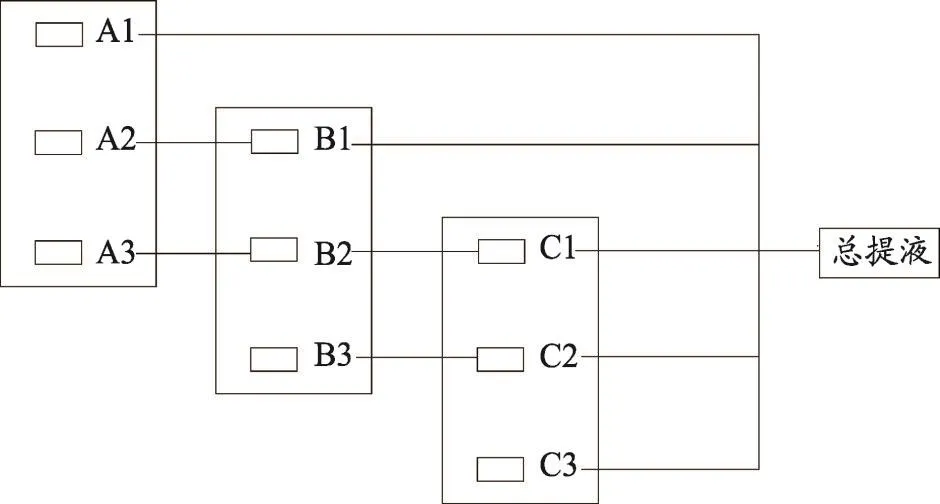
图3 发作期指标子群间结构关系图

对于一个由众多指标节点构成的复杂网络，如果要进一步挖掘指标节点间隐含的结构关系，就需要利用社会网络理论的方法，对所有的指标进行重排，将复杂网络划分为多个“指标子群”，再对“指标子群”进行凝聚，形成较大规模的“指标群”。这种“先划分再凝聚”的思想，实现了复杂网络在产生指标群后，进一步对指标群间关系进行了深入的研究和探讨。

可供选择的社会网络结构划分方法种类繁多，每种方法研究的角度不同，适用范围不同，存在的局限性不同。因此需要对社会网络结构关系划分方法的局限性及关系进行比较研究，选出最优的方法，用于指标节点间结构关系问题的探讨。Tabu搜索算法既可以人为提前设定群数，也可以实现“先划分再凝聚”的思想，完成指标成群以及群间关系的研究工作。

医学上存在众多中医症状指标，中医诊断更多的是大夫或专家根据这些指标的表现，判断患者的状况。本文借助社会网络分析理论，用Tabu搜索算法客观的研究不同症状指标的组合，以及这些症状指标间关系，为中医指标间结构关系的测度提供一种方法指导和技术支持。

本文通过有中心结构和无中心结构的指标网络结构的仿真实验，验证Tabu搜索算法在不同类型网络结构的划分和测度效果。研究表明，该算法较为准确的实现指标节点网络结构的划分，反映网络中不同指标的“凝聚”情况，同时又可以定量测度指标群间的关系。真实世界的网络均由仿真实验中若干个有中心和无中心的网络结构组成，因此，在一定程度上，Tabu搜索算法可以推广到规模较大或网络结构更复杂的指标间关系的测度问题。但当网络规模增加或结构关系复杂度提升到何种程度时，Tabu搜索算法对指标间关系测度效果会存在显著差异，有待进一步研究。