半导体异质结中场驱动下的散粒噪声特性

程永喜，任全年，景银兰，李淑青

(太原工业学院 理学系,山西 太原 030008)

0 引言

半导体低维量子结构中因其存在量子效应而表现出许多独特的光学和电学性能,一直是凝聚态物理研究的热点之一。随着分子束外延技术(MBA)和激光烧蚀沉淀技术等实验条件和工业技术的发展,不同的半导体低维量子结构在实验上被制备[1]。这为实验研究半导体异质结中低维量子结构的相关特性，如:自旋调控[2]、量子输运[3-4]等提供了平台。

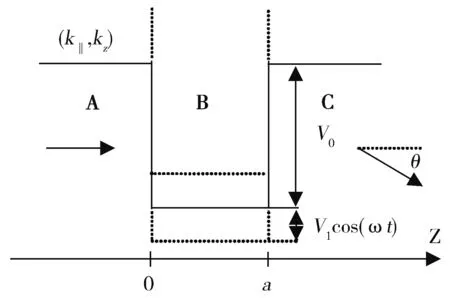
Fig.1 Quantum well driven by a external field图1 外场驱动的量子阱

随着自旋电子学的发展,低维量子结构中自旋相关的物理现象得到了极大关注。人们在自旋注入、自旋控制以及自旋输运等领域开展了大量的实验和理论研究。在量子点、超晶格等低维量子结构中已观测到光子辅助的量子共振隧穿[5-6]。利用半导体异质结中的自旋-轨道耦合,理论预言了非磁半导体异质结中光子辅助自旋相关的量子输运[4]。物理量的随机涨落称为噪声,是量子系统的内在属性。理论和实验上对光量子噪声的研究可以追溯到20世纪60年代。近年来,半导体异质结中散粒噪声的研究逐渐成为研究的热点。散粒噪声作为一种非平衡态噪声,与载流子电荷的离散性有关,作为量子光学的测量手段被广泛应用于量子理论的光子统计中[7-8]。散粒噪声目前已成为表征和探测量子体系性质的重要手段之一[9-10]。近来,针对介观体系的散粒噪声谱的特性,理论和实验上开展了一系列研究。Boylo研究了金属-绝缘体-超导异质结体系中光子辅助的散粒噪声特性。该体系中散粒噪声的强度对外加振荡场的幅度和频率都有较强的依赖[11]。特别是随着量子点设备在实验上的成功制备,为研究散粒噪声谱的特性提供了理想平台。Zhao等人研究了自旋极化量子点系统中不同外磁场调控下的散粒噪声谱特性。随着旋转磁场向振荡磁场的转变,散粒噪声谱会发生从次泊松型向超泊松型的增强[12]。Chen等人研究了与Majorana费米子耦合的量子点体系中的散粒噪声谱的特性,给出了不同耦合强度下散粒噪声谱的变化趋势,为实验上探测Majorana费米子提供了理论指导[13]。Zhang等人还探讨了与Majorana费米子耦合的环形碳纳米管中散粒噪声的特性,分析了Majorana费米子调制下散粒噪声的振荡行为[14]。此外,半导体异质结中的自旋相关的量子噪声特性将有助于量子输运的相关研究以及量子纠缠态的检测,并对实验上制备相应的量子光学器件具有重要的理论指导意义。半导体异质结中Rashba自旋-轨道耦合作用下自旋依赖的散粒噪声特性已经开展相关理论研究[15-16]。本文将考虑外加振荡场条件下,研究磁性半导体异质结中Dresselhaus自旋-轨道耦合作用下自旋相关的量子噪声特性,首先给出了半导体量子阱中磁化强度依赖的束缚态能级结构,并进一步探讨了外场-电子相互作用对散粒噪声的影响,分析了自旋-轨道耦合作用对散粒噪声的调控机制。

1 模型和Floquet理论

(1)

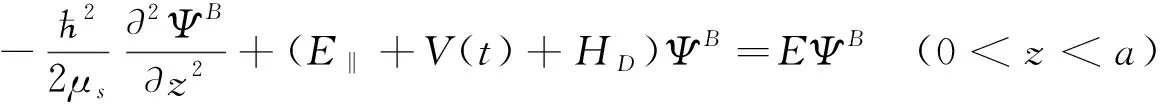
(2)

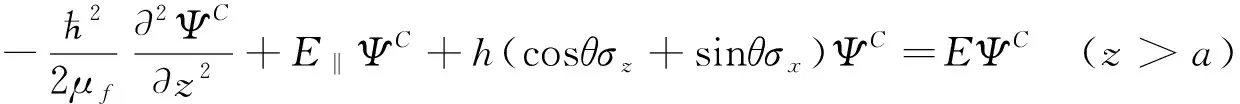
(3)

该模型中比较关注的是中间区域B中所加的外场,定义所加外场随时间周期性变化,即V(t)=-V0+V1cosωt,其中V0是势阱的深度。Floquet理论是求解含时周期场的薛定谔方程的最有效方法之一。利用无限维的时间依赖Floquet哈密顿量HF代替Hilbert空间中有限维的时间依赖的哈密顿量,来描述自旋体系的时间演化行为。所以,对于我们研究的模型,Floquet理论是比较有效的方法。该方法还可以应用于原子和分子谱学中,且在强相互作用的场中,能够得到与量子理论一致的结果。

对于量子系统中的含时哈密顿量H(r,t)=H(r,t+τ),其中τ是周期势的周期。量子系统的薛定谔方程可表示为:

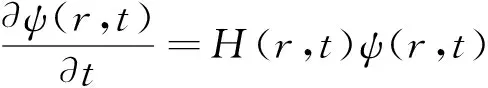
(4)

其中哈密顿量可表示为H(r,t)=H0(r)+Hext(t),Hext(t)=Hext(t+τ).

假设哈密顿量H0(r)的本征函数构成完备集,薛定谔方程的波函数ψ(r,t)可表示为ψ(r,t)=φ(r,t)e-iεf t/ћ,其中εf为Floquet准能量,φ(r,t)=φ(r,t+τ)是周期函数,而且是平方可积的。把波函数代入薛定谔方程(4)得到φ(r,t)满足的方程:

(5)

为了给出入射电子自旋为↑时,磁性半导体异质结中的光子辅助输运特性,利用以上Floquet理论和分离变量法可以分别得到三个区域的波函数:

ћ)

(6)

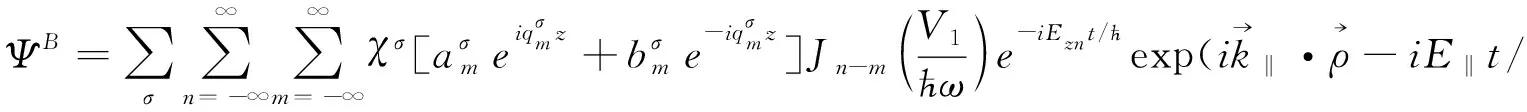
(7)

(8)

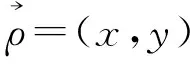
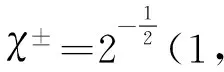
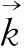
(9)

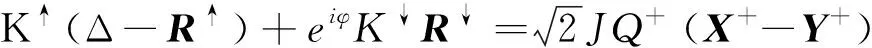
(10)

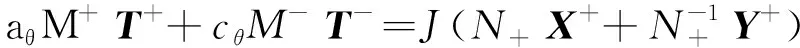
(11)

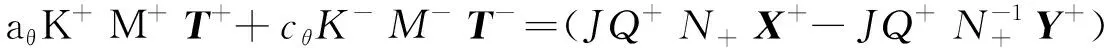
(12)

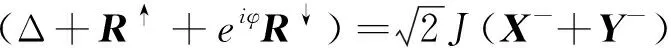
(13)

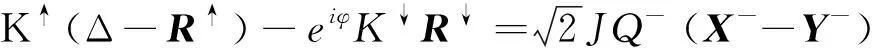
(14)

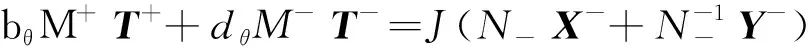
(15)

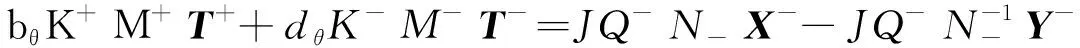
(16)

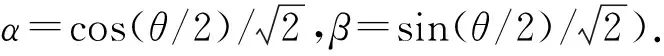
(17)

当入射电子自旋为↓时,A区的波函数应改写为

ћ)

(18)

重复上面的计算程序,可以得到与(9)-(16)式类似的一组矩阵方程,从而可以得到入射电子自旋为↓时的透射率

(19)

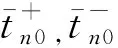
2 数值结果与讨论

首先,我们令V(t)=-V0通过波函数在边界处的连续条件,求得自旋-轨道耦合作用下束缚态能级的相关特性。图2给出了不同自旋劈裂能下，自旋向上和自旋向下的束缚态能级随阱宽的变化,所用的参数为V0=300 meV,K‖=106cm-1,对于半导体GaSbγ1=187 eV,非磁半导体μs=0.082 me,对于铁磁体半导体μf=0.056 me,me是裸电子的质量。自旋-轨道耦合作用使得势阱内的束缚态能级发生了劈裂,劈裂的束缚态能级随着半导体阱宽a的增大逐渐减小,且劈裂的能级的差值逐渐增大(图2(a)所示)。系统中交换劈裂能h的出现使得势阱内两个束缚态能级之间的劈裂宽度进一步展宽。如图2(b)所示,当交换劈裂能h出现后,同一阱宽a下自旋向上的束缚态能级会增大;而自旋向下的束缚态能级则会减小。并且,我们进一步发现势阱宽度a越小,交换劈裂能h对束缚态能级的影响越大。在阱宽a较小(a≤54Å)的条件下,不同交换劈裂能h下束缚态能级Eb有较大的差值,但随着阱宽a的增大(a≥54Å),交换劈裂能h对束缚态能级的影响逐渐减小(如图2(b)所示)。因此,交换劈裂能对束缚态能级的影响可以等效于势阱的有效宽度。

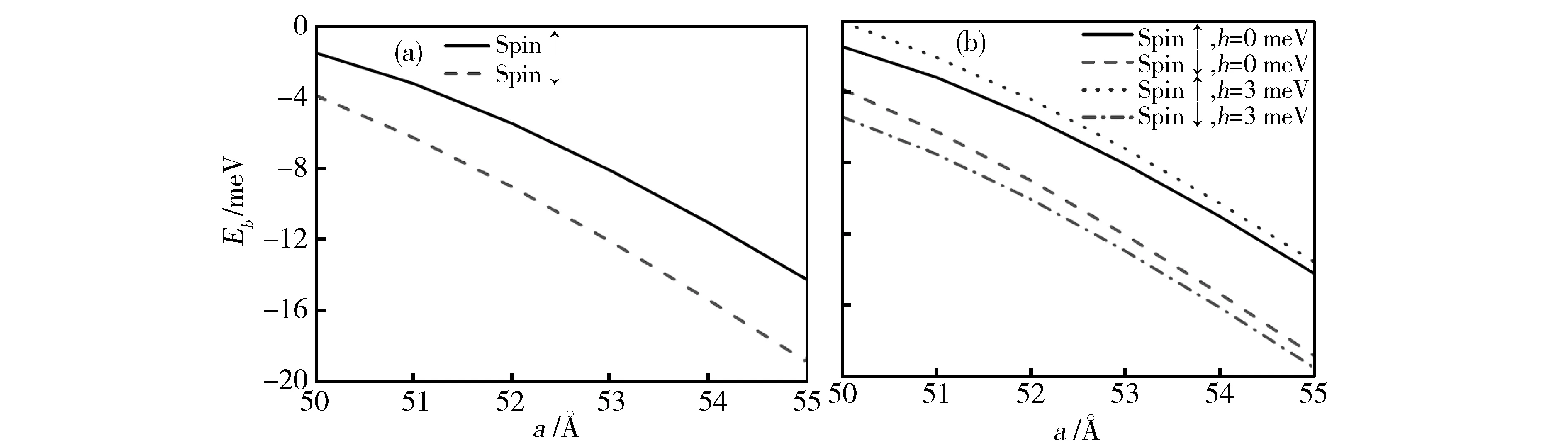
Fig.2 Bound level as a function of the width of potential well图2 束缚态能级随势阱宽度的变化

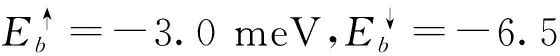
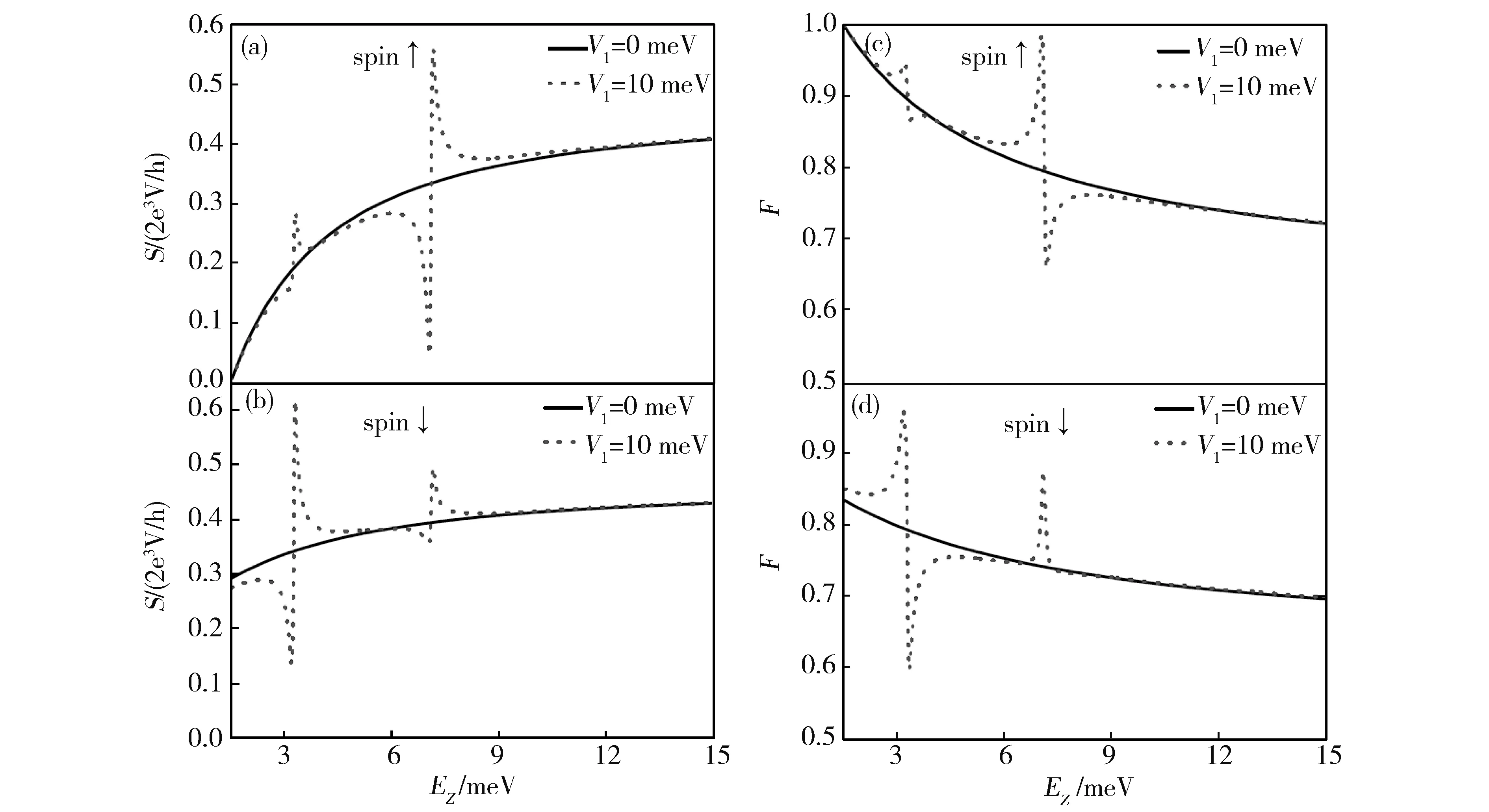
Fig.3 Shot noise spectrum and Fano factor as a function of the magnetization Ez图3 散粒噪声谱和Fano因子随入射不同自旋电子的入射能量Ez的变

由自旋-轨道耦合作用所导致的劈裂的束缚态能级会对散粒噪声产生较大的影响,这对研究自旋相关的量子输运现象提供了有力手段。图4给出了不同的入射方向下,散粒噪声谱密度随交换劈裂能h的变化。我们发现,散粒噪声谱对交换劈裂能h具有较强的依赖关系。且入射不同自旋的电子时,散粒噪声S对交换劈裂能h的依赖关系也不同。对于入射自旋向上的电子,散粒噪声S随着交换劈裂能h的增加而减小;但对于入射自旋向下的电子,散粒噪声S随着交换劈裂能h的增加而增大。这是由于磁化强度的增大对势阱中电子的自旋翻转有抑制作用,导致散粒噪声对入射不同自旋电子有不同的依赖行为。

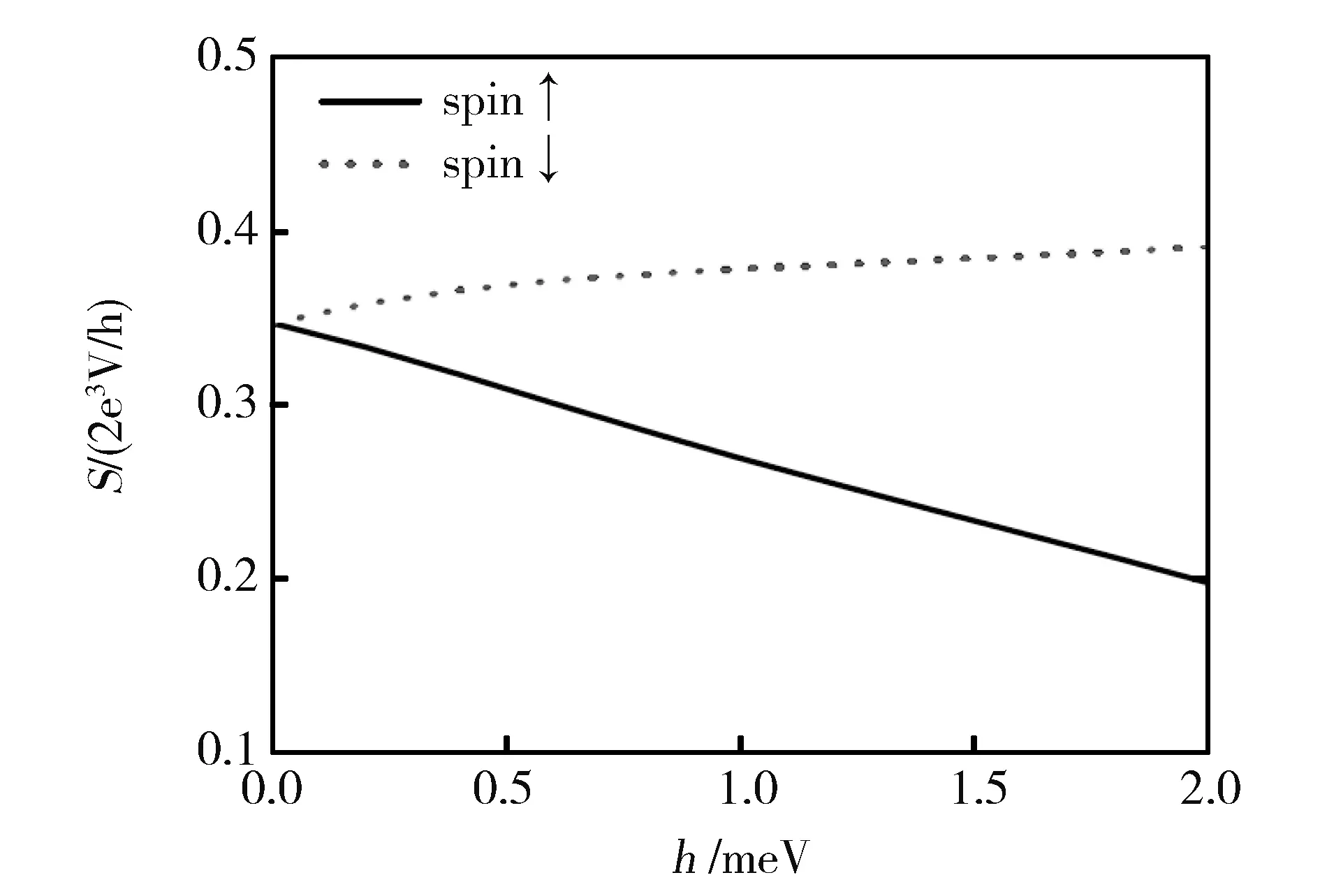
Fig.4 Shot noise spectrum as a function of the magnetization h图4 入射不同自旋电子的散粒噪声谱随交换劈裂能h的变化

为进一步研究散粒噪声对磁化夹角θ的依赖,图5(a)和(b)给出了外场V1=10 meV不同的交换劈裂能h下,入射电子自旋分别为上和下时,散粒噪声随着磁化夹角θ由0增加到π的过程中的变化趋势。当入射电子自旋为上时,对于较小交换劈裂能h=0.5 meV,散粒噪声谱变化比较平滑,在θ=1.6 rad处成对称趋势;当交换劈裂能增大到h=1.0 meV,散粒噪声谱会增强,并且产生双峰的结构;当交换劈裂能增大到h=1.5 meV,散粒噪声谱在夹角θ=1.3 rad和θ=2.3 rad处出现了两个不同高度的劈裂峰;对于较强的交换劈裂能h=2.0 meV,劈裂的双峰的高度都会减小,且劈裂的双峰的位置会向右移动。在交换劈裂能逐渐增加的过程中,散粒噪声谱逐渐由对称变成了非对称,且角度较大(θ=2.3 rad)处的劈裂峰较高(图5(a)所示)。

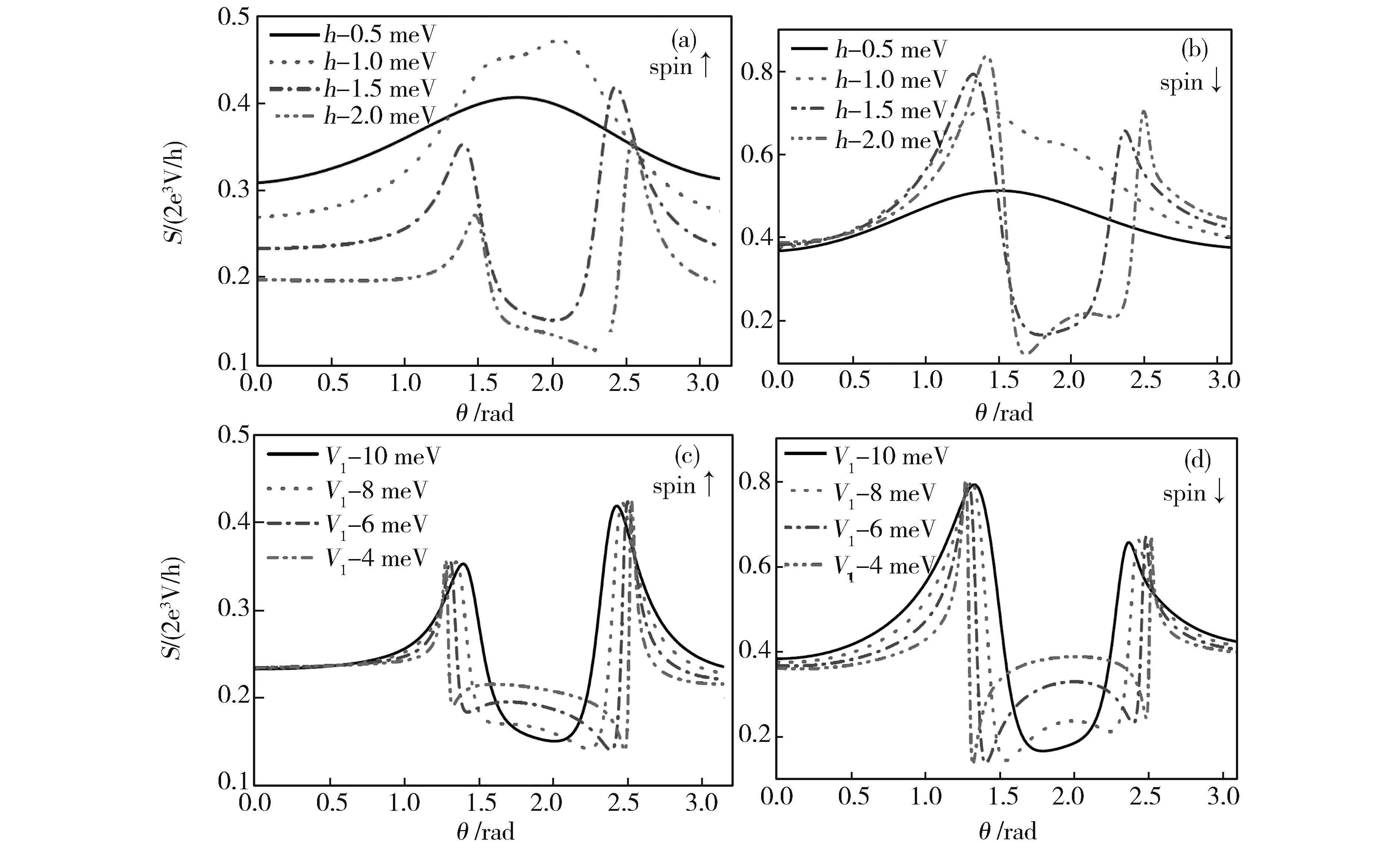
Fig.5 Shot noise spectrum as a function of the angle θ for different magnetizations applied field 图5 不同交换劈裂能和外场下散粒噪声谱密度随夹角θ的变化

当入射电子自旋为下时,散粒噪声谱的变化趋势与入射电子自旋为上产生较大不同。当交换劈裂能h=0.5 meV时,散粒噪声谱的变化趋势与入射电子自旋为上的变化趋势相类似,同样存在比较平滑的变化,且会在θ=1.6 rad处成对称趋势;但当散粒噪声谱出现劈裂的双峰之后(h>1.5 meV),随着交换劈裂能的增加,劈裂的双峰的高度会增大,且角度较小(θ=1.3 rad)处的劈裂峰较高(图5(b)所示)。由此我们发现,随着交换劈裂能的增加,散粒噪声谱曲线逐渐由对称转换为非对称。在出现双峰后,不同取向的自旋电子在穿过半导体量子阱时散粒噪声是不同的。当入射电子自旋为上时,劈裂的噪声谱峰随着交换劈裂能的增加逐渐减小,当入射电子自旋为下时,劈裂的噪声谱峰随着交换劈裂能的增加逐渐增大。进而,我们预测对于多通道电子输运情形,交换劈裂能和磁化夹角的变化同样会使得散粒噪声发生较大的变化。

图5(c)和(d)给出了交换劈裂能h=1.5 meV不同外场下,入射电子自旋分别为上和下时,散粒噪声随着磁化夹角θ由0增加到π的过程中的变化趋势。发现入射电子自旋方向为上和下的噪声谱的双峰结构在不同的外场下都保持不变,但双峰的位置和高度会受到外场的调制。随着外场V1=10 meV向V1=4 meV减弱过程中,入射电子自旋方向为上和下的散粒噪声谱的双峰会逐渐向相反的方向移动,且双峰之间的距离会逐渐加宽。谷底的散粒噪声谱的高度会随着外场V1的减弱而增强。这为从外场调控的角度观测散粒噪声谱的双峰结构的变化提供了可能。

3 结论

本文基于有效质量近似和Floquet理论,研究了磁性半导体/半导体/磁性半导体异质结在外加振荡场作用下散粒噪声的相关特性。势阱中的自旋-轨道相互作用不仅使自旋发生翻转,而且使束缚态能级发生劈裂,势阱两边的磁化强度对阱中束缚态能级具有调制作用。在低频极限下,不同取向的自旋电子在穿过半导体量子阱时散粒噪声是不同的。散粒噪声谱会随着交换劈裂能的增加逐渐由对称转换为非对称,特别是当出现劈裂的双峰之后,入射自旋方向为上的电子的噪声谱峰的高度会随着交换劈裂能的增加而减小;入射自旋方向为下的电子的噪声谱峰的高度会随着交换劈裂能的增加而增大。随着外场减弱散粒噪声谱的双峰会逐渐向相反的方向移动,双峰之间的距离会逐渐加宽,且谷底的散粒噪声谱的高度会随着外场的减弱而增强。这些结果对于磁性半导体异质结材料在量子器件及其输运方面有较大的应用价值。