高分一号卫星影像谐波模型模拟方法研究

廖 戬， 顾行发， 占玉林， 张雅洲， 任芯雨， 师帅一

(1.中国科学院遥感与数字地球研究所,北京 100094； 2.中国科学院大学,北京 100049)

0 引言

遥感监测技术正广泛地应用于农业调查、林业调查、城市管理规划、基础地理数据库更新、土地退化和荒漠化监测、海洋和内陆水体监测、沿海区域环境监测、湿地监管、自然灾害监测以及军事侦察等社会经济各领域[1]。一方面，遥感技术应用推动着这些领域朝着更加深入的方向发展； 另一方面，领域应用的发展对监测产品的时空分辨率提出了更高的要求。因此，获取干净(无云、雾、雪及云阴影覆盖)的高时空分辨率系列影像数据至关重要。

然而，限于目前卫星技术的发展水平，卫星影像时间分辨率与空间分辨率之间存在难以调和的矛盾，加上云、雾、雪及云阴影等因素的影响，要获取干净的高时空分辨率序列影像非常困难。本文以高分一号(GF-1)卫星数据为例，在中国资源卫星应用中心网站上，设定时间范围为2013年4月26日—2016年4月1日，区域范围为北京市，能够查询到748景空间分辨率为16 m 的GF-1 WFV传感器影像； 然而，去除不能完整覆盖北京市及云、雾等遮挡严重的影像后，仅剩下68景，符合要求的影像占比不到10%。因此，研究一种影像模拟方法极具实用价值。

目前，学者们已经提出了一些影像模拟方法，其中一类是基于融合的方法，利用单一准则(例如最小红光波段)或多准则选择云量最小的“最佳”观测[2-9]，将高时间分辨率低空间分辨率影像融合到高空间分辨率低时间分辨率卫星影像中，从而产生模拟影像。例如Hansen等[2]利用MODIS反演的森林覆盖产品校正缺少高时间分辨率数据的Landsat影像，实现了对刚果河森林的变化监测； Griffiths等[3]将影像获取日期、邻近像元到目标像元的距离考虑到影像模拟模型中，然后参照MODIS数据进行调整，以保证模拟影像的辐射一致性。另一类则基于像元解混技术，从低空间分辨率影像推算出高空间分辨率像元反射率，进而生成模拟影像。邬明权等[10]利用MODIS和Landsat影像数据结合土地利用分类数据综合对比了基于LORENZO模型、LIU模型和统计模型等利用像元解混技术的模拟方法。这些方法虽然取得了较好的效果，但是需要多源数据(即获取目标日期前后2景干净的高空间分辨率卫星影像以及若干低空间分辨率卫星影像)，而且高空间分辨率影像的时间间隔直接影响到模拟影像的精度。本文将研究一种基于傅里叶谐波模型的能够利用单一数据源时间序列影像的模拟方法，旨在有效提高GF-1卫星影像时间分辨率。

1 研究区概况及数据源

1.1 研究区概况

本文以北京市为研究区。北京市地处华北平原与太行山脉以及燕山山脉的交接处，地理范围为E115°25′～117°30′，N39°26′～41°03′； 区内植被、人工建筑物、水体等地物丰富，区块分布明显，极具代表性，利于验证模型的正确性与适用性。此外，北京市是我国政治、文化中心，科技创新中心和国际交往中心，对该区域进行研究具有典型的应用价值和意义。

1.2 数据源及其预处理

首先对2013年4月26日—2016年4月1日间所获取到的GF-1卫星WFV影像数据进行初步筛选，剔除对北京市地区覆盖不全和明显有云、雾覆盖的影像，得到68景影像； 接着使用ENVI5.3软件对初步筛选出的影像分别进行辐射校正、大气校正、几何纠正和裁剪等预处理，裁剪后的数据只覆盖北京市地区，小部分裁剪后的影像仍然存在少量云、雾覆盖的情况，这部分影像也被剔除； 然后选定1景影像作为基准影像进行配准，配准后所有影像的空间分辨率均重采样到16 m； 再次裁剪影像，使所有影像具有相同的幅宽和起始地理坐标，最终得到了46景实验影像。

2 基于谐波模型的地表反射率模型

基于谐波模型的地表反射率模型由傅里叶谐波模型[11-12]和长期趋势分量组成，根据模型复杂度可细分为简单、高级和完全3种模型。

简单模型只有4个参数，第一个参数a0,i用于模拟第i波段反射率总体情况，表示该波段的基准值； 第二、三个参数a1,i和b1,i用于建模，表示第i波段由于物候与太阳高度角变化引起的年内变化； 最后一个参数c1,i用于评估第i波段的长期趋势，这个参数十分重要，因为它可以模拟地表本身具有的一种持久性的渐变过程。简单模型公式为

(1)

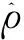
简单模型已成功运用于美国和新英格兰土地覆盖连续变化检测与分类[13]，在某些情况下表现良好[14]，但在不符合简单模型单峰变化(模型曲线在一个周期内只有1个峰值)的地区效果不佳。

高级模型在简单模型的基础上引入a2,i和b2,i模拟地表的双峰(一个周期内有2个峰值)变化，即

(2)

式中a2,i和b2,i为第i波段年内双峰变化系数。

完全模型则是在还有更多可用观测数据的情况下，在高级模型的基础上引入a3,i和b3,i，模拟更加复杂的地表三峰变化(一个周期内有3个峰值)，使模型更加符合地表反射率变化，即

(3)

式中a3,i和b3,i为第i波段年内三峰变化系数。

Verbesselt等[15]基于卫星时间序列影像，将一种类似的模型成功运用于森林扰动近实时检测。

图1(反射率已扩大104倍)显示了运用3种不同的地表反射率模型对北京市GF-1卫星影像波段1中心像元的拟合情况。从图1可以看出，简单模型(红色)只能模拟地表年内随着时间变化产生的简单变化，而高级模型(绿色)与完全模型(蓝色)则表现了影像数据随时间产生的复杂变化。理论上，越复杂的模型，精度越高。对于高空间分辨率影像中每个波段的每个像元，均需要拟合一个谐波模型。研究表明[13]，为了使模型评估结果具有准确性和稳定性，观测数至少是模型系数个数的3倍。因此，如果观测数为12～18个，只能使用简单模型模拟地表反射率； 如果观测数在18～24个之间，则可使用高级模型模拟地表反射率； 如果观测数≥24，就可使用完全模型模拟地表反射率。针对不同的观测数可以使用的模型如表1所示。

图1 简单、高级、完全3种模型拟合Fig.1 Simple, advanced and full model regression表1 观测数与模型选择Tab.1 Number of observation and model selection

观测数模型0置为背景值1置为该观测值2～11加权平均12～17简单模型18～23高级模型≥24完全模型

由于本研究获取了46景无云、雾、雪及云阴影覆盖的遥感影像，使用其中4景作为验证影像，还剩余42景作为建模输入，故可以采用完全模型对地表反射率进行模拟。

3 实验结果与分析

3.1 实验过程

本研究包含2个实验，实验一的目的是以完全模型为例探究谐波模型模拟方法的精度与稳定性，实验二则是研究简单、高级和完全模型的适用性。

实验一的步骤包括模型生成与影像模拟。①以42景干净的GF-1 WFV影像作为输入数据，通过最小二乘法为每个波段每个像元解算出一个谐波地表反射率模型； ②指定2013年4月26日—2016年4月1日期间任意日期，并将该日期转换为儒略日作为步骤①生成的地表反射率模型的输入，估算单个像元的地表反射率，对模型覆盖范围内每个波段每个像元进行计算，即可模拟1景指定日期的GF-1卫星影像。为了评估基于谐波模型的影像模拟方法的精度与稳定性，本研究选用了简单的线性插值影像模拟方法与本文方法进行对比，即选取距离目标影像最近的前后2个时期的高空间分辨率影像，通过距离加权插值方法模拟目标影像。实验输入与精度验证影像参数设置详见表2(以影像获取日期为文件名)。

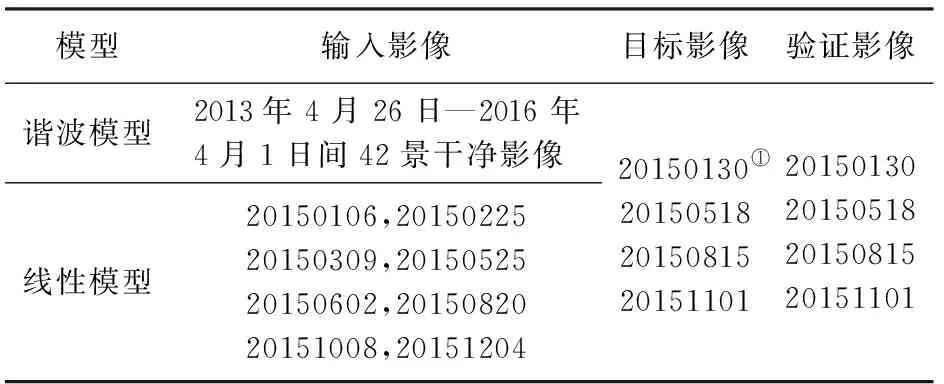
表2 实验一的输入与精度验证影像参数设置Tab.2 Experiment-1 input and precision validation parameters

①以影像获取日期为文件名。

实验二分为5个小实验(分别编号为A，B，C，D，E)，其基本步骤与实验一相同； 不同的是每个小实验的输入数据量不同，即从42景GF-1 WFV干净影像中选择不同景数影像分别实验，选择的模拟模型分别是简单、高级和完全模型中的一种，不再使用线性模型； 目标影像和验证影像均为20150130，实验输入影像与模型选择如表3所示。

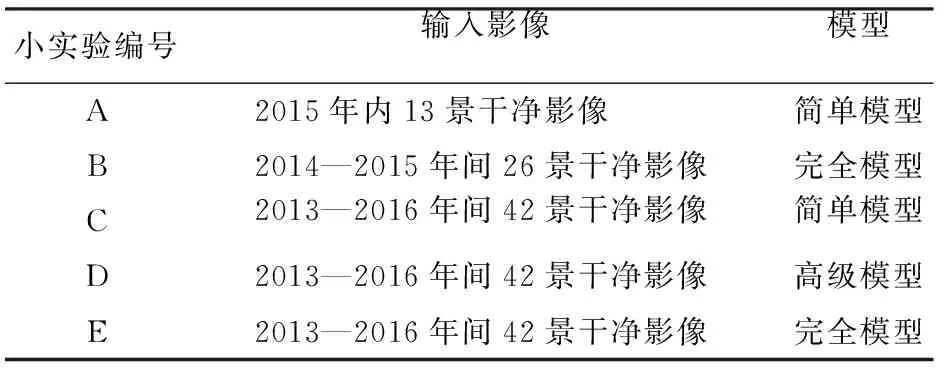
表3 实验二的输入设置与模型选择Tab.3 Experiment-2 input and model selection

3.2 精度评定

为了评估模拟算法的精度，首先从视觉上对几组模拟影像与真实影像进行定性比较； 然后计算真实影像与模拟影像之间的差值影像，并对差值影像进行统计，从差值影像各波段直方图、最小值、最大值、平均值、标准差以及均方根误差(root mean square error，RMSE)几个维度对算法的影像模拟精度进行定量估计。

3.2.1 视觉对比

评估模拟影像准确性最简单的办法就是将模拟影像与同一日期真实影像进行对比。本研究模拟的4景GF-1影像，分属2015年的4个季节，都能获取到真实的覆盖北京地区的GF-1影像，能够评估算法在时间和空间上的适用性(图2)。

(a) 20150130谐波模拟影像 (b) 20150130线性插值模拟影像(c) 20150130真实影像

(d) 20150518谐波模拟影像 (e) 20150518线性插值模拟影像(f) 20150518 真实影像

(g) 20150815谐波模拟影像 (h) 20150815线性插值模拟影像(i) 20150815真实影像

(j) 20151101谐波模拟影像 (k) 20151101线性插值模拟影像(l) 20151101 真实影像

图2基于谐波模型、线性插值模型生成的模拟影像与真实影像(B4(R),B3(G),B2(B)假彩色合成影像)

Fig.2Syntheticimagesgeneratedbyharmonicmodelandlinearinterpolationmodelandrealimages

在视觉上，4景模拟影像与真实影像较难区分(图2)，这说明算法具有一定的估算能力。基于谐波模型模拟的2015年1月30日的影像(图2(a))和对应的真实影像(图2(c))亮度差异较小，而基于线性插值模拟的影像(图2(b))的亮度偏暗，与真实影像(图2(c))亮度差异较大； 2015年11月1日线性插值模拟影像(图2(k))出现了明显的偏色，而谐波模型模拟影像(图2(j))与真实影像(图2(l))仍然保持较高的相似度。这主要是因为这2组实验中，线性插值模型输入影像的时间间隔较长，直接影响了模拟精度； 而谐波模型由于综合考虑了地表反射率的年内变化趋势，因而具有更高的精度与稳定性。

截取2015年1月30日模拟影像与真实影像左上角400像元×400像元做进一步对比(图3)。可以明显观察到，基于谐波模型生成的模拟影像(图3(a))的总体色调接近真实影像(图3(c))； 在图3中标记出的“1”处与“2”处，基于谐波模型生成的模拟影像与真实影像更相似。

(a) 谐波模型模拟影像 (b) 线性插值模拟影像 (c) 真实影像

图32015年1月30日模拟影像与真实影像

Fig.3Syntheticimagesandrealimagesat20150130

3.2.2 定量评估

为了定量评估模拟高空间分辨率影像的精度，采用模拟影像与真实影像之间的差值影像基本统计量及RMSE作为评估指标。以2015年1月30日模拟影像为例，计算其与真实影像差值影像并统计，得到差值影像直方图和基本统计量(图4和表4)。基于谐波模型的模拟影像与真实影像的差值影像中，差值处于-0.03～0.03之间的像元占比为90%以上(图4(a))，差值影像的标准差为0.02左右，模拟影像与真实影像间RMSE保持在0.02～0.05之间(表4)，这表明模拟影像与真实影像差值较小，波动不大。

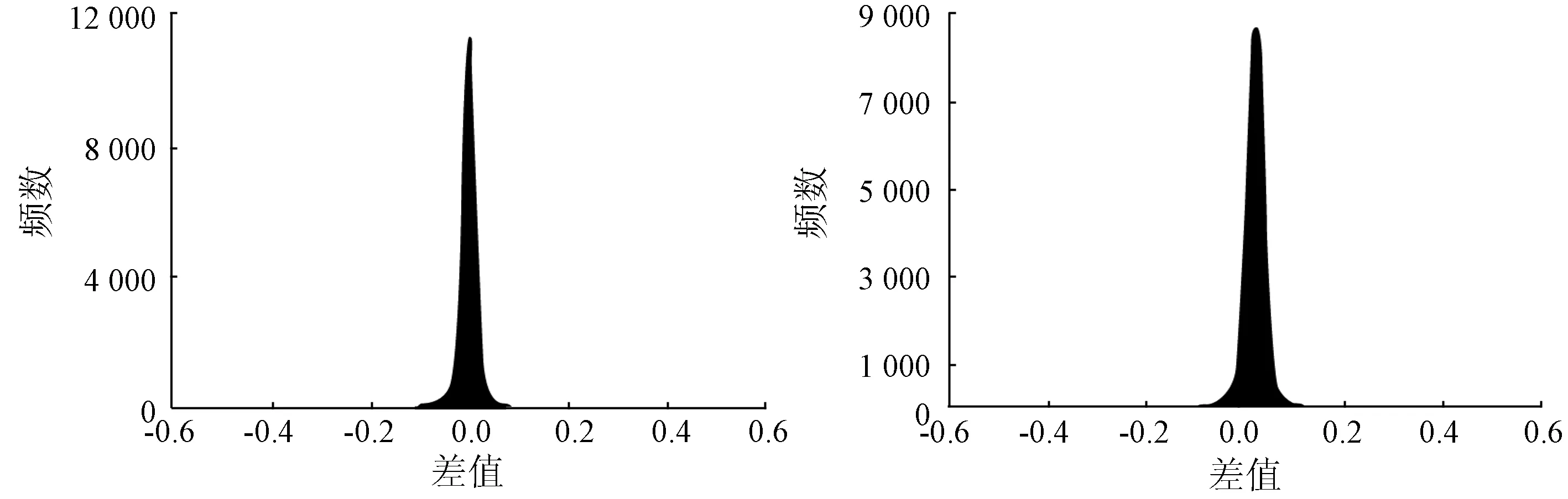
(a) 谐波模型 (b) 线性模型

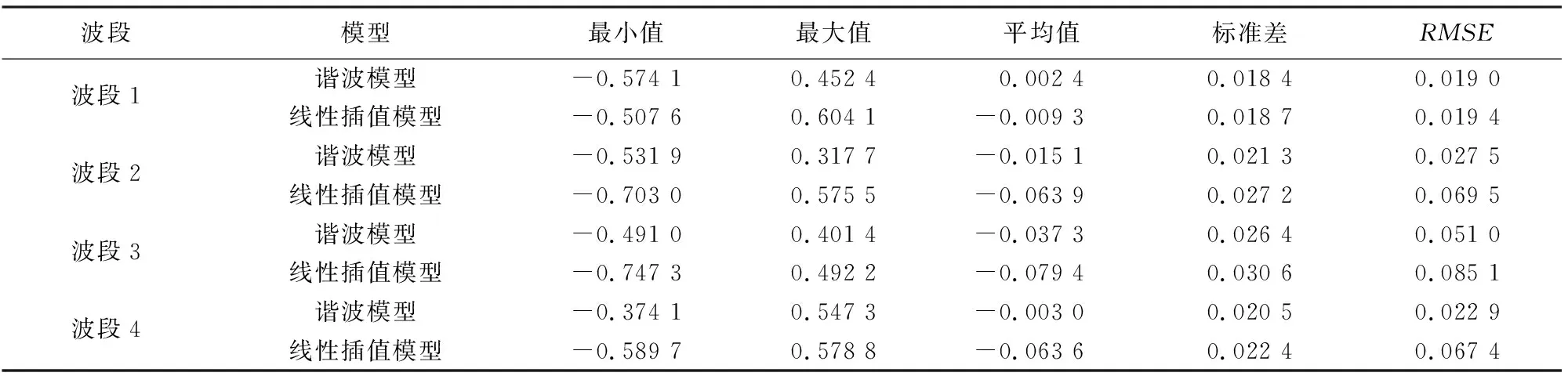
图4 模拟影像与真实影像波段1差值影像直方图Fig.4 Histograms of difference image between synthetic image and real images表4 模拟影像与真实影像之间差值影像统计Tab.4 Statistics of difference between synthetic images and real images

另一方面，将基于谐波模型的模拟影像与真实影像之间的差值影像与基于线性插值模型的模拟影像与真实影像之间的差值影像统计量进行对比，前者直方图(图4(a))比后者直方图(图4(b))更集中于0附近，后者90%以上像元的差值处于-0.02～0.07之间，前者基本统计量的所有指标均优于后者(表4)； 且后者差值的平均值为前者的数倍，各波段标准差均大于前者，除波段1的RMSE仅比前者大0.004外，其余波段RMSE均为前者的2～3倍(表4)，这表明基于谐波模型的影像模拟方法具有较高的精度和稳定性。

3.3 谐波模型适用性研究

实验二的结果如表5和表6所示，对比实验A和C(简单模型，数据量不同)以及实验B和E(完全模型，数据量不同)。

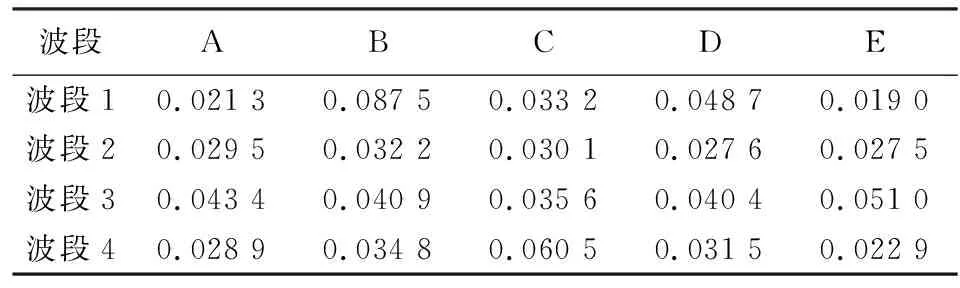
表5 2015年1月30日模拟影像与真实影像之间的RMSETab.5 RMSE between synthetic image and real image at 20150130

表5中融合影像与真实影像之间的RMSE结果表明，当数据量增大时，简单模型由于过拟合导致精度下降(C)，而完全模型精度则随着数据量增大而增高(E)。

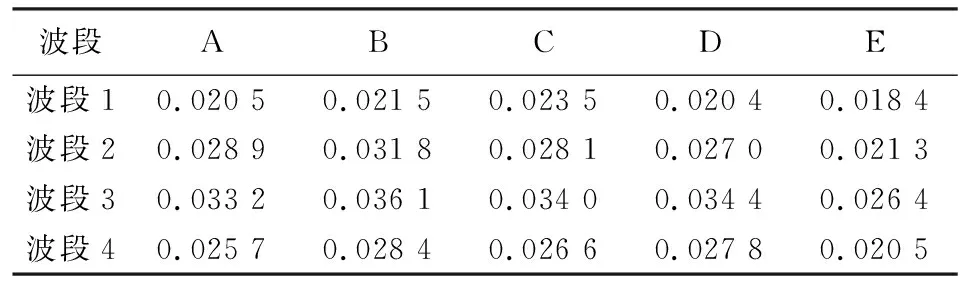
表6 2015年1月30日模拟影像与真实影像差值标准差Tab.6 Standard deviation of difference between synthetic image and real image at 20150130

表6所示差值影像标准差表明，当数据量较大时，简单模型出现了过拟合的情况，稳定性降低； 而完全模型则没有出现过拟合，数据量增大时，模型稳定性增加。对比实验C，D和E(模型依次为简单、高级、完全，数据量相同)，表5与表6中的数据均表明，融合准确性及稳定性与模型的复杂度并不是正相关的，例如完全模型(表5，E)第3波段准确性低于高级模型(表5，D)，其他波段高于高级模型； 高级模型(表6，D)模拟影像第4波段稳定性低于存在过拟合问题的简单模型(表6，C)，而第1波段高于简单模型(表6，C)。可见，每一种模型的准确性和稳定度是模型复杂度、输入影像数量和影像波段特性综合作用的结果，实际应用中应根据模拟影像精度评定结果确定使用的模型。

4 结论

1)通过使用国产高分一号(GF-1)卫星已有的观测数据和基于谐波的地表反射率模型模拟影像，利用时间序列影像挖掘地表反射率的年内变化，弥补在特定时期内不能获取足够接近目标日期的输入影像造成的精度影响，有效地提高了GF-1卫星影像的时间分辨率，模拟的高分辨率影像具有较高的精度与稳定性。

2)因为谐波地表反射率模型可以模拟季节性的地表反射率变化，模拟影像将不受太阳角度变化的影响。

3)该方法3种模型的准确性和稳定性是由模型复杂度、输入影像数量和影像波段特性综合作用共同决定的，实际应用中应该根据模拟影像精度评定结果确定使用的模型。

基于谐波模型的影像模拟方法应用于GF-1影像虽然取得了较好效果，但是还有许多问题需要深入研究。首先，最小二乘法容易出现过拟合问题，所以需要考虑更稳健的模型解算方法； 其次，模型不能够模拟人为造成的地表突变，限制了该方法在实际生产环境中的应用，需要进一步探索相应的解决方案。