一种改进的ICM遥感影像分割算法

杨 军， 裴剑杰

(1.兰州交通大学电子与信息工程学院,兰州 730070； 2.兰州交通大学测绘与地理信息学院/甘肃省地理国情监测工程实验室,兰州 730070)

0 引言

随着遥感技术的发展，不同传感器获取的遥感影像开始广泛应用于农业、林业、环境监测、城乡规划以及军事侦察等领域[1-4]。为了充分利用遥感影像数据中包含的有用信息，研究人员进行了大量影像分析处理研究，其中影像分割成为该领域的研究热点之一。目前，已有许多理论和技术被用于影像分割，其中马尔科夫随机场(Markov random field, MRF)模型方法融合了局部先验模型和像元的邻域结构信息，在影像分割中得到广泛应用[5-7]。由贝叶斯理论可知，影像分割问题可以把计算已知观测影像标记场的最大后验概率问题转换为等价的吉布斯随机场(Gibbs random field, GRF)能量函数最小化问题[8]。现有的能量函数最小化算法包括全局优化和局部优化2大类，全局优化算法[9]有Metropolis算法、模拟退火算法(simulated annealing, SA)、图割算法(graph cuts, GC)和遗传算法(genetic algorithms, GA)等； 局部优化算法[10]有迭代条件模式(iterated conditional model, ICM)算法、马尔科夫链蒙特卡罗(Markov chain Monte Carlo，MCMC) 算法和神经网络算法等。在能量函数最小化优化的众多算法中，ICM算法是一个经典的局部优化算法，通过在求解后验概率最大化的迭代过程中采取“贪婪”的策略，每次对标记的赋值采取条件概率最大的方式，因而能非常快速地达到能量函数在邻域系统内的极值。与全局优化算法(如SA算法和GA算法)相比，ICM算法所需计算时间较少，收敛速度较快； 但由于后验能量函数具有非凸性，ICM算法很容易收敛到一个局部极值上，无法达到全局最优。此外，传统的ICM算法的优化效果受初始标记点的影响较大，一方面，该算法使用K-means聚类法获取初始标记时只考虑了像元的光谱信息，而忽略了像元邻域的空间信息，当影像存在较大的噪声时，分割后的影像往往会出现许多离散斑块和孤立点； 另一方面，如果没有一个合适的初始标记，优化过程往往会陷于局部最优，而对于维数很高的遥感影像数据来说，全局性的更新优化很难实现。对于这个问题，一种解决方法是先对原始影像进行低通滤波，再用ICM算法将能量函数最小化优化，但这种方式会导致分割影像边缘模糊和纹理细节丢失。

近年来，国内外研究者针对影像分割噪声抑制和分割结果准确性之间的平衡进行了广泛研究，对传统的ICM算法提出了许多改进方法。侯一民等[11]在传统ICM算法的邻域基团势函数基础上，引入了邻域中像元的强度差值以及像元之间的距离因子用于分割。杨红磊等[12]提出了用MRF描述像元的空间相关性，引入邻域分类信息作为像元分类的空间约束。这2种方法虽然都很好地抑制了影像噪声的影响，但是每一次迭代都要重新计算邻域信息，算法复杂度高。谢昭等[13]利用K-近邻思想构建图像邻域系统，通过设置合适的初始类别数，用ICM算法进行聚类，提高了聚类准确性； 该方法虽然弱化了初始标记的影响，但是用于分割时结果仍然具有不确定性。Baumgartner 等[14]提出了一种连续波段融合的影像分割方法，将双边滤波器(bilateral filter, BF)结合遥感影像的上下文信息用于分割，类似于运行一个ICM算法； 该算法几乎可以不用迭代即可达到最终分割状态，但分割精度一般。上述方法中没有一个既能有效抑制分割噪声，又能使分割结果具有较高精度、适合大多数遥感影像分割的算法。针对这些问题，本文将保边去噪效果良好的BF引入到传统的ICM算法中，用于保留遥感影像的地物边缘并去除噪声； 然后采用多阈值最大类间方差法(由日本学者大津(Nobuyuki Otsu)提出的一种自适应阈值确定方法，亦称大津法(Otsu))遍历影像直方图主峰的方式获取分割阈值，进而确定初始分割类别数，获取初始标记； 引入MRF度量空间相关性，并采用航摄影像和多光谱影像数据分别进行实验，以验证本文算法的有效性。

1 经典ICM算法

基于MRF的影像分割中，分割影像常用2个随机场来描述，一个是特征场(或称观测场)，另一个是标记场。特征场以标记场为条件，用标记类别的似然分布函数描述特征数据或特征向量的分布； 标记场则用先验知识描述标记场的局部相关性。影像分割需要将特征场中的数据与标记场中的先验知识概率建立有机的联系，这就需要将先验信息所期望的分割结果与真实观测数据的细节信息进行平衡，而贝叶斯决策理论能够很好地做到这一点[15]。基于MRF的影像分割通常用贝叶斯决策理论中的最大后验概率(maximum a posterior, MAP)准则作为MRF建模的优化准则，这就是经典的MAP-MRF框架[16]，该框架下的影像分割问题的实质即计算影像的最大后验概率。由Markov和Gibbs分布的等价性可知，最大后验概率的求解又可以转化为对最小能量函数的计算，而ICM算法是计算最小能量函数的经典算法。

1.1 MRF影像分割问题

设Y为影像数据所表示的特征场或观测场，y是Y的一个样本； 标记场X为影像分割结果所描述的随机场，x是X的一个样本(即一种分割标记结果)。根据贝叶斯决策理论，可将影像分割问题表示为

(1)

式中：P(X=x|Y=y)为在影像数据Y=y给定的条件下，标记场X=x的后验概率；P(Y=y|X=x)为在给定标记场X=x的条件下，观测场Y=y的联合分布或者似然函数；P(Y=y)为观测场Y=y的联合分布。因为观测场Y=y为影像数据，是一个已知量，所以P(Y=y)不随标记场中任意一个X=x的变化而变化。

如果直接根据式(1)进行影像分割，几乎得不到正确的结果，并且计算过程非常复杂。因此，为了进行贝叶斯框架下的影像分割，还需要给出2个基本假设：

1)假设一(条件独立性)[17]： 假设在给定标记场的一个样本的条件下观测场的每一成分相互独立。

如果要从遥感影像中分割出K种地物，那么标记场中会有K个标记，即标记场中的每一位置可能有K种取值。换言之，观测场的所有观测值将被分为K种成分，于是式(1)可表示为

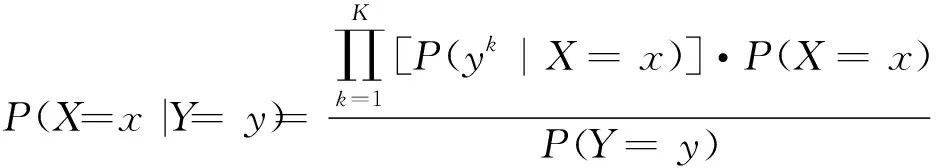
(2)

式中：P(yk|X=x)为在给定标记场X=x的条件下，观测场成分yk的概率分布。

观测场P(Y=y)是已知的影像数据，而标记场P(X=x)可用MRF模型[18]表示。要实现影像分割，只有P(yk|X=x)是一个未知量，所以还需要做进一步假设。

2)假设二(同质区域相同分布)[19]： 假设影像中同一类型的像元服从同一种分布(比如高斯分布、指数分布等)。

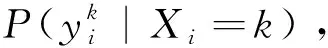
(3)

式中：P(Xi=k|XNi)为标记场的局部先验概率；Ni为位置i的邻域。

1.2 MAP计算

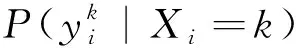
(4)

由于Markov-Gibbs的等价性，可以使用Gibbs分布函数表示MRF邻域系统中的先验概率P(xi|xNi)，从而通过优化能量函数的方法计算式(4)的解。

由Gibbs分布表达式可得，标记场先验概率P(xi|xNi)在Gibbs随机场中的表达式[21]为

(5)

同样，后验概率P(xi|yi)也可以用后验能量函数来表示，即

(6)

在式(5)和(6)中：U(xi|xNi)为影像分割标记问题的先验能量函数；Z为一个称为配分函数的归一化常量；T为温度常量，通常设置为1[18]。

式(5)和(6)式可以进一步转化为

P(xi|xNi)∝e-U(xi|xNi),

(7)

P(xi|yi)∝e-U(xi|yi)。

(8)

将式(7)和(8)代入式(4)，并在等式两边同时取自然对数，便将乘积形式转化为求和形式，这样更利于计算最优解。转化过程为

(9)

(10)

于是，式(10)表示最大后验概率P(xi|yi)等价于最小化后验能量函数U(xi|yi)： U(yi|xi)为观测场中地物类别的第i个像素点的似然函数能量；U(xi|xNi)为标记场中第i个像素点对应的先验概率能量。因此，最终的能量关系可简写为

U(xFi|yi)=U(yi|xi)+U(xi|xNi)，

(11)

式中：xi为第i个像素点的当前分割标记；xFi为最终的分割标记。

1.3 能量函数计算

ICM算法执行过程如图1所示。

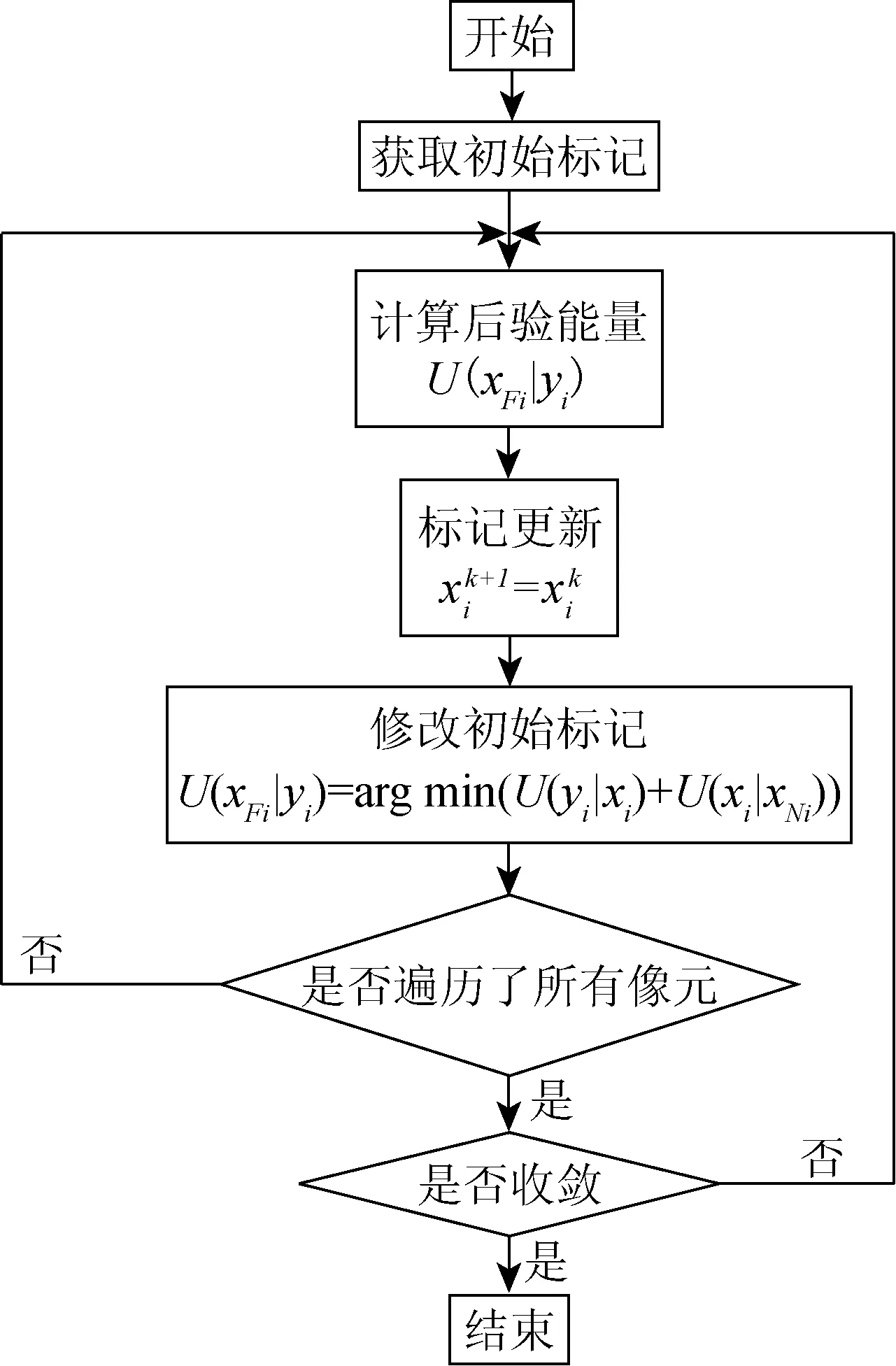
图1 ICM算法执行过程Fig.1 Execution process of ICM algorithm

2 算法改进

大部分遥感影像由于传感器的姿态变化以及周期性偏移等原因导致成像时带有噪声。这样的影像直接用于分割时，容易产生离散斑块和孤立点现象，有时甚至会出现错误分割的情况。针对这种情况，本文提出了将改进的ICM算法用于遥感影像分割的方法： 首先利用BF对遥感影像进行预处理，以提高影像的质量； 然后用多阈值最大类间方差法(Otsu)代替K-means作为获取初始标记的算法，用以克服K-means聚类算法类别数不易确定和算法复杂度不易控制等问题。

2.1 影像预处理

BF是一种保边去噪效果良好的滤波器。首先对遥感影像进行双边滤波，这样不但可以保留影像地物边缘，还可以去除影像噪声，增加影像对比度。BF由2个系数构成： 一个是由几何空间距离决定的滤波器系数，另一个是由像元差值决定的滤波器系数。

BF中输出像元的值，即对影像进行滤波操作后输出的像元值，依赖于对邻域像元值的加权，即

(12)

式中： (i,j)为影像中的任一像元； (i′,j′)为像元(i,j)邻域系统内的像元；f(i,j)为输入像元的值；g(i,j)为输出像元的值；w(i,j,i′,j′)为高斯核函数，由邻域系统内像元的核系数乘积构成，即

(13)

式中：hx和hy分别为由像元几何空间距离决定的定义域核和由像元差值决定的值域核。这2个核均为未知参数，但因篇幅所限，本文不再赘述参数的估计方法，为了计算方便，直接使用文献[14]中定义的参数。

2.2 初始标记获取

ICM算法是计算最小后验能量的常用方法。传统的ICM算法使用K-means聚类算法获取初始标记，该算法首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。此外，K-means算法需要不断地调整样本分类和计算调整后的新的聚类中心，因此，当数据量较大时，该算法耗用的时间和复杂度是非常大的。

本文采用Otsu法作为获取初始标记的算法，在划分L个类别C1,C2, ...,CL的情况下，多阈值类间方差可表示为

(14)

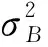
此外，为了保证分割的准确性，本文在类间方差法的基础上，引入类内方差，即

(15)

正确的分割分类结果应使类间样本离散度大，同时保证类内样本的聚集性好，这就要求在类间方差越大的基础上保证类内方差最小。综合考虑两者的关联度，本文采用可分性度量准则λ作为分割阈值。当λ达到最大值时，表示类间分离性和类内聚集性达到平衡，此时的阈值是最适合进行分割的最佳阈值。通过遍历影像直方图主峰的方式获得多个分割阈值λ，并确定初始分割类别数为λ+1。可将度量准则λ表示为

(16)

3 实验结果与分析

为了验证改进算法相对于传统ICM算法的优越性和通用性，本文分别采用航摄影像和多光谱卫星遥感影像进行了实验，并对分割效果进行了评价。分割效果评价首先从人眼视觉主观感受方面分析改进ICM算法用于遥感影像分割时的表现，其次引入分割准确率和Kappa系数对传统ICM算法、无滤波ICM和本文算法进行定量比较，最后从分割类数与Kappa系数的关系以及分割准确率与分割类数的关系对算法的鲁棒性进行分析。之所以选择分割准确率和Kappa系数作为定量评价指标，是因为研究过程中将分割看成是一种特殊的分类过程，因而可以用混淆矩阵(confusion matrix)对分割结果构建重叠矩阵(overlap matrix)进行评价。假设将影像分割为N类，将混淆矩阵的每一项Cij定义为同时属于分割算法标记的第i类和参考分割结果标记的第j类的像元个数，则分割准确率Accuracy定义为

(17)

3.1 实验一

选择科罗拉多大峡谷的航摄影像进行分割实验。科罗拉多大峡谷航摄影像(图2(a))由国际空间站2014年4月14日拍摄，该地区位于美国亚利桑那州西北部的凯巴布高原，总面积接近3 000 km2，影像大小为960像元×960像元。通过影像预处理，执行程序遍历影像直方图主峰的方式获得分割阈值个数为λ=7，因而确定初始聚类为8； 而目视判别影像区域可分为3个部分： 深色植被、浅色植被和其他地物，故确定分割类数为3。分割结果和分割精度分别如图2和表1所示。

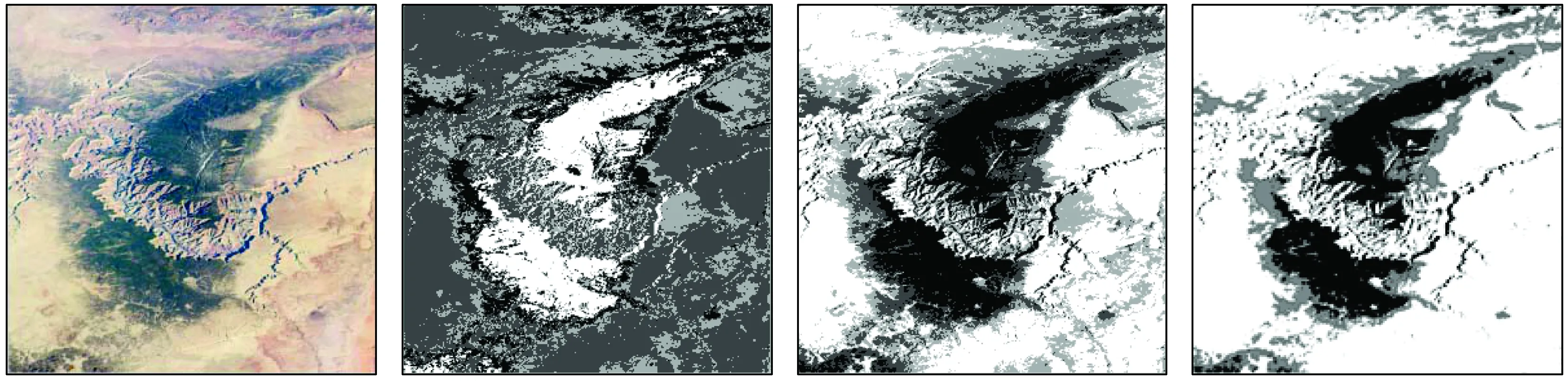
(a) 原始图像(b) 传统ICM (c) 无滤波ICM (d) 本文算法

图2 科罗拉多大峡谷航摄影像不同算法分割结果对比Fig.2 Comparison of segmentation results of Grand Canyon aerial image by using different algorithms表1 不同算法的分割精度Tab.1 Segmentation accuracy of different algorithms

仔细对比图2中的分割影像可以看出，传统ICM算法的分割效果一般，并且出现了一些离散斑块和孤立像元点； 无滤波ICM算法由于改进了初始标记的获取方式，分割效果与传统ICM算法相比有了一定的改善，但因原始图像没有经过滤波处理，分割效果与本文算法相比在边缘和细节方面的表现差了很多。本文算法通过改进初始标记获取方法和加入BF，使得分割效果明显优于前2种算法，并且在分割后的影像中边缘更加平滑，细节信息更加突出。此外，从表1中的数据可以看出，本文算法相比于传统ICM算法，在分割准确率上提高了18%，Kappa系数提高了14%，表明本文算法用于遥感影像分割时的结果更加准确。

3.2 实验二

选择印尼科摩多国家公园真彩色影像和阿拉胡埃拉湖多光谱影像进行分割实验。印尼科摩多国家公园真彩色影像(图3(a))是由Terra卫星搭载的高级星载热辐射和反射辐射计(advanced spaceborne thermal emission and reflection radiometer，ASTER)传感器于2000年7月20日获取的，影像大小为550像元×550像元。图3(a)中蓝色表示水，灰色表明裸露地面，绿色表示植被，白色表示云。初始聚类数为10，分割类数为4，实验结果如图3所示。

(a) 原始图像 (b) 传统ICM (c) 无滤波ICM(d) 本文算法

图3科摩多国家公园影像不同算法分割结果对比

Fig.3ComparisonofsegmentationresultsofKomodoNationalParkimagebyusingdifferentalgorithms

阿拉胡埃拉湖多光谱影像(图4(a))是由美国航天局Earth Observing-1(EO-1)卫星搭载的高级陆地成像仪(advanced land imager，ALI)于2010年12月17日获取的，影像大小为600像元×600像元。由于暴雨的影响，大量泥沙冲入该地区湖泊、河流中，导致水域颜色为黄色，图4(a)中白色表示云，其余地物可看成是植被。初始聚类数为12，分割类数为3，实验结果如图4所示。

(a) 原始图像(b) 传统ICM (c) 无滤波ICM (d) 本文算法

图4阿拉胡埃拉湖多光谱影像不同算法分割结果对比

Fig.4ComparisonofsegmentationresultsofAlajuelaLakemultispectralimagebyusingdifferentalgorithms

对比图3和图4的分割结果可以看出，用传统的ICM算法进行多光谱影像分割时，出现的错分现象比较严重，并且分割区域边缘不平滑。反之，本文算法无论在分割效果方面的表现，还是在分割区域边缘的表现，均优于传统ICM算法和无滤波ICM算法。

3.3 实验三

选择俄罗斯西伯利亚地区的Chara沙地Landsat 8多光谱卫星遥感影像和新西兰拉凯阿河航摄影像进行分割实验。

俄罗斯西伯利亚地区Chara沙地的Landsat 8多光谱影像(图5(a))于2013年9月获取，由11个波段组成，本次研究使用Band3(R)、Band2(G)、Band1(B)波段组合合成模拟真彩色影像，大小为1 712像元×1 712像元。影像中可分辨出的地物主要包括沙地、植被、云、湖泊、河流及其他等6类，初始聚类为10，分割类数为6，实验结果如图5所示。

(a) 原始图像(b) 传统ICM (c) 无滤波ICM (d) 本文算法

图5Chara沙地多光谱遥感影像不同算法分割结果对比

Fig.5ComparisonofsegmentationresultsofCharasandmultispectralremotesensingimagebyusingdifferentalgorithms

从图5可以看出，本文算法的分割结果均优于传统ICM算法和无滤波ICM算法。

图6示出实验三影像通过3种分割算法获得的Kappa系数与影像分割类别数目的关系。

图6 Kappa系数与分割类别数的关系Fig.6 Relationship between Kappa coefficients and number of clusters

从图6可以看出，当分割类数少于4时，3种分割算法均表现为低度一致性，说明3种算法对于简单地物类别的遥感影像分割效果均一般； 当分割类数介于5到8之间时，本文算法相比于传统ICM算法影像分割结果体现出了高度一致性； 而分割类数多于9时，由于地物类别复杂以及光谱特征相近等原因产生了一些误分割的现象，导致Kappa系数降低，但本文算法仍然具有中度一致性的分割结果。

图7(a)是选择的新西兰拉凯阿河航摄影像，大小为800像元×800像元。人眼从影像中可分辨出的地物包括耕地、人工林地、灌木林、草地、河边滩涂、水域和未利用土地等类型。通过遍历影像直方图主峰，确定初始聚类数为16，分割类数为8。实验结果如图7所示。图8示出图7中拉凯阿河航摄影像取不同分割类数时获得的分割准确率。

(a) 原始图像(b) 传统ICM (c) 无滤波ICM (d) 本文算法

图7拉凯阿河航摄影像不同算法分割结果对比

Fig.7ComparisonofsegmentationresultsofRakaiaRiveraerialimagesbyusingdifferentalgorithms

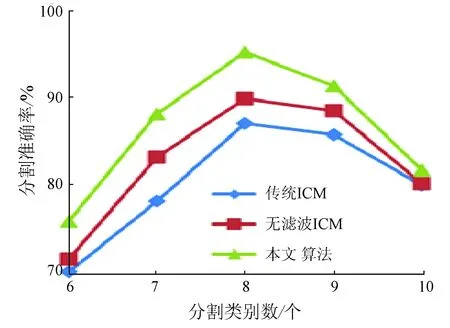
图8 拉凯阿河航摄影像分割准确率与分割类别数的关系Fig.8 Relationship between segmentation accuracy and number of clusters from aerial images of Rakaia River

从图8可以看出，本文算法的分割类数与实际类数一致，并在分割类数与实际类数有较小偏差时获得的分割准确率均高于传统ICM算法和无滤波ICM算法。

4 结论

针对传统的迭代条件模式(ICM)算法用于遥感影像分割时容易出现离散斑块和孤立点的现象，本文改进了传统的ICM算法。本文算法首先加入双边滤波器(BF)进行遥感影像预处理，在降噪的同时较好地保留了边缘信息； 然后用多阈值最大类间方差法(Otsu)代替原有的K-means算法，通过遍历影像直方图主峰的方式获取多个分割阈值，进而确定初始聚类数目，获取初始标记。本文算法克服了传统ICM算法中用K-means获取初始标记时类别数不确定和算法复杂度不易控制的问题。实验结果表明，改进的ICM算法用于遥感影像分割时分割效果优于传统ICM算法和无滤波ICM算法。

然而，对于地物类别复杂的遥感影像，利用本文算法进行分割时仍可能产生误分割和未分割现象，这将是今后的研究重点。