基于PageRank的产品方案设计SysML模型关键要素提取方法

蒋丹鼎，赵 颖

（1.国防科技大学 系统工程学院，长沙 410073；2.中国航天电子技术研究院，北京 100094）

0 引言

随着市场国际化以及企业间竞争的加剧，企业必须有快速开发新产品的能力以应对市场需求的不断变化。相关研究表明[1]，新产品开发中约80%的设计内容需要参考已有的设计知识或设计成果。从系统工程和已有设计成果重用的角度出发，方案设计可以理解为是对已有设计结果中要素的筛选、重用和创新[2]，而要素的筛选往往使用已有设计结果中的关键要素，因此提取出已有设计中存在的关键要素并发掘关键要素间的关联对提高新设计的质量和效率具有重要意义。

由于当前产品的设计复杂高、更新换代快，发掘已有设计结果中的关键要素面临两个方面的问题。一是在产品设计结果中包含要素繁多，难以分析其中要素的关键性；二是产品设计结果中要素间的关联关系交错复杂，难以梳理不同要素间的相关程度。在以往的关键要素提取研究中，MacCalman等人提出了从一个集成系统模型的试验设计中提取关键要素的MBSE方法论[3]，利用试验设计探索更大的设计空间并了解每个要素对结果产生的影响，此方法需要设计试验，实施难度较高；徐兰依据贝叶斯原理并利用经验数据集先验概率得到复杂质量系统中的关键质量要素[4]；MaZ采用从机械对称结构设计实例数据库中挖掘关联规则来实现对结构对称的设计知识在新的设计中的重用[5]。但这两种方法一方面需要使用大量结果数据，难以适应产品迭代的速度，另一方面忽略了关键要素间的相互联系，不利于关键要素的组合使用。

综上所述，产品的方案设计结果从整体上可以视为由设计要素间相互作用关系组成的网络，关键要素和关键要素间关联的提取就是从上述网络中提取出由关键要素组成的子网络。与此类似，网页排名算法的目标是从网页相互引用组成的网络中提取高质量的网页，我们可以将高质量的网页看作关键要素，而把与之互联的网页链接关系看作关键要素与其他要素之间的连接。同时，基于模型的系统工程（model-based systems engineering，简称MBSE）及其标准建模语言SysML已经成为复杂产品方案设计的重要方法[6～8]，因此本文以产品SysML模型中的关键要素提取为目标，借鉴面向互联网互联网页排名算法PageRank，提出了设计关键要素的提取算法KEERank（Key Elements Extraction with PageRank）。

1 KEERank方法原理

Google PageRank算法的思想精华在于：将一个网页级别（重要性）的排序问题转化成了一个公共参与、以群体民主投票的方式求解的问题，网页之间的链接即被认为是网页间的投票行为[9]。产品SysML模型中关键要素的提取问题与网页排序问题相同的是需要评价网络中节点重要性，与网页排序问题不同的是产品SysML模型中模型元素间的关系复杂多样，难以评估不同关系对模型元素重要性的影响。根据上述分析，基于PageRank的产品SysML模型关键要素提取方法主要需要解决以下两个问题：一是如何判断产品SysML模型中模型元素间不同关系对模型元素重要性评估的影响程度，二是如何在已知不同关系对模型元素重要性评估影响大小的情况下对节点重要性进行合理评估。

KEERank方法共包含两个步骤，第一步是将产品SysML模型转化为有向加权图，第二步是利用有向加权图评估模型元素的重要性进而获取其中的关键要素。产品SysML模型M可以描述为M=（S，E），其中S表示模型元素的集合，E是模型元素间关系的集合。产品SysML模型对应的有向加权图即系统加权图可以描述为WG=（S，E，W），其中S和E与M中的S和E相同，W表示权重集，是E中关系元素所对应的关系强度。关系强度的定义如下：

定义1：关系强度（linkingstrength，简称ls）是模型元素间特定类型关系e的连接强度，说明元素之间关联关系的强弱。

对于任一类型的模型元素间关系e∈E都有一个强度描述函数来反映其连接强度：ls(e)=a，a∈(0,1]为常数，表示e的关系强度值。

KEERank方法的第一步通过计算模型元素间不同关系类型所对应的关系强度，从而将产品SysML模型M转化为系统加权图WG。为了分析模型元素间不同关系类型所对应的关系强度，本文运用层次分析法对不同关系所对应的关系强度进行计算。

KEERank方法的第二步是要解决系统加权图中节点重要性的评估问题。关于有向加权图中节点重要性的评估方法，已经存在相关研究[10]，本文结合关键要素提取的特点与该研究成果，基于PageRank算法评估产品系统加权图中的模型元素的重要性。

2 基于关系强度的模型转换

产品SysML模型中的九种视图可以分为需求、功能和结构三个部分[11]（如图1所示），需求部分描述了产品的存在价值，行为部分说明了产品功能的实现形式，结构部分体现了产品的组成元素及其元素间的作用关系。三部分虽然各有侧重点，但是结构部分作为行为的载体以实现产品功能，反映了设计结果中最根本的内容，因此下文将针对产品SysML模型中的结构部分进行分析。

图1 产品SysML模型中所包含的视图分类

产品SysML模型到系统加权图的转换需要首先从模型M中获取元素集合S及其关系集合E，然后评价不同模型元素间关系的关系强度并进而得出系统加权图WG中的W集合中的元素，进而得到系统加权图WG。为了探讨产品模型结构部分中模型元素间的相关关系，本文根据文献[12]将SysML结构图中模型元素间关系表达总结为5种，如表1所示。

根据表1，本文对不同模型元素间关系定义及其方向的说明如下：交互关系记作ia(si，sj)，根据建模时对应的接口或流属性来确定，方向与建模时表达方向一致；约束关系记作cs(si，sj)，方向为双向关系;引用关系记作rt(si，sj)，方向与建模时表达方向一致；分解关系记作di(si，sj)，在分解关系的提取中，复合关联关系根据建模方向拆解为一对或两对关系，每个结构属性与模块发生双向关系；依赖关系记作ro(si，sj)，在关系提取中，将受某一模型元素影响的模型元素与该模型元素建立依赖关系，方向与建模时表达方向一致。模型元素si指向sj的类型为f的关系可以描述为其中

为了获得上述五种关系对应的关系强度，采用层次分析法实现计算，步骤如下:

步骤1：构建递阶层次结构模型。如图2所示，将目标层设为确定不同关系类型的关系强度，方案层即为五种关系，在策略层提出2个评价准则：约束强度F1和元素间距离F2。约束强度指的是关系能够体现的两个元素间的相关程度，元素间距离指的是关系的灵活程度。以分解关系和交互关系为例，分解关系只能作用于有从属关系的要素之间，而交互关系可以联系不同层级的系统，相较来说，分解关系的约束强度高，交互关系能够约束的模型元素间距离大。

步骤2：用成对比较法和1-9比较尺构造比较矩阵。评价准则F1、F2对目标的比较矩阵为A，五种关系对F1、F2的比较矩阵为

表1 SysML模型中的模型元素间相关关系提取

图2 关系强度评估的层次结构模型图

表2 评价因素对目标的比较矩阵A

表3 五种关系对F1的比较矩阵B(3)1

步骤3：计算单层排序权向量，并做一致性检验。对每个对比较矩阵计算最大特征值及其对应的特征向量，然后根据计算一致性指标比，其中n为比较矩阵中包含元素的个数。比较矩阵A为二阶矩阵，满足一致性要求，其特征向量归一化后为w(2)=[0.75, 0.25]T。比较矩阵B1(3)和B2(3)计算结果如表所示，其中当n=5时，查表得RI=1.12，通过一致性校验。

表4 五种关系对F2的比较矩阵

表4 五种关系对F2的比较矩阵

F2 cs ia rt di ro cs 1 1/3 1/3 5 1 ia 3 1 1 7 3 rt 3 1 1 7 3 di 1/5 1/7 1/7 1 1/5 ro 1 1/3 1/3 5 1

表5 比较矩阵B1(3)和B2(3)的权向量计算结果

表6 五种关系的关系强度

计算出模型元素间不同关系类型对应的关系强度后，根据产品SysML模型M中关系类型E获得相对应的关系强度，即可生成系统加权图WG中的模型元素间关系强度集合W。

3 基于PageRank的关键要素提取

根据PageRank算法的原理，评价模型元素的关键性必须引入邻接矩阵，然后借助邻接矩阵建立概率转移矩阵Q，并迭代求解计算模型元素的重要性，最后调整权值从模型元素中筛选关键要素。由于产品SysML模型的特殊性，在使用系统加权图构建邻接矩阵时，有可能存在两个模型元素间存在两个及两个以上关联的情况，因此本文引入了贡献度的概念来描述邻接矩阵中两个模型元素间的联系强弱。

定义2：贡献度lss是两个模型元素间全部关系所对应的关系强度之和，反应了模型元素间的联系强弱，计算方式如下：

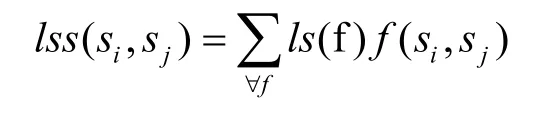
其中f(si, sj)是判断模型元素si到sj是否存在类型为f的相关关系，若存在，则f(si, sj)=1，反之f(si, sj)=0。

根据模型元素间的贡献度计算方法将产品系统加权图转化为邻接矩阵M。

以液压缸系统加权图中的部分为例，其邻接矩阵的构建方法如图3所示，其中邻接矩阵第i行第j列对应的值为以第i行对应元素为起始模型元素，以第j列对应元素为目标模型元素的所有模型元素间关系对应的关系强度之和，若关系强度为0，则此处取值为1/n。

图3 液压缸系统加权图模型(部分)到邻接矩阵的转换

算法：基于PageRank的关键要素提取。

输入：系统加权图WG。

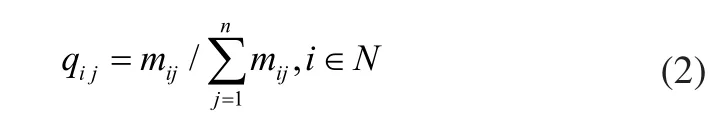
步骤3：根据式(3)，迭代计算设计元素的重要度。

其中，σ(0＜σ＜1)为阻尼系数，n是模型元素的总个数，E为元素全为1的n阶方阵。计算时取NR0为元素都为1/n的1×n阶矩阵。

每次迭代过程会更新NR矩阵的值，等到前后两次NR值的差值小于某个接近0的数时，结束迭代过程，此时NR值对应了要素的重要程度。

步骤4：通过动态设置阈值σ，从要素中筛选不同层次的关键要素。

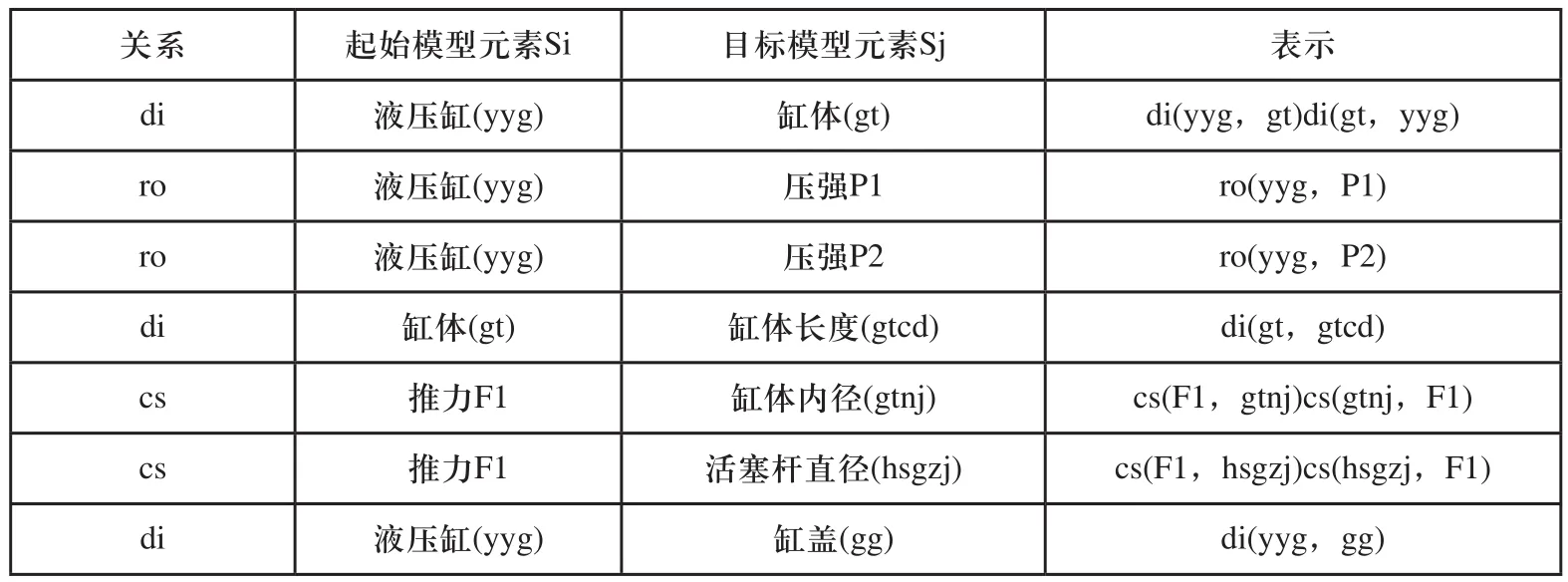
表7 液压缸模型元素间的关联关系局部

4 验证

以单杆活塞式液压缸的SysML模型[13,14]为例，本节首先从系统模型中获取模型元素集合S和模型元素间关系集合E，依据模型元素间不同关系种类对应的关系强度将SysML模型转化为系统加权图，然后根据模型元素间的贡献度计算方式求解出液压缸系统的邻接矩阵和邻接矩阵对应的概率转移矩阵，最后使用迭代计算的方式求解出液压缸系统中模型元素对应的重要度矩阵。其中关键步骤及对应结果如下。

分析单杆活塞式液压缸的SysML模型提取到的部分模型元素及模型元素间的关系如表7所示。

计算模型元素间的贡献度，并进一步得到邻接矩阵图如表8所示。

根据邻接矩阵构建概率转移矩阵Q，并根据基于PageRank的关键要素提取算法评价模型元素的重要性，得到模型元素对应的NR值，如表9所示。从表8中可以看出，导向套是当前液压缸系统中重要性评价最高的模型元素，这也反应了此液压缸拥有较高精度的特点。

随着方案设计过程的深入，设计者对当前系统的关注将逐渐偏移到重要度较低的要素。因此，我们可以通过动态调整关键要素的筛选阈值σ，查看不同层级结构中的关键要素。σ越小表示要查看设计要素的重要性越低，就越依赖于其它要素或者该要素对其他要素的影响越弱。例如：图4和图5是σ分别取=1.1和0.55所获得的关键要素可视化图。在图4中，压力P1、P2并不属于关键要素，随着设计进程的推进，取较低的阈值之后，在图5可以看见这两个要素。

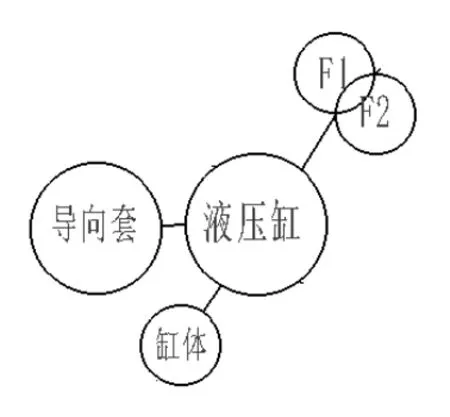
图4 σ=1.1时液压缸SysML模型中关键要素的分布图

图5 σ=0.55时液压缸SysML模型中关键要素的分布图

表8 液压缸产品对应的邻接矩阵（部分）

表9 液压缸系统模型模型元素及其NR值（部分）

同时，根据邻接矩阵中设计要素的关联关系，我们可以快速地从历史设计结果中取得与关键要素相关的其他设计要素，更好地分析设计变更的传播影响，从而节约设计者时间，加快方案设计的进程。例如，从满足液压缸推力设计的角度出发，在表8中提取所有与推力相关的关键要素及其对应的贡献度如表10所示。

表10 与推力元素F1相关的关键要素及其贡献度

5 结束语

本文提出了一种关键要素的提取方法KEERank，通过将产品SysML模型转化为系统加权图，然后利用考虑权值的PageRank方法来提取关键要素。与仿真方式或者根据使用结果反馈结合概率推算的方式相比，KEERank方法一方面不需要进行试验设计或者收集反馈信息，另一方面求解速度与上述方法差异不大，因此从总体上来说时间短、效率高，并且对使用者的要求低，只要具有相应的历史产品SysML模型，就能将模型元素的重要程度评估出来。通过实例验证可以发现，关键要素的提取能够为设计人员提供了思考的切入点和优化的核心，帮助设计者快速理解并重用已有设计结果。

本文中的关键要素挖掘主要针对系统模型中的结构设计部分，而需求设计与行为设计都尚未涉及，未来需要全面研究系统模型，能够在不同的设计阶段为设计人员提供相应的关键要素。此外本文中对于关键要素阈值的设定尚无有效的方法，有待进一步研究。