基于惯性基准法的高速铁路纵断面线形平顺性研究
李帅,易杨明,王源,陈嵘,王平
基于惯性基准法的高速铁路纵断面线形平顺性研究
李帅1,易杨明2,王源1,陈嵘1,王平1
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031;2.成都铁路局,四川 成都 610082)
为研究线路竖曲线引起的长波高低不平顺超限问题,采用基于惯性基准法的虚拟轨检技术,建立高速列车—线路动力学仿真模型,通过车体加速度与车体−车轮相对位移反演得到虚拟不平顺,进而分析列车检测速度,竖曲线半径、长度、坡度差、夹坡段长度等竖曲线基本参数对虚拟不平顺的影响规律。分析结果表明:检测速度与竖曲线半径对虚拟长波不平顺影响较大,同时将计算结果与规范对比,建议对于设计时速为300 km/h的高速铁路,在设计允许的条件下,竖曲线长度和夹坡段长度设计值应大于500 m。
高速铁路;惯性基准法;虚拟轨检技术;线路纵断面;长波不平顺
轨道不平顺是引起机车车辆与轨道结构产生振动的主要激扰源[1],而轨道不平顺是客观存在的,它的存在会导致轮轨间产生动力响应,从而影响列车运行安全和旅客舒适度[2],因此,严格控制各种初始不平顺,对保持轨道的良好状态,延长轨道部件寿命,减少维修工作量十分重要[3]。根据某线动检车数据发现,在竖曲线及其附近区段长波长高低不平顺波形出现异常突变情况,且现场反馈长波不平顺对高速铁路列车运行的舒适性和平稳性有着非常显著影响。因此,有必要对高速铁路纵断面线形出现的长波长高低不平顺异常情况进行探索。吴晓峰[4]以杭长客专上海局管段为例,对其竖曲线地段长波高低不平顺的超限情况进行统计分析,但仅得到了在时域上长波高低不平顺超限情况与线路纵断面线形参数及检测车速度等的关系。我国对高速铁路线形参数的优化设计已有较多的研究,研究方法主要有2种:一是建立基于线路参数的舒适度评价模型,通过分析舒适度指标得到线形参数的优化建议值[5−7];另一种是建立车—线动力学仿真模型,通过分析动力学指标得到建议值[8−9]。但以上研究均未从轨道平顺性角度分析参数的优化问题。因此,本文从轨道平顺性角度分别从时频域上探究线路线形各参数对轨道长波高低不平顺的影响。基于惯性基准法,建立高速列车—线路动力学仿真模型,结合轨检车的检测原理,模拟轨检车检测高低不平顺(即虚拟轨检技术),通过将测得的列车加速度与列车−车轮相对位移反演得到虚拟不平顺,进而分析列车检测速度,竖曲线半径、长度、坡度差、夹坡段长度等竖曲线基本参数对虚拟不平顺的影响规律。最终得到影响纵断面线形平顺性的主要因素并提出部分参数设计建议值。
1 基于惯性基准法的虚拟轨检车技术
为研究不同列车速度及纵断面线形参数对线形平顺性的影响,应用动力学软件建立具有二系悬挂系统的8节编组动车全车模型(见图1),采用基于惯性基准法的虚拟轨检车技术获得初始信号,再通过对初始信号的预处理和频域积分得到虚拟不 平顺。

图1 8节编组动车组模型
1.1 惯性基准法
惯性基准法是利用惯性原理获得测量基准的现代先进检测方法[10]。通常包括:惯性位移法(即振动质量法)、轴箱加速度积分法[11]、弹簧系统加速度积分与位移相加法。前2种方法由于可测波长范围较窄等缺点,仅个别国家、少数研究机构曾采用过。只有第3种方法被大部分国家的现代轨检车普遍应用,成为实用化的“惯性基准法”,因此,本文采用该方法作为理论基础。该方法中高低不平顺表示如下[12]:
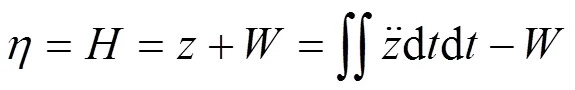
1.2 初始信号预处理
通过基于惯性基准法的虚拟轨检车技术得到虚拟初始信号,本文收集的初始信号包括车体加速度、车体−轴箱间相对位移,但根据研究及实际需要,只需保留120 m以下的波长成分,因此,本文将得到的虚拟信号进行数字滤波。其中数字滤波频域方法的表达式为[13]:
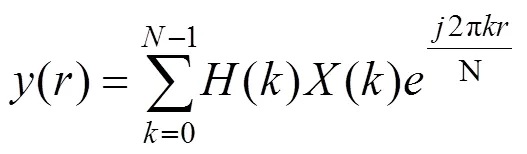
式中:为输入信号的离散傅里叶变换;为滤波器的频域响应函数,由此可确定滤波器的功能,即滤波截止频率(波长)范围,本文所采用的高通滤波器的频响函数为:
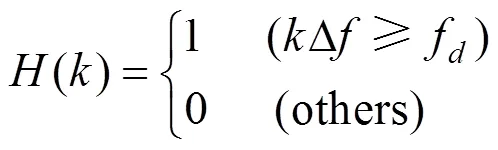
式中:f为下限截止频率;Δ为频率分辨率。
数字滤波器频域方法的特点是方法简单,计算速度快,滤波频带控制精度高。但是由于对频域数据在截止频率处的突然截断造成的谱泄露会造成滤波后的时域信号出现失真变形,因此,本文中的滤波器在通带和阻带之间进行了平滑衰减过渡,其频响函数曲线如图2。
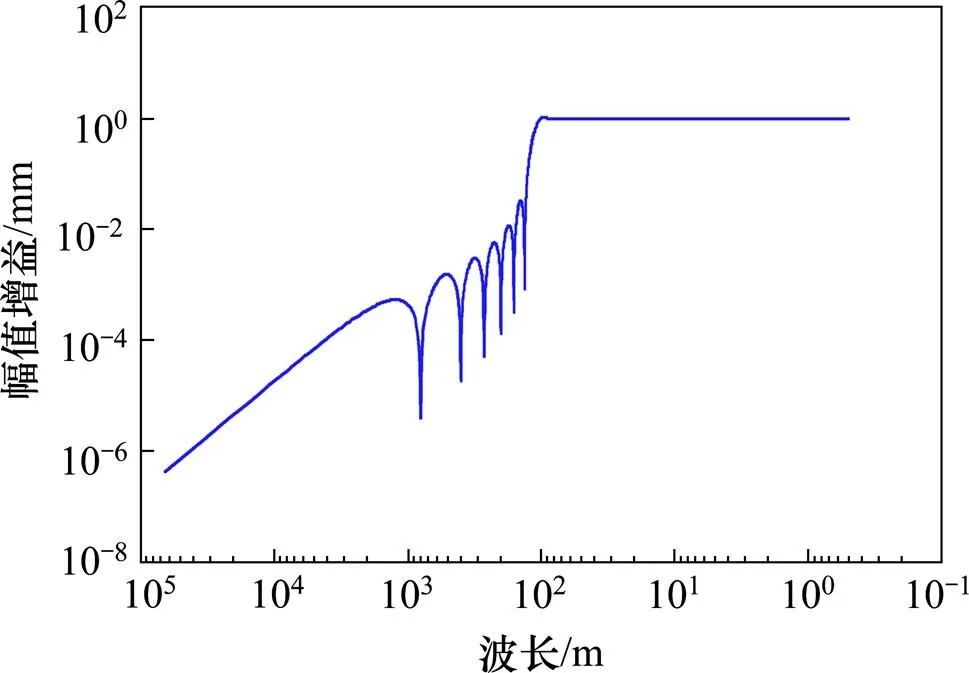
图2 高通滤波器幅值响应函数曲线
1.3 初始信号频域积分
由于频域积分可以有效避免时域信号的初始微小误差在积分过程中的累积放大作用,相较于时域积分更准确和稳定。而且本文需要的120 m以下波长对应的低频能满足要求,因此本文对加速度信号采用频率积分。
频域积分的基本原理就是首先将需要积分的信号()作Fourier变换,然后利用Fourier的积分特性得到()积分后的频谱,最后经Fourier逆变换得到积分后()的时域信号。
据傅里叶逆变换,加速度在任一频率的傅里叶分量表达式为:
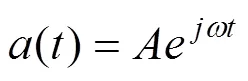
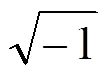
当初速度和初位移分量均为0时,对加速度信号分量分别进行一次积分和二次积分,可得速度信号分量和位移信号分量:
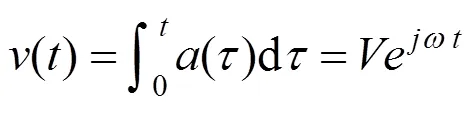
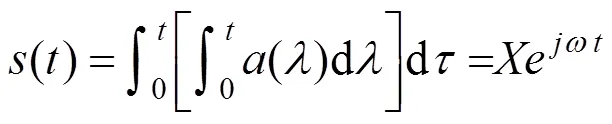
式中:()和()分别为速度信号和位移信号在频率的傅里叶分量;和分别为对应()和()的 系数。
1.4 虚拟轨检方法验证
应用本文基于惯性基准法的虚拟轨检车技术,使列车在直线段运行,将软件模拟条件下的虚拟高低不平顺与激励不平顺通过时频域评价指标作对比,时域评价采用200 m区段为信号单元长度,以10个数据点为步长(即2.5 m)滑动进行计算得到标准差曲线,频域评价指标采用功率谱密度,从而验证该方法的正确性。
为保证软件计算结果的真实性,需要对轨道添加一段初始激励不平顺使列车在垂向激振下运行,本文的激励不平顺基于德国低干扰高速谱反演生成。由于本文主要分析长波长对轨道平顺性的影响,因此激励不平顺波长范围取为0.1~10 m。列车分别在检测速度250,300和350 km/h下高速运行,通过动力仿真得到虚拟高低不平顺,图3即为虚拟不平顺与激励不平顺的对比。
由图4可知高低虚拟不平顺同其激励不平顺在幅值和波形上都能非常好的复合。
由图4(a)可知,虚拟不平顺的标准差与激励不平顺的标准差均呈周期性变化,但虚拟不平顺的标准差较激励不平顺的标准差略有0.05 mm左右的增大。由于计算结果经过了列车动力学模型、二次积分及高通滤波等一系列过程的干扰,故本文认为该增大处于本文研究的合理范围之内,因此可以说明在时域上虚拟不平顺和激励不平顺标准差是基本一致的,且虚拟不平顺标准差不受仿真速度的影响。由图4(b)可知,虚拟不平顺的轨道谱与激励不平顺的轨道谱曲线基本吻合,因此可说明,在不同检测速度下基于惯性基准法得到的虚拟不平顺与激励不平顺的波长成分基本相同。
综上可说明:本文设计的基于惯性基准法的虚拟轨检车技术得到的虚拟不平顺能很好地反映激励不平顺在幅值以及波长成分2个方面的信息,因此该方法正确。
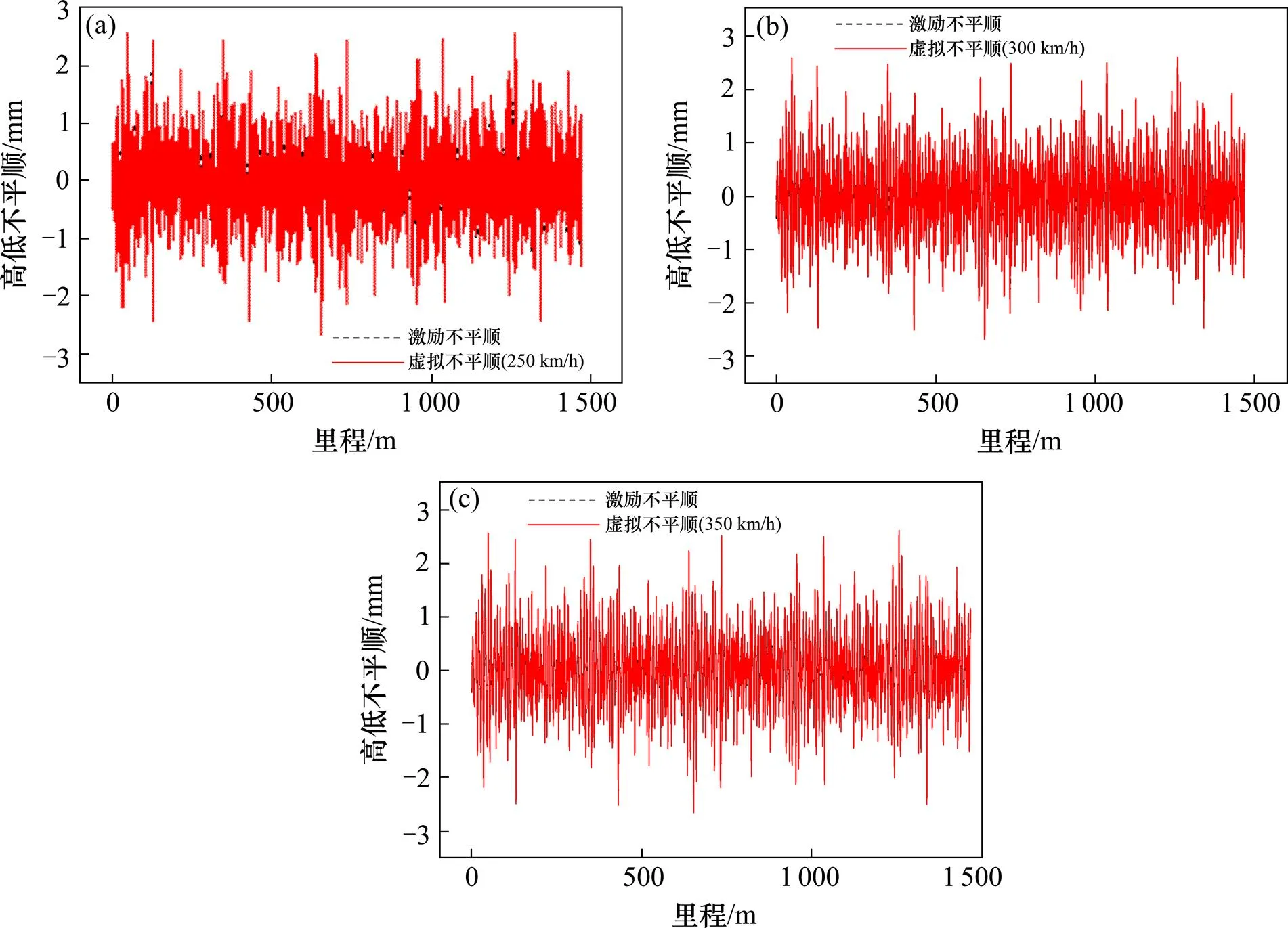
图3 不同检测速度下虚拟和激励不平顺波形曲线
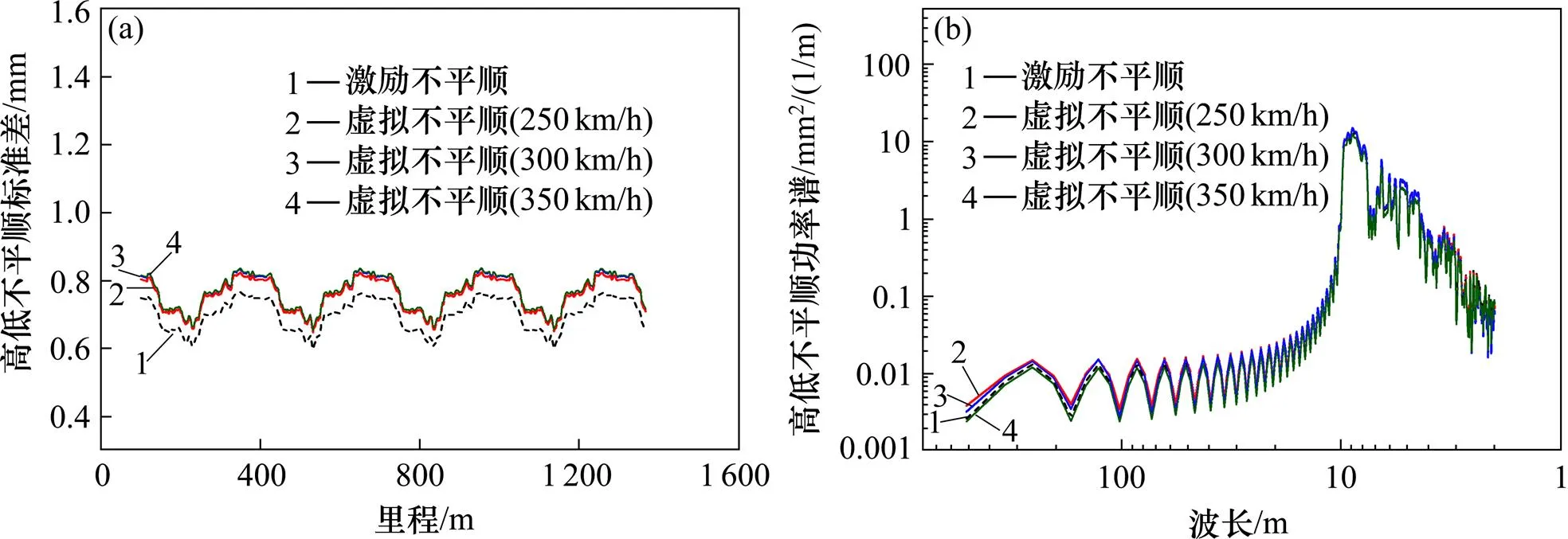
(a) 标准差对比图;(b) 轨道谱对比图
2 线路纵断面线形平顺性评估
已验证了本文所建立模型和方法的正确性,故在此应用上述模型和方法对影响线性平顺性的各因素展开分析。主要考虑以凸形竖曲线为代表的线路纵断面的高低不平顺,通过改变列车检测速度,竖曲线长度,坡度,坡度差Δ,竖曲线半径和夹坡段长度Δ等线形参数,分别研究基于惯性基准法的虚拟轨检车技术得到的虚拟不平顺与原始激励不平顺在时域和频域上的对比变化,从而得到影响纵断面线形平顺性的主要因素。
本节所用的高低激励不平顺均采用德国低干扰谱反演生成的幅值在±2.5 mm左右,截止波长范围在0.1~10 m的随机谱。
2.1 列车检测速度对纵断面线形平顺性的影响
主要研究列车检测速度对纵断面线形平顺性的影响,具体线形设置见表1。

表1 不同检测速度下的线形工况
通过动力学软件计算得到3种检测速度下的虚拟不平顺,由于线路过长,故本节以竖曲线中点为里程零点,向左右方向各取1 000 m作为时频域分析的样本,分析结果见图5(a)。
由图5(a)可知,虚拟不平顺标准差曲线在直坡段和圆曲线中点处与激励不平顺变化规律基本相同,幅值只是轻微提高。但是在竖曲线直圆点和圆直点附近出现了2个尖形“驼峰”。随着检测速度的提高,标准差峰值随之增大,说明检测速度对虚拟不平顺的幅值影响较大。
由图5(b)可知,在波长小于10 m时虚拟不平顺与激励不平顺的轨道谱图走势和幅值基本相同,但在波长大于10 m后,虚拟不平顺功率谱密度曲线出现长波长成分,且随着检测速度的提高,波长及功率谱密度值均随之提高,说明检测速度对虚拟不平顺的波长成分影响较大,与文献[14]得到的结论相同。
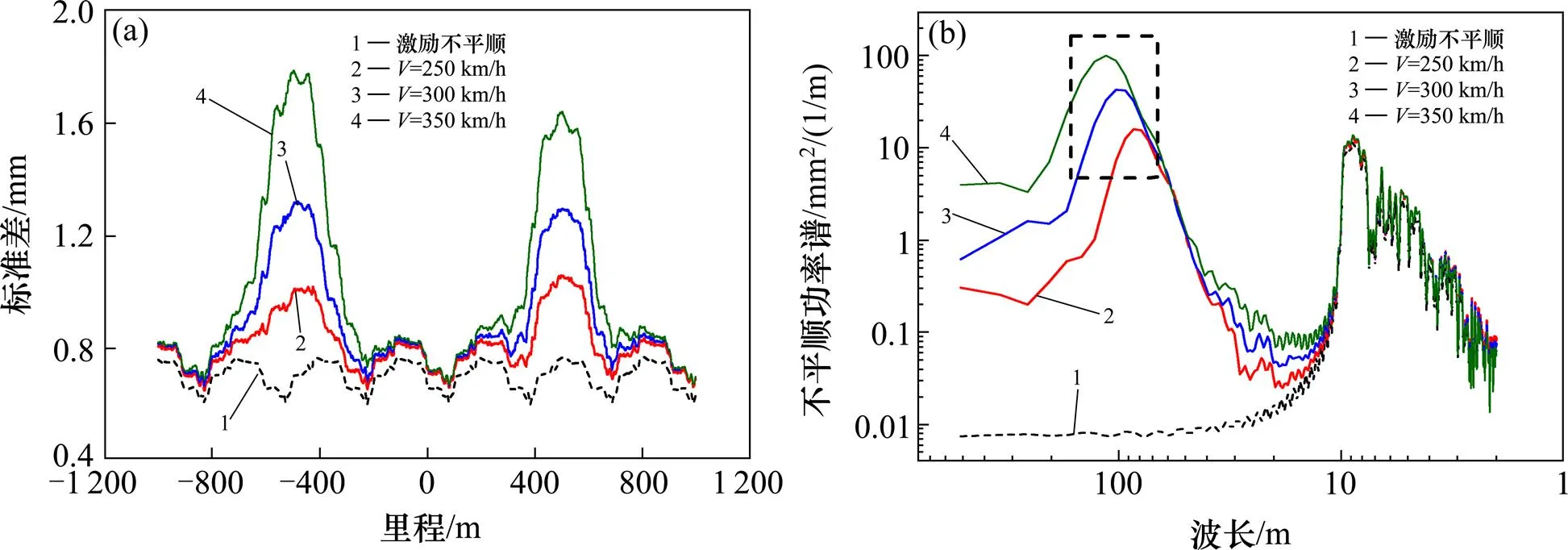
(a) 标准差对比图;(b) 轨道谱对比图
综上可知,列车检测速度是影响虚拟不平顺幅值和波长的重要因素,即对纵断面线形平顺性影响较大。
2.2 竖曲线坡度和长度对纵断面线形平顺性的影响
由于凸形竖曲线长度与竖曲线半径和坡度三者之间满足公式=(1−2),三者之间相互关联,故2.2~2.4小节分别控制一个因素,改变其他2个因素从而得到影响线形平顺性的主要因素。
控制竖曲线半径不变,改变坡度和竖曲线长度,竖曲线线形工况设置见表2。
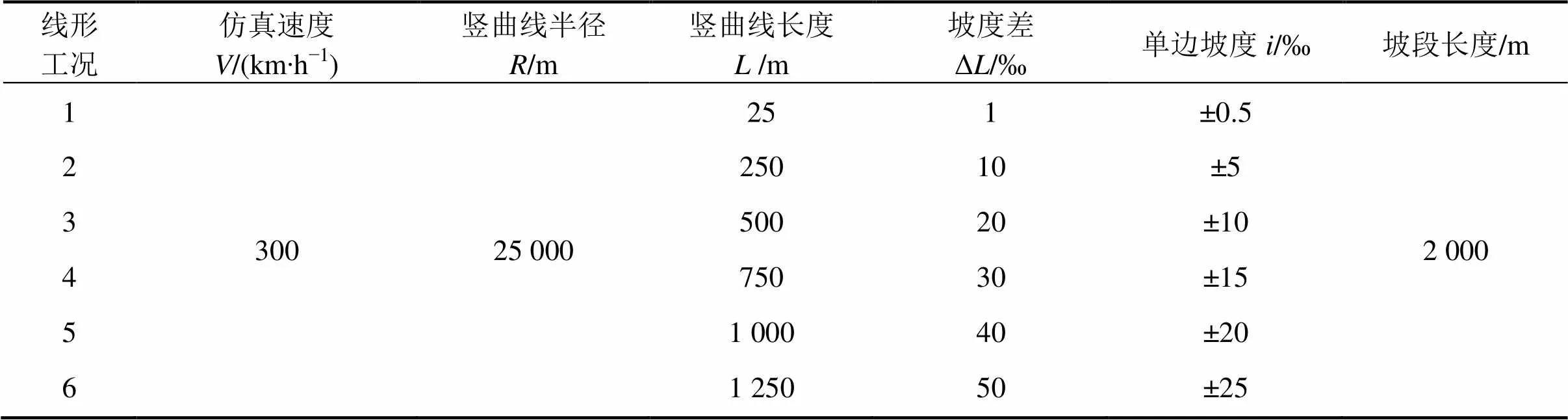
表2 不同竖曲线坡度和长度下的线形工况
通过动力学软件计算得到6种工况下的虚拟不平顺,由于线路过长,故本节以竖曲线中点为里程零点,向左右方向各取1 000 m作为时频域分析的样本,应用时频域分析方法对比虚拟不平顺与激励不平顺,对比结果见图6。
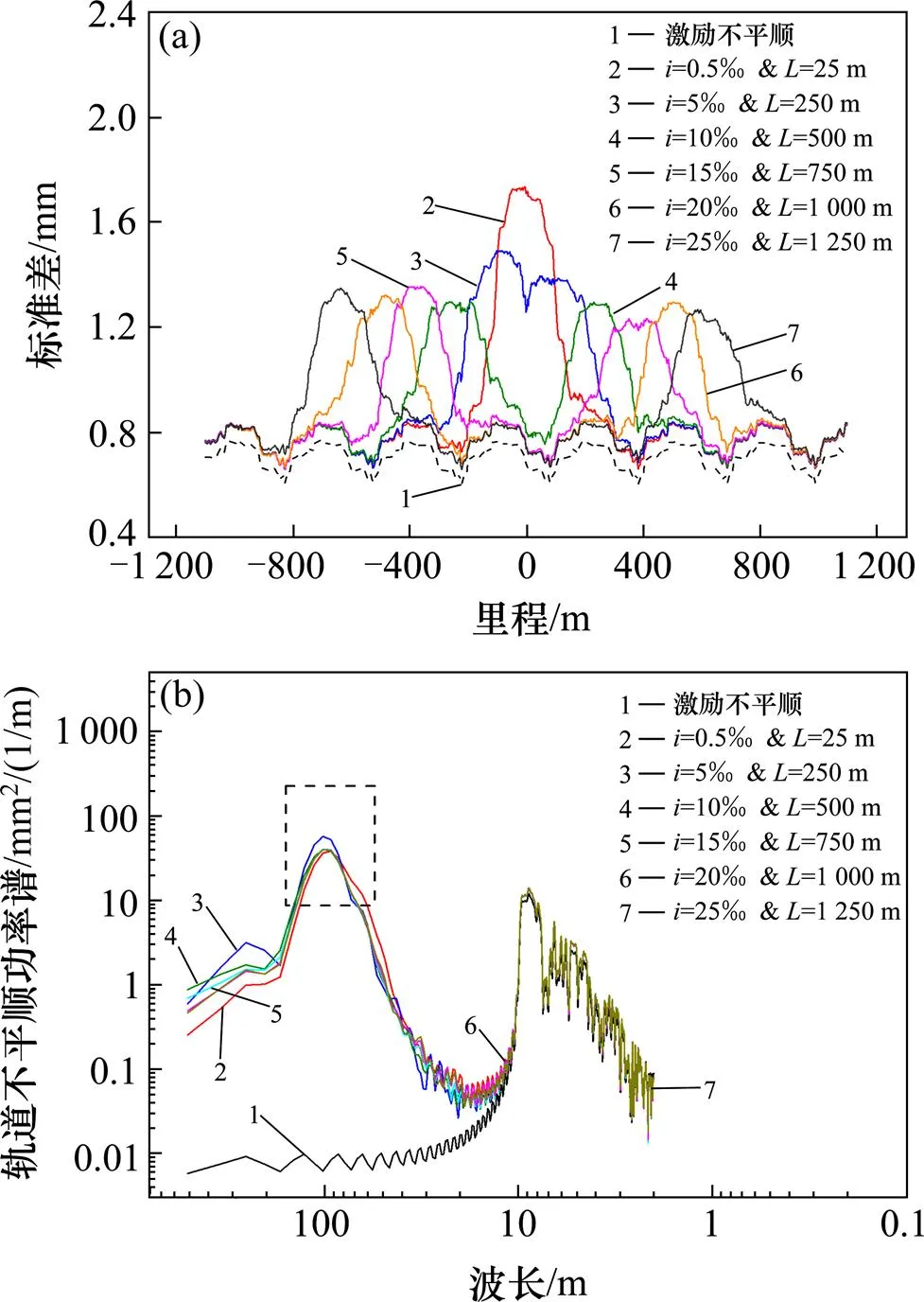
(a) 标准差对比图;(b) 轨道谱对比图
由图6(a)可知,对于竖曲线长度(坡度)较小,即竖曲线长度较短的工况1和2,竖曲线直圆点和圆直点2处产生的虚拟不平顺相互影响并叠加,在竖曲线中点附近产生了较大的幅值。随着坡度和竖曲线长度的增大,竖曲线直圆点和圆直点之间的影响越来越小,“驼峰”逐渐分离且其数值逐渐趋于稳定,最终在1.3 mm左右。
由图6(b)可知,不同坡度及竖曲线长度情况下虚拟不平顺所包含的波长成分基本相同,长波均为102.4 m,且除工况1和2由于叠加导致长波长的功率谱密度值不稳定外,其余工况均大致稳定在40 mm2/(1/m)左右。
2.3 竖曲线半径和坡度对纵断面线形平顺性的影响
控制竖曲线长度不变,改变竖曲线半径和坡度,竖曲线线形工况见表3。
同上节类似以竖曲线中点为里程零点,向左右各取800 m作为时频域分析的样本,分析结果见图7。
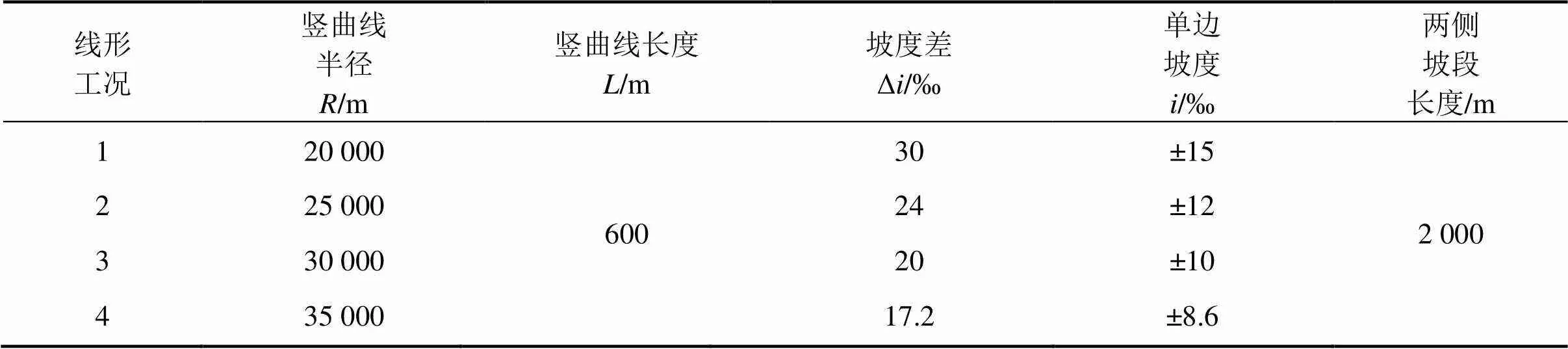
表3 不同竖曲线半径和坡度下的线形工况
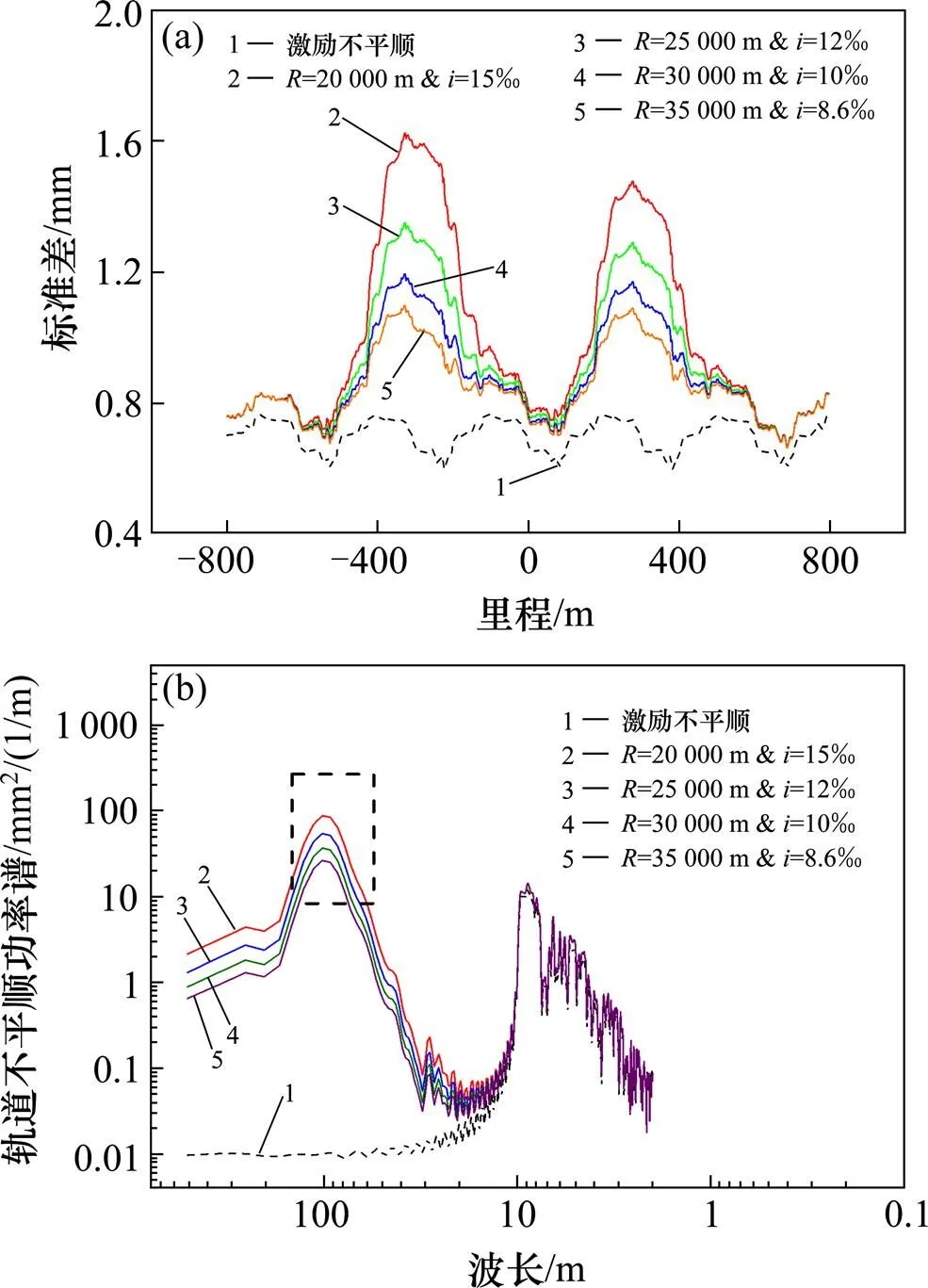
(a) 标准差对比图;(b) 轨道谱对比图
由上节可知,坡度对标准差幅值基本无影响。故由图7(a)可知竖曲线半径是影响标准差曲线幅值的主要因素,且将图6(a)与7(a)对比可知,竖曲线长度是影响左右峰里程的唯一因素。综上可说明竖曲线半径是影响虚拟不平顺的主要因素。
同理由上节可知,坡度对轨道谱图基本无影响,故由图7(b)可知竖曲线半径不影响轨道谱所对应的长波成分,但竖曲线半径对功率谱密度值有较大影响。因此,可说明竖曲线半径是影响虚拟不平顺的主要因素。
综上,竖曲线半径是影响虚拟不平顺的主要因素,即竖曲线半径对纵断面线形平顺性影响较大。
2.4 竖曲线半径和长度对纵断面线形平顺性的影响
控制坡度不变,改变竖曲线半径和长度,竖曲线线形工况设置见表4。
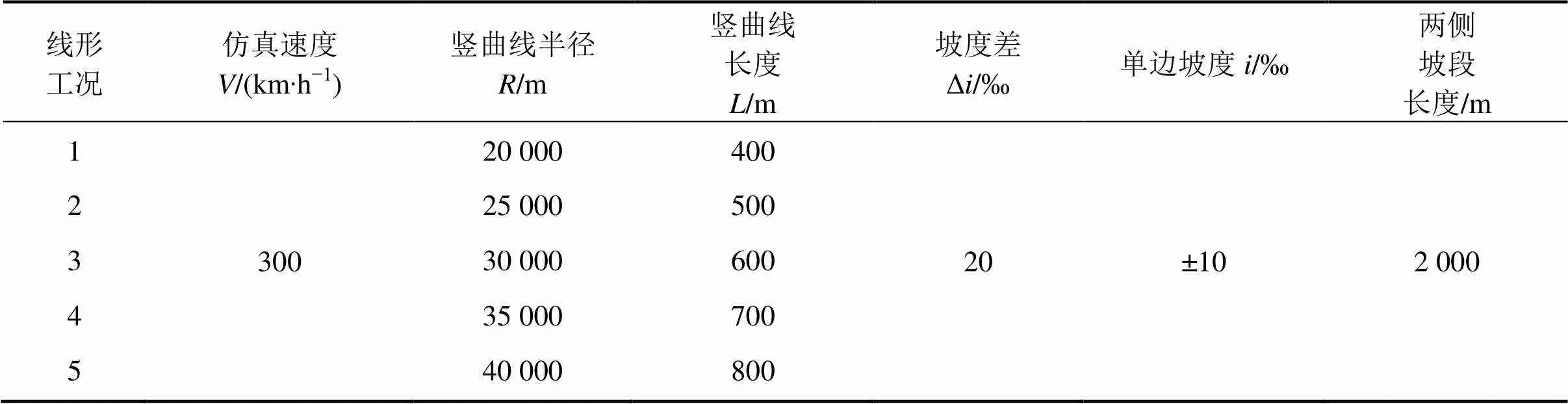
表4 不同竖曲线半径和长度下的线形工况
同上节类似以竖曲线中点为里程零点,向左右各取800 m作为时频域分析的样本,分析结果见 图8。
由图8(a)和以上规律综合可知,竖曲线长度是影响左右峰里程的唯一因素,而竖曲线半径是影响标准差幅值的重要因素。
同理,由图8(b)和以上规律综合可知,竖曲线半径不影响虚拟不平顺所包含的波长成分,长波均为102.4 m,但对长波的功率谱密度值影响较大。
综上可知,竖曲线半径对纵断面线形平顺性影响较大。且在竖曲线长度满足不叠加的要求(长度大于500 m)后,竖曲线长度不是影响虚拟不平顺的主要因素,即竖曲线长度对纵断面线形的平顺性影响较小。将所得结论与我国《高速铁路设计规范》对比,规范中规定:最小竖曲线长度不得小于25 m[15],由此可知,规范中的要求较宽松,为保证竖曲线设计时不产生初始不平顺,本文建议:对于设计时速为300 km/h的高速铁路,在设计竖曲线时长度需保证大于500 m。
3.5 夹坡段长度对纵断面线形平顺性的影响
控制运行速度,坡度,竖曲线半径和长度,改变夹坡段长度,竖曲线线形工况见表5。
通过动力学软件计算得到不同夹坡段长度下的虚拟不平顺,应用时域分析方法对比虚拟不平顺与激励不平顺,对比结果见图9(a)。
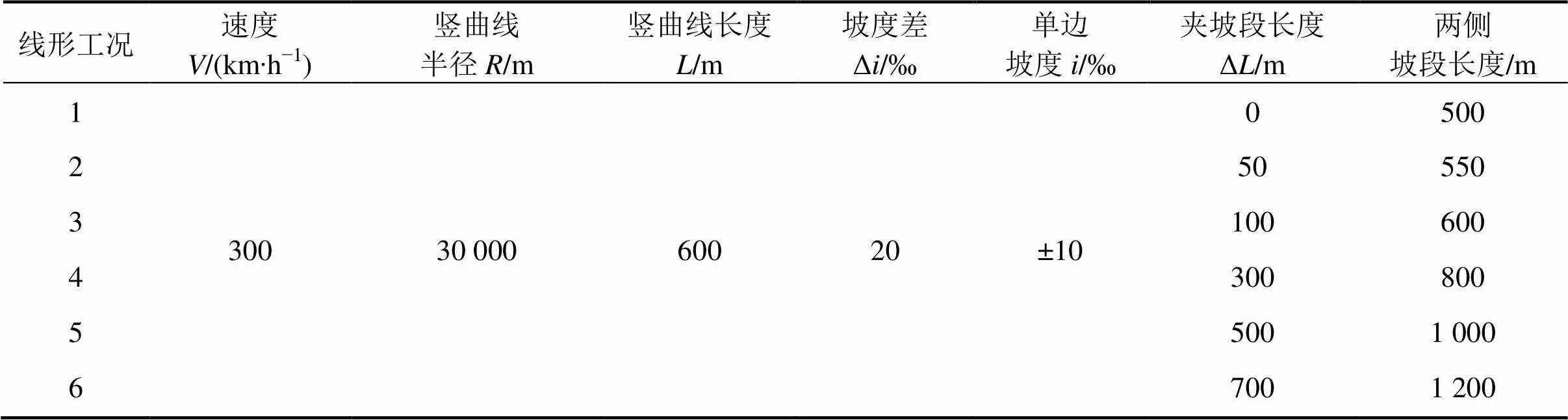
表5 不同夹坡段长度下的线形工况
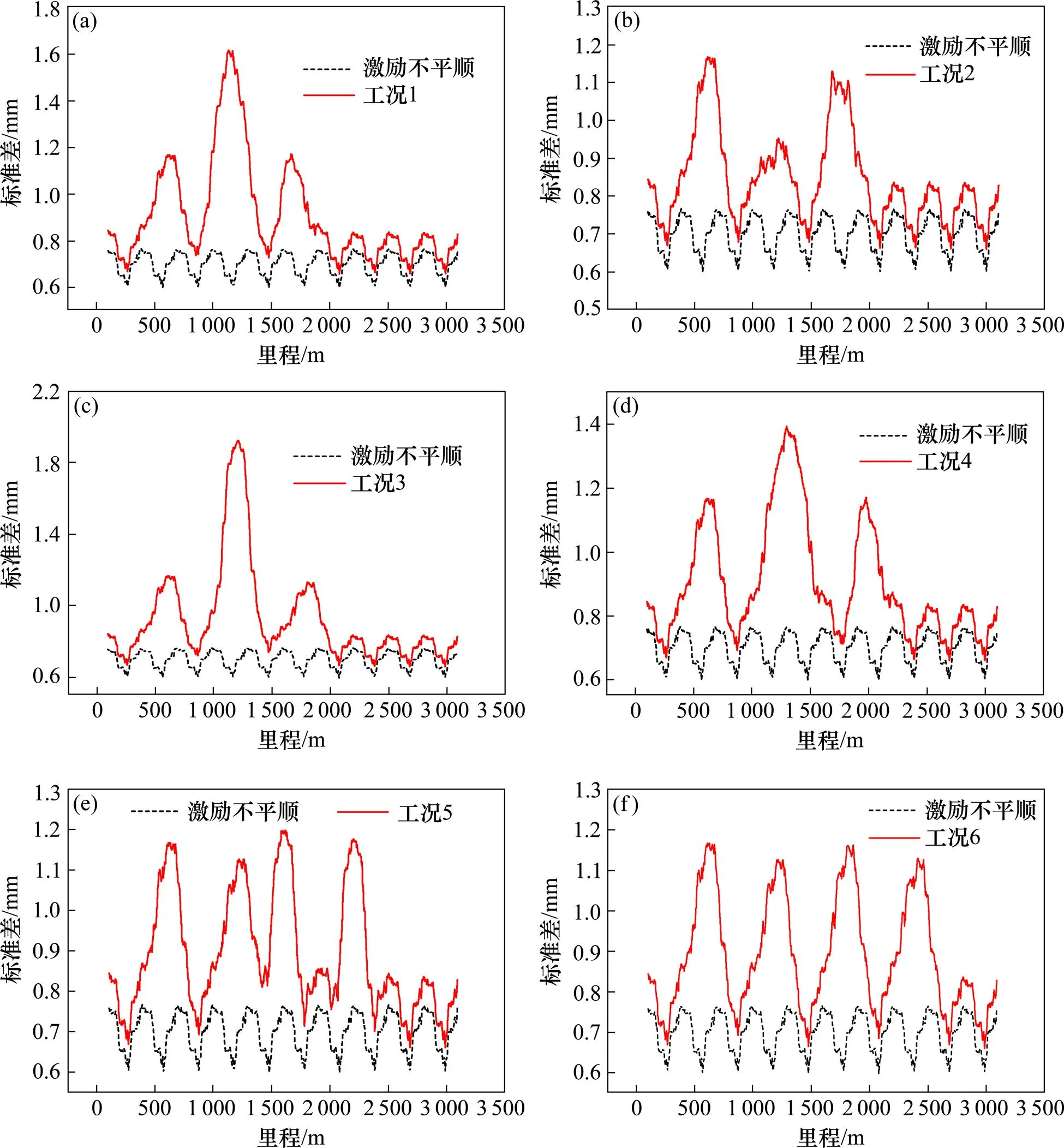
(a) 工况1;(b) 工况2;(c) 工况3;(d) 工况4;(e) 工况5;(f) 工况6
由图9可知,当夹坡段长度小于500 m时,虚拟不平顺的标准差曲线仅有3个“驼峰”,即前一段竖曲线的圆直点与后一段竖曲线直圆点引起的虚拟不平顺会相互影响并且叠加。而当夹坡段长度大于500 m后,前一段竖曲线和后一段竖曲线之间的影响逐渐减弱,叠加效应基本消失。
将5种工况对比可知,5种工况下峰1不受叠加效应的影响故里程和峰值均较平稳,基本稳定在610 m和1.17 mm左右;峰2的里程基本稳定在 1 200 m左右,但标准差值在夹坡段长度小于500 m时由于2段竖曲线的叠加效应导致波动较随机,在大于500 m后标准差基本稳定在1.17 mm左右;峰3的里程基本随夹坡段的长度增加而增加,但标准差不受叠加效应的影响基本稳定在1.17 mm左右;峰4在夹坡段长度大于500 m后出现,但里程和标准差值规律同峰3。
不同夹坡段长度下虚拟不平顺与激励不平顺的频域对比见图10。
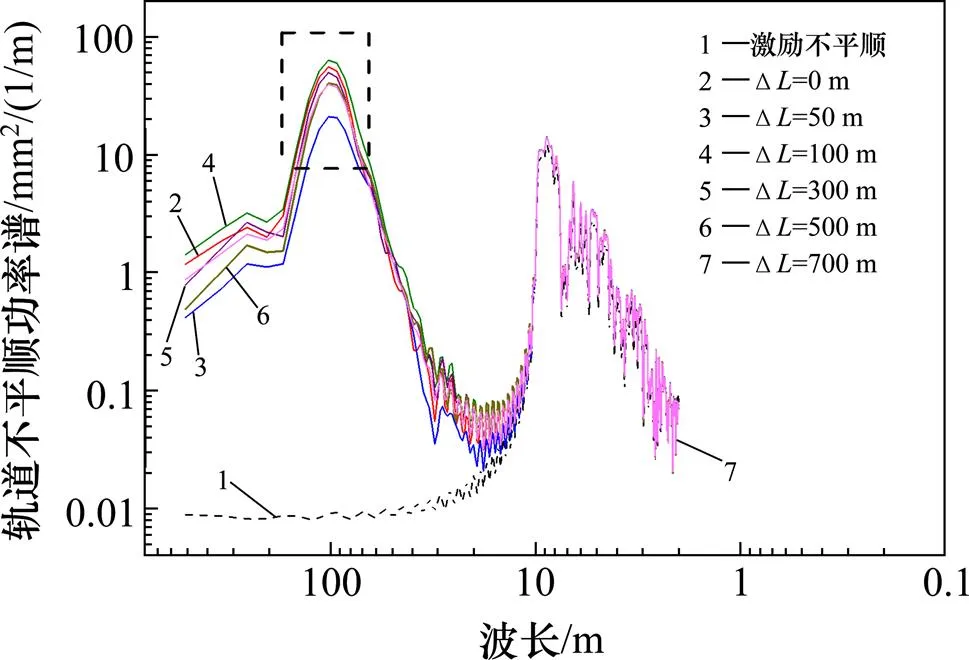
图10 不同夹坡段长度下的虚拟与激励不平顺轨道谱对比
由图10可知,不同夹坡段长度工况下虚拟不平顺的轨道谱曲线与上几节基本相同,长波长主要稳定在102.4 m,但功率谱密度值在夹坡段长度较短时由于叠加效应数值有较大波动,但在夹坡段长度大于500 m后,如上图右所示其数值则基本稳定在40 mm2/(1/m)。
综上可知,当夹坡段长度满足不叠加的要求(大于500 m)后,夹坡段长度不是影响虚拟不平顺的主要因素,即夹坡段长度对纵断面线形的平顺性影响较小。将所得结果与规范对比,规范中规定2竖曲线间的最小夹坡段长度不得小于0.4max,即120 m,由此可知规范要求较宽松,为保证竖曲线设计时不产生初始不平顺,本文建议:对于设计时速为300 km/h的高速铁路,在设计夹坡段长度时需保证大于500 m。
3 结论
1) 通过分析可知,各参数对纵断面线形平顺性的主要影响位置为竖曲线的直圆点和圆直点处,且不同参数对平顺性的影响不同。
2) 列车检测速度和竖曲线半径是影响虚拟不平顺的主要因素,且不同检测速度会影响虚拟不平顺的长波成分。
3) 竖曲线长度和夹坡段长度在满足不叠加要求(长度大于500 m,夹坡段大于500 m)后基本对虚拟不平顺不产生影响,但为防止竖曲线设计时产生初始不平顺,本文建议:对于设计时速为300 km/h的高速铁路,这2个因素除满足规范中大于25 m和0.4max的要求外,在设计允许的情况下应保证其取值均大于500 m。
[1] 练松良, 黄俊飞. 客货共运线路轨道不平顺不利波长的分析研究[J]. 铁道学报, 2004, 26(2): 111−115. LIAN Songliang, HUANG Junfei. Study of the detrimental wavelengths of track irregularities for railways with passenger and freight traffic[J]. Journal of the China Railway Society, 2004, 26(2): 111−115.
[2] XU P, LIU R, SUN Q, et al. A novel short-range prediction model for railway track irregularity[J]. Discrete Dynamics in Nature and Society, 2012: 1951− 1965.
[3] 翁绍德, 罗林. 法铁线路保持平顺稳定的技术和经验——考察法铁线路的心得体会[J]. 铁道建筑, 1991(1): 3−8. WEN Shaode, LUO Lin. Technology and experience to maintain railway smooth and stable-the experience of investigating the French railway[J]. Railway Engineering, 1991(1): 3−8.
[4] 吴晓峰.杭长高铁长波高低不平顺问题的研究与分析[J].上海铁道科技, 2015(3): 8−9, 19. WU Xiaofeng. Research and analysis on the problem of vertical long wave irregularity in Hang-Chang high-speed railway[J]. Shanghai Railway Science & Technology, 2015(3): 8−9, 19.
[5] 王海涌, 党建武, 王晓明. 基于舒适度的高速铁路线路设计与优化[J]. 铁道工程学报, 2014, 31(11): 30−34. WANG Haiyong, DANG Jianwu, WANG Xiaoming. Design and optimization of high-speed railway lines based on comfort[J]. Journal of Railway Engineering Society, 2014, 31(11): 30−34.
[6] 龙许友, 时瑾, 方文珊. 高速铁路纵断面设置对乘坐舒适性影响评价[J]. 铁道工程学报, 2015(4): 48−53. LONG Xuyoutyou, SHI Jin, FANG Wenshan. Evaluation of ride comfort caused by track vertical alignment of high-speed railway[J]. Journal of Railway Engineering Society, 2015(4): 48−53.
[7] 王海涌, 党建武, 王晓明. 基于线路参数的高速铁路乘坐舒适度评价方法研究[J]. 兰州交通大学学报, 2015, 34(4): 53−56. WANG Haiyong, DANG Jianwu, WANG Xiaoming. Evaluation of the comfort of high-speed trains based on line parameters[J]. Journal of Lanzhou Jiaotong University, 2015, 34(4): 53−56.
[8] 李向国. 高速铁路线路参数分析及其行车动力特性研究[D]. 成都: 西南交通大学, 2011. LI Xiangguo. Study on alignment parameter and its vehicle dynamic behavior for high-speed railways[D]. Chengdu: Southwest Jiaotong University, 2011.
[9] 申雄. 高速客运专线纵断面设计参数对车线动力响应影响研究[D]. 北京: 北京交通大学, 2012. SHEN Xiong.The study on effect of profile parameter on high speed passenger railway dynamic response[D]. Beijing: Beijing Jiaotong University, 2012.
[10] 周劲松. 铁道车辆振动与控制[M]. 北京: 中国铁道出版社, 2012. ZHOU Jinsong. Railway vehicle vibration and control[M]. Beijing: China Raillway Press, 2012.
[11] Matsumoto H M, Harada Y. Application of axle-box acceleration to track condition monitoring for rail corrugation management[C]// Railway Condition Monitoring, IET, 2017.
[12] WANG Y, QIN Y, WEI X. Track irregularities estimation based on acceleration measurements[C]// International Conference on Measurement, Information and Control, IEEE, 2012: 83−87.
[13] Proakis J G, Manolakis D G. Digital signal processing: principles, algorithms, and applications[M]. 3rd ed. Prentice-Hall, 1996.
[14] 李成辉. 高底不平顺不利波长及其与车速关系[J]. 西南交通大学学报, 1997, 32(6): 61−64. LI Chenghui. Relationship between irregular wavelength of tracks and vehicle speed[J]. Journal of Southwest Jiaotong University, 1997, 32(6): 61−64.
[15] TB10621—2014, 高速铁路设计规范[S]. TB10621—2014, Code for desigh of high speed railway [S].
(编辑 阳丽霞)
Study on profile line regularity based on the inertial reference method in high-speed railway
LI Shuai1, YI Yangming2, WANG Yuan1, CHEN Rong1, WANG Ping1
(1. Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Chengdu Railway Bureau, Chengdu 610031, China)
In order to research on the transfinite problem of long-wave irregularity caused by the vertical curve, this paper used the virtual track inspection technology based on inertial reference method. The high-speed train-line dynamics simulation model was established, and the virtual irregularity was obtained through the inversion of body acceleration and body-wheel relative displacement. The influence of parameters like train detection speed, radius and length of vertical curve, gradient difference and clip slope length on the virtual irregularity was investigated. The analysis results show that the detection speed and radius of vertical curve have big influence on virtual long wave irregularity. Through the comparison between the calculated results and specification, this paper suggests that for design speed of 300 km/h in high-speed railway, under design permission the design value of vertical curve length and clip slope length should be greater than 500 m.
high-speed railway; inertial reference method; virtual track inspection technology; line profile; long wave irregularity
10.19713/j.cnki.43−1423/u.2018.08.001
U212.34
A
1672 − 7029(2018)08 − 1901 − 10
2017−06−28
国家杰出青年科学基金资助项目(51425804);中国铁路总公司科研项目(2015G002-A);南昌铁路局科研开发项目(201627)
陈嵘(1981−),男,湖南衡阳人,教授,博士,从事高速重载轨道结构及轨道动力学研究;E−mail:chenrong@home.swjtu.edu.cn

