基于3PLM和GRM混合模型的等值方法比较

黎光明

（华南师范大学心理学院、心理应用研究中心，广州 510631）

1 引言

等值是心理与教育测量领域的一个重要组成部分，是测验标准化过程中的一个必备程序（漆书青，戴海崎，丁树良，2002）。具体而言，测验等值是指将测量同一心理品质的多个测验形式上的测验分数或项目参数的单位系统进行转换，以达到相互间对应指标可比的过程。进行等值处理后，同一考生在不同测验版本上的得分相同。一般来说，进行等值必须满足四个前提条件，即同质性、等价性、样本一致性及对称性（张敏强，1998）。

在题库的建设中，项目参数估计和等值是两个突出的技术问题。传统的基于经典测量理论的等值方法只能实现不同试卷之间的等值，而随着项目反应理论（Item Response Theory，IRT）在心理与教育测量领域越来越广泛的应用 （黎光明，张敏强，2012），基于IRT的等值方法实现了将试题的难度、区分度、猜测水平等题目参数置于同一尺度上，从而满足大规模题库建设的需要。

按照项目反应理论，同一项目在不同的单位系统上虽然参数值的数字表现形式不同，但实质却一样。假设有两个测验X和Y，且两测验有M个锚题，同一项目的两套参数间必然存在如下的线性转换关系 （Sayaka ＆ Shinichi，2011； Kolen ＆ Brennan，2013）：

在公式（1）～（4）中，A 和 B 为线性转换参数（等值常数），θxi，axj，bxj，cxj表示在群体 x 上估计出的参数，θyi，ayj，byj，cyj为在群体 y 上估计出的参数。除非另外有申明，一般假设 i＝1，2，…，N；j＝1，2，…，M。

上述这些公式反映了在项目反应理论模型下，不同单位系统的各种参数之间的等值转换模式，A和B为等值转换系数。

在项目反应理论的指导下，研究者建立了众多的计量模型，这些模型都有各自的特点和所适用的范围。在实际的应用过程中，研究者往往会根据情况进行选择以达到模型对数据的最佳拟合。在实际的研究工作中我们常常会遇到一份测验材料既有0－1评分的多重选择题 （Multiple－Choice items，MC）又有多级评分的简答题或解答题（Construct－Response items，CR）的情况。传统的做法通常是选用多级评分模型，因为0－1计分是多级评分的一个特例。但是，该做法忽略了0－1计分题目中的猜测行为，使得分析结果的准确性和科学性受到了影响 （张敏强，黎光明，王小婷，黄春汝，王幸君，2015）。事实上，在这种情况下应该考虑“混合模型”，即0－1计分的试题选用0－1计分模型，多级评分的试题选用多级评分模型，两个模型结合共同完成对测试材料的分析（周世科，2008）。“混合模型”是指测验分数中既包含有二级记分题型，又包含多级记分题型的混合题型，需要用不同的项目反应理论模型来区别对待的模型。“混合模型”在参数估计过程中，所有参数均是同时估计的。

目前关于“混合模型”各方面的研究并不多。国外对于混合题型测验等值的研究大多仅采用MC作为锚题，主要是因为当MC和CR得分相关高、锚题得分和总分相关高、MC占得分值比例高及被试能力水平差异小时，得到的等值精度更高。也就是说，为了追求较高的等值精度，CR题型的数量和所占的分值要尽可能少。但是，Tate（2000）指出仅采用MC题型作为锚题会产生大的等值误差。另外，Tate也认为，锚题仅包含MC题目也并不符合锚题为原测验的 “缩影”这一原则，不具备代表性。

国外也有少量的研究将MC和CR共同作为锚题来进行混合题型测验的等值。Tian（2011）对混合题型测验的等值进行了模拟研究，比较了仅用MC项目作为锚题、仅用CR项目作为锚题以及用MC和CR项目共同作为锚题这三种不同的锚题题型设置情况，结果发现同时参数标定比SLcrit法的等值在三种不同的锚题题型设置情况下精确性都更高。Kim 和 Lee（2006）也进行了基于 3PLM（Three－Parameter Logistic Model）和 GPCM（Generalized Partial Credit Model）混合模型下的研究，结果得出特征曲线法要优于矩估计法，而Habera法又略优于SL法。实际上，基于3PLM和GPCM混合模型比较还受到其它因素影响，如题目数量、记分模型等。Saen－amnuaiphon， Tuksino 和 NIchanong （2012）认为，在3PLM和GPCM混合模型下CR项目数量比MC项目数量越多，测验信息量越大，测验越有效。Kim 和 Walker（2012）认为，在锚题为 MC 和 CR时对模型选择进行比较，仅采用多级记分模型的等值误差很大。

而对于混合题型的等值研究，国内仅有周世科（2008）对此进行了专门研究，采用的是测验特征曲线法，比较了混合模型和GRM （Graded Response Model）模型对混合题型的等值精度。结果得出锚题为混合题型时，仅采用多级计分模型误差会增大，采用混合模型会比仅用GRM更适合。特征曲线法是一种项目参数等值方法，而GRM是一种IRT数学模型。涂冬波、蔡艳、戴海琦和丁树良（2011）也认同一个模型往往很难反映所有数据资料本身的特点，可考虑应用多个IRT模型（即混合模型）来分析，以达到对数据的最佳拟合，并对基于3PLM和GRM的混合模型的思想方法及原理、参数估计的实现以及模型性能进行了研究。

综合前人在相关领域的研究结果，本研究着重讨论基于3PLM和GRM的混合模型下的多种IRT等值方法，并比较它们的性能优劣，以期为相关理论研究和实际应用提供参考。

2 研究方法

2.1 数据来源

数据来源为广东省佛山市 “升中”考试实测数据，分为“课改实验区”和“非课改实验区”。“升中”数学考试相应地分为课改区的测验X和非课改区的测验Y。从课改区和非课改区随机各抽取10000人。测验X和测验Y各有24道题，其中客观题15道，主观题9道。测验X和测验Y有一个锚测验V，测验V的主客观题共9道题。

2.2 等值设计与方法

由于课改区与非课改区考生的能力有所差异，且课改区和非课改区的测验中有共用的锚题，因此本研究采用非等组锚测验设计。等值方法选用平均数－平均数法（Mean／Mean Method，MM）、平均数－标准差法（Mean／Sigma Method，MS）、稳健的平均数－标准差法（Robust Mean and Sigma Method，RMS）、Haebara法（HA）以及 Stocking－Lord 法（SL）。

2.3 等值步骤

2.3.1 参数估计

依据3PLM和GRM的混合模型分别对混合题型的测验X和测验Y进行参数估计。其中，依据3PLM模型分别对两测验的客观题进行参数估计，依据GRM模型分别对两测验的主观题进行参数估计。所使用的参数估计软件是Parscale4.1。

2.3.2 测验等值

分别将混合题型、只有客观题以及只有主观题的测验X和测验Y通过IRTEQ进行等值转换，得到以下三种结果：一是3PLM和GRM混合模型下五种等值方法的混合题型测验观察分数等值结果、二是3PLM模型下五种等值方法的客观题测验观察分数等值结果、三是GRM模型下五种等值方法的主观题测验观察分数等值结果。

2.3.3 数据分析

使用软件SPSS19.0对等值的结果进行方差分析。

2.4 比较基准和标准

2.4.1 比较基准

模拟研究中可以设置测验项目的指标，然而实证研究在现实中往往是无法设置测验项目的真实指标。 在 Lord （1977）、Marco 等人 （1979）、谢小庆（2000）、焦丽亚和辛涛等人（2006）的研究中，经典测量理论（Classical Test Theory， CTT）中的 Tucker线性等值方法都是比较出色的。因此，本研究选用CTT等值方法中的Tucker线性等值结果作为五种IRT等值方法的分数等值的比较基准。

2.4.2 比较标准

五种IRT等值方法观察分数的比较标准是计算这五种IRT等值方法测验观察分数等值结果与作为比较基准的Tucker等值观察分数等值结果的两种差异量 （谢小庆，2000；黎光明，张敏强，2012； Kang ＆ Petersen， 2012）：

一是误差平均差，用于方差分析，观察题型与等值方法之间是否存在交互作用。误差平均差由下式定义：

在公式 （5）中，m为测验的题目数，j是原始分数，t'm是作为评价标准，tm是估计的等值分是原始分数对应的五种IRT等值方法结果与作为评价标准的等值分相减后所得的平均误差。

二是标准加权均方差或总误差的平方根，用于对混合模型下五种IRT等值方法结果的精确性排名。总误差平方根由下式定义：

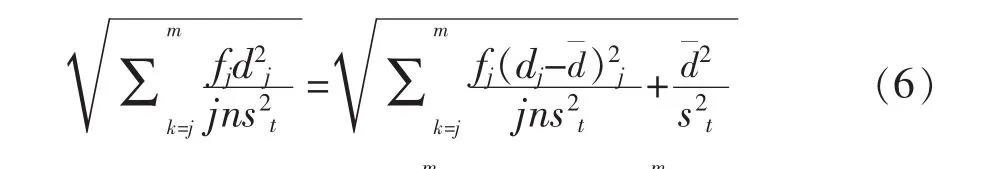
3 结果与分析

3.1 测验观察分数等值结果

五种IRT等值方法下的混合题型、客观题以及主观题测验观察分数部分等值结果及作为评价标准的Tucker观察分数部分等值结果列于表1～表3。

3.2 误差平均差的方差分析

根据误差平均差的定义，分别计算五种等值方法结果误差平均差，并把所得的误差平均差作为因变量，五种IRT等值法和题型作为自变量，进行两因素方差分析，描述统计结果如表4所示。

表4是五种等值法与三种题型条件下的描述统计，其平均数M是根据公式（5）求取的，标准差是根据每个绝对离差值计算得到的，主要为了反映绝对离差值的离散趋势。

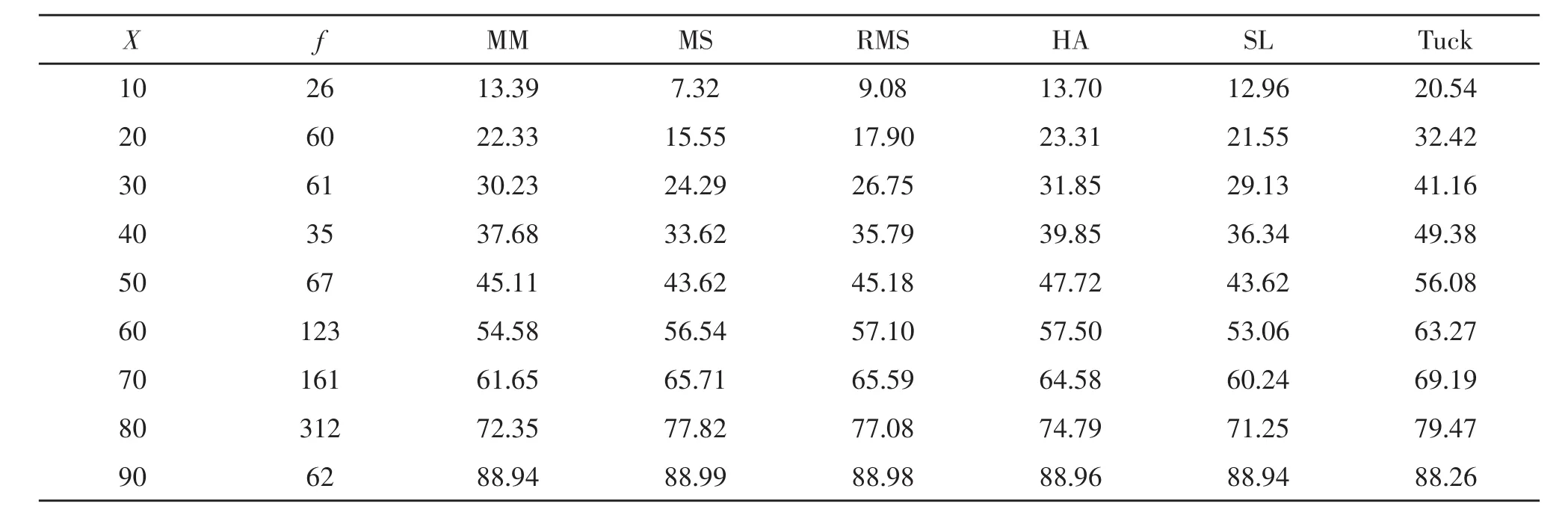
表1 五种IRT等值方法下的混合题型测验观察分数等值结果

表2 五种IRT等值方法下的客观题测验观察分数等值结果

对五种IRT等值方法测验观察分数等值进行方差分析，结果如表5所示。

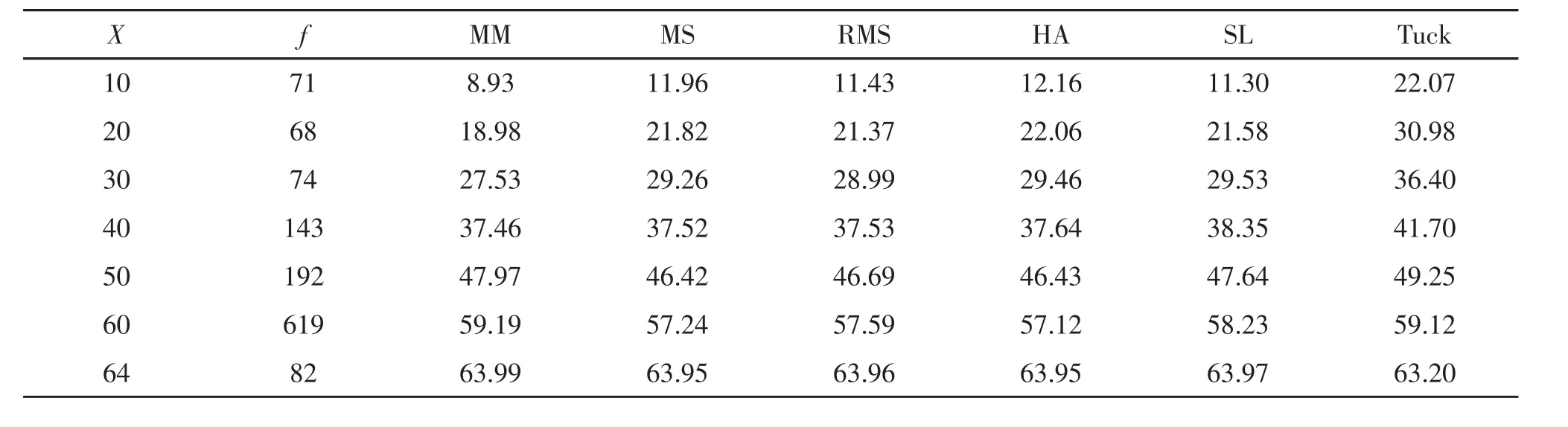
表3 五种IRT等值方法下的主观题测验观察分数等值结果

表4 五种等值法与3种题型条件下的描述统计

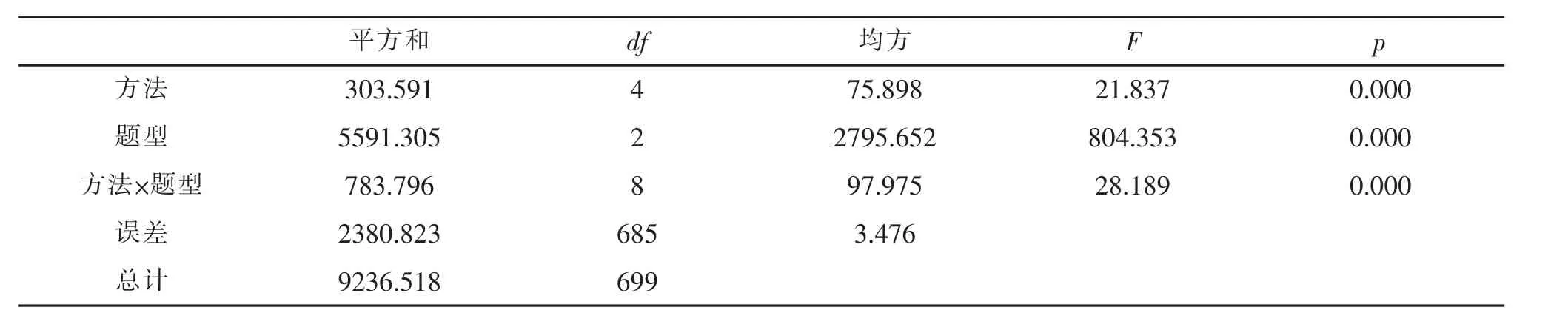
表5 五种等值法与三种题型条件下方差分析的主效应检验

从表5可知，五种IRT等值方法的主效应显著，F（4，660）＝21.837，p＜0.001；题型的主效应显著 F（2，660）＝804.353，p＜0.001；两因素间的交互作用也显著 F（8，660）＝97.975，p＜0.001。 因此，需要进一步作事后检验。

多重比较分析后发现，五种IRT等值方法中，HA法与MS、RMS这两种方法差异显著 （p＜0.001；p＜0.001），且HA法的误差最小，而与 MM 法和 SL法的差异并不显著（p＝0.097；p＝0.429）；同时，HL 法与MS、RMS这两种方法的差异也是显著的（p＜0.05；p＜0.05），且SL法的误差比较小，但SL法与MM法差异并不显著（p＝0.997）；其他的情况包括，MM 法与MS法、MM法与RMS法、MS法与RMS法，结果显示差异均不显著（p＝0.129；p＝0.278；p＝1.000）。

而在客观题、主观题、混合题型中，客观题与主观题的差异显著（p＜0.001），与混合题型的差异也显著 （p＜0.001），且客观题的误差要小于另外两种题型；主观题与混合题型间差异也显著（p＜0.05），且混合题型误差小于主观题。

从表5还能看出，IRT方法与题型的交互作用显著，作进一步简单效应检验后发现，在题型因素下，各种IRT方法在只有客观题时的差异不显著，而在主观题和混合题型中都有显著差异。具体地，客观题时 F（4，699）＝1.30，p＝0.270；主观题时 F（4，699）＝3.39，p＜0.05；混合题型时 F（4，699）＝22.55，p＜0.001。3.3 混合题型下总误差平方根比较结果

混合题型下总误差平方根比较结果如表6所示。表6是五种等值法的总误差平方根，是根据公式（6）求取的，主要反映总误差的相对大小。

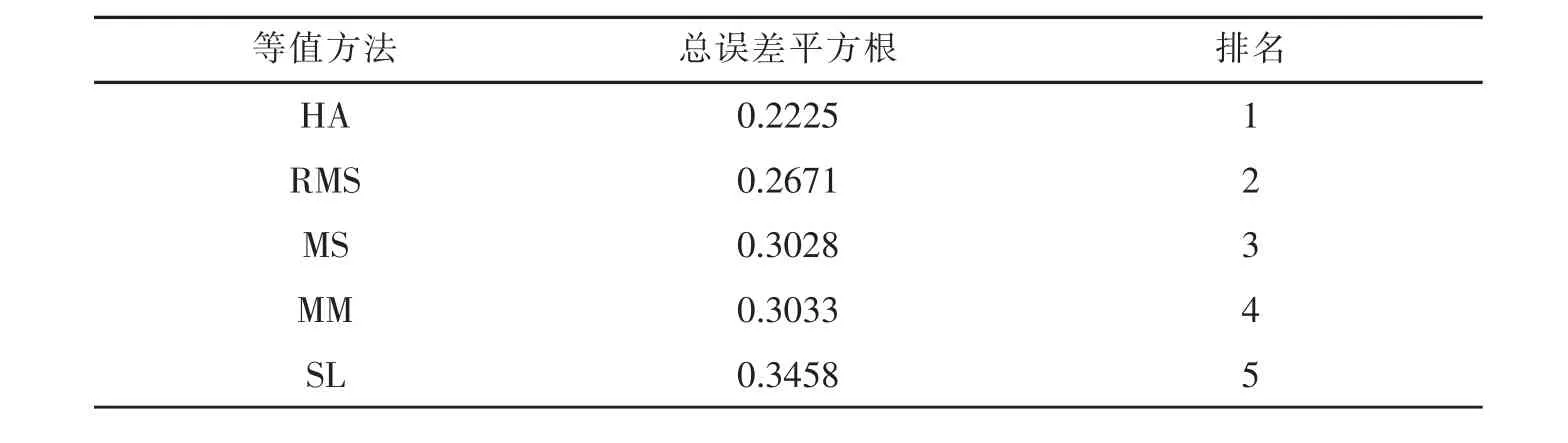
表6 五种方法的等值结果比较

从表6可以看出，Haebara特征曲线法 （HA）最为精确，其次是稳健的MS方法（RMS），再次是MS法，MM 方法列第四，而 Stocking－Lord 法（SL）的等值误差最大。?

4 讨论

本研究采用非随机锚测验设计，选用3PLM和GRM的混合模型对数据进行测验等值。本研究之所以选用非随机锚测验设计，是因为测验X和测验Y有共同锚题。锚题数量有9道，总题量共24道，占37.5%；锚题分值为39分，总分值为89分，锚题分值占总分值约为44%；锚题题型既有二级记分，也有多级记分，这表明锚测验设计是科学的，符合锚测验是原测验的“缩影”这一要求，具备代表性。

测验X与测验Y都是混合题型测验，即既有客观题也有主观题，其中客观题数量是15题，占总题量62.5%，分值为25分，占总分28.1%；主观题数量是9题，占总题量37.5%，分值为64分，占总分71.9%。由于不同的题型拟合不同的模型，所以本研究选取了3PLM和GRM混合模型，对于0－1评分项目用3PLM模型，多级评分项目用GRM模型。本研究选用3PLM和GRM的混合模型对数据进行测验等值，是因为这样做能够使得模型达到对数据的最佳拟合。

从表5的结果可知，在三种题型中，客观题的误差平均差值最小，优于混合题型和主观题，而混合题又优于主观题。但是，由于客观题本身的分值较小，等值后其分数误差可浮动的范围并不大，所以使得在只有客观题的情况下，其等值后的误差平均差值相对较小。因此，当测验中只有客观题时，采用IRT方法进行等值的结果要比含有主观题时更加精确。但是，应该注意的是，这并不表示只有客观题的测验的等值结果才最能反映被试的真实水平。事实上，最能反映被试真实水平并具有现实意义的测验是混合题型，这里所反映的仅仅只是等值结果的精确性。

从表5的方差分析结果来看，五种IRT方法的主效应是显著的。从进一步的事后检验的可以看出，HA法与SL法的等值效果最优；其次是MM法；最后是RMS法与MS法。其中，HA法与RMS法、MS法之间存在着显著性差异；SL法与RMS法和MS法之间也存在着显著性差异；而其他方法间并未发现显著的差异。

从表6的结果可以看出，以标准加权均方差为比较标准时，根据总标准加权均方差或总误差平方根值越小测验等值误差越小的原则，可以发现HA法最佳（排名第一），其次是RMS法（排名第二），再次是MS法和MM法（分别排名第三和第四），最差是SL法（排名第五）。

评价指标的选取也是一个问题，选取不同的评价指标可能会得出不一样的结果。为增加结果的可信度，本研究同时采用了两种等值比较的评价指标。综合各研究结果来看，因为等值结果的比较在标准加权均方差和误差平均差两种比较标准中并不太一致，即SL法在选用误差平均差作为评价指标时表现较好，而选用标准加权均方差作为评价指标时表现是最差的。这很可能就说明了两种比较标准结果可能是并不一致的。但是，HA法在两种评价指标中都是误差最小的。因此，可以认为五种IRT等值方法中，HA法是最优的，有着很大的等值优势。

评价比较不同等值方法精确性的参照标准问题正是等值研究中一直没有得以有效解决的一个重要问题。本研究选用Tucker等值方法作为检验标准是因为国内外许多等值方法的比较研究（Lord，1977；Marco， Petersen， ＆ Stewart，1979； 焦丽亚， 辛涛，2006；谢小庆，2000）均显示出Tucker方法相对于其他很多方法准确性是比较高的，另外也有很多研究以Tucker方法作为检验标准。但是，选用Tucker方法作为标准只能用等值分计算等值误差作为评价的指标，这样便会忽略了IRT理论采用各项目参数的优势。有关等值研究的已有文献（丁树良，熊建华，戴海琦，2005；焦丽亚，辛涛，2009）表明，许多关于等值方法的比较研究并没有达成一致的结果，最主要的一个原因为实践中缺少一个评价等值方法精确性和有效的绝对标准。

在今后的研究中，为有效解决评价标准等方面的问题，可以开展进一步的模拟研究。原因在于，当使用真实数据时，没有很好的评价构建共同尺度的方法。因为不存在评价结果精确性的标准，只有在两套项目参数的关系已知时，才可以完成评价，这样的标准只有在模拟数据的情况下存在。

5 结论

IRT五种等值方法中，Haebara特征曲线法（HA）最优。即便评价指标不一致，但无论是选取误差平均差，还是选取标准加权均方差作为评价指标时，HA法都是误差最小的方法。

客观题等值结果最为精确，主观题等值误差最大，包括客观题与主观题的混合题的等值误差介于两者之间。

等值方法与题型具有交互作用，客观题等值方法间差异不显著，而主观题或混合题等值方法间出现显著差异。