复合材料薄板斜接式挖补修理稳定性优化设计

卢俊文 麦海波 张殊伦

(中国民用航空飞行学院，广汉 618307)

0 引言

为了减少机身结构质量，复合材料薄板结构在飞机上应用日趋广泛，薄板结构在承受载荷时很容易出现失稳现象。为了确保复合材料结构具有高的稳定性，近几年来各国研究人员进行了大量的复合材料结构稳定性优化研究[1-7]，但对复合材料薄板斜接式挖补修理结构的失稳载荷影响因素的优化研究甚少。随着轻型全复合材料航空器大量投入使用以及飞机使用率的大幅度提升，挖补修理已经成为了复合材料薄板结构的最重要修理方式之一，其修理稳定性优化研究变的尤为重要。

本文使用商用有限元软件ANSYS对经过挖补后的复合材料薄板结构的失稳载荷进行了优化分析，考虑了挖补角、胶层厚度、补片材料与母板材料匹配对挖补修理层合板结构失稳载荷的影响，为复合材料层合板结构的挖补修理技术提供了一定的理论指导。

1 挖补修理模型描述

1.1 挖补参数说明

由于挖补铺层方式对挖补修理稳定性的影响在文献[8]中进行了详细研究，在本优化过程中未进行详细研究，考虑了同种材料以及异种材料的挖补修理匹配，考虑了挖补角、胶层厚度对稳定性的影响。具体参数见表1。

表1 材料性能参数

1.2 挖补修理结构

考虑到结构与边界条件的对称性，此处只需要建立挖补修理结构的1/4模型，结构参数、边界条件、载荷施加如图1所示。母板与补片通过粘接的方式连接在一起，粘接形式为斜接，母板材料与补片材料均为4种，分别是碳纤维、玻璃纤维、石墨纤维和硼纤维层合板，进行自由组合后进行挖补稳定性优化分析，胶层材料为SY-14面-面胶黏剂[9-10]。母板与补片的铺层方式如表2所示，均为[±45/90/02/±45/0]s，该挖补修理机构中层合板单层厚度为0.125 mm。

图1 挖补修理模型结构Fig.1 Scarf repair model

2 复合材料层合板稳定性计算理论

假设一块各向异性的复合材料薄板的长度为a，宽度为b，厚度为h。考虑到材料的各向异性，假设板的厚度为均厚，其控制方程见公式(1)[9]。

(1)

式中,Dij为薄板的弹性刚度矩阵，σx,σy，σxy分别为板内应力分量。

对于一端固定约束的复合材料薄板，其约束方程见式(2)。

或者

(2)

(3)

(4)

公式(4)中，Qij(i,j=1,2,6)由公式(5)来计算。

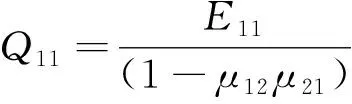
(5)

式中，E11为第一方向上的弹性模量，E22为第二方向上的弹性模量，G12为剪切模量，μ12和μ21分别为泊松比，他们之间的关系见公式(6)。

(6)

最后通过矩阵计算简化后得出求解失稳载荷的方程：

([K]+λ[S]){ψ}=0

(7)

式中，[K]表示结构刚度矩阵，[S]为初始应力刚度矩阵，﹛ψ﹜为位移特征值矢量，λ为失稳载荷。

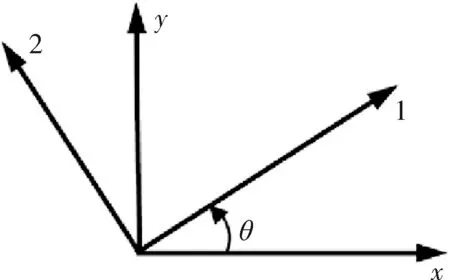
图2 坐标参考图Fig.2 Coordinate reference

3 优化分析

3.1 优化分析实现

本优化设计是通过不同材料的母板与补片匹配、胶层厚度以及挖补角三个因素来实现挖补修理结构稳定性最优化，属于单目标优化，采用ANSYS中“optiSLang”优化插件调用APDL程序中参数来实现，采用“optiSLang”优化插件中的自适应响应面法(Adaptive Response Surface Method，简称ARSM)。可以通过f(x1，x2，...，xk)→max来表述。

在本优化中，其中胶层厚度、挖补角通过“optiSLang”优化插件来实现自动优化，母板材料与补片材料的匹配是通过修改APDL程序中的材料参数匹配来实现。

3.2 优化分析流程

在整个优化过程中，四种材料的层合板自由搭配，涉及16种补片与母板搭配方案，调用了16个APDL程序，每一种方案的优化过程中产生的优化点在20～90个左右，不同材料匹配模型的优化点数不同。具体的优化方案见图3，流程见图4。首先确定输入参数的初始设计范围(Design of Experiments，简称DOE)，在满足实际修理可行的前提下，这里规定胶层厚度范围为0.1～0.6 mm，挖补角范围为3°～60°。然后采用ARSM算法，经过前期几个设计点计算，ARSM算法会自动缩小DOE范围，可以很快地逼近最优解。

图3 优化方案图Fig.3 Optimization scheme

图4 优化流程图Fig.4 Circuit of optimization

4 优化结果分析

通过对挖补修理结构的稳定性优化分析，得出了结构在4种母板材料下，结构最优失稳载荷随着补片材料、挖补角、胶层厚度的变化情况，并做了比较与分析，如图5～图8所示。

图5 基体材料为玻璃纤维层合板的挖补修理失稳载荷变化图Fig.5 Instability loads for scarf repaired glass fiber laminates

图6 基体材料为硼纤维层合板的挖补修理失稳载荷变化图Fig.6 Instability loads for scarf repaired boron fiber laminates

图7 基体材料为石墨纤维层合板的挖补修理失稳载荷变化图Fig.7 Instability loads for scarf repaired graphite fiber laminates

图8 基体材料为碳纤维层合板的挖补修理失稳载荷变化图Fig.8 Instability loads for scarf repaired carbon fiber laminates

对于玻璃纤维复合材料层合板挖补修理，最优挖补修理方案为：胶层厚度0.481 mm，挖补角为5°，补片材料为硼纤维层合板，失稳载荷可以达到3.355 MPa。

对于硼纤维复合材料层合板挖补修理，最优挖补修理方案为：胶层厚度0.457 mm，挖补角为60°，补片材料为硼纤维层合板，失稳载荷可以达到7.067 MPa。

对于石墨纤维复合材料层合板挖补修理，最优挖补修理方案为：胶层厚度0.111 mm，挖补角为13°，补片材料为硼纤维层合板，失稳载荷可以达到5.579 MPa。

对于碳纤维复合材料层合板挖补修理，最优挖补修理方案为：胶层厚度0.450 mm，挖补角为4°，补片材料为硼纤维层合板，失稳载荷可以达到4.975 MPa。

分析上面数据得出以下结论：

4种挖补修理的最优方案，补片材料的本身的弹性与剪切模量的大小对挖补修理的稳定性影响最大，通过优化计算得出硼纤维层合板的6个方向上模量搭配最优，硼纤维层合板补片明显增强了挖补修理结构的稳定性。

对于母板为硼纤维层合板挖补修理结构，胶层厚度和挖补角均大于其他修理方案，这与硼纤维层合板本身的模量特性有关。对于母板为玻璃纤维、石墨纤维层合板挖补修理结构，经过一定周期的优化计算后，很快趋于最优解附近。对于碳-碳挖补修理结构，结构稳定性受胶层厚度影响很大，随着胶层厚度的增加，失稳载荷很快地近线性减小。对于硼-碳挖补修理结构，失稳载荷随着胶层厚度的增加，很快地近线性增大。

5 结论

经过斜接式挖补修理层合板的稳定性优化分析，研究了补片材料、挖补角、胶层厚度与挖补修理结构失稳载荷的关系，同时得出了理论最优的挖补修理模型。下面进行分析结果的总结：

(1)补片材料的各方向上的模量特性对挖补修理结构稳定性影响显著，各个方向上模量的增大在一定范围内会明显提高挖补修理结构的稳定性。

(2)ARSM优化算法可以很好地适用于两参数的挖补修理稳定性优化分析，同时很快地搜索出最优修理方案。

(3)胶层厚度与挖补角对挖补修理结构稳定性的影响与补片和母板材料有着密切的联系，材料不同，造成的影响不同。

通过有限元与ARSM相结合的优化方法，可以很方便的实现挖补修理结构稳定性的优化。下面对今后的研究提出一些展望：

(1)需要进一步研究补片材料的各个模量参数对挖补修理稳定性影响的机理。

(2)需要将补片形状参数考虑进来，研究补片形状对挖补修理结构稳定性的影响，并实现补片形状优化。

(3)需要进一步探明胶层厚度、挖补角与挖补修理结构中材料模量特性的关系。