一种改进的基于“当前”统计模型的联合概率数据关联算法

魏 祥，李 颖，骆荣剑

（陆军工程大学通信士官学校，湖北 武汉 430000）

“当前”统计模型作为处理机动目标的重要方法之一，在目标处于机动状态下，利用该算法对目标进行跟踪一直是该领域的研究热点，“当前”统计模型采用非零均值的时间相关模型，该模型相对Singer模型来说，一个最大的不同在于假设具有机动的目标加速度不能任意变化，机动目标下一时刻的加速度只能在机动目标当前时刻的加速度附近进行变化，因此基于“当前”统计模型的机动目标跟踪得到了广泛的研究[1-3]，并且对机动目标的跟踪性能相对较好[4-5]。

在多目标跟踪中，基于“当前”统计模型的自适应卡尔曼滤波的联合概率数据关联算法对杂波环境下的多机动目标跟踪具有良好的性能。但由于基于“当前”统计模型的自适应卡尔曼滤波需根据经验值对机动频率和加速度方差进行预先设定，根据经验值预先设定往往难以满足复杂环境下的多机动目标跟踪，预先设定的经验值可能造成状态过程噪声过大或过小，在利用联合概率数据关联算法对多目标进行关联跟踪时，这样的状态过程噪声将直接影响目标的量测预测值，影响落入跟踪门内的量测数目。在杂波数的增加、目标相互交叉以及目标发生机动等情况下，目标误跟及跟踪丢失现象就会发生，严重情况下，将会导致大量目标跟踪丢失，通过控制跟踪门可以有效减少杂波数进入跟踪门内的数量，也可以有效减少相互交叉的公共区域，从而减小计算量以及杂波之间的相互干扰。因此好的跟踪门可以大大提高Java平台调适架构（Java Platform Debugger Architecture，JPDA）算法的跟踪性能，为解决基于“当前”统计模型的自适应卡尔曼滤波的联合概率数据关联算法在跟踪多机动目标时出现的这种问题，本文在已有算法的工作基础上，采用数学推导的方式导出了机动频率的近似数学表达式，一定程度上避免了对不合理经验值设定的依赖。最后通过仿真实验，对所提算法进行了仿真验证。

1 基于“当前”统计模型的单目标自适应卡尔曼滤波算法

将“当前”统计模型和卡尔曼滤波算法相结合，就得到了自适应卡尔曼滤波算法。

离散时间情况下目标状态方程表达如下

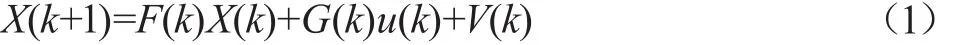
式（1）中，X(k)为目标k时刻的状态向量，F(k)为状态转移矩阵，G(k)是控制输入矩阵；u(k)为已知输入。V(k)是高斯白噪声，均值为零、协方差为Q(k)，且不同时刻的过程噪声是相互独立的，过程噪声表达式如下。

与目标状态方程对应的量测方程为：

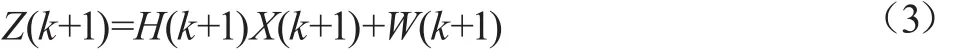
式中，H(k+1)为目标对应的量测矩阵，W(k+1)为高斯白噪声序列，其均值为零、协方差为R(k+1)，不同时刻的观测噪声也假定是相互独立的，则对应表达式为：

从式（1）及式（3）可得标准卡尔曼滤波算法如下：

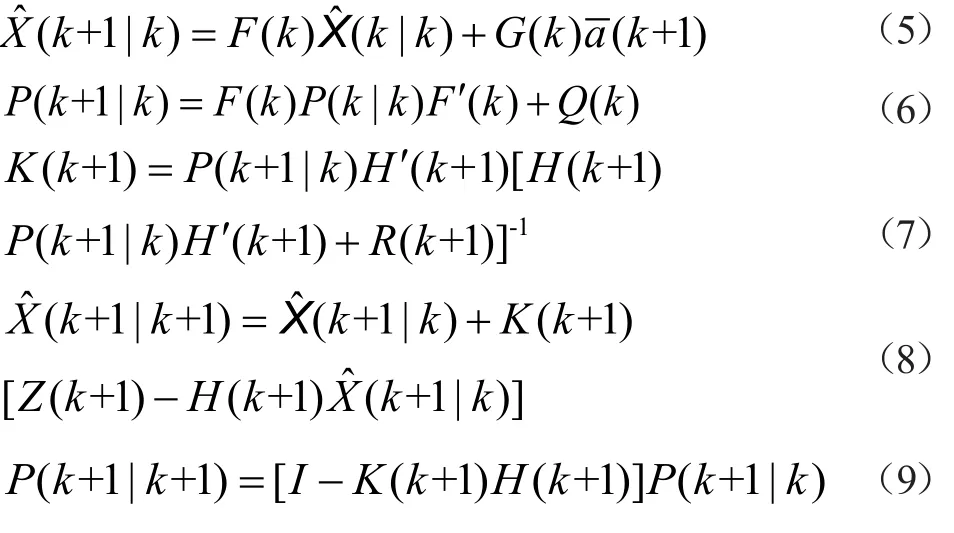
“当前”统计模型将˙˙(k+1)的一步预测值˙(k+1 |k)看作是(k+1)T时刻瞬时机动加速度均值，即：

在采样周期较小时，将k时刻的加速度值看作是k+1时刻加速度一步预测值，即：

结合“当前”统计模型和上述假设可得如下表达式：

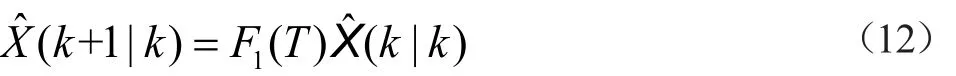
其中：

加速度方差为：

基于“当前”统计模型的自适应卡尔曼滤波算法主要步骤如下：

α为目标机动频率，根据目标机动情况而设定的常数，通常根据经验值进行设定。实际情况下，机动目标不可能一直处于某种机动状态进行运动，此时如果预先根据经验值对机动频率进行设置，就不能实时反应目标的机动状态，机动频率设置的不合理，通过式（15）至式（20）可以直观看出，将直接影响机动目标的过程噪声、影响机动目标的状态协方差，从而影响机动目标的状态，造成机动目标跟踪精度的下降。为加速度方差，式（14）加速度方差表达式中也需要根据经验值设定机动目标机动的最大加速度，因此同样会导致和机动频率设置不合理一样的问题。

2 基于“当前”统计模型的单目标自适应卡尔曼滤波算法改进

通过基于“当前”统计模型自适应卡尔曼滤波算法的分析可知，在经典的“当前”统计模型中，机动频率和加速度极大值需根据经验设定，这类方法在处理多目标跟踪时往往由于依据经验值设置不合理使得每一步滤波算法得到的目标状态、预测值的协方差与实际严重不符合，在利用基于“当前”统计模型的自适应卡尔曼滤波算法对多目标进行关联跟踪时，将会影响数据关联门的合理设置，而数据关联门的设置不合理，又会对杂波环境下多目标跟踪数据关联算法实现带来影响，增加算法的计算量，降低算法跟踪精度。因此机动频率及加速度极大值的设定已经成为自适应卡尔曼滤波算法研究的瓶颈，针对此问题许多学者提出了改进的算法[4-6]，但多数都只是针对加速度方差进行改进[7-8]，对机动频率自适应改进较少。针对机动频率根据经验值设定不合理现象，本节提出了相应的改进措施，一定程度上实现了机动频率自适应。

2.1 机动频率自适应

从2节的分析可知在基于“当前”统计模型的自适应卡尔曼滤波算法中，通常假定机动频率α为常数，而实际在目标机动过程中机动频率应该是随着时间的变化而时刻变化的，因此设为常数是不合理的。

a(t)为加速度am(t)的加速度噪声，在“当前”统计模型中，在一个采样周期内，其瞬间的加速度均值为一个常数，实际情况下，加速度均值是时刻在变化的。

通过文献[9]可知，经典“当前”统计模型加速度、加速度噪声及加速度均值之间有如下表达式：对式（22）两边进行求导，得到如下表达式：

将式 （23）代入式（21），得到如下表达式：

假设式（24）中w(t)是均值为0，方差为的白噪声，并服从高斯分布，在这种假设下，可以得到如下表达式：

式（25）中x服从正态分布，即x～N(0,1)，将式（25）代入式（24）并整理可得如下表达式：

对式（26）进一步整理可得：

对式（27）可以分两种情况进行讨论：

对式（28）进行离散化处理得：

对式（29）两边进行求期望，即：

因为x服从N(0,1)正态分布，故E(x2)=1，因此上式可以近似表示为：

由式（31）可以进一步得出k时刻机动频率近似表达式如下：

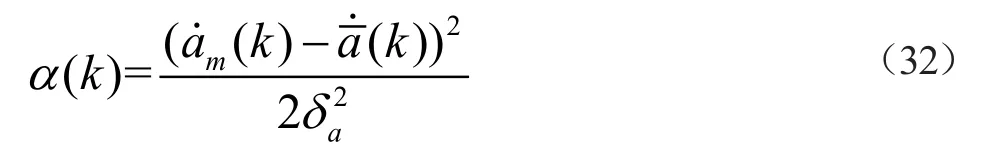
(k)表示k时刻机动加速度均值变化率，文献[9]指出(k)可以用k时刻的状态的一步预测值来表示，在采样周期较小时也可以用目标在k－1时刻的状态值来表示。因此可以利用前两个时刻的加速度变化来近似表示k时刻机动加速度均值变化率，表达式如下：

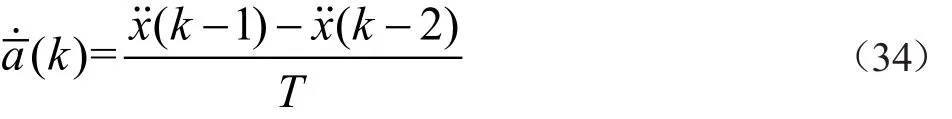
将式（33）、（34）代入式（32）可得

（2）如果am(t)−(t) ≠ 0，即目标当前时刻的速度和目标在此时刻的瞬间加速度均值不相等，表明此时目标正在进行变加速运动。在该情况下式（27）可以看作关于机动频率α的一元二次方程，利用求根公式可以得出机动频率的表达式如下：

对式（36）离散化得：

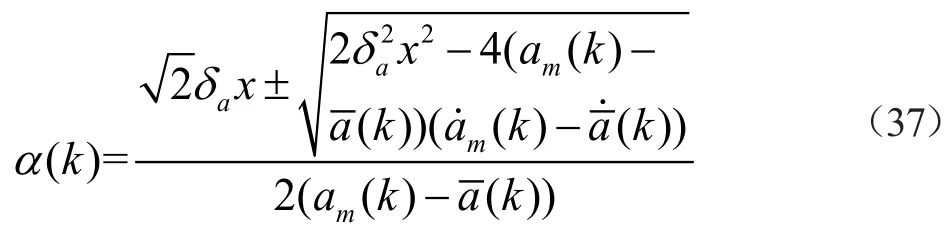
对式（37）两边同时求期望得：

式（38）中E(x)=0，E(x2)=1，故对式（38）进行整理可得：

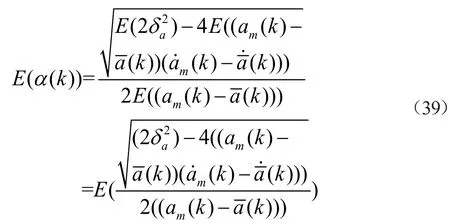
机动频率都为正数，由式（39）可以进一步得到k时刻机动频率α的近似表达式如下：

式中为加速度方差，将式（3-33）、（3-34）代入式（40）整理得：

通过式（35）及式（41）可得机动频率自适应的近似表达式为：

2.2 加速度方差自适应

根据文献[10]可知，利用目标状态估计值与状态预测估计值之间的差值可以得到了一种新的加速度方差自适应表达式。

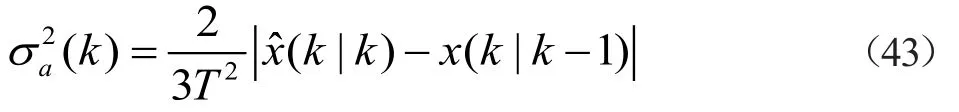
加速度方差σ2α(k)的物理含义为：目标加速度的方差应该和加速度的变化率相关，在一个采样周期内，加速度变化率越大，对应的加速度方差就越大，反之加速度方差就越小。从式（43）可以看出当目标处于非机动或者弱机动时，目标k时刻的状态值与状态一步预测值相差较小，此时加速度方差较小，当目标处于强机动时，k时刻状态估计值与k时刻状态一步预测值相差很大，此时加速度方差较大，符合加速度方差)的物理含义。本文参考文献[10]结论，一定程度上解决了预先设定加速度极限值带来的跟踪误差。

3 基于联合概率数据关联的多目标自适应跟踪算法（IAFJPDA）

通过分析可知，在利用联合概率数据关联算法进行机动目标数据关联跟踪时，第一步应该首先确定跟踪门，跟踪门是以目标量测预测位置为中心，向外延伸的一块区域，这块区域表示目标下一时刻观测量测值可能出现的位置。跟踪门设置的目的在于尽可能将与目标相关的量测放入门内，将来自其他目标的量测和杂波干扰拒之门外。从椭圆（球）跟踪门以及滤波算法可以看出，机动目标状态过程噪声Q(k)影响目标状态一步预测协方差，从而影响目标状态更新，随着时间的不断迭代，进一步不断影响目标量测值，影响到椭圆门限的取值大小，最终影响落入目标N的跟踪门内量测数的数量，如果Q(k)取值过大，可能导致更多与目标关联的量测值被拒之门外，如果取值过小，可能导致更多与目标不相关的量测值落入跟踪门内，这样将增加算法的计算量，严重情况下将会出现组合爆炸现象，大大降低算法的跟踪性能，因此Q(k)如果仅仅根据经验值进行设定，在复杂的运动场景下将很难设置合理的状态过程噪声来调整落入跟踪门内的量测值的数量。自适应卡尔曼滤波算法的出现较好解决了这一问题，但是存在机动频率和加速度方差不能自适应一定程度上也会出现上述问题。为解决此问题，本文首先对机动频率和加速度方差进行调整，提出了改进的自适应卡尔曼滤波算法，然后将改进的自适应卡尔曼滤波算法和联合概率数据关联算法相结合，得到了基于联合概率数据关联的多目标自适应跟踪算法。该算法一定程度上解决了原自适应卡尔曼滤波跟踪算法中存在的问题。该算法具体步骤如下：

第一步，给定目标初始状态

第二步，状态的一步预测

第三步，量测的一步预测

第四步，预测协方差

第五步，新息

第六步，新息协方差

第七步，椭圆跟踪门门限

第八步，生成确认矩阵Ω

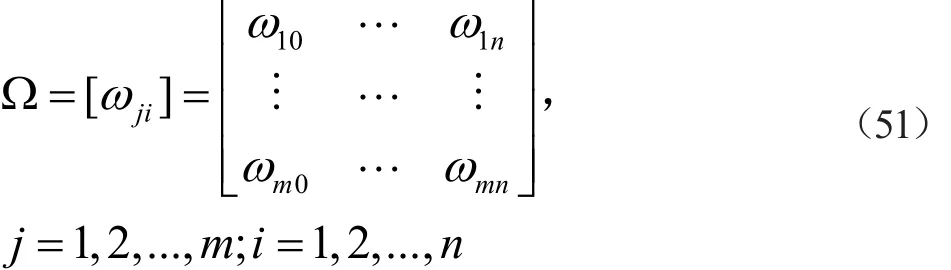
第九步，得到全部联合事件θt(k)

第十一步，根据联合事件概率计算关联概率βji(k+1)

第十二步，卡尔曼滤波状态更新

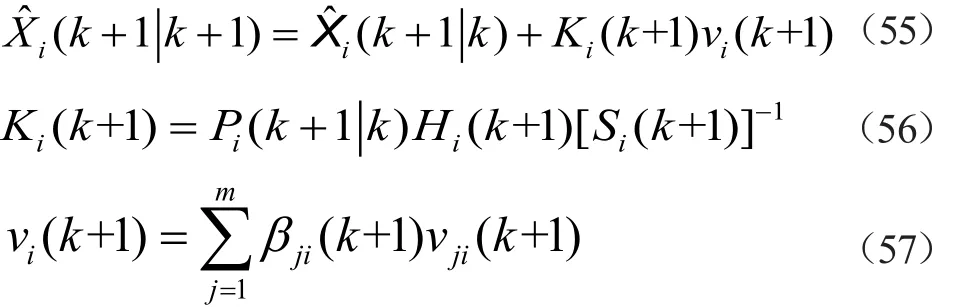
第十三步，状态估计协方差更新

4 仿真实验

本节目的在于通过仿真实验验证3节所提改进的自适应联合概率数据关联算法的有效性。仿真在目标进行非机动（匀速）及圆周机动场景下进行。

目标1的初始位置为x0=16 000 m，y0=10 000 m，z0=1 000 m，目标2的初始位置为x0=15 000 m，y0=9 000 m，z0=1 000 m，目标刚开始作匀速直线运动，目标1初始速度为v=-310 m/s，目标2初始速度为v=-320 m/s,目标1和目标2初始时刻以加速度为10 m/s2做匀加速运动，初始匀速运动时间为[0，5]s，而后目标在平面内作一周圆周机动，目标1圆周机动时间为89 s，目标2圆周机动时间为86 s，最后目标继续作匀速直线运动，目标1匀速运动时间为21 s，目标2匀速运动时间为24 s，仿真中量测噪声建模：假设量测噪声与距离存在关系式V(k)=(βx(k)+Δx0)ω(k)，其中ω(k)是均值为0，方差为1的正态伪随机数，Δx0=100 m，则R(k)=(βx(k)+Δx0)2E[ω2(k)]为噪声方差。

算法性能评价指标为均方根误差：

式（67）中N为蒙特卡洛仿真次数，实验中N=20，i为第i次蒙特卡洛仿真，x(k)，分别为k时刻目标状态的真实值和估计值。仿真对比了基于自适应卡尔曼滤波结合JPDA的AF-JPDA算法及本文提出的基于联合概率数据关联的多目标自适应跟踪算法（IAF-JPDA）。在机动频率和加速度极大值取不同值情况下进行了两组对比仿真实验，目的在于验证本文所提基于联合概率数据关联的多目标自适应跟踪算法的有效性。

实验一：杂波密度：λ=0.000 04，门限g=16，检测概率PD=0.99。最大加速度αmax=20，α=0.01，Q=100，仿真结果如图1—2所示。

将式（51）代入式（62）得：

第十四步，过程噪声的实时更新

式中字母的具体含义参考2节，基于“当前”统计模型。第十五步，循环，k=k+1时，跳转到第二步。

图1 目标跟踪轨迹

图2 位移均方根误差

实验二：杂波密度：λ=0.000 04，门限g=16，检测概率PD=0.99。最大加速度αmax=50，α=0.3，Q=100，仿真结果如图3—4所示。

两组实验主要是在不同机动频率和加速度极大值情况下进行的仿真实验。机动频率越大，表示目标机动越大，此时可以设置较大加速度，反之机动频率设置较小，对应最大加速度也应该设置较小，本章根据经验设定两组实验参数，实验一最大加速度αmax=20，机动频率α=0.01，实验二最大加速度αmax=50，机动频率α=0.3。可以看出，目标1在圆周机动时间[6，94]s和目标2在圆周机动时间[6，91]s内，基于自适应卡尔曼滤波的JPDA算法（AF-JPDA）及本文所提基于联合概率数据关联的多目标自适应跟踪算法（IAFJPDA），在对多目标进行跟踪时，跟踪性能相差不大，本文所提算法（IAF-JPDA）性能只是稍好于自适应卡尔曼滤波的JPDA算法（AF-JPDA）。目标1、目标2处于弱机动（[0，5]）s和匀速运动时，跟踪性能相对较差。从目标1匀速运动时间（[95，116]）s和目标2匀速运动时间（[92，116]）s，实验一中目标1和目标2在x方向的位移均方根误差（见图2）和实验二中目标1和目标2在x方向的位移均方根误差（见图4），通过对比可以发现，随着机动频率和加速度极大值设置较大，处于匀速运动的目标1和目标2跟踪性能急剧下降，跟踪误差较大，而本文所提基于联合概率数据关联的多目标自适应跟踪算法（IAF-JPDA），在对目标进行跟踪时，保持了较好的跟踪性能，目标跟踪性能并未出现较大跟踪误差。

5 结语

本文首先介绍了基于“当前”统计模型的自适应卡尔曼滤波算法，并针对基于“当前”统计模型自适应卡尔曼滤波算法中需根据经验值设定机动频率和加速度极大值不合理现象进行了改进，提出了一种新的机动频率自适应表达式，重新设计了自适应卡尔曼滤波算法。提出了改进的基于“当前”统计模型的自适应卡尔曼滤波算法，将改进算法结合JPDA算法，形成了对多机动目标跟踪的IAF-JPDA算法。通过两组仿真实验，从实验结果可以看出，本文所提算法一定程度上解决了基于“当前”统计模型自适应卡尔曼滤波算法在进行机动目标跟踪时，参数预先设置不合理导致的机动目标跟踪误差问题，有效提高了机动目标跟踪精度，表明本文所提算法的有效性。

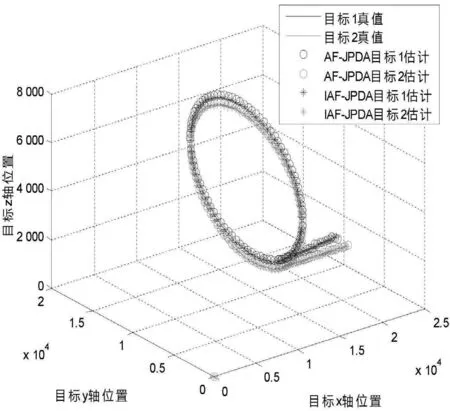
图3 目标跟踪轨迹

图4 位移均方根误差