水下航行器航行任务可靠度综合评定法

罗晓强, 王 浩, 侯发林



水下航行器航行任务可靠度综合评定法

罗晓强1, 王 浩2, 侯发林1

(1. 中国人民解放军91388部队, 广东 湛江, 524022; 2. 中国人民解放军92819部队, 辽宁 大连, 116041)

水下航行器航行任务可靠度的传统考核方法是将非全航程的条次当作全航程条次统计, 不符合指标剖面要求。针对传统考核方法存在的不足, 提出将航行过程看成是寿命服从指数分布型的综合评定方法, 该方法统计各条次的实航时间, 结合其他分系统的试验数据, 利用L-M法综合折算总的试验任务条次数及失效数, 以基于二项分布的置信下限法计算任务可靠度最低可接受值, 并以此判断任务可靠度是否满足指标要求。研究表明, 该方法解决了传统考核方法的不足, 实施容易、操作简单、结论可靠, 提高了试验效率。

水下航行器; 任务可靠度; L-M法; 二项分布; 置信下限; 实航试验

0 引言

考核水下航行器的航行任务可靠度时, 由于全系统试验的样本量比较少, 往往采用金字塔式系统可靠性综合评定方法进行评定, 即将分系统试验数据折合成全系统试验数据后再进行评定。在以往水下航行器航行任务可靠度鉴定试验中, 常采用的方法是将各分系统单元的试验结果看作服从成败型, 这样可直接采用经典L-M(Levenberg- Marquardt)法[1-2]进行系统可靠性综合评定, 此方法计算简便, 但是存在将非全航程的众多条次试验当作一次全航程统计, 不符合指标要求, 不能真实反映航行任务可靠性水平。

针对类似情况, 文献[3]和[4]提出了将航行过程当作指数型考核鱼雷实航工作可靠度的方法, 而水雷等其他水下航行器, 目前未见相关文献。

参考文献[3], 文中提出了基于航行时间累计的成败型分系统和指数型分系统串联的L-M可靠性综合评定方法, 用于评定水下航行器任务可靠性, 主要适用于自航水雷及剖面相似的其他航行器。

1 航行任务剖面

水下航行器航行任务剖面一般包括: 航行器布放准备, 航行, 至航行结束后完成相应要求的功能, 以及所经历的全部事件和环境的时序描述。主要事件包括: 布放(含布放准备)、航行、动作等。因此, 水下航行器进行航行试验时, 既可以看作是全系统的试验, 也可以看作是布放(含布放前准备)、航行、结束航行时的动作分别由3个相应的分系统串联完成的3个试验[5]。当航程为全航程、试验剖面内功能动作完整时, 可看作是全系统的1次试验, 否则只统计相应的分系统试验数。

2 试验数据类型分析

一般情况下, 在任务可靠性指标鉴定试验工程应用中, 为了方便计算, 主要采用基于成败型进行评定, 如鱼雷实航工作可靠度[6]等。部分采用指数型[7-8], 如平均故障间隔时间(mean time between failure, MTBF)等。根据文献[9], 凡在一段时间内不积累损伤, 也不积累疲劳, 仅由于外界超强度冲击力的随机到来或内部潜伏的隐患偶然爆发所造成的故障, 都是随机的偶然故障, 基本服从指数分布, 电子产品和复杂机械产品的寿命绝大多数是服从指数分布的, 且经过长时间调试后的整机或系统的寿命基本上服从指数分布。因此, 在研究水下航行器可靠性问题时, 也完全可以按指数分布来分析处理。

综上, 根据水下航行器航行试验的特点, 航行任务可靠度试验数据类型可按如下处理:

1) 全航程的实航试验, 按成败型数据统计, 即记1次全系统的试验数;

2) 布放试验(含布放前准备), 按成败型数据统计, 即记1次布放试验数;

3) 结束航行时的动作试验, 按成败型数据统计, 即记1次结束航行时的动作试验数;

4) 航行试验, 按指数型数据统计, 统计航行时间, 以及期间发生的责任故障数。

3 综合评定方法

3.1 评定思路

综合可靠度评定方法是基于实际试验数据, 利用其他分系统的试验数据和收集到的相关产品数据等, 进行金字塔式评定可靠度的方法, 将下一级单元系统向上一级单元系统折合, 并采用单侧置信下限法进行评定。此方法用较少的全系统试验数据和大量的分系统试验数据, 即可完成任务可靠度评定。水下航行器任务可靠度综合评定方法评定思路及步骤如下。

1) 统计全系统实航试验数据

整理、分析全系统的实航试验数据, 并将数据折合为同一环境条件下的数据, 如实验室实验数据、实航试验数据以及其他不同阶段的不同地点试验数据等。折合时, 环境因子由试验方和研制方按照相关确定方法共同确定。统计时, 数据类型为成败型, 并记试验数为, 试验失败数为。

2) 折合分系统等效试验数据

第1步: 将布放试验数据、航行试验数据和航行结束后的动作试验数据, 按照环境因子分别折合成同一环境条件下的数据。

第2步: 按照L-M法, 对成败型的布放试验数据(1,1)、航行结束后动作试验数据(2,2)进行综合, 得到等效试验数(4,4)。

第3步: 将指数型的航行试验数据, 根据任务时间折合得到航行等效试验数据(3,3), 并转换为成败型等效试验数据(5,5)。其中, 所有航行试验的航行时间均纳入统计。

3) 综合评定

根据L-M法, 利用(4,4)、(5,5)和(,), 综合得到航行全系统总试验数据(,), 并通过查询文献[10]或计算, 得到航行任务可靠度的下限值。

评定思路见图1所示。需要注意的是, 在使用数据前即进行数据折合前, 要根据相关分布检验方法进行数据分布类型的检验。实际工程应用中, 因缺少足够的样本数和故障数等信息, 可能检验的结果不够准确, 此时要进行工程分析, 如产品技术状态是否一致、试验条件差异性等, 确保数据类型是一致的。

3.2 成败型数据折合方法

用L-M法对成败型的布放试验数据(1,1)、航行结束后动作试验数据(2,2)进行综合, 得到成败型等效试验数(4,4)。方法如下

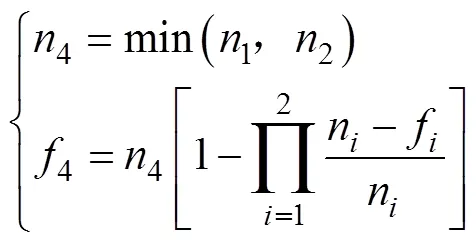
3.3 数据分布类型转换方法

数据分布类型的转换, 采用文献[1]提供的方法将指数型航行等效试验数转换为成败型数据。

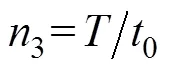
当3≠0时, 有

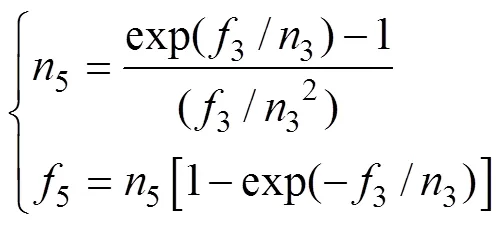
当3=0时, 有

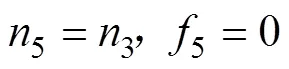
3.4 任务可靠度综合评定方法

在众多评定方法中, L-M方法相对较保守, 因此主要采用文献[1]提供的L-M方法任务可靠度综合评定。记全系统总等效试验数为(,), 则由全系统的实航试验数(,), 以及(4,4)和 (5,5), 可计算出系统综合试验数。计算方法如下

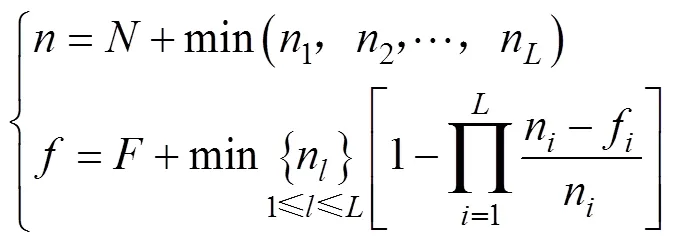
式中,≠。当=时,R为0。

上述用式(5)求解时, 文献[10]还有更详细的求解过程。在实际应用过程中, 可根据试验数、失败数与置信度, 查询文献[10], 得到置信下限值。当和不是整数时, 用线性插值进行计算。

4 方法应用要求

水下航行器使用上述方法进行航行任务可靠度试验与评定时, 应满足以下几个要求: 1) 规定全系统试验最少数; 2) 规定全系统试验数允许失败数; 3) 使用分系统试验数据时, 要保证被试航行器的技术状态一致, 或者改进的技术状态不影响试验结果, 保证数据类型一致; 4) 故障统计与处理, 要严格按照相关国军标进行; 5) 使用不同环境与条件下获得的数据时, 根据相关要求, 明确环境因子。

5 实例分析

假设某水下航行器航行任务可靠度指标要求为任务时间2 h, 可靠度0.8(=0.8)。根据指标要求, 至少需要航行时间超过2 h的8次试验且无故障, 指标才能判定合格。

一般情况下, 为了考核某些无法在全航程中结合考核的功能性能指标, 往往会有一些短航程或非全航程的试验条次, 如适应高海况试验等。假设该水下航行器在海上试验中, 在同样的使用条件和要求下分别进行了18次试验, 均成功或在第1次试验航行阶段发生故障, 见表1。每次试验动作流程都是完整的, 即都包含了布放、航行、航行结束时动作等。

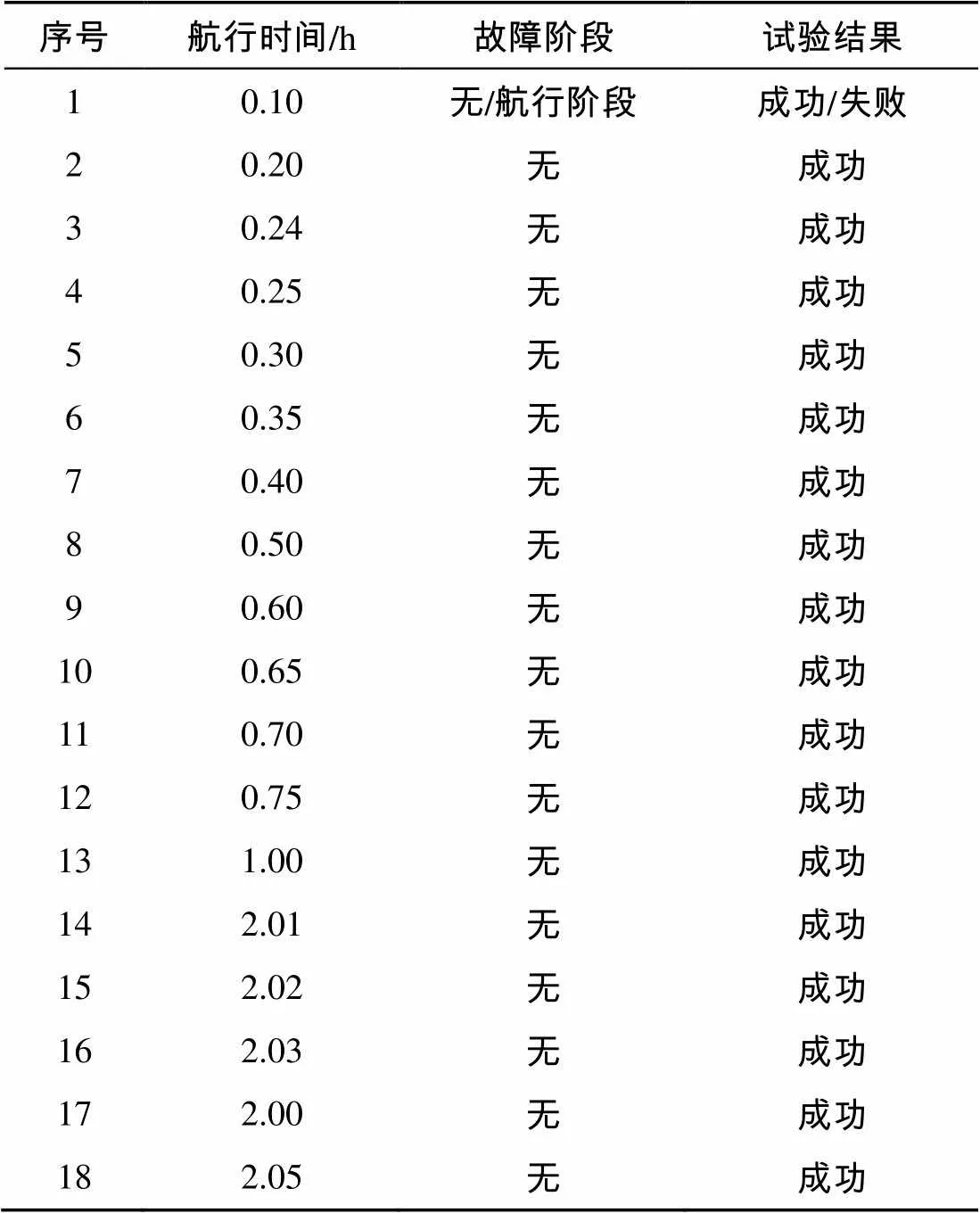
表1 试验数据表

表1中, 全航程的试验只有5次, 若直接用成败型算法, 要么再进行3次航行时间超过2h的试验或者将短航程的试验当作全航程的试验, 不然样本量不足以评定任务可靠度。若根据文中的算法, 上述18次试验结果已可以做出判断。计算结果如下。

1) 当所有试验均成功时

表1中, 全系统试验数=5, 失败数=0; 布放试验数(1,1)=(13, 0); 航行结束时动作试验数(2,2)=(13, 0); 航行试验航行累计时间6.04 h, 失败0次, 即等效试验数(3,3)=(3, 0)。

根据式(1), 将(1,1)、(2,2)进行综合, 得到等效试验数(4,4)=(13, 0);

根据式(3), 将指数型数据(3,3)转换为成败型数据(5,5)=(3, 0);

根据式(4), 将(,)、(4,4)和(5,5)进行综合, 得到总试验数=8, 失败数=0。经查询文献[10], 得到任务可靠度置信下限值0.82 (=0.8), 此时任务可靠度满足指标要求。

2) 当在航行阶段出现一次失败时

在13次非全航程的航行试验中, 出现1次失败, 那么根据式(2), 航行试验等效试验数(5,5)=(3.6, 1.0); (4,4)仍为(13, 0)。由式(4), 得到总试验数8.6, 失败数1.0。根据线性插值计算, 得到任务可靠度置信下限0.69(=0.8), 此时任务可靠度不满足指标要求。

其他试验数和故障数的情况, 计算方法类似。

评估结果及准确性分析如下: 1) 试验是在相同的试验条件、试验环境(海上实航试验)、技术状态下进行的, 不同条次的试验数据类型一致, 不用进行环境因子转换; 2) 不管短航程还是长航程, 航行时间、故障数均纳入了试验的统计, 数据覆盖全面、真实和有效; 3) 采用较保守的L-M算法, 控制了考核风险; 4) 该方法既不用增加全系统的试验次数, 也避免了短航程无法纳入全系统试验次数统计的问题。

6 结束语

通过开展对水下航行器航行任务可靠度综合评定法的相关研究, 结果表明: 该方法计算简单、结果可靠、可操性强, 解决了传统考核方法将非全航程当作全航程条次纳入统计的不足, 并减小了对全系统试验数据的依赖程度, 提高了试验效率。

[1] 中国人民解放军第二炮兵第四研究所. GJB3105-1997 战略导弹武器系统性能评定方法[S]. 北京: 国防科学技术工业委员会, 1997.

[2] 驻航天总公司七七一所军事代表室. HJB54-1993 武器系统及设备可靠性评定要求和方法[S]. 北京: 中国人民解放军海军装备技术部, 1993.

[3] 贺成刚, 叶豪杰, 张迪. 一种改进的鱼雷实航工作可靠度评定方法[J]. 鱼雷技术, 2011, 19(6): 411-414.He Cheng-gang, Ye Hao-jie, Zhang Di. An Improved Method for Evaluating Torpedo’s Working Reliability in Sea Trial[J]. Torpedo Technology, 2011, 19(6): 411-414.

[4] 朱文振, 王松林, 王昊. 一种电动力鱼雷实航工作可靠度评估方法[J]. 水下无人系统学报, 2017, 25(3): 293-296.Zhu Wen-zhen, Wang Song-lin, Wang Hao. A Working Reliability Assessment Method for Electric Power Torpedo in Sea Trial[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 293-296.

[5] 中国人民解放军总参谋部工程兵工程装备论证试验所. GJB3675-1999 陆军沉底、上浮水雷设计定型试验规程[S].北京: 中国人民解放军总装备部, 1999.

[6] 武器装备综合论证研究所. GJBz20391-1997鱼雷可靠性鉴定与验收试验方法[S]. 北京: 中国人民解放军总参谋部, 1997.

[7] 武小悦. 装备试验与评价[M]. 北京: 国防工业出版社, 2008.

[8] 中国人民解放军总装备部电子信息基础部标准化研究中心. GJB899A-2009 可靠性鉴定与验收试验[S]. 北京: 中国人民解放军总装备部, 2009.

[9] 孟庆玉. 舰艇武器装备可靠性工程基础[M]. 武汉: 海军工程大学, 2006.

[10] 东北师范大学, 北京师范大学, 中国标准化研究院. GB/T4087-2009 数据的统计处理和解释二项分布可靠度单侧置信下限[S]. 北京: 中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会, 2009.

(责任编辑: 许 妍)

Comprehensive Assessment Method for Navigation Mission Reliability of Undersea Vehicle

LUO Xiao-qiang1, WANG Hao2, HOU Fa-lin1

(1. 91388thUnit, The People’s Liberation Army of China, Zhanjiang 524022, China; 2. 92819thUnit, The People’s Liberation Army of China, Dalian 116041, China)

Conventional reliability assessment method of undersea vehicle navigation mission regards incomplete course statistics as whole course statistics, which does not meet the requirements of the specification profile. In view of the shortcomings of conventional assessment methods, a comprehensive assessment method is proposed, which the navigation process is considered to be an exponential distribution of life, and the time of actual navigation is counted and converted into a mission equivalent number according to the time of the whole course. Combining with other subsystems’ trial data, the L-M method is used to calculate the number of times and the number of failures of the total sea trial task. The smallest acceptable value of mission reliability is calculated with the lower confidence limit method based on the binomial distribution for determining whether the reliability of the task meets the requirement. It is concluded that the proposed method solves the shortcomings of theconventional assessment method, and is easy in implement, simple in operation, and reliable in assessment, and this method can greatly reduce the number of trial times and improve the efficiency of trial.

undersea vehicle; mission reliability; L-M method; binomial distribution; lower confidence limit; sea trial

A

2096-3920(2018)04-0348-04

10.11993/j.issn.2096-3920.2018.04.012

TJ630.6; TB114.37

罗晓强, 王浩, 侯发林. 水下航行器航行任务可靠度综合评定法[J]. 水下无人系统学报, 2018, 26(4): 348-351.

2017-12-12;

2018-04-08.

罗晓强(1985-), 男, 硕士, 工程师, 主要研究方向为水中兵器试验技术.