基于单信标纯方位测量的AUV水下定位方法

李佳橦, 张 臣, 张宏欣



基于单信标纯方位测量的AUV水下定位方法

李佳橦, 张 臣, 张宏欣

(中国人民解放军 91439部队, 辽宁 大连, 116041)

在信标深度已知条件下, 提出了一种基于单信标纯方位信息测量的自主水下航行器(AUV)实时定位方法, 以解决单信标AUV水下定位中遇到的问题。不同于传统基于单信标测距信息方法, 文中从坐标变换原理出发, 构建了2自由度(2-DOF)姿态的AUV运动模型, 推导了深度已知条件下纯方位AUV定位的状态空间模型, 在所建立模型的基础上采用扩展卡尔曼滤波器(EKF)进行求解, 并针对EKF算法应用给出了一种滤波器调参方法, 通过构建仿真试验对所提出方法进行了有效性验证, 并将其与现有方法进行了对比分析。结果表明, 在该仿真条件下, 文中基于单信标方位观测模型的方法在滤波精度上要好于基于测距信息的方法, 且收敛性能优于后者。

自主水下航行器; 定位方法; 单信标; 纯方位测量; 扩展卡尔曼滤波器

0 引言

自主水下航行器(autonomous undersea vehicle, AUV)已经在军民领域得到了广泛应用, 正向着高度自主化、长航时化方向发展。精确自主定位是提高AUV自主能力的关键要素。受应用成本的限制, 一般AUV难以搭载高精度的惯性导航系统(inertia navigation system, INS)。因此其自身航位推算能力较差, 误差增长过快, 一般需采用外部辅助传感器获得载体坐标系相对于参考坐标系的信息。由于GPS信息在水下不可用, 使得声学定位方法成为事实上的水下导航辅助手段。

由于单声信标能够有效降低系统部署和回收成本, 近年来, 基于单信标的水下定位方法得到广泛的关注[1-3]。曹俊等[4-5]在AUV为直航的假设下, 基于单信标测距信息, 采用离线迭代方法求解其初始位置进行推算。张福斌等[6]基于单信标测距信息, 利用Kalman滤波器将其与惯导/多普勒计程仪信息进行融合, 提高了AUV的导航精度。曹方方等[7]及Vallicrosa等[8]分别基于单信标测距信息, 在AUV自身偏航角度已知条件下, 利用滤波算法对AUV进行实时定位。严卫生等[9]进一步就单信标测距AUV定位可观测性进行了分析, 指出测距定位需要方位信息辅助才可满足系统可观测性条件。曹俊等[10]对单信标测距误差及其影响进行了分析, 指出了测距误差主要源于收发异步问题。

根据已公开的文献资料可知, 单信标AUV水下定位研究多是基于距离观测信息进行的, 这一方面是由于近场水声测距技术精度普遍比较高[4], 另一方面是由于基于距离的观测模型复杂程度及非线性度均低于角度观测模型, 实际算法设计时的调参较为容易。但对于测角信息利用方面则研究较少, 而测角相对测距具有成本低、易实现和方便实施的优势。Matsebe等[11]借助即时定位构图技术框架(simultaneous localization and mapp- ing, SLAM), 研究了基于角度-距离信息的AUV- 信标同步定位方法[12]。Becker等[13]受测角SLAM技术启发, 提出了基于方位信息的AUV-信标同步定位方法, 但假设AUV载体是水平运动的。在上述研究基础上, 文中提出一种在信标深度已知条件下, 基于信标纯方位信息的AUV定位方法, 构建了考虑2自由度(degree of freedom, DOF)姿态的AUV定位模型, 采用扩展卡尔曼滤波器(ex- tended Kalman filter, EKF)进行求解, 并针对估值滤波器的选择及调参方法进行了分析, 并通过仿真分析对所提出方法进行了验证。

1 模型构建

由于文中仅针对单信标定位问题, 为简化问题表述, 不考虑AUV当地导航平面相对于地心地固坐标系的转动, 故参考坐标系可选为当地东(east)-北(north)-天(up)导航坐标系(下文称系), 其中东向为轴, 北向为轴, 天向为轴, 且坐标原点位于海底。AUV与信标的定位计算结果均为ENU坐标。对于进一步的自主导航误差修正应用, ENU坐标可方便的向其他参考系进行转换[14]。

通过式(1)可得系中的信标方位单位矢量

对于AUV运动建模, 考虑其低动态刚体特性, 可假设加速度方向始终沿系轴(前向), 且与速度方向一致, 无横倾及平移运动, 则其离散时间运动模型

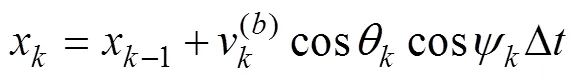
利用式(3)可将以上写为矩阵形式

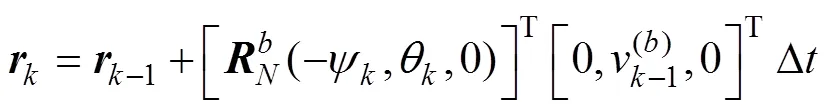
1.1 状态模型

在上述基础上, 综合其他变量得到状态向量

其中, 状态转移矩阵为

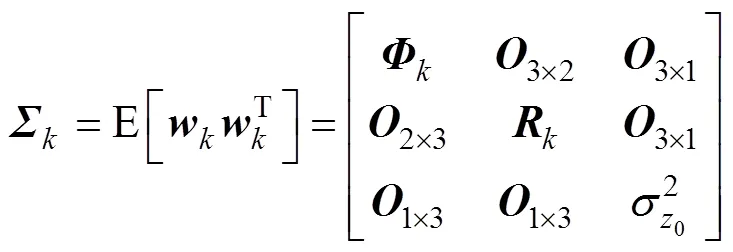
1.2 观测模型

观测信息为信标相对于AUV的俯仰角和方位角,时刻AUV测得的角度

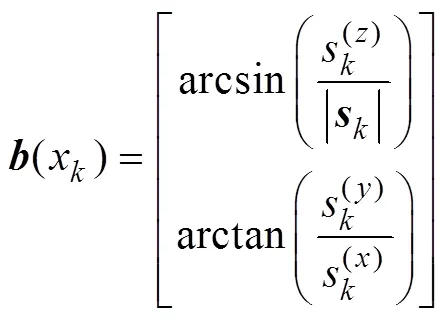
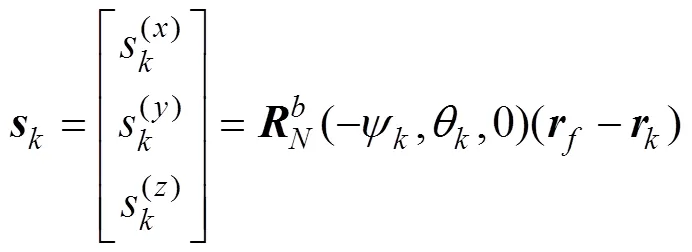
根据式(2)~(5), 可得

根据上述建模过程可知, 状态空间模型(12)和(18)分别为线性状态方程和非线性观测方程, 而根据式(6)~(10)可知, 其可观测性等价于如下的非线性状态方程和线性观测方程

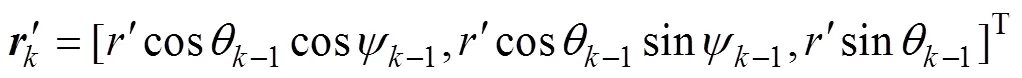
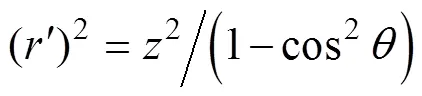
式(21)~(23)表明, 在给定观测信息, 即深度和空间方位(俯仰角和偏航角)条件下, 可以唯一的确定AUV的位置, 因此上述建立的状态空间模型是可观测的。

1.3 滤波求解

可见上式是一个线性模型, 可直接利用卡尔曼滤波进行求解, 其中线型新的观测值

状态预测

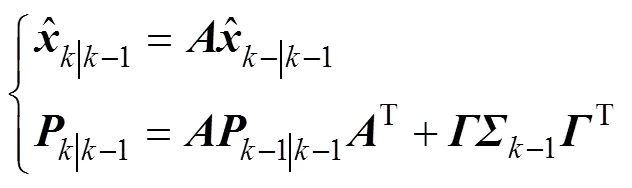
观测更新

虽然已有无迹卡尔曼滤波(unscented Kalman filter, UKF)、容积卡尔曼滤波(cubature Kalman filter, CKF)及粒子滤波(particle filter, PF)等其他典型估值滤波器可选, 但考虑到如下情况:

1) 文中模型的非线性仅反映在观测模型上, 且AUV运动特性决定了其过程噪声并不大, 在这种条件下, UKF与CKF相对于EKF在处理大过程噪声及非线性模型时的优越性不明显;

2) EKF作为一种应用已久的算法[16], 已经有大量实际工程化算法[17-19], 更适合作为衡量文中建立算法模型性能的参考方法;

3) EKF是目前非线性滤波中相对复杂度最低的一种方法, 更适合实时应用[19]。

因此文中仍采用传统的EKF进行求解, 关于进一步的算法对比分析将在仿真中结合算例具体给出。

2 仿真结果与分析

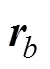
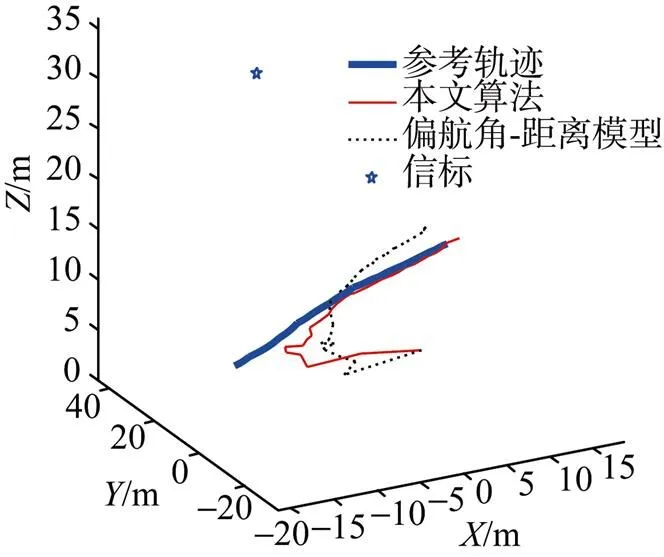
图1 仿真场景与定位结果

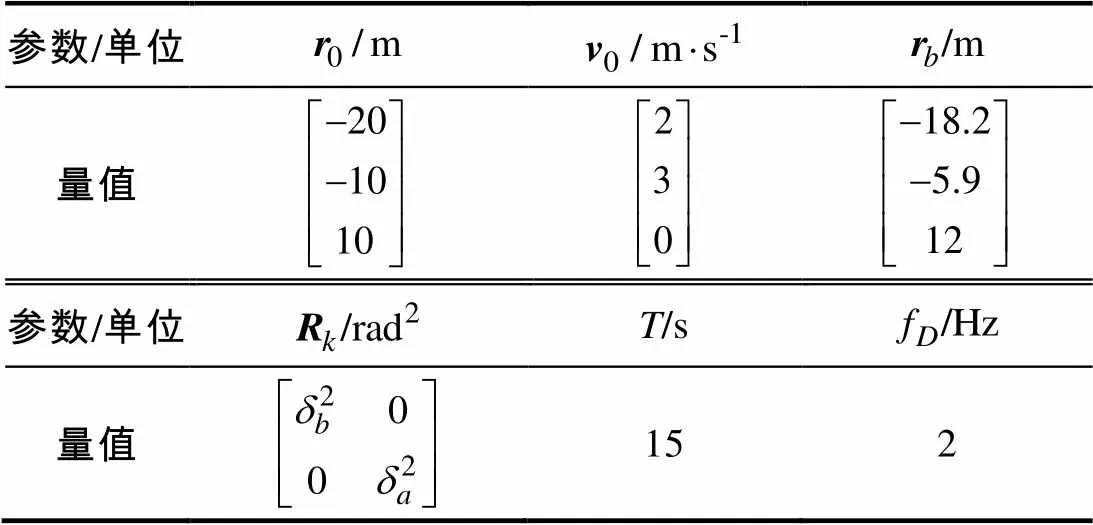
表1 自主水下航行器航迹初始状态及仿真参数

此处要说明的是, 由于实际中AUV自身推算误差累积导致在位置上容易出现较大误差, 而速度信息一般可利用AUV搭载的测速设备(多普勒计程仪等)获得, 故上述初值中根据这一事实进行了设置。

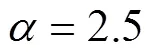
同时可以注意到, 速度误差呈现上升趋势, 这是由于文中不考虑导航问题, 为便于仿真验证, 载体姿态是依赖于速度解算出来的, 而仿真过程中, 速度除了在初始时刻都是未知的, 且根据前述可观测性分析可知, 目标位置本质上是通过方位和深度确定的, 从而速度的不确定性影响了方位的解算和目标位置估计, 因此速度实际上是不可观测的。而在实际应用中, 姿态可由AUV惯导设备获得, 此时速度误差和空间方位不是耦合的, 即能够对位置和速度进行修正。

图2 AUV运动状态估计误差(sd=10 m)

图3 AUV运动状态估计误差(sd=5 m)

图4 AUV运动状态估计误差(sd=1 m)

3 结束语

文中提出了一种在信标深度已知条件下, 基于信标纯方位信息的AUV定位方法, 构建了2-DOF姿态的AUV定位问题模型, 采用EKF进行求解, 并针对估值滤波器的选择及调参方法进行了分析, 通过仿真分析对所提出方法进行了验证, 并将其与现有基于测距信息观测模型的方法进行对比分析, 结果表明, 文中方法在滤波精度和收敛性上具有优势。需要指出, 由于文中重点考查提出方法的性能, 因此AUV的姿态是在无横滚平移假设下根据速度求得, 而非实际中通过航位推算过程得到, 下一步工作应结合AUV自身导航过程, 融合角度信息进行修正, 并采用实测数据进行验证。

[1] 孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015, 34(3): 64-65.Sun Da-jun, Zheng Cui-e. Discussion on Development Trend of Underwater Acoustic Navigation and Positioning Technology[J]. Journal of Marine Technology, 2015, 34(3): 64-65.

[2] Alexander P S. The AUV Positioning Using Ranges from One Transponder LBL[C]//Proceedings of the 1995 MTS/ IEEE Oceans Conference. San Diego. CA, USA: IEEE, 1995.

[3] Vaganay J, Baccou P, Jouvencel B. Homing by Acoustic Ranging to a Single Beacon[C]//Proceedings of the 2000 MTS/IEEE Oceans Conference. Providence, RI, USA: IEEE, 2000.

[4] 曹俊, 郑翠娥, 孙大军, 等. 系数矩阵正定的单信标测距定位算法[J]. 电子与信息学报, 2017, 39(4): 981-988.Cao Jun, Zheng Cui-e, Sun Da-jun, et al. A Single Beacon Location Algorithm with Positive Definite Coefficient Matrix[J]. Journal of Electronics & Information Techno- logy, 2017, 39(4): 981-988.

[5] 曹俊, 郑翠娥, 孙大军, 等. AUV直线航迹下的单信标测距定位算法[J]. 哈尔滨工程大学学报, 2017, 38(5): 733-738.Cao Jun, Zheng Cui-e, Sun Da-jun, et al. AUV Positioning Based on Single-beacon Ranging in Straight-line Trajec- tory[J]. Journal of Harbin Engineering University, 2017, 38(5): 733-738.

[6] 张福斌, 张永清. 一种利用单信标修正AUV定位误差的方法[J]. 鱼雷技术, 2012, 20(1): 38-41.Zhang Fu-bin, Zhang Yong-qing. Correcting Localization Error with a Single Beacon for AUV[J]. Torpedo Techno- logy, 2012, 20(1): 38-41.

[7] 曹方方, 刘卫东, 李娟丽. 基于EKF的UUV单信标水声导航定位方法研究[J]. 计算机测量与控制, 2011, 19 (9): 2234-2236.Cao Fang-fang, Liu Wei-dong, Li Juan-li. Navigating and Positioning Based on EKF for Unmanned Underwater Vehicle from A Single Beacon[J]. Computer Measurement & Control, 2011, 19(9): 2234-2236.

[8] Vallicrosa G, Ridao P, Ribas D. AUV Single Beacon Range-Only SLAM with a SOG Filter[J]. IFAC-Papers- Online, 2015, 48(2): 26-31.

[9] 严卫生, 房新鹏, 崔荣鑫. 单信标测距AUV水下定位系统观测性分析[J]. 中南大学学报(自然科学版), 2012, 43(8): 202-207.Yan Wei-sheng, Fang Xin-peng, Cui Rong-xin. Observability Analysis of Single­beacon Underwater Localization of Autonomous Underwater Vehicle[J]. Journal of Central South Unive- rsity(Science and Technology), 2012, 43(8): 202-207.

[10] 曹俊, 郑翠娥, 孙大军, 等. 水下载体的声学定位系统测距误差分析[J]. 南京大学学报(自然科学), 2016, 52 (5): 816-824.Cao Jun, Zheng Cui-e, Sun Da-jun. Ranging Error Anal- ysis of Acoustic Positioning System for Underwater Vehicle[J]. Journal of Nanjing University(Natural Science), 2016, 52(5): 816-824.

[11] Civera J, Davison A J M M. Inverse Depth Parameterization for Monocular SLAM[J]. IEEE Transactions on Robotics, 2008, 24(5): 932-945.

[12] Matsebe O, Holtzhausen S, Kumile C M, et al. Modeling the Kinematics of an Autonomous Underwater Vehicle for Range-Bearing Simultaneous Localization and Mapping [C]//International Conference on Mechatronics and Mach- ine Vision in Practice. Auckland, New Zealand: IEEE, 2009.

[13] Becker C, Ribas D, Ridao P. Simultaneous Sonar Beacon Localization & AUV Navigation[J]. IFAC Proceedings Volumes, 2012, 45(27): 200-205.

[14] Chaffield B. Fundamentals of High Accuracy Inertial Na- vigation[M]. Reston: AIAA Inc, 1997.

[15] PereaL, How J, Breger L. Nonlinearity in Sensor Fusion: Divergence Issues in EKF, Modified Truncated SOF, and UKF[C]//Proceedings of AIAA Conference of Guidance, Navigation, and Control. South Carolina, USA: IEEE, 2007: 3489-3499.

[16] Auger F, Hilairet M, Guerrero J M, et al. Industrial App- lications of the Kalman Filter: A Review[J]. IEEE Trans- actions on Industrial Electronics, 2013, 60(12): 5458- 5471.

[17] Gibbs, Bruce P. Advanced Kalman Filtering, Leastsqu- ares and Modeling: a Practical Handbook[M]. Pennsyl- vania. US: John Wiley & Sons, Inc., 2011.

[18] Hidalgo F, Bräunl T. Review of underwater SLAM techni- ques[C]//International Conference on Automation, Robot- ics and Applications. Queenstown, New Zealand , IEEE, 2015: 306-311.

[19] Paz L M, Tardós J D, Neira J. Divide and Conquer: EKF SLAM in O(n)[J]. IEEE Transactions on Robotics, 2008, 24(5): 1107-1120.

(责任编辑: 杨力军)

Underwater Localization Method of AUV Based on Single Beacon Bearing-Only Measurement

LI Jia-tong, ZHANG Chen, ZHANG Hong-xin

(91439thUnit, The People’s Liberation Army of China, Dalian 116041, China)

Under the condition that the depth of a beacon is known, a real-time positioning method of an autonomous undersea vehicle(AUV) is presented based on single beacon bearing-only information measurement to solve the problem of single beacon AUV underwater localization. Different from the traditional method based on single beacon ranging information, the coordinate transformation principle is adopted to construct a 2-degree of freedom(2-DOF) attitude AUV motion model, and a state space model of bearing-only AUV localization problem is derived under the condition of knowing depth. Based on the established models, the extended Kalman filter(EKF) is used to solve the problem, and a filter parameter adjusting method is presented for the application of EKF algorithm. The validity of the proposed method is verified by a simulation experiment. Comparison between the proposed method and the existing method shows that the proposed method based on single beacon bearing observation model is better in filtering accuracy than that based on ranging information, and its convergence performance is superior to that of the latter.

autonomous undersea vehicle(AUV); localization method; single beacon; bearing-only measurement; extended Kalman filter(EKF)

TJ630; TN953

A

2096-3920(2018)04-0310-06

10.11993/j.issn.2096-3920.2018.04.006

李佳橦, 张臣, 张宏欣. 基于单信标纯方位测量的AUV水下定位方法[J].水下无人系统学报, 2018, 26(4): 310-315.

2018-04-19;

2018-06-25.

李佳橦(1991-), 女, 硕士, 主要研究方向为水下无人系统定位技术.