波浪作用下圆柱型浮标运动仿真方法对比研究

杨壮滔, 张 涛, 段 浩, 朱 敏, 邵永勇



波浪作用下圆柱型浮标运动仿真方法对比研究

杨壮滔, 张 涛, 段 浩, 朱 敏, 邵永勇

(中国船舶重工集团公司 第705研究所昆明分部, 云南 昆明, 650118)

为研究圆柱型浮标在波浪作用下的运动响应, 分别采用基于势流理论和数值波浪水槽的浮标运动仿真方法对同一浮标模型进行仿真, 并与试验结果进行对比。结果表明, 对于垂荡运动, 2种方法的求解精度均较高。对于纵摇运动, 基于势流理论的方法预报规律趋势正确但定量误差较大, 其优点是所需计算资源较少, 可用于方案初步设计; 基于数值波浪水槽的方法求解精度较高, 但所需计算资源较多, 能够指导浮标精细化设计。

圆柱型浮标; 势流理论; 数值波浪水槽; 运动仿真

0 引言

圆柱型浮标在军用和民用领域的应用前景广阔, 但受海浪影响产生的运动会对其工作造成不利影响, 需要进行运动响应研究。由于垂荡运动和纵摇运动对浮标正常工作造成的影响最大, 因此这2种运动成为主要研究对象。1977年, 美国伍兹霍尔海洋研究所运用势流理论法, 研究分析了圆柱形浮标的垂荡和纵摇运动特性[1]。1994年, 哈尔滨船舶工程学院使用实验法对波浪作用下圆柱体的动态响应开展研究[2]。2010年, 西北工业大学对圆柱形浮标进行垂荡和纵摇运动特性研究, 得出对该型浮标的改进建议[3]。从前人的研究可知, 对浮标运动进行研究的关键在于波浪力的求解。莫里森(Morison)方程多用于求解固定圆柱在水流作用下的受力问题[4], 为了求解浮标运动过程中受到的流体动力, 需对Morison方程进行改进。

随着计算机技术的发展, 基于雷诺时均(Re- ynolds averaged Navier-Stokes, RANS)方法的数值波浪水槽在海洋工程领域得到广泛应用, 可用于开展圆柱型浮标在海浪激励下运动特性的研究[5]。

文章分别建立基于势流理论和数值波浪水槽的仿真方法, 使用2种方法对同一浮标模型进行仿真, 以垂荡运动响应和纵摇运动响应作为结果, 并以试验结果为依据进行对比研究。结果表明了2种方法能满足工程不同阶段的实际要求。

1 基于势流理论的仿真方法

1.1 坐标系建立

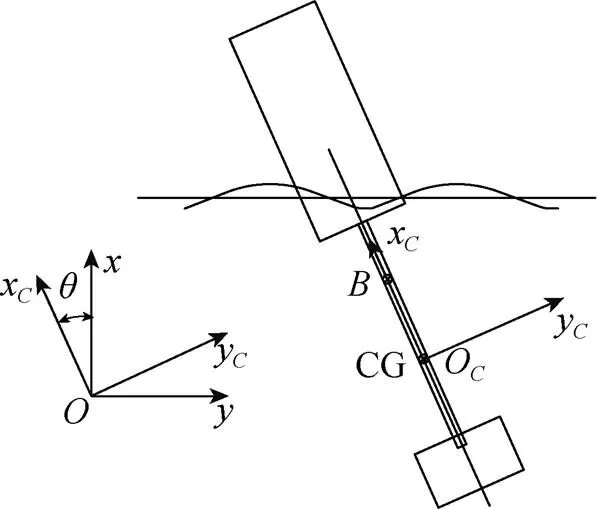
图1 圆柱型浮标坐标系

1.2 波浪方程

该方法选用线性波作为输入, 其波面呈现出简谐形式的起伏, 成余弦形式。水质点以固定的圆频率做简谐振动, 同时波形以一定的速度向前传播, 波浪的中线(余弦函数中线)与静水面相重合[6]。其波面方程和势函数为

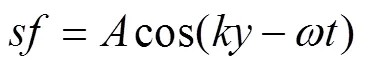
设浮标位于地理坐标系原点处, 将势函数对各方向求偏导, 得出水平方向水质点速度为

竖直方向水质点的速度为

再将速度对时间求导, 得出水平方向水质点加速度为

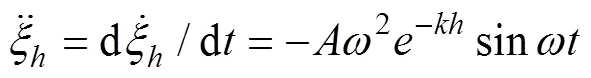
竖直方向水质点加速度为

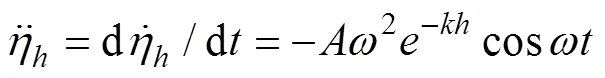
1.3 垂荡动力学方程

浮标在竖直方向受到重力、浮力、拖曳力和惯性力的作用[7]。根据动量定理, 在竖直方向上, 浮标的动力学方程可写为

经典的Morison方程只能求解沿固定圆柱体法向和切向的力[4]。但仿真过程中, 浮标相对于地理坐标系实时运动, 需要对经典的Morison方程求解进行改进。改进的基本思路为: 如图2所示, 分别将浮标和水质点相对地理坐标系的速度、加速度沿浮标的法向和切向进行正交分解, 通过速度、加速度的合成, 求解出流体动力沿浮标法向和切向的分量, 并通过正交分解求出浮标受到的力沿地理坐标系垂直方向的分量。

浮标受到的浮力为

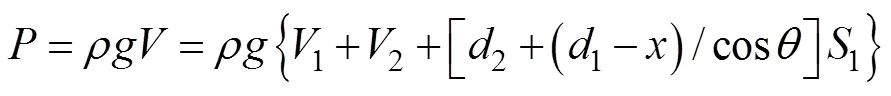
式中: 和分别为浮标没入水中舱段的排水体积; 为静止漂浮时重心到水面的距离; 为重心到浮标顶段底部的距离; 为水密度。

浮标受到的拖曳力为

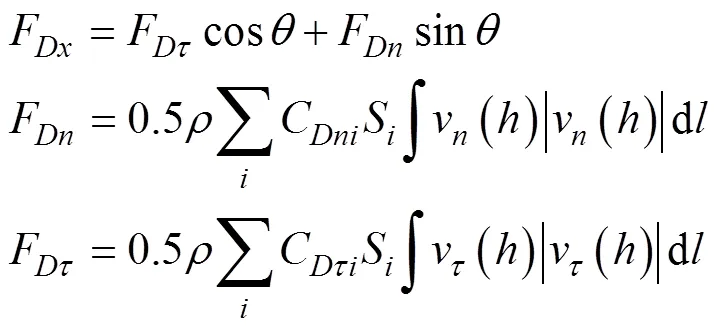
浮标受到的惯性力为

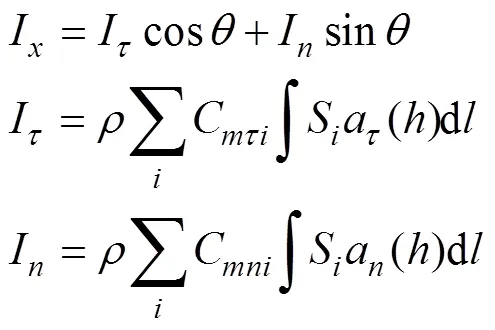
1.4 纵摇动力学方程

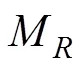
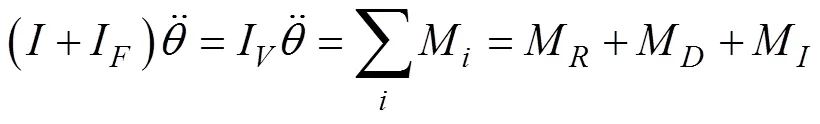
对各项力矩求解, 其中浮标所受回复力矩为

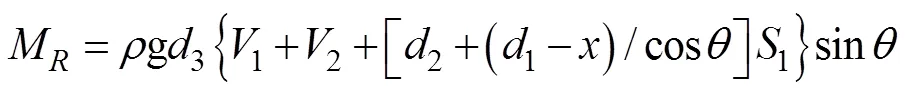
浮标受到的拖曳力矩为

浮标受到波浪的惯性力矩为

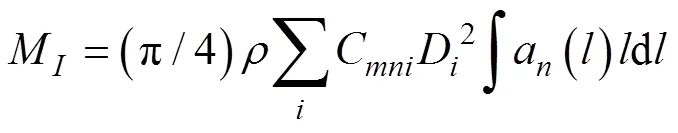
1.5 方程求解

将上文中求得的各项力带入式(7)中, 将各项力矩带入式(11)中, 将两式进行联立, 整理得

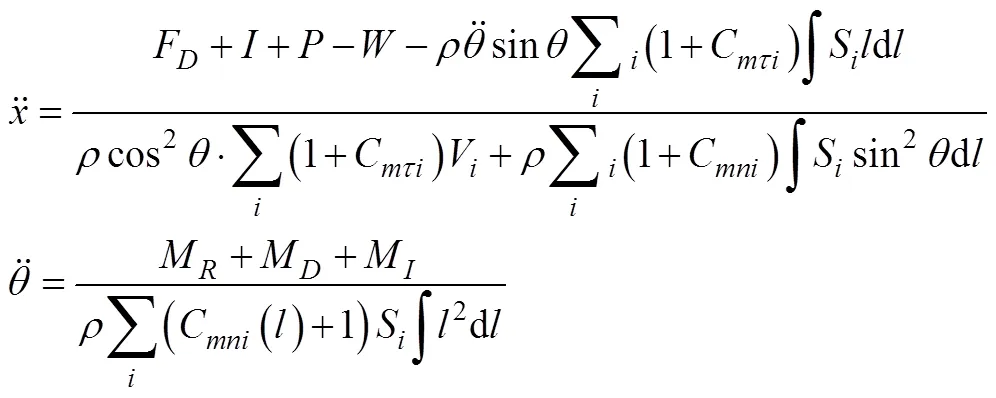
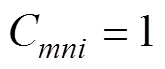
2 基于数值水槽的仿真方法

2.1 计算方程

该仿真方法使用的数值水槽以RANS方法和多相流模型为基础。RANS是目前工程上常用的计算流体力学(computational fluid dynamics, CFD)方法之一。其中, 空间离散采用有限体积法, 时间推进采用双时间法。该方法的连续性方程和动量方程可写为

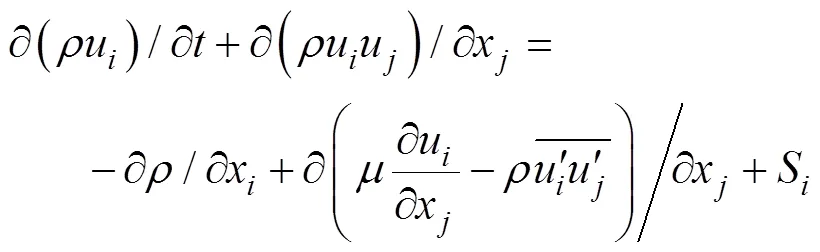
在数值造波时, 需要跟踪气体和液体的界面。因而选用流体体积函数(volume of fluid, VOF)方法处理气体和液体的界面跟踪问题, 该方法跟踪界面通过求解相连续方程实现[10], 方程为

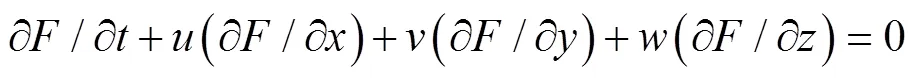
2.2 数值水槽造波

使用的造波方法为边界流体流动速度函数的直接输入法[11], 规则波波面方程和速度场在上文以给出, 表达式如式(1)~(6)所示。

随机波以波浪谱为输入, 使用傅里叶逆变换(inverse fast Fourier transform, IFFT)构造出有限波模态组成的波列进行随机波构造。使用JONSWAP谱生成随机波, 根据合田公式[12], 其能量密度

式中:

使用不需要阻尼消波区域的势流与粘流相结合的计算域来进行造波, 该计算域分为两部分, 分别为势流区域和粘流区域。如图3所示, 势流区域将粘流区域包裹住, 粘流区域在波浪传播方向的长度等于2个波长, 宽为1个波长, 浮标模型位于此区域。

图3 数值波浪水槽计算域示意图

2.3 6自由度模型

在计算过程中, 浮标姿态实时发生变化, 选用重叠网格法来实现计算中的浮标运动[13], 其原理如图4所示, 将不需要运动的背景网域设置为网格块1, 将需要运动的浮标重叠网格设置为网格块2, 通过交界面的差值来实现重叠区域和背景区域数值的交换。

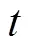
图4 重叠网格示意图

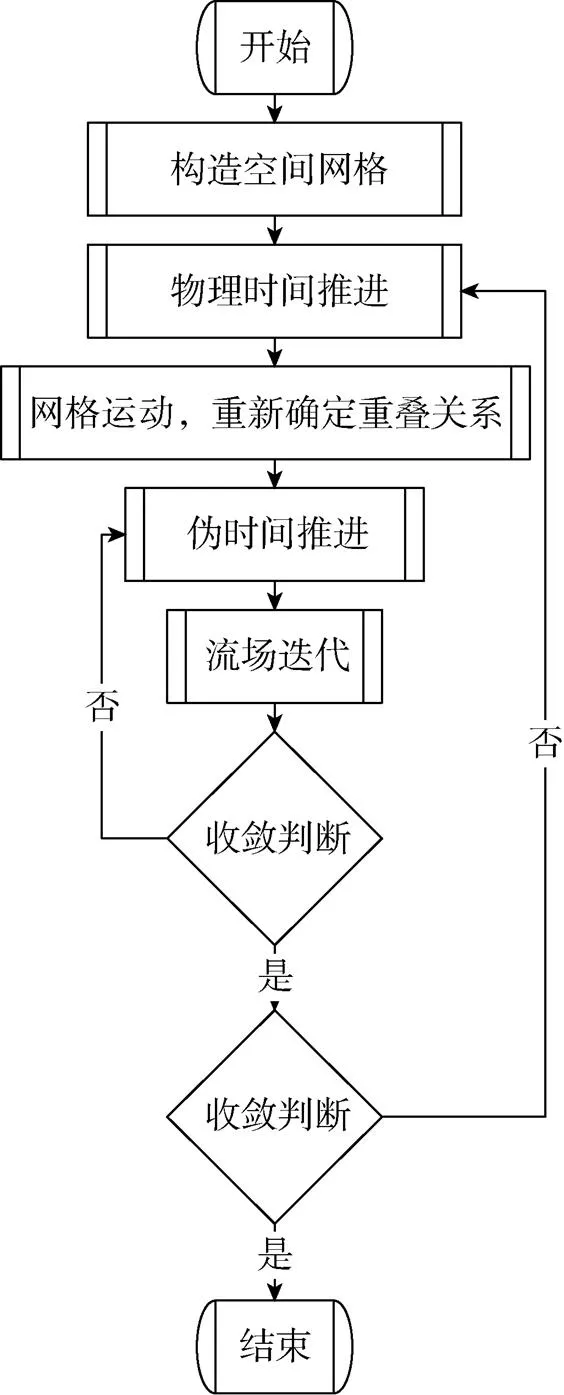
图5 重叠网格求解流程

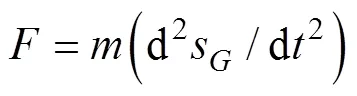
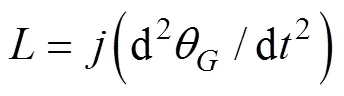
将式(20)和式(21)展开成3个方向可得

3 试验结果与分析

使用上文建立的2种仿真方法对浮标模型在波浪作用下的运动进行仿真, 并与试验结果进行对比, 分析2种方法在工程领域的适用性。

3.1 浮标模型

仿真模型外形和主要尺寸如图6(a)所示, 单位为mm, 物理参数如表1所示。试验所用浮标的外形尺寸参数与仿真中的浮标模型一致。模型如图6(b)所示, 由器件舱、浮囊和配重块构成。器件舱包含了用于测量姿态数据的陀螺仪、解算姿态信息的主控板和储存试验结果的SD卡。

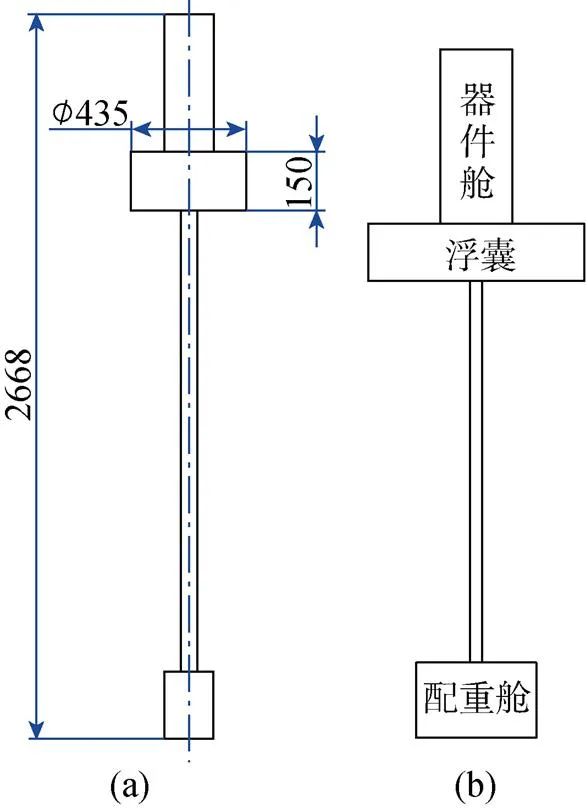
图6 浮标模型示意图

表1 浮标模型物理参数

试验分别在2级和3级海况下进行, 海况参数通过当地气象站得知。为了控制变量, 仿真时使用相同海况的数值波作为输入。海况波浪参数如表2所示, 使用的波高为有义波高, 即一列随机波中, 1/3的波高大于该值。

表2 不同海况下波浪参数

3.2 规则波作用下结果对比

使用规则波作为仿真输入, 该规则波使用有义波高和平均波长作为输入, 分别使用基于势流理论的仿真方法和基于数值水槽的仿真方法对浮标模型在规则波作用下的运动响应进行仿真。选取浮标运动稳定后70 s内的运动时励值作为运动响应结果。如表3所示为2种方法所需的计算资源和计算时间, 可以看出, 基于势流理论的方法占用计算时间和资源较少。如图7所示, 使用数值水槽法进行仿真时, 结果更直观, 更利于进行精细化仿真。

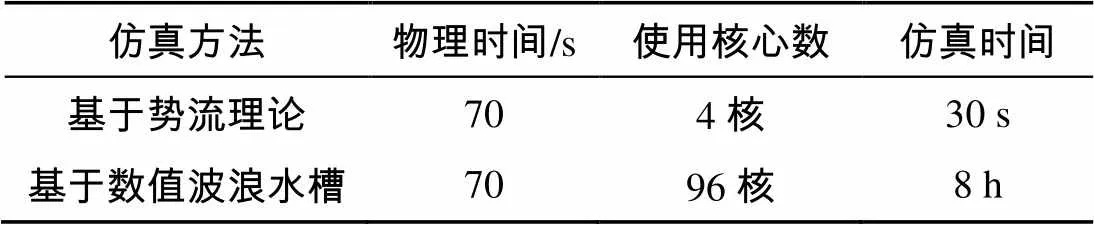
表3 仿真方法所需计算资源与计算时间

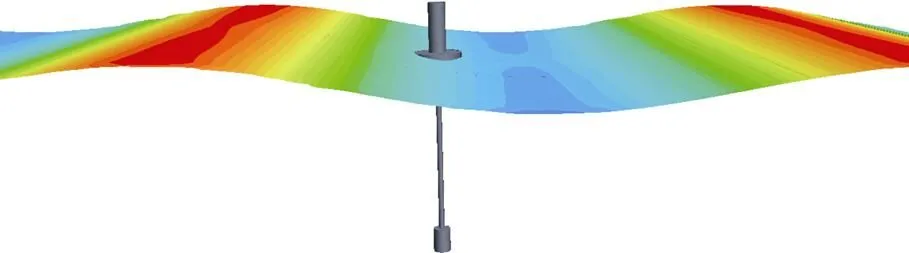
图7 规则波自由液面图

分别使用基于势流理论和数值波浪水槽的仿真方法得到的垂荡运动响应结果在1个坐标图中进行绘制, 进行对比分析, 如图8和图9所示。图中, 实线代表了基于势流理论的仿真方法求解得到的垂荡响应曲线, 虚线代表了基于数值水槽的仿真方法求解得到的垂荡响应曲线。2种方法得到的垂荡响应幅值和频率误差在5%以内, 且响应幅值与波浪幅值误差在5%以内。由此可得出浮标的垂荡运动受粘性效应的影响较小, 而受波面形状变化的影响较大。2种方法都能较为准确地仿真出波面方程, 因此得到垂荡运动的仿真结果误差均较小。

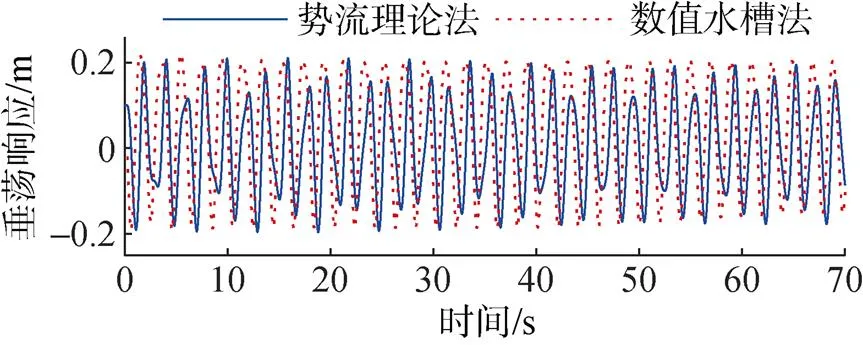
图8 2级海况下垂荡响应对比

图9 3级海况下垂荡响应对比

分别使用2种仿真方法得到的纵摇运动响应值与试验得到的纵摇运动响应值在一个坐标图中进行绘制, 进行对比分析。如图10和图11所示, 点划线代表了基于势流理论的仿真方法求解得到的纵摇响应曲线; 虚线代表了基于数值水槽的仿真方法求解得到的纵摇响应曲线; 实线代表了试验得到的纵摇响应曲线。基于数值水槽法仿真得到的纵摇响应幅值和频率与试验的有义值相比误差小于10%, 满足工程实际需求; 而使用势流理论法仿真得到的纵摇响应幅值和频率与试验的有义值相比误差较大。这是由于势流理论对流体的粘性效应进行了简化, 无法通过模型描述求解波浪遇到浮标后发生的绕射、越浪、破碎、爬高和涡旋等现象带来的影响[14]。

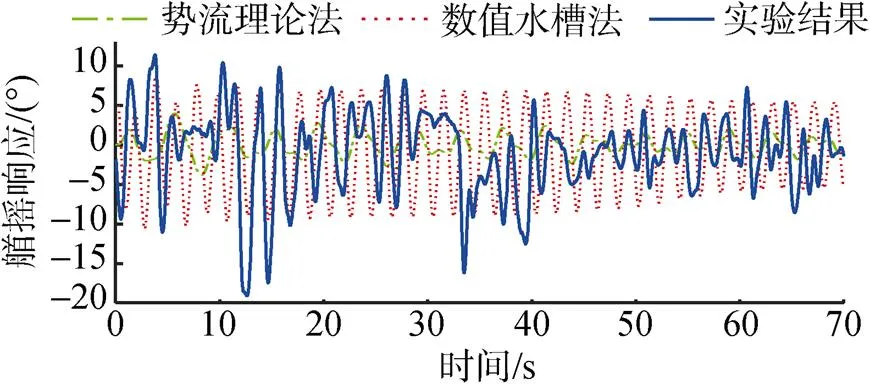
图10 2级海况下纵摇响应对比

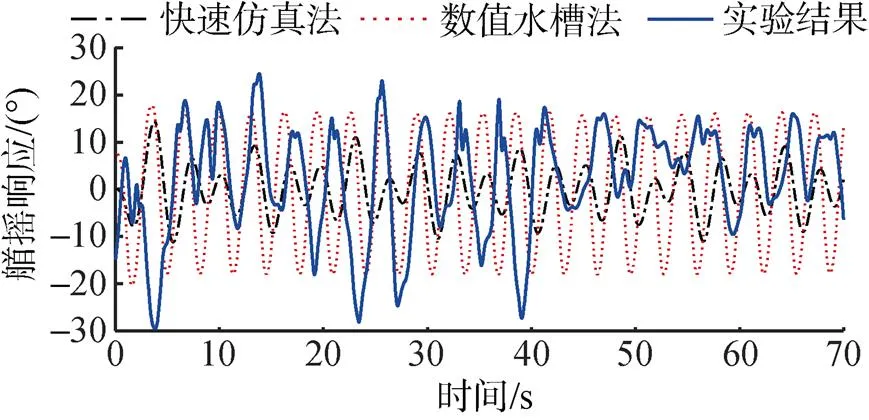
图11 规则波作用下3级海况纵摇响应对比

因此, 2种仿真方法得到的浮标垂荡运动响应结果精度较高, 而基于数值波浪水槽的仿真方法得到的纵摇运动响应结果精度较基于势流理论仿真方法的高。

3.3 随机波作用下结果对比

上文得出, 仿真得到的垂荡运动响应精度较高, 因此, 此节研究重点为以随机波为输入得出的纵摇运动响应。使用基于数值水槽的方法进行仿真, 选取浮标运动稳定后70 s内的纵摇运动时励值作为运动响应仿真结果。使用数值水槽法进行仿真, 海况波面图如图12所示。

图12 随机波自由液面

仿真得到的纵摇运动响应曲线与试验得到的纵摇运动响应曲线绘制在同一坐标图中, 进行对比。如图13和14所示, 虚线代表了基于数值波浪水槽的仿真方法以随机波作为输入, 求解得到的浮标模型纵摇运动响应曲线; 实线代表了试验得到的浮标模型纵摇运动响应曲线。由图中的对比可以得出, 仿真结果的纵摇运动的最大幅值、平均值幅值、幅值有义值与试验结果对比, 误差均小于10%, 证明使用数值波浪水槽的仿真方法所造的数值波浪符合波浪的自然规律, 能够较为准确的利用数学模型描述实际物理现象。仿真结果精度符合工程实际需求。

4 结束语

文中建立了基于势流理论的浮标运动仿真方法和基于数值波浪水槽的浮标运动仿真方法。将2种方法的仿真结果与试验数据进行对比分析, 结果表明: 1) 2种仿真方法得到的浮标垂荡运动响应结果精度较高; 2) 由于势流理论对浮标受到的粘性响应求解过于简单, 基于数值波浪水槽的仿真方法得到的纵摇运动响应结果精度较基于势流理论仿真方法的高。因此, 基于势流理论的方法预报规律趋势正确但定量误差较大, 其优点是所需计算资源较少, 可用于方案初步设计; 基于数值波浪水槽的方法求解精度较高, 但所需计算资源较多, 能够指导浮标精细化设计。

图13 随机波作用下2级海况纵摇响应对比

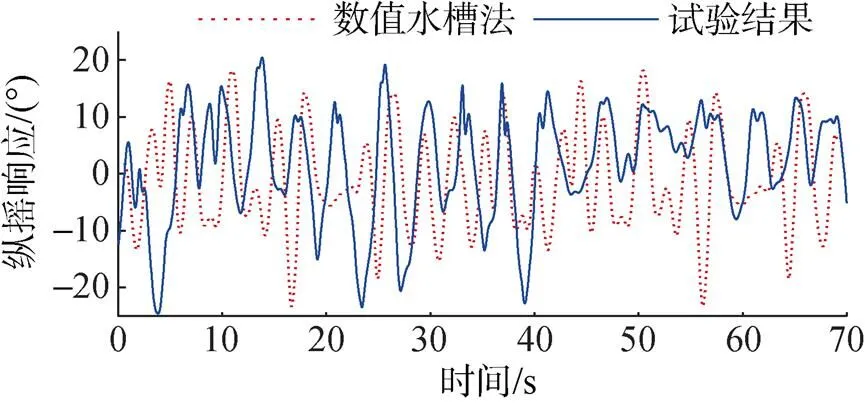
图14 随机波作用下3级海况纵摇响应对比

使用该2种方法研究并总结圆柱型浮标在波浪作用下的运动规律, 并为工程设计提供指导性意见将是下一步研究工作重点。

[1] Berteaux H O, Goldsmith R A, Schott W E. Heave and Roll Response of Free Floating Bodies of Cylindrical Shape[R]. US: Woods Hole Oceanographic Institution, 1977.

[2] 姚熊亮, 陈起富, 徐文景, 等. 圆柱在浪流联合作用下的动态响应[J]. 中国造船, 1994(4): 57-65.Yao Xiong-liang, Chen Qi-fu, Xu Wen-jing, et al. Dynamic Response of a Cylinder Under the Combined Action of Waves and Currents[J]. Shipbuilding of China, 1994(4): 57-65.

[3] 曲少春, 郑琨, 王英民. 圆柱形浮标运动分析与仿真[J]. 计算机仿真, 2010, 27(6): 363-367.Qu Shao-chun, Zheng Kun, Wang Ying-min. Analysis and simulation of Spar Buoy Motion[J]. Computer Simulation, 2010, 27(6): 363-367.

[4] Morison J R, Obrien M P, Johnson J W, et al. The Force Exerted by Surface Waves on Piles[J]. Petroleum Transactions. American Institute of Mining Engineers, 1950, 189: 149-154.

[5] 唐歆. 海洋资料浮标水动力分析及结构研究[D]. 上海: 上海海洋大学, 2012.

[6] 王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013.

[7] Hogben N. Wave Loads on Structures, Behavior of Offshore Structures(BOSS)[M]. Oslo: Norvegian institute of technology, 1976.

[8] Choo Young-IL, Mario J. Hydrodynamic resistance of towed cables[J]. Hydronautics, 1971, 5(4): 126-131.

[9] 马峥, 黄少锋, 朱德祥. 湍流模型在船舶计算流体力学中的适用性研究[J]. 水动力学研究与进展, 2009, 24(2): 207-216. Ma Zheng, Huang Shao-feng, Zhu De-xing. Study on Applicability of Turbulence Model in Ship Computational Fluid Dynamics[J] Chinese Journal of Hydrodynamics, 2009, 24(2): 207-216.

[10] Hirt C W, Nichols B D. Volume of Fluid(VOF) Method for the Dynamics of Free Boundary[J]. Journal of Computational Physics, 1981, 39: 201-225.

[11] 方昭昭, 朱仁传, 缪国平, 等. 基于数值波浪水池的波浪中船舶水动力计算[J]. 水动力学研究与进展, 2012, 27(5): 515-524.Fang Zhao-zhao, Zhu Ren-chuan, Miao Guo-ping, et al. Numerical Calculation of Hydrodynamic Forced for a Ship in Regular Waves Based on Numerical Wave Tank[J]. Chinese Journal of Hydrodynamics, 2012, 27(5): 515-524.

[12] Goda. A Comparative Review on the Functional Forms of Directional Wave Spectrum[J]. Coastal Engineering Journal, 1999, 41(1): 1-20.

[13] 赵发明, 高成君, 夏琼. 重叠网格在船舶CFD中的应用研究[J]. 船舶力学, 2011, 15(4): 332-341. Zhao Fa-ming, Gao Cheng-jun, Xia Qiong. Overlap Grid Research on the Application of Ship CFD[J].Journal of Ship Mechanics, 2011, 15(4): 332-341.

[14] 孙斌. 波浪作用下玻璃钢浮标水动力特性的数值分析[D]. 长沙: 长沙理工大学, 2011.

(责任编辑: 陈 曦)

Comparative Study on Motion Simulation Methods of Cylindrical Buoys under Wave Action

YANG Zhuang-tao, ZHANG Tao, DUAN Hao, ZHU Min, SHAO Yong-yong

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

To study the motion response of cylindrical buoys induced by waves, the same buoy model is simulated by using two buoy motion simulation methods based on respective numerical wave sink and potential flow theory, and the results are compared with the sea trial data. Comparison shows that: 1) both methods have high solution accuracy for heave motion; 2) for the pitch motion, the method based on potential flow theory gives a correct prediction trend but with low accuracy, however, this method has the advantage of requiring less computing resource, so it can be used for preliminary design of the program; and 3) the method based on numerical wave sink has high solution accuracy but requires more computational resources, so it can used to guide fine design of buoys.

cylindrical buoy; potential flow theory; numerical wave sink; motion simulation

TJ67; TV131.2; TP391.99

A

2096-3920(2018)04-0291-07

10.11993/j.issn.2096-3920.2018.04.003

杨壮滔,张涛,段浩,等.波浪作用下圆柱型浮标运动仿真方法对比研究[J].水下无人系统学报,2018,26(4):291-297.

2016-11-19;

2016-12-18.

杨壮滔(1993), 男, 在读硕士, 主要研究方向为水中兵器总体设计.