浅谈桥梁结构优化设计

(上海同豪土木工程咨询有限公司 上海 200082)

安全适用，经济美观和桥梁结构稳定不仅是桥梁结构设计的目的，对其也相当重要。1960年开始，桥梁结构的优化设计在世界范围随着建设的崛起而出现，1970年～1980年，我国桥梁的结构优化理论也就是在这期间发展起来了的。现在所采用的优化理论，是从两个方面来说的，整体和部分。把给定的安全系数的容许应力作为基础来建立起来，其中钢桥在这方面发展是最为好的，而对于混合材料的复杂结构则是很难以得到适用的，基于现代设计理论的发展，半概率、近似概率及全概率设计法都是在可靠度理论的容许应力下逐渐发展的，依靠可靠度的桥梁，其结构优化设计也是因此开始发展起来的，这是在设计思想和理论两个方面的一大飞跃[1]。

一、桥梁结构优化设计现状

桥梁多数是超静定结构或者是高次超静定结构，桥梁的内部构造是相当复杂的，并且在建设初期，桥梁设计阶段时要综合各方面因素比如几何尺寸、材料、参数等，这样就会使桥梁结构整体优化不太容易解决。故桥梁构造的优化设计基本是以部分优化为主，即便如此，桥梁结构是以整体优化为主体评价的，部分优化对整体效果的改善在一定程度上来说，是很难确定其优劣的，即便对整桥的所有单个构件进行优化，但是对整体而言却是很难去达到最理想的效果。

优化算法的定义就是寻求最优解的方法，目前已经出现了多种方法，大概可分为下面几种：数学规划法、最优准则法和仿生学法三种。这几种方法都是各有优缺，11数学规划法其优点是理论基础非常严格，在适宜的条件下会得到最好的结果，但其缺点是它需要问题能够明确表现出来，而且大部分的设计变量都要求是连续的、目标与约束函数连续且性态良好，但结构的优化问题是难以解决的，特别是对许多大型结构来说；22最优准则法是在以实际工程经验、度力学的理解和数学规划作为最优性条件，通过事先建立某种规则[2]，其收效高，计算速度快，但是通过相应的迭代方法获得最优或近似最优解，其使用范围较小；33仿生学法主要是以遗传算法、模拟退火法和神经网络法为主，其解题能力很强、应用的范围很广，可以在连续变量或整体变量、离散变量中应用，有的也可以用在非数值型变量，所以在近些年中发展很快[1]。

二、结构体系可靠度的基本理论及方法

相对于一个独立的构件或独立的截面可靠度来说，其极限状态可理解为其中任何一种出现失效模式(如拉压破坏、剪切破坏、失稳破坏等等)，但是在工程桥梁中，某一个桥梁构件也许会同时出现多种失效模式，如果其中任何一种失效模式存在，都极有可能会造成整个桥梁体系不作用。此外，桥梁的结构体系的组成方式主要有下面几种：串联、并联和混联(由串联、并联结合而成)，但是对于某一种较为复杂的结构体系而言，当某一个构件不作用时，却不一定会使整个结构体系损坏。故桥梁体系的可靠度研究可划定为多个功能函数的研究问题。

(一)结构体系可靠度分析方法

桥梁结构的可靠度分析方法主要有两种：一般可靠度分析法和时变可靠度分析法。一般可靠度分析法就是用结构设计可靠度的分析方法，这种方法不需要考虑外界环境对抗力的作用，也就是把结构内部的抗力视为不会因时间变化而变化的参量，从而能够用一次二阶矩的方法来计算，验算点法便是我们进行可靠度分析时用的最多的一种方法。时变可靠度分析法就是考虑结构在使用期间随时间的变化，耐久性损坏、承受荷载(交通量及荷载等级)而不断变化的可靠度分析过程[3]。

结构构件关于可靠度的分析方法主要有下面几种：一次二阶矩法、验算点法、蒙特卡罗法、响应面法、随机有限元法等[3]。

1.一次二阶矩法

一次二阶矩法的意思就是针对以结构的功能函数为变量的一次二阶函数，在以一阶矩与二阶矩的变化量，以此作为概率方式而进行可靠度计算的一种方法。应用一次二阶矩法的特点是仅仅只有抗力作用F和荷载效应S，由此方式求解出可靠度指标解析式，这些公式在实际工程中采用很多，也较灵活方便。

2.验算点法

Hosafer-Lind可靠度指标可以很精确地描述结构的可靠度，但其缺点是要求所有随机变量都得服从正态分布，这就与工程实际设计中的状况有所冲突，针对这一情况，就可以应用验算点法，其意思就是将非正态的变量近似看作为正态化，所替代的正态分布函数要求在设计点处的概率分布函数和概率密度函数值都要和原变量值相等[4]。当量正态化后，运用改进过的一次二阶矩法来得出桥梁结构的可靠指标。此方式可用于求解任何变量下的不同结构可靠度指标，运用此方法不仅是因为其基本思路清晰明了，运算过程方便操作，还因为其对非线性程度不高的结构功能函数所计算得出的结果精度是可以满足现实工程需要，因而被国际上许多机构所运用。

3.蒙特卡罗法

蒙特卡罗法也叫做为随机模拟法，有时也叫做为随机抽样方法或统计实验方法，其基本原理就是建造一个概率模型或者是设立一个随机的过程，使某一个参数等于所需的解，然后对这个模型或这个过程进行试验，来对所求得的参数进行数据特点统计分析，最后来求出相似解。

三、桥梁结构体系可靠度的优化分析

(一)结构可靠度研究方法

桥梁的结构体系可靠度优化，就是在已经确定的整体可靠度指标下，根据已知的目标函数，由全部到部分，来对构件的可靠度进行准确合理的分析，最后再从单一构件到整个结构体系来验算整体可靠度及目标函数的过程[5]。

(二)优化模型

如果其中一个桥梁结构B由m个单元构件B1,B2…Bm组成，以全部经济费用为确定函数，整体可靠度为管束条件来建立一定的数学规划:

Findpi(i=1,2,…n)

MinW=∑Wi(pi)

StPA≥P*

上式中，W和Wi分别为桥梁整体和单独构件的经济费用：pi和P*分别为桥梁整体可靠概率和整体可靠概率要求[1]。

类似的这种模型在实际工程中就是要在确保全部可靠度的条件下来减少总体经济费用，尺寸和材料的费用与各构件的经济费用关联起的，而且尺寸和材料会影响结构的可靠度，因此我们常常用假定的方法来构建函数，也就是假定构件的经济费用为其可靠度的函数。

(三)整体可靠度验算

最优目标函数值及其各个构件的可靠概率是根据可靠度的约束优化模型中以某种假设或简化模型作为根据来求得的，不同结构或者相同结构之间的一些细节问题容易被忽略，包括关联性质、荷载信息，而且构件之间的可靠度概率是很难通过整体的可靠度概率来进行精确的推算来得到，而且求出的结果其精确度偏低，可能不会符合实际工程的要求，所以要更进一步的进行整体可靠度验算，如果两种方法共同进行，并逐步优化，就可使其得到最优解。

通常一个结构体系并不都是由串联、并联及两者的简单组合而构成，构件间大部都存在着一定的联系，尤其是当某个构件不能作用时就会出现内力重分配的现象，在虚拟或简化的计算条件下，得到的结果往往都需要再次或重复的调整和验证。假设有一个连续刚构，如图1所示，由构件1～5组成，从使用功能角度考虑，当构件1,2,3中有一个失效，结构就会因此失去交通能力，而构件4,5的失效在结构力学理论中的体系稳定性条件下不会引起上部结构失稳，体系结构简化如图2(a)的组成方式，而但当考虑内力重分布和材料承载能力时，构件4,5中有一个失效或全部失效时就可能会造成上部结构的失效，体系结构可分别简化成如图2(a).(b)所示的组成方式。因此可以看出，实际结构的简化常常带有不确定性，使用图2(a).(b)所示的简化方式计算出的结果并不一样，这时结构整体可靠度的验算和局部构件可靠度的调整是非常必要的，而且往往需要结合有限元、有限差分等进行更进一步的数值求解来作为失效的判断[5]。

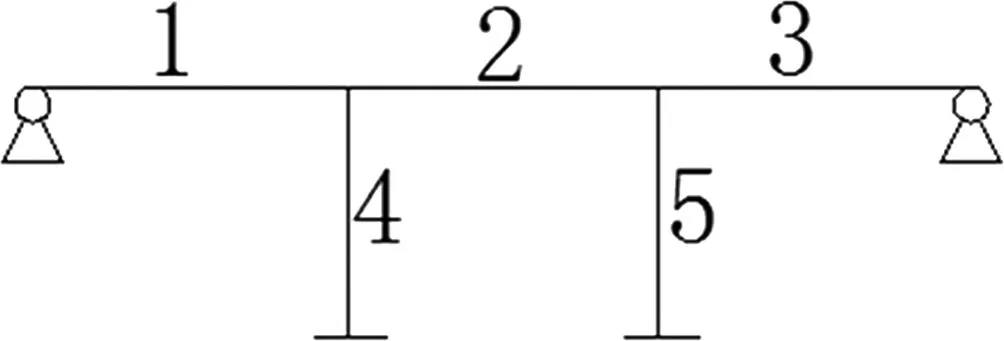
图1 连续刚构桥组成示意

图2 可靠度体系组成方式简化示意图

四、结语

桥梁的结构可靠度评定的工作量是难以进行评估的，短期内完成的可能性不大，因而本文的内容有许多不足，只能仅仅作为一项参考辅助研究，还需更进一步的完善。

11截至现在所存在的优化理论和可靠度理论的体系有了一定的效果，但结构的整体可靠概率到局部构件的可靠概率的反算、参数改变及部分无作用时会引起的结构内力重分布问题、构件间的相关性问题、实际工程结构的组成方式等问题依旧是桥梁结构可靠度优化分析上亟待解决问题。

22明确结构体系及其内涵，剖析桥梁结构体系的受力状况、传力途径和设计参数等之间的影响，可以为合理选择桥梁结构体系明确方向，也可寻找出桥梁结构体系创新的方法。

33体系创新对于优化结构受力、减少建设投资、提高施工方便、减少养护费用，进而满足工程需要，扩展桥梁适用的工程条件具有十分重要的意义

桥梁在运营期内必然会承受各种荷载，且易受风、雪、雨、地震等外部因素的影响。它们的可靠性将与人民的生命财产安全直接挂钩；此外由于设计、施工因素和运营期中都会有许多不确定因素；所以其可靠度分析是必然要有的，这样才能保证桥梁结构在设计时间内成功完成任务。