山丘区小流域洪水风险模型研究及应用

李晓英，谈亚琦，苏志伟，田佳乐

(1.河海大学 水利水电学院，南京 210098； 2.杭州诚禹水利科技有限公司，杭州 310008)

为预防和减轻洪水带来的危害，抵御洪水侵袭，研究洪水演进的规律显得十分重要。随着计算机科学的不断进步，越来越多的洪水演进模型得到开发研究，成为防洪减灾理论体系的组成部分和分析工具。

洪水演进数值模拟是研究洪水演进规律的有效方法之一。Caleffi等人[1]采用二维浅水方程对意大利托切河进行洪水演进模拟。Bladé E等人[2]基于有限体积法分别建立一维、二维水动力学模型，并提出基于数值通量的耦合方法，加强一维～二维模型之间的动量传递，在位于西班牙的埃布罗河进行验证；李传奇等人[3]利用构建的一维二维水动力耦合模型，针对不同典型降雨过程，对模型进行验证，并最终用于模拟济南市不同重现期下洪水淹没情况；苑希民等人[4]建立了一、二维水动力耦合模型，其中一维模型采用Preissmann格式离散，二维利用Roe格式离散，应用模型于黄河青铜峡河西灌区溃堤洪水的模拟，较为真实地反映了洪水在计算区域的演进过程与淹没范围；吴天蛟等人[5]以MIKE11为基础，区间入流采用分布式模型，对三峡库区进行洪水演进模拟；谢作涛等人[6]从求解Holly-Preissmann格式出发，结合有限差分法建立一维洪水演进模型；槐文信等[7]建立一、二维水动力学模型对渭河下游河道及洪泛区洪水进行数值仿真模拟；付成威等人[8]建立了一、二维实时动态耦合模型，并利用湿水深和干水深理论，改进传统洪水演进模型，将模型在谷堆圩蓄滞洪区进行了验证，结果良好。

基于上述研究，本文应用圣维南方程组作为一维模型的基本方程；应用水流运动的能量守恒原理和质量守恒推导得到平面二维非恒定流数值模型的基本方程组，进而得到二维水动力学模型。通过侧向连接的方式建立一维、二维耦合水动力学模型，利用该模型于太平溪山丘区小流域，对该流域作P=10%设计暴雨条件下的洪水演进模拟分析，为该区域防洪风险管理提供数据参考。

1 原理介绍[9-12]

1.1 一维洪水演进模型原理

以圣维南方程组为一维水动力学模型采用的基本方程。方程表示如下：

式中：Q为流量，m3/s；A为断面面积，m2；B为河道水面宽度，m；α为动量校正系数；g为重力加速度,m/s2。

1.2 二维洪水演进模型原理

根据水流运动的质量守恒以及能量守恒原理，可以推导出平面二维非恒定流数值模型的基本方程组，该方程组由连续性方程以及X、Y方向的动量方程组成：

式中：h为实际水深,m；η为水面高程,m；u、v分别为X方向和Y方向的流速,m/s；S为源汇项,m2/s；ρ0为水的密度,kg/m3；f为科式力系数；τsx、τsy分别为X方向和Y方向风切应力；τbx、τby分别为X方向和Y方向底部切应力；Tih为黏滞项、紊动项和扩散项的总和。

1.3 一维、二维模型耦合方式及模型求解过程

本文以侧向连解的方式完成一维洪水演进模型与二维洪水演进模型的耦合，耦合模型求解过程见图1。

图1 耦合模型求解过程Fig.1 Coupling model solving process

2 模拟实例[13-14]

2.1 区域概况

太平溪流域属于山川乡在安吉县的南部，该流域是苕溪流域的源头支流，安吉县境内区域受馒头山水库控制，控制范围内的集雨面积约为27.6 km2，河流长约为11.9 km。该流域所属区域包括安吉县山川乡大里村、九亩村、船村3个行政村，该区域在汛期来临时，天然来水量十分巨大且流速迅急，给该流域及其下游防护区安全造成极大的威胁。

2.2 太平溪流域流水网生成

在特定的流域，径流汇聚的多少与水流累积值成正比。因此，可用水流累积个数来定义河流的起始点。在河网生成的第一步中，必须先设置水流累积矩阵累积值的阈值，认为在水流累积个数小于该值的网格上不能产生足够的径流而形成水道，而大于该值的网格上能形成水道。由此，水流累积个数大于该值的网格所组成的流水网，即为一个栅格形式的河网，可称之为模拟河网。

当采用阈值来确定河网起始点时，由于流域地形、下垫面产流机制以及流域所处区域气候条件等因素的不同，其阈值也不同。本文基于DEM数据，生成了太平溪流域的模拟河网；采用自然流域分块的方法生成流域子单元，将太平溪流域分为6个子单元(图2)，其中子单元3、4、5位于太平溪的干流；子单元6位于上游；子单元1和2分别为区间入流。

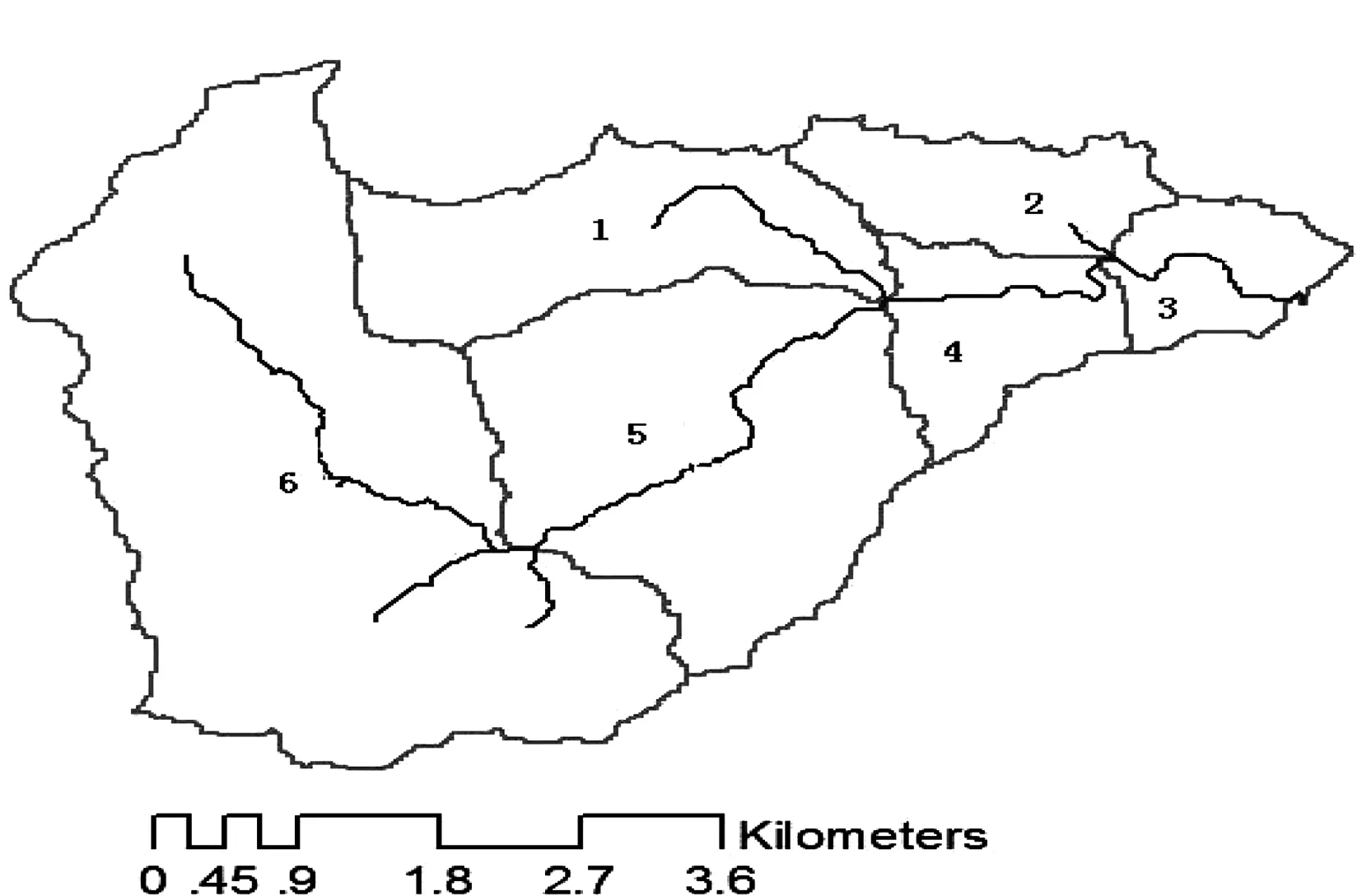
图2 太平溪流域模拟河网和划分子单元示意图Fig.2 A schematic diagram of simulating river network and dividing sub - unit in Taipingxi basin

2.3 太平溪流域网格划分

本文基于无结构网格来生成太平溪流域坡面二维洪水演进的计算网格。

二维洪水演进模型的边界可以分为开边界与陆地边界，开边界就是指流量过程、水位过程等人为设定一部分水体所形成的有界计算域；而陆地边界是指水流运动的边界，一般使用无滑移边界来设定，认为水流不能越过陆地边界。陆地边界是实际存在的边界。由于流域边界为山脊分水岭，一般水流不能越过分水岭，故本文以太平溪流域边界作为生成网格的陆地边界。此外，考虑到二维水动力模型需要与一维水动力模型进行耦合，故本文在生成网格时将太平溪干流区域也当作单独的边界进行处理。生成网格时，每个网格的最大面积限制在2 000 km2以内。生成网格后将太平溪内的高程信息插值至各计算网格，结果见图3。

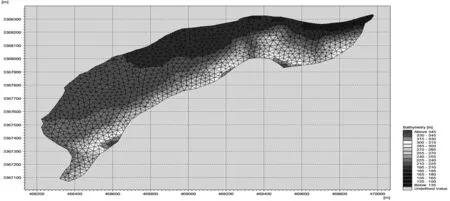
图3 太平溪流域二维洪水演进网格示意图Fig.3 Schematic diagram of two-dimensional flood evolution grid in Taipingxi basin

3 耦合模型构建

3.1 边界条件

二维洪水演进模型的边界条件包括两类：①水陆边界条件：此类边界条件为图4中二维洪水演进模拟范围的边界，认为水流无法越过该边界，在水陆边界法向处的流量及流速均为零。②流量/水位边界条件：此类边界条件为太平溪干流向流域坡面漫滩的过程。本文采用侧向连接的方式(图4)将一维太平溪干流与二维太平溪流域坡面进行耦合，利用堰流计算通过侧向连接的水流:

式中：q为交换水量，m3/s；W为宽度，m，一般取单元格和河道相连的边长；C为堰流系数；k为堰指数；Hus为堰上游水位,m；Hds为堰下游水位,m；Hw为堰顶高程,m。

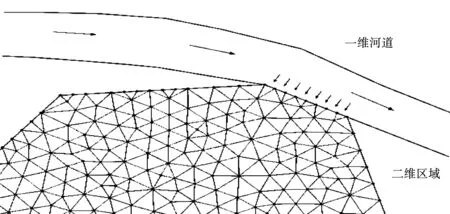
图4 侧向连接示意图Fig.4 Side connection diagram

3.2 动边界处理

由于洪水在流域坡面上运动的特殊性，计算区域中会存在随水位涨落而变化的动边界, 为保证模型计算的连续性, 采用干/湿处理技术来对动边界进行处理。其中，干水深设置为0.005 m，湿水深设置为0.07 m，淹没水深设置为0.05 m。即当计算区域水深小于0.005 m时，该计算区域记为“干”，不参加计算；当水深大于0.07 m时,该计算区域记为“湿”,重新参加计算。

3.3 初始条件及模型参数

在太平溪干流未发生漫滩时流域坡面上的积水较浅，本文假定此时区域内是无水的，认为初始水位为流域坡面的地面高程值。

由于缺少实测资料，各类地形、区域取值因地制宜，但大致保持在一定范围内。本文依据相关经验及相关文献各糙率值，确定为如下：一、二维的河道取值为0.03，村庄取值为0.07，水田取值为0.05，树丛取值为0.05，道路以及空地取值为0.035。

4 太平溪流域洪水淹没风险分析

选取P=10%频率下的50 h的设计暴雨，基于本文构建的耦合洪水演进模型对太平溪流域的洪水淹没风险进行分析。图5为P=10%设计暴雨条件下不同计算单元的出流过程。

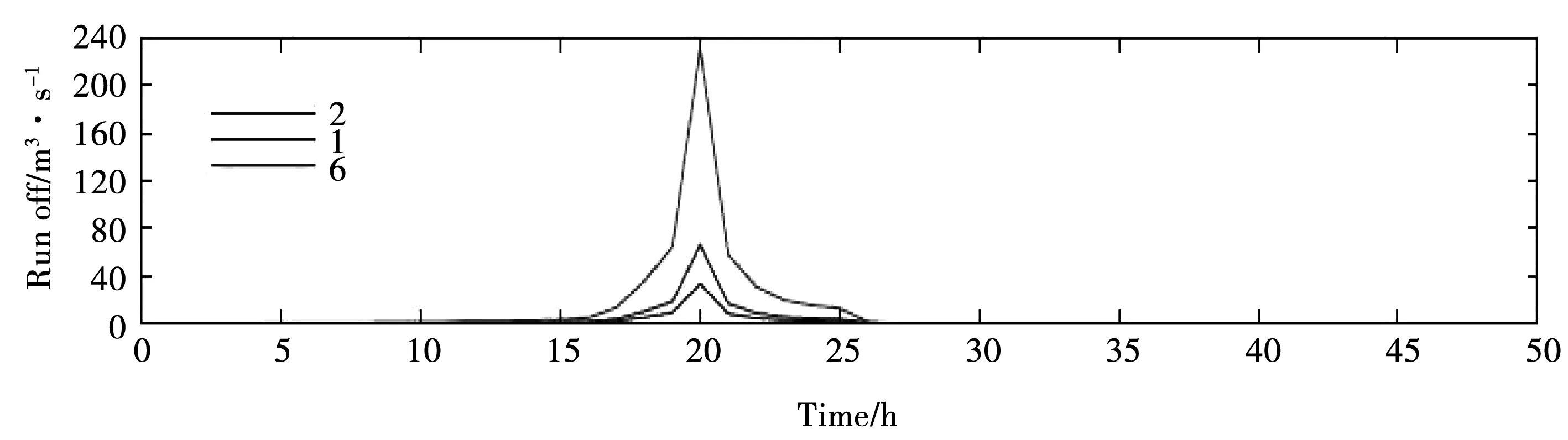
图5 太平溪流域P=10%设计洪水模拟过程 (子单元1、2、6)Fig.5 P=10% design flood simulation process in Taipingxi basin(subunit 1、2、6)

根据以上边界条件模拟了洪水太平溪干流及坡面上的演进过程。图6为太平溪干流在P=10%时最高水位的沿程分布情况，最高水位出现在第20 h，也即边界入流达到峰值的时刻。从图6可以看出，太平溪干流大多数断面所面临的风险情况较小，水位均在干流主槽内，未发生漫滩的情况。但仍有3个断面发生了漫滩的风险事件，这3个断面位置见图7，其计算起点距分别为1 913.4、3 044.9和3 676.7 m。

图6 太平溪干流P=10%最高水位分布Fig.6 P=10% maximum water level distribution in Taipingxi mainstream

图7 太平溪干流P=10%发生风险事件断面示意图Fig.7 P=10% risk profile schematic in the Taipingxi basin mainstream

图8～图11分别为设计暴雨时间内35 h的太平溪流域坡面淹没的范围及深度示意图。从这些图可以看出，由于漫滩事件的发生，从设计暴雨的20 h起洪水由太平溪干流进入流域坡面进行传播，发生淹没的区域位于风险断面2，并造成太平溪流域船村的风险事件。但在P=10%设计暴雨条件下，洪水淹没的范围相对有限，主要集中在干流附近，并且主要向下游方向进行演进，未对船村造成过大的影响。从淹没发生的时间过程来看，发生漫滩事件后2 h(图9)的淹没深度达到最大值，随后随着洪水的扩散与归槽，淹没深度逐渐减小，发生漫滩事件后10 h后的淹没高程已显著降低。

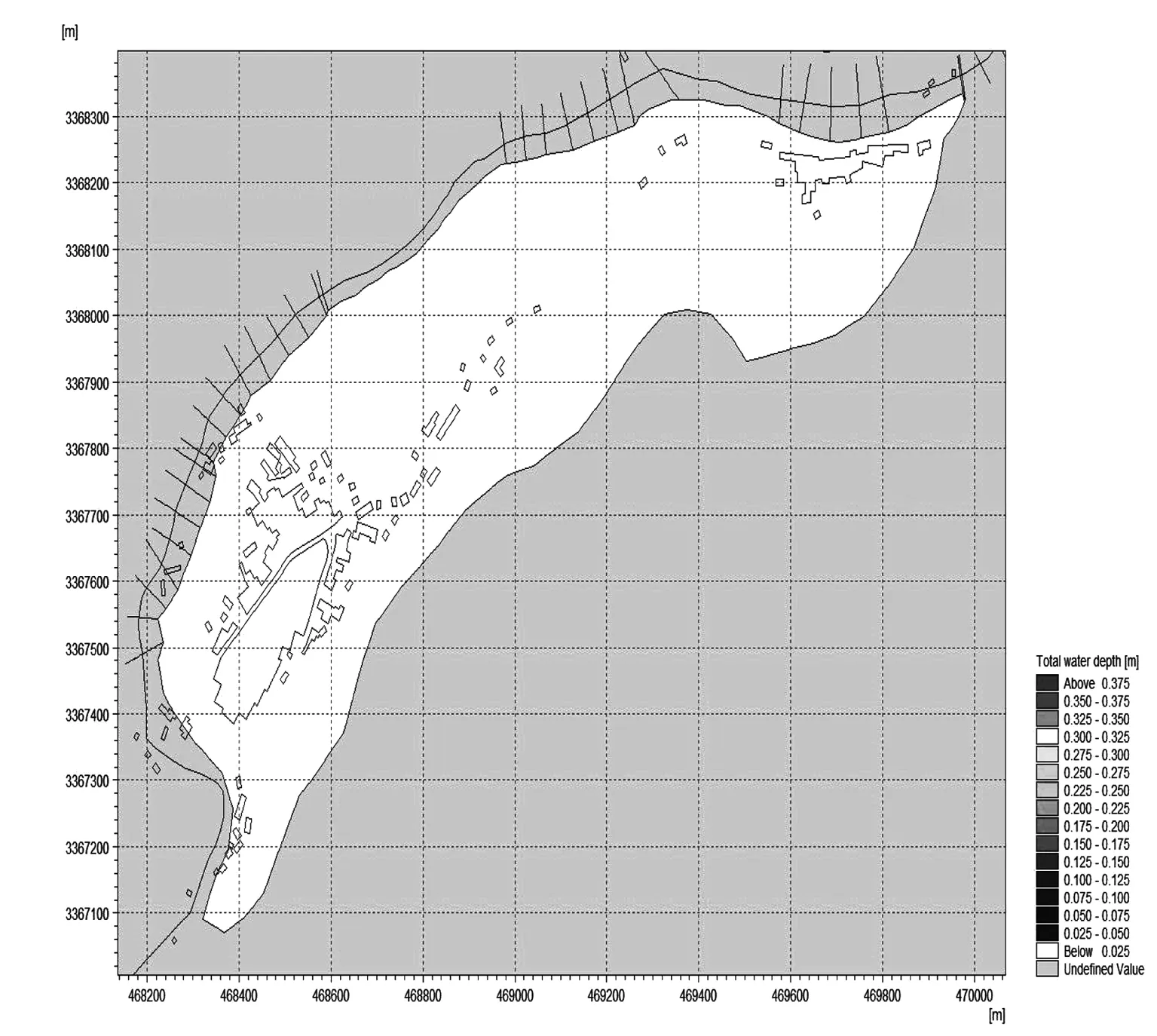
图8 太平溪流域淹没范围及深度示意图(19 h)Fig.8 Flooding scope and depth schematic in Taipingxi basin(19 h)

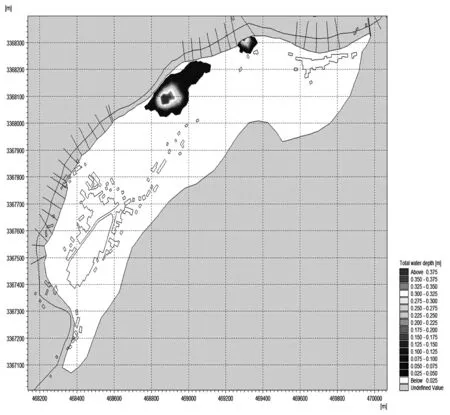
图9 太平溪流域淹没范围及深度示意图(22 h)Fig.9 Flooding scope and depth schematic in Taipingxi basin(22 h)

图10 太平溪流域淹没范围及深度示意图(25 h)Fig.10 Flooding scope and depth schematic in Taipingxi basin(25 h)

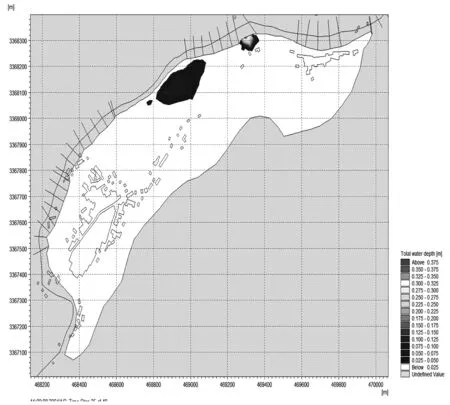
图11 太平溪流域淹没范围及深度示意图(35 h)Fig.11 Flooding scope and depth schematic in Taipingxi basin(35 h)

通过对比设计暴雨过程、径流过程以及淹没过程发现，由于太平溪流域的汇流时间较短，故暴雨中心到洪峰的时间以及漫滩风险发生的时间均较短，在P=10%设计暴雨条件下的时间仅为1 h。为此，需要建立洪水预报警报系统。通过将实时降雨、水文等数据输入模型得到预报信息，在必要的情况下，启用警报系统，为抗洪救灾、居民撤离等提供宝贵的准备时间，减少经济损失。

从工程措施来看，通过提升3个风险断面的堤防可以防止漫滩事件的发生。具体来说，风险断面1加高5 cm、风险断面2加高15 cm、风险断面3加高20 cm。通过数值实验分析发现，在加高以上3个断面的高程后，太平溪流域在P=10%设计暴雨条件下无风险事件发生。

5 结 语

1) 基于DEM数据生成太平溪流域的模拟河网，基于无结构网格生成流域坡面二维洪水演进的计算网格，以侧向连解方式完成一维洪水演进模型与二维洪水演进模型的耦合。

2) 利用建立的耦合模型对太平溪流域P=10%设计暴雨条件下的洪水淹没进行分析，并根据分析结果，为山丘区太平溪流域提出风险应对对策及工程和非工程措施。

3) 采用基于数学模型技术的洪水过程研究，可以准确地分析流域的洪水过程特征和洪水风险因子，利用耦合模型进行洪水风险分析研究将成为洪水风险管理的一项重要的技术支撑。