基于BP神经网络的井下机电节能研究

张跃辉

(山西新村煤业有限公司,山西 长治 046000)

在井下机电设备中,以井下掘进机电气设备耗电量为最大,此类设备中,大功耗电气设备有电力变压器、电动机、带式输送机和掘进机四种。而电力变压器又是输电网络中的主要设备,是电力安全传送的重要保障。随着井下供电需求的增加,电力变压器容量越来越大,其带来的能量耗损问题也日益凸显。电力变压器的能量耗损主要是运行过程中的空载和负载,二者均可由试验获得。实际生产中,既要保证低空载损耗,还要降低负载损耗,这就要求统筹优化好两者之间的比例。

20世纪70年代,奥地利学者计算变压器电流时忽略了集肤效应,然后从其它方面提高了算法精度;随后的德国科学家,在忽略集肤效应的基础之上,又建立了变压器中各个参数在不同频率影响下转换的数学模型,依次优化各个参数[1]。传统的BP神经网络中使用的是常数学习率,本文拟从均方误差与权值的角度出发,每个迭代步产生误差后都进行调整,即对各层的权值进行动态调节,此法亦称为自适应步长法。具体来说就是用随机选择的归一化样本来训练和预测方法，预测井下掘进机的电压。当求得预测值与真实值间的误差≤0.04,说明改进的方法有效。

2 神经网络原理

2.1 神经网络模型

人工神经网络简称ANN网络,是受动物神经网络结构启发,让要实现的原理或功能自己进行模拟和训练,即具备自学能力。人工神经网络单元与单元之间由权值连结,神经网络的好坏直接取决于权值[2]。选择不同的权值,得到不同的神经网络,其训练效果也不同。神经网络是由多个神经元组成,包括输入层、中间层、输出层,每个神经元在输入数据后都能输出单一的结果[3]。按照拓扑结构的分类原理,可将人工神经网络分为前馈型和反馈型。后者应用范围最广,但是也要求较高的计算能力和反馈调节能力,结构也较前者复杂。神经网络训练方法,是每次迭代之后,权值都会根据记忆和自身优化能力进行调整。神经网络的稳定输出取决于网络内部结构的权值和输入数据。输入数据的随机性越大,误差越大。反馈型神经网络的缺点在于,网络训练的权值要朝着误差递减的方向进行训练,在这种情况下会产生一种伪状态(局部极小值),不能实现全局最优收敛。前馈型神经网络中,权值处理方向都指向数据输出方向,即方向单一。换言之,在神经网络方法训练过程中,各层神经元之间的权值是相互关联的,表示输入层和输出层间的关系,没有训练的神经网络,其权值就没有意义,所以该网络不能被用来预测数据[4],神经网络权值系统图见图1。

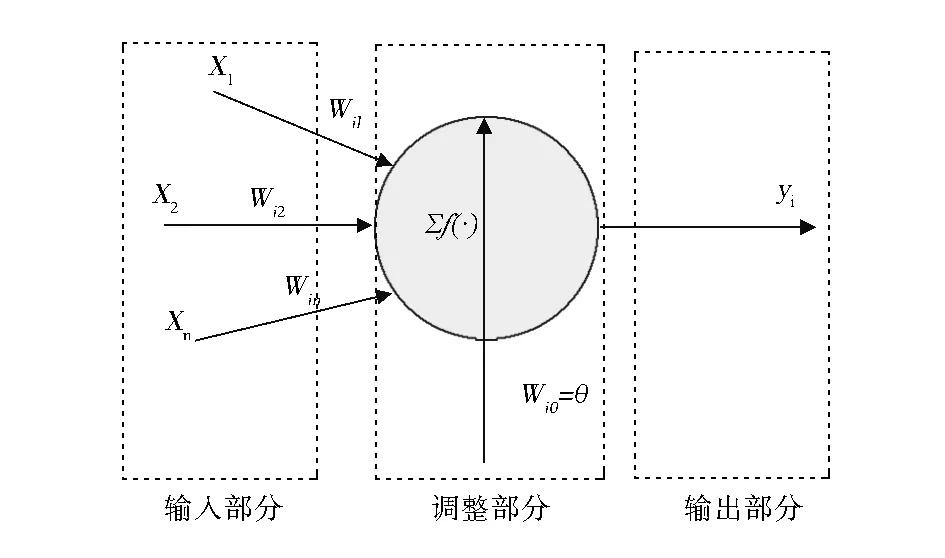
图1 神经网络权值系统图Fig.1 Weight system of neural network

本文拟选用前馈型神经网络中的经典算法——BP神经网络算法来预测电压。利用其单向的训练学习方法,可以将输入的预测数据从此神经网络中优化输出。

图1是神经网络的一个典型模型——多入单出的非线性模型。n表示数据输入个数，X表示系统输入信号，W表示权矢量，f(·)是激活函数。具体步骤如下：①训练样本X被作为输入信号输入，通过调整权系数W，得到相应的结果，然后输出；②把期望的数字信号当成训练的信号，与①中结果进行比较，得到误差；③用得到的误差去控制和修改权系数W。如果将上图输出结果记为u的话，则有：

u=∑WiXi=W1X1+W2X2+…+WnXn.

(1)

式中，i=1,2,…，n表示样本数。

用期望输出信号Y(t)和u对比,得到误差信号m,然后利用误差m沿误差减小的方向调整权值,直到满足系统设定误差。学习过程结束的标志是实际输出值u和期望输出值Y(t)无限逼近。

2.2 传统BP神经网络算法

传统的BP神经网络原理包含:向前传输数据,反向传输输出值与样本值间的误差,动态修正权值。在传统的三层BP网络算法中,设输入层、隐含层、输出层分别含有神经元A、B、C个,对应的某一神经单元符号为xi、ym、zn。记xl到ym的权值为Wlm,ym到zn的权值为Wmn,设定传递函数,于是得到网络结构图,见图2。

图2 三层BP网络Fig.2 Three-layer BP network

根据网络顺序,记输入与输出分别为u、v,系统输出的表达式为:

(2)

式中：C为输出结果C的向量。

期望函数为:

D(n)=[d1,d2,…,dC].

(3)

2.2.1工作信号正向传播

输入n个信号,输入层输出:

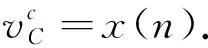
(4)

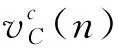
(5)

假设f(·)为sigmoid函数,则网络隐含层的第i个神经元的输出等于:

(6)

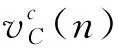
(7)

网络输出层第j个神经元的输出为:

(8)

其相应的误差为

(9)

整个网络的总误差可表示为:

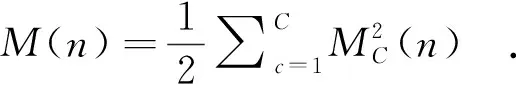
(10)

2.2.2误差信号反向传播

1)调整隐含层与输出层间的连接权值:

=ΔWbc(n)+Wbc(n) .

(11)

此时偏导可表示为:

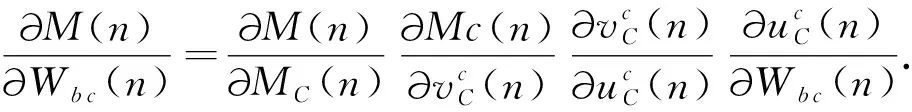
(12)

其中,

再将传递函数用其导数表示,可以得到梯度值如下式:

(13)

再经权值修正量修正后可得到局部梯度如下:

(14)

又因为神经元的局部梯度的传递函数通常是线性的,可知其导数为1。

2)误差信号向前传播,对输入层与隐含层之间的权值Wab进行调整。与上一步类似,应有:

(15)

同样的,有局部梯度为:

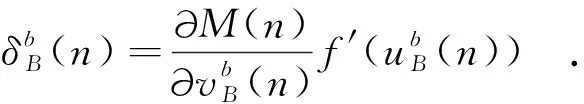
(16)

上式中,f(n)为sigmoid函数。由于隐含层不可见,因此无法直接求出误差对该层输出值的偏导,于是需要上一步计算中求得的输出层节点的局部梯度:

(17)

故有:

(18)

至此,整个神经网络训练过程结束,简言之，修正权值等于系η，局部梯度δ，输出值υ的积，即：可将过程简化表示如下:

ΔW=ηδv.

(19)

3 改进的BP神经网络法

3.1 改进内容

传统的BP神经网络算法中,结果的收敛速度很大程度上取决于常量值学习率,即影响训练时间和训练结果。本文从学习率常数出发,将传统的神经网络学习率常数修改成自适应变化的学习率常数,即记录每次迭代产生的均方误差,及时调整学习率。改进算法为:

(20)

改进算法所对应的权值变化为:

(21)

改进后的神经网络算法可以具体的描述为以下步骤:①选取样本库,设定网络结构,初始化网络权值和阈值,并且设定训练误差允许值ε；②输入样本；③输出结果,计算各层输出误差,再通过训练样本求得样本总体的误差；④调整各层的权值；⑤迭代n+1次,分别向前和反向进行计算,直到误差满足设定的阈值,训练结束。

3.2 改进后神经网络应用

本文从煤矿实际情况出发,建立井下掘进机电压的非线性模型,利用BP神经网络建立配电系统中的电压预测结构。具体分为以下步骤:

1)选择和组织样本数据。选取在区间[-30,30]上的电压,扩大样本容量,并对端口数据进行标准化处理。

2)建立网络结构。建立三层BP网络模型,设定网络节点输入数为10,网络节点输出数为3。根据Hecht-Nielsen理论[7],训练过程中的隐含节点数等于2X+1(X为输入节点数目)。于是,拓扑网络结构就是10×21×3。采集10次数据,将结果作为10维向量输入,输出一个3维向量。

3)系统仿真。设定采样周期为30ms;用二阶惯性系统随机选择数据,并将数据归一化处理;电压标准值设定为220V,波动区间[-30,30];开始训练和测试。具体的测试矢量限于篇幅不再列出,直接给出改进的训练曲线见图3,并将改进后曲线同改进前曲线做对比。

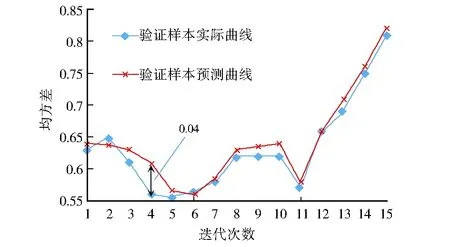
图3 样本曲线对比Fig.3 Comparison of sample curves

通过对比可以看出,预测曲线与实际曲线基本是吻合的,误差最大处为0.04,可以接受。而且发现,传统方法迭代需要234次达到的精度,改进后的迭代算法只需5次就能达到,极大地提升了运算效率。

4 结束语

本文推导了神经网络的算法,阐明了传统BP神经网络在迭代和误差精度上的不足之处。然后通过利用自适应步长法及时调整输入层、隐含层、输出层间的权值,扩大样本容量,归一化样本;将改进的算法用于实践,得到误差较小的预测值。