产业集聚与环境污染关系的再考察——来自中国工业行业的经验证据

(南开大学经济与社会发展研究院与中国科学技术发展战略研究院联合博士后工作站 北京 100038)

1 引言

环境污染近年来已是中国社会最为关注的焦点问题之一。严重的环境污染问题，既与中国仍处于城市化和工业化发展中期、经济发展方式粗放、能源结构以煤为主等因素有关，也与污染防控能力不足等因素有关。值得注意的是，近三十年来与环境不断恶化并行的一大现象是由地方政府出台土地、财税、金融、科技等政策招商引资引致的产业集聚热潮，在全国各地形成了数千家大大小小的工业园区。然而，我们并不能就此得出环境污染是产业集聚导致的结论。研究产业集聚与环境污染之间的关系的文献并不多见，且结论不一。总的说来，研究主要集中于以下三个方面：第一，产业集聚在扩大经济规模的同时往往伴随着工业三废排放的不断增加，这会导致大气污染、水污染、土壤污染，降低农业、旅游业等环境敏感行业的产出，产生明显的环境负外部性[1-3]。第二，产业集聚在促进创新扩散和技术进步、提高企业生产率和竞争力的同时也可能会激励绿色科技的研发应用，通过“创新补偿”效应减弱集聚引发的环境负外部性[4]。第三，在环境规制更为宽松的地区工业污染更加严重，从而产生污染避难所效应，进一步吸引污染密集型工业集聚，但工业集聚在加重环境污染的同时也可能促进环保产业集群的产生和发展[5]，减轻污染避难所效应[6]。近年来，国内部分学者也开始关注产业集聚对环境污染的影响，但研究结论并不一致，经验证据也不够充分。从现实来看，重化工业密集区严重的环境污染似乎表明产业集聚是加剧污染的重要原因，但研究显示，经济活动的空间集聚度提高有利于降低单位工业增加值污染物质排放强度[7]。已公开发表的文献中，李伟娜、杨永福和王珍珍利用制造业行业数据对产业集聚与环境污染的关系进行估计后认为中国的制造业集聚目前处于中级集聚阶段，大气污染问题正在得到缓解[8]。而闫逢柱、苏李和乔娟运用制造业行业数据得出的实证结论则认为产业集聚在短期内有利于降低环境污染，但二者之间在长期并不具有必然的因果关系[9]。李筱乐、原毅军和谢荣辉、杨仁发等基于省级面板数据的研究表明产业集聚与环境污染呈倒U型曲线关系[10-12]。从以上研究看，产业集聚是否具有环境外部性均得到肯定的答案；但环境外部性究竟为正还是负，结论不一。

近十年来，国民绿色发展意识日渐增强，居民的环保呼声成为打造产业园时考虑的重要因素。那么，出于环境保护的角度，应谨慎地发展哪些行业？工业集聚是造成各地环境污染的主要原因吗？我国的工业集聚与环境污染的关系究竟如何？与前述研究多利用静态面板模型不同，本文利用两位数的工业行业动态面板数据对产业集聚与环境污染的动态关系进行实证检验，以回答前述问题。

2 PVAR模型的设定、估计方法与数据描述

2.1 模型设定

本文考察产业集聚与环境污染之间关系的主要方法是建立制造业产业集聚EG指数与环境污染变量的面板数据向量自回归模型PVAR(Panel Data Vector Autoregression)。PVAR模型由Holtz-Eakin、Newey和Rosen正式提出。该方法特别适用于样本数量不够充分的宏观数据分析，并且还综合了面板数据模型和VAR模型的优点，可以同时利用横截面和时间序列的信息，大大增加了观测值的数量和自由度，能控制不可观测的个体异质性，且不需区分内生和外生变量。上述优点使该方法比其他方法更便于考察各变量面对冲击时的动态响应，分析某一变量对其他变量的影响程度。因此，本文设定PVAR模型如下：

zit=αi+βt+Γzit-m+εit

其中：zit是基于面板数据的内生变量环境污染lnpollution和产业集聚lneg所构成的向量；i表示行业；t表示年份；m为滞后期数；Γ是对应的系数矩阵；αi是个体效应向量，作为行业层面的固定效应，体现行业特有的技术含量、资源依赖性等异质性；βt是时间效应向量，可以体现每一时期各行业可能受到的共同冲击。

2.2 估计方法

本文采用的PVAR模型综合了面板分析和VAR模型的优势。因为数据的时间序列较短，所以每个行业的动态特征难以估计。既有的文献分析经常将各横截面结构相同作为一个标准假设，但如果各行业的动态特征差异太大，这一假设会导致外生冲击的短期影响被低估或外生冲击的长期影响被高估。20世纪90年代以来，我国兴起产业集群研究，不少地方政府制定了产业集群规划，有的地方以粗放的方式打造产业集聚区，使得整个制造业行业集聚特征以及环境影响趋同性明显，同时本文采用的模型中加入了控制个体异质性的变量，因此这一假定对本文来说相对合理。值得注意的是，PVAR的模型结构使得固定效应与解释变量相关，因而通常用来消除固定效应的均值差分方法在这个模型中会导致偏误。为避免此类偏误产生，我们使用前向均值差分方法，也即“Helmert变换过程”[13]。这一方法通过消除每个个体每一时期所有未来观测值的均值来保证滞后变量与转换后变量间的正交性。因此，采用PVAR模型时可以使用滞后变量作为工具变量，采用系统广义矩估计(SGMM)方法进行估计。本文采用SGMM方法估计前述PVAR模型参数，并在此基础上利用脉冲响应函数及方差分解方法较好地刻画各种冲击的传导机制，观测各变量面临冲击时的响应情况，分析模型受到冲击时系统所受到的动态影响。

2.3 数据描述与变量说明

样本数据中，环境污染数据均来自历年《中国环境统计年鉴》和《中国环境年鉴》；工业行业数据除2004年选取自国家统计局公布的第一次经济普查数据《中国经济普查年鉴》(2004)以外，其余各年数据均来自历年《中国工业统计年鉴》，所有数据均进行对数变换。为保证统计口径的一致性，工业行业样本首先选取了制造业的20个行业。此外，由于电力、热力的生产和供应业与环境污染和制造业密切相关，数据齐全，故也纳入考察范围。由于相关统计数据的可获得性，本文选取我国除西藏、香港、澳门和台湾外的30个省份1999—2014年21个工业行业的面板数据作为研究对象。

文中采用Ellision和Glaeser提出的EG指数来测定产业集聚程度[14]。因为各行业企业的所有制构成[15]、非正规部门就业人员数的统计误差[16]以及行业间或行业内劳动生产率差异的干扰等原因，若以就业人数作为基础变量会使结果出现较大偏差；所以，为了使不同年份的行业集聚程度可比，以工业总产值变量作为基础变量是较好的选择。但由于国家统计局2011年后不再公布分地区分行业的工业总产值，只公布分地区分行业的工业销售产值，而从历年统计数据看，工业总产值与工业销售产值相近；因此本文用以1990年为不变价格进行换算的工业销售产值作为基础变量。我们以《中国价格统计年鉴》(2015)提供的工业分行业的工业品出厂价格指数(上年=100)为基础构建1999—2011年工业产出的价格平减指数(1990年=100)。其中，由于2002年前的农副食品加工业和普通设备制造业的相关数据缺失，因此分别用食品制造业和专用设备制造业的同期指数替代，最终生成可比的产业集聚指标。Ellision和Glaeser在计算EG指数H时，依据的是详细的企业水平数据，由于中国尚未公开各行业的企业水平数据，我们无法沿用该计算方法。为此，本文假设每个区域的每个行业内的所有企业具有相同规模，即具有相同的工业销售产值，这样就可以通过《中国工业统计年鉴》中的企业单位数和工业销售产值指标对EG指数进行估算。在此假设下的EG指数计算公式为：

式中：k表示产业；i表示区域；nki为区域i拥有产业k的企业数量；Yki为产业k在区域i中的工业销售产值；Yk为产业k的全国工业销售产值；ski=Yki/Yk。由于2011年以后不再公布按地区分组的各行业企业数，只公布各行业的企业数，因此本文以各行业中各地区工业销售产值所占比重与各行业企业数相乘，得出2012年至2014年各地区分行业企业单位数。由此式估算的EG指数虽不可能像Ellision和Glaeser估算的那样精确，但并不妨碍对产业集聚程度的评估与比较[17]。根据调整后的EG指数计算公式，我们计算出中国21个工业行业1999—2014年共16年的产业集聚程度(表1)。从2014年的行业排名来看，前三位行业分别是化学纤维制造业、烟草加工业和黑色金属冶炼及压延加工业。这三个行业均为严重依赖化石能源的行业，因而可以假设在一定时期内这三个行业产业集聚程度的上升可能会导致更高的污染排放。

表1 21个工业行业的EG指数(1999、2014)

环境污染包括大气污染、水污染、土壤污染等多方面。考虑到数据的可获得性，本文衡量环境污染的指标同时囊括了工业废气排放量(二氧化硫排放量、工业烟尘排放量、工业粉尘排放量)、工业废水排放量、工业固体废物产生量等。由于各省区城市化水平和工业化水平处于不同的发展阶段，各种类型环境污染的构成不同，为消除地区间的污染类型差异，集中体现产业集聚水平对环境污染变量变异的解释，本文以各工业行业的单位工业销售产值污染排放量作为环境污染的代理变量。指标值越大，表示环境质量越差，环境污染越严重。其计算方法如下：

lnpollutionit= ln[(indu_SO2it+ soot_dustit+wasterwaterit+solidit)/gvalueit]

式中：pollutionit为t年i产业单位工业销售产值污染排放量；gvalueit为以1990年价格水平计算的t年i产业的工业销售产值；indu_SO2it、soot_dustit、wasterwaterit、solidit分别为工业二氧化硫排放量、工业烟(粉)尘排放量、工业废水排放量、工业固体废物产生量，其中工业烟(粉)尘排放量为工业烟尘排放量和工业粉尘排放量合计数。

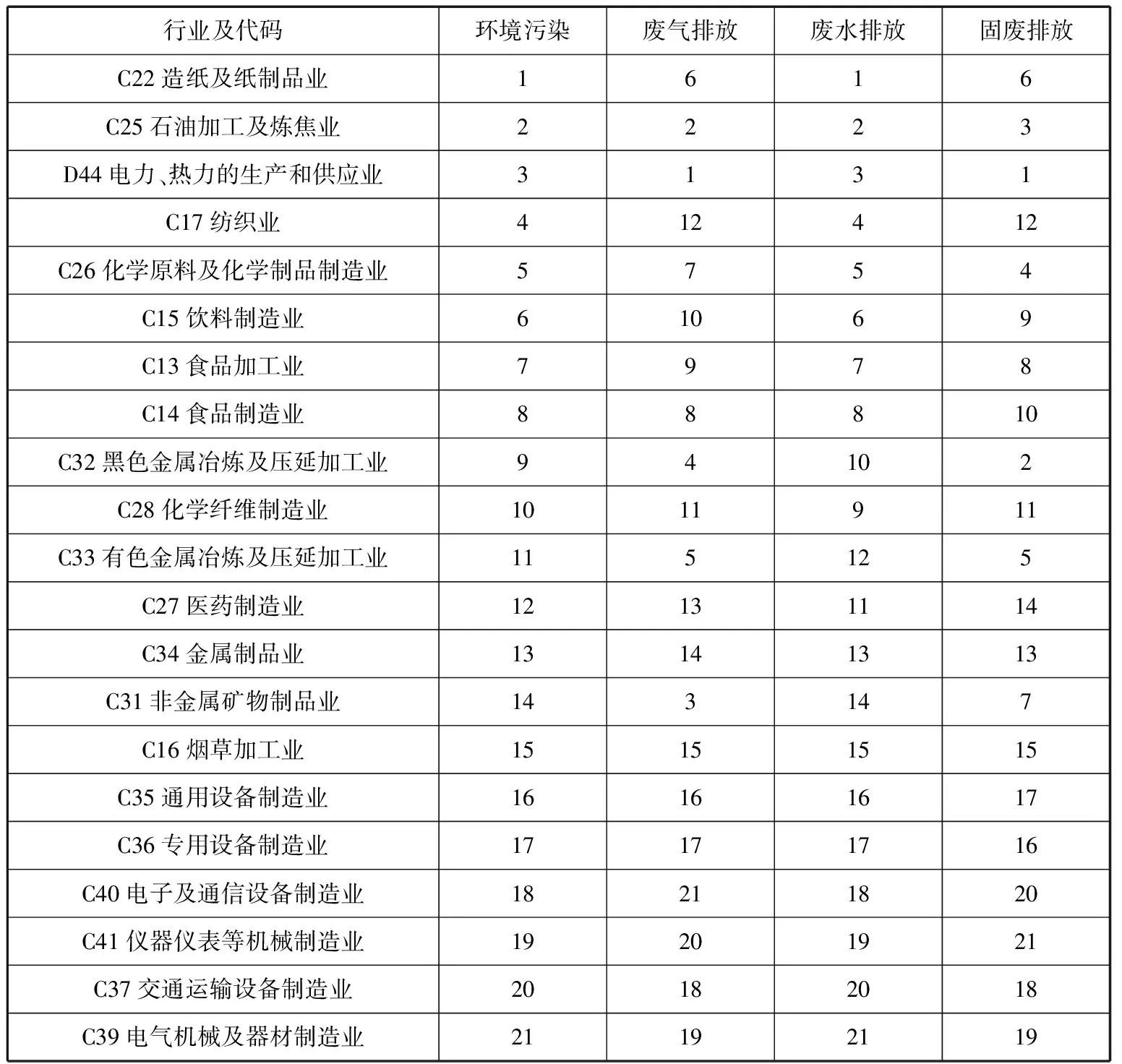
表2 21个工业行业的污染排放强度排名(2014)

3 基于PVAR模型的实证分析

3.1 面板数据的平稳性

为有效避免面板数据模型估计中出现的“伪回归”问题，确保估计结果的有效性，必须对估计所使用的面板数据的平稳性进行检验，最常用的方法是面板单位根检验。为得到稳健的面板单位根检验结论，本文分别采用Breitung检验、IPS检验、HT检验、Fisher-PP、Hadri检验等五种方法进行单位根检验，结果如表3所示。从表中可以看出，前四种检验结果均不能拒绝产业集聚变量lneg和环境污染变量lnpollution的各截面序列在水平值的情形下存在单位根的零假设，Hadri检验拒绝面板数据的不同截面服从平稳过程的零假设，故估计所使用的面板数据为非平稳的。我们对变量的各截面序列进行一阶差分后再进行面板单位根检验，发现相应统计量均在1%显著性水平下显著，整个面板数据服从平稳过程，因此产业集聚变量lneg和环境污染变量lnpollution是同阶单整。若二者之间具有协整关系，则可以建立PVAR模型。

表3 面板数据单位根检验结果

注：1.Hadri检验的零假设是面板数据中的各截面序列均不含有单位根，其余检验的原假设为各截面序列均具有一个单位根。2.检验形式均含常数项和趋势项，HT检验过程中校正了由于样本时期较短导致的水平扭曲，Choi检验运用了Z统计量，即Fisher-PP检验，Hadri检验实施了针对可能存在的异方差的稳健性检验。

3.2 面板协整检验

对于发展中国家或者经济转型中的国家，其宏观经济变量可得的观测值序列往往较短，这会降低传统协整检验的功效，而面板协整检验则可避免这一问题。Westerlund提出两类基于结构而非残差的动态变化的面板协整检验：一类为组均值检验(group-mean test)，统计量为Gt、Ga，备择假设为“至少存在一个协整关系”；另一类为面板检验(panel test)，统计量为Pt、Pa，备择假设为“面板作为一个整体是协整的”。我们利用STATA11.0软件对面板数据集进行协整检验(检验结果见表4)。结果显示产业集聚(lneg)和环境污染(lnpollution)之间存在面板协整关系，即二者之间具有长期稳定的均衡关系。

表4 面板数据协整检验结果

3.3 产业集聚与总环境污染

本文对面板数据进行组间的截面相关检验①、异方差相关检验和面板数据组内相关性检验。结果表明二者不存在截面相关问题，但存在异方差和组内自相关。为稳健起见，我们进一步考虑一阶差分变量dlneg和dlnpollution所构成的二元PVAR系统。如前所述，面板VAR的模型结构可能使得固定效应与解释变量相关，为避免产生偏误，我们首先使用前向均值差分方法进行Helmert变换，然后利用系统广义矩估计法对模型进行估计。表5中列示了滞后3期的PVAR模型估计结果，其中t-1、t-2、t-3分别表示变量滞后一、 二、 三期。②

表5 产业集聚和总环境污染的PVAR估计结果

注：数据部分左侧为GMM估计所得参数，右侧为标准差；***、**、*分别表示1% 、5%、10%的显著性水平。

基于PVAR模型的估计结果，我们利用500次蒙特卡罗模拟得出脉冲响应函数，主要有两大结论。第一，PVAR估计结果表明滞后三期产业集聚对环境污染具有负面影响，但不显著；滞后二期和一期的产业集聚对环境污染具有显著的负面影响，且系数的绝对值越来越大，这意味着随着时间推移，产业集聚会减轻环境污染排放。但脉冲响应函数显示产业集聚程度的升高对环境污染排放的影响并非始终为负。最开始产业集聚在短期内会增加环境污染，但产业集聚程度升高到一定程度后反而会改善环境质量，当产业集聚程度继续升高到某一阈值后又会产生拥挤效应，导致环境又开始恶化。也就是说，产业集聚对环境的影响存在阈值，具有门槛效应。第二，PVAR估计结果表明环境污染随着时间累积对工业集聚存在正向影响，虽然这一结果并不显著，但从脉冲响应图中可以清晰地看到，一单位标准差的环境污染排放冲击在第一期就带来工业集聚的正向波动，在第二期后对工业集聚的影响逐渐减小，最终趋于平稳。因此，估计结果在一定程度上显示中国的工业集聚可能存在“污染避难所”效应。

表6 产业集聚和总环境污染PVAR模型的方差分解

通过方差分解方法可以分析每一个结构冲击对内生变量的方差的贡献度及相对重要性，这样可以粗略地把握变量间的影响，通过脉冲响应函数则可以进一步细致地观察到模型中各变量在受到一次冲击之后的响应过程。由于Choleski正交分解对变量的排序敏感，排列顺序意味着后面变量的同期和滞后期都受前面变量影响，而前面变量只会受后面变量的滞后期的影响。根据经济运行中存在的现实关联关系，变量的排序为产业集聚变量dlneg、环境污染变量dlnpollution。也就是说，由于产业集聚是一个较为缓慢的动态过程，我们假定产业集聚对当期和往期的环境污染产生影响，而产业集聚仅受到往期环境污染变化的影响。从表6中的方差分解结果可以看出：变量的波动在第10期已趋于稳定；产业集聚对环境污染排放变化的贡献率达到2.5%；而环境污染的冲击对产业集聚程度变化的长期解释力大于产业集聚对于环境污染波动的解释力，达4.3%。

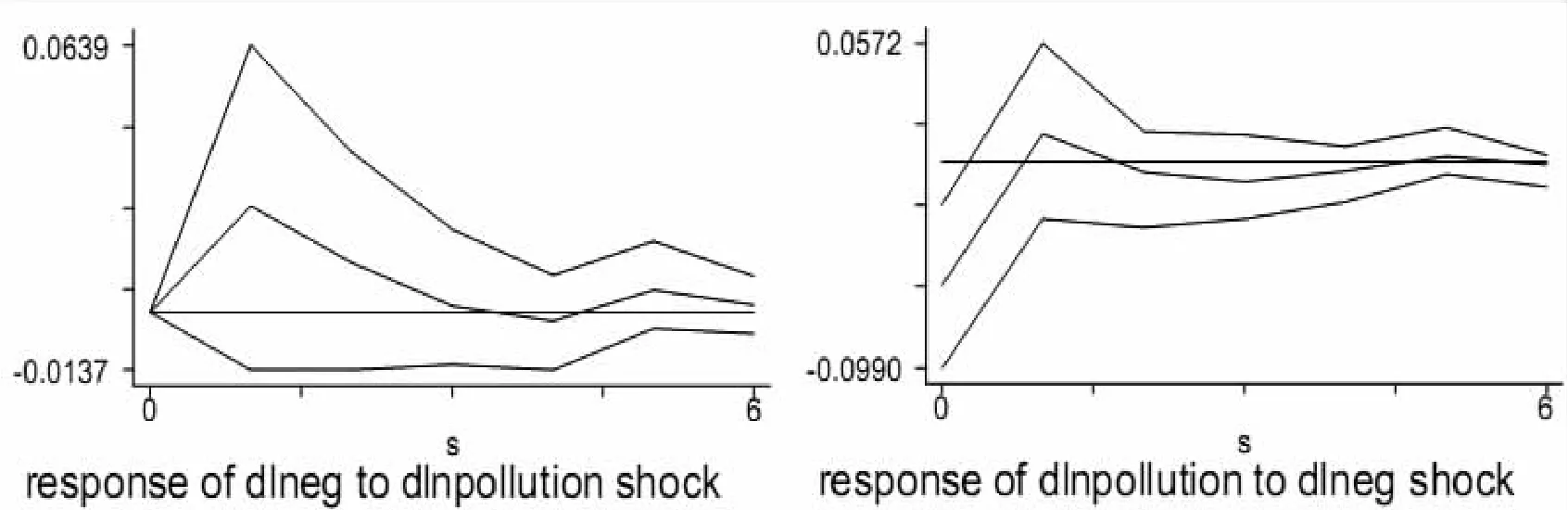
图1 产业集聚和总环境污染的脉冲响应图

3.4 产业集聚和三类环境污染

为细致考察产业集聚与环境污染的关系，同时考虑到工业生产过程中可能带来的废气、废水、废渣排放，我们选取工业废气排放量(包括二氧化硫排放量、工业烟尘排放量、工业粉尘排放量)、工业废水排放量、工业固体废物产生量等三类污染排放作为环境污染的代理变量，并分别取对数后进行一阶差分。面板单位根检验表明一阶差分的序列dlnsolid、dlnwater、dlngas均平稳，可以构建包括dlneg在内的四变量PVAR模型。本文进行滞后3期的PVAR模型估计，并用蒙特卡罗500次模拟得出脉冲响应函数(图2)和方差分解结果(表7)。如前文，由于Choleski 正交分解对变量的排序敏感，根据经济运行中存在的现实关联关系，变量的排序为产业集聚变量dlneg、工业固体废物变量dlnsolid、工业废水变量dlnwater、工业废气变量dlngas。即假定工业产业集聚对当期和往期的工业固体废物产生量、工业废水排放量和工业废气排放量均产生影响，而工业产业集聚自身仅受到往期的三种类型环境污染变化的影响。研究结果如下：

图2 产业集聚和三种环境污染变量的脉冲响应图

第一，在三种工业污染排放中，工业固废对工业集聚程度变化的长期解释力最大，约为5.2%;工业废气排放次之，约为2.9%;工业废水排放的解释力为0.8%。其中，工业固废污染与工业集聚程度的变动方向相反，而工业废气和废水排放与工业集聚的变化方向相同。可能的原因是与工业废气和废水排放相比，工业固废的产生和排放更易观测到，且需占用土地，更易受到环境监管;而废水和废气由于排放更为隐蔽，更易成为“污染避难所”效应的动因。表2显示，工业废水排放前五位的行业包括造纸及纸制品业，石油加工及炼焦业，电力、热力的生产和供应业，纺织业，化学原料及化学制品制造业等行业；工业废气排放前五位的行业包括电力、热力的生产和供应业，石油加工及炼焦业，非金属矿物制品业，黑色金属冶炼及压延加工业，有色金属冶炼及压延加工业等行业。鉴于此，地方政府在招商引资、打造产业集聚区时应考虑造纸及纸制品业等废水、废气排放较高行业的集聚是否是因为本地环境监管过松而来，要对这些行业的企业在行业准入、企业的绿色技术采纳程度等方面加以规制。

第二，工业集聚对工业固废物、废水和废气等三种污染排放变动的贡献率分别达到2.5%、2.3%、0.6%；工业产业集聚的一次正向冲击引起三种污染排放在同期即有较大波动。工业固废和工业废水排放的波动分别于第三期和第二期减弱并趋于稳定，而工业废气排放的波动要到第四期以后才变弱且持续为正，这表明工业集聚的一次正向冲击对工业固废和废水排放具有短期影响，而对工业废气排放具有持久影响。原因可能在于，与废气排放相比，工业固废和废水的排放短期内对人类生产、生活及身体健康的侵害更明显，引发居民异议的可能性更大，受到的环境监管也更为严格；而且与工业固废和废水相比，工业废气排放更为隐蔽，监管难度更大。鉴于此，产业集聚区应特别加强对电力、热力的生产和供应业，石油加工及炼焦业，非金属矿物制品业，黑色金属冶炼及压延加工业，有色金属冶炼及压延加工业等废气排放较高的行业的规制，在产品研发、中试、产业化等全过程加强监管，减弱此类行业对本地环境可能造成的持久影响。

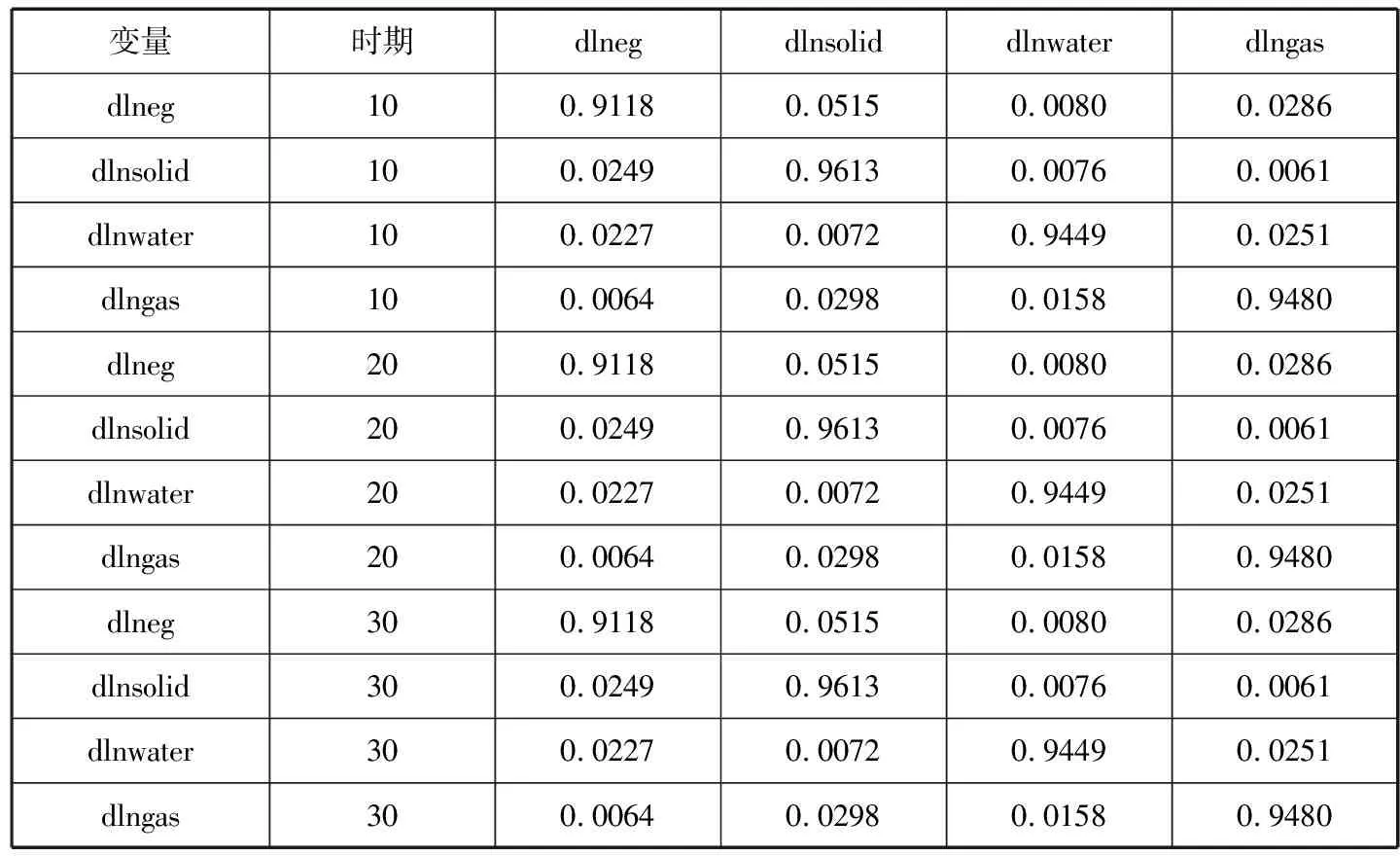
表7 产业集聚和三种环境污染变量PVAR模型的方差分解

4 结论及政策含义

产业集聚会在一定程度上推动地区经济增长，但一个地区经济增长的同时却往往伴随着环境污染的加重，这一点已被大家广泛认同。不过，学者们对二者之间的时空作用机制尚有争议。本文利用工业行业面板数据对产业集聚与环境污染的动态关系进行实证考察，得出如下研究结论：

第一，产业集聚与环境污染之间并非线性关系。产业集聚对环境的影响存在阈值，具有门槛效应，产业集聚对环境污染排放变化的贡献率仅为2.5%。产业集聚在短期内会增加环境污染；从长期看，集聚经济促使效率提高，加之企业出于竞争压力以及环境规制等原因不断进行技术革新，环境污染会逐渐减弱；但当产业集聚程度继续升高达到某一阈值后又会因为拥挤效应而使环境恶化。值得注意的是，本文得出的结论——工业集聚并非环境污染的主因，与很多人的认知不一致。

第二，估计结果显示中国的工业集聚可能存在“污染避难所”效应，且环境污染的冲击对产业集聚程度变化的长期解释力达4.3%，大于产业集聚对于环境污染波动的解释力。出于提高经济总量和财政收入的考虑，有的地方政府有可能在招商引资期间放松环境评价，在产业集聚区的形成期未严格进行环境监管，这样，“污染避难所”效应与产业集聚自我强化的累积循环效应叠加在一起，就可能导致环境规制强度越低的地区工业集聚程度越高。严格的环境规制能够激励企业转型升级，从而极大地促进地区的产业结构调整。既然工业集聚在相当大的程度上得力于地方政府政策的刺激与推动，工业集聚区实际上就成为地方政府决策主导下的一个涉及公共利益的重要产品，那么建设生态工业园区并对其进行评估应该成为地方政府政绩考核体系的重要组成部分。

第三，在影响的持续时间上，工业集聚对工业固体废物的产生和工业废水排放的影响持续时期较短，而对工业废气排放则具有持久影响；在变动方向上，工业集聚程度变动的方向与工业固废污染相反，与工业废气排放相同。与工业废水和工业固体废物相比，工业废气的排放更具隐蔽性，更易成为“污染避难所”效应的动因。鉴于此，地方政府在打造产业集聚区时首先应考虑废气排放较高行业的集聚是否是因本地环境监管过松而来，其次要加强对电力、热力的生产和供应业，石油加工及炼焦业，非金属矿物制品业，黑色金属冶炼及压延加工业，有色金属冶炼及压延加工业等废气排放较高行业的环境规制，要对其产品研发、中试、产业化等全过程实施监管，以减弱此类行业对本地环境可能造成的持久影响。

注释：

① 由于本文数据为“大N小T”型，故采用Peasaran 参数检验和Friedman半参数检验，而非Breusch-Pagan检验。

② 作者感谢世界银行Inessa Love博士对本文Stata程序所提供的帮助。