以形助数直观理解，同类跟进多题归一——从2018年武汉中考数学第24题“网传”解答说起

☉江苏省江阴市璜土中学 戴春萍

各地中考试卷出来之后，很多网站都会第一时间转发试卷及答案，特别是当某份试卷的答案率先传播在网络上，后续的很多网站纷纷转发，而且“原封不动”照搬，有时第一种版本的解答出来之后，随之跟上的转发基本不去纠错、审查，使得错漏一再转发，成为新中考试题转发的一种乱象.网络搜题、检索答案的质量往往不高，与这种不负责任的转发有一定的关联.本文以2018年武汉卷第24题的“网传”解答为例，谈谈我们该怎样研习新中考题，如何开展“有且只有两个点符合要求”问题的解题教学.

一、考题的“网传”解答与“直观”另解

考题1 （2018年湖北武汉中考卷，第24题，有删减）抛物线L：y=-x2+2x+1.如图1，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点.若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标.

“网传”答案：设L1为：y=-x2+2x+t，所以m=t-1且C（0，t），D（2，t），F（1，0），设P（0，a）.

分两种可能的相似对应情形：

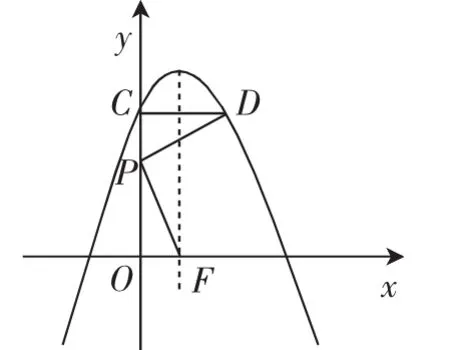
图1

由符合条件的点恰有两个，需要再分两种情况讨论：

情况①：a2-at+2=0有两个相等的实数根.由Δ=0，计算出t=±2，结合t＞0，所以t=2，相应的m1=2-1；

情况②：a2-at+2=0有两个不相等的实数根，且其中一根恰满足t=3a.

Δ＞0，将t=3a代入a2-at+2=0得：a2-3a2+2=0，

解得a=±1，结合a＞0，所以a=1，相应的t=3，m2=2.

将t=3代入a2-at+2=0得：a3=1，对应着P3（0，1）；a4=2，对应着P4（0，2）.

综上所述：当m1=2-1时或P（0，）；当m2=2时，P（0，1）或P（0，2）.

另解展示：由于上述解法从“数”的角度抽象晦涩的运算求解，不利于更多学生的理解，下面我们给出一种更为直观的思考与计算.

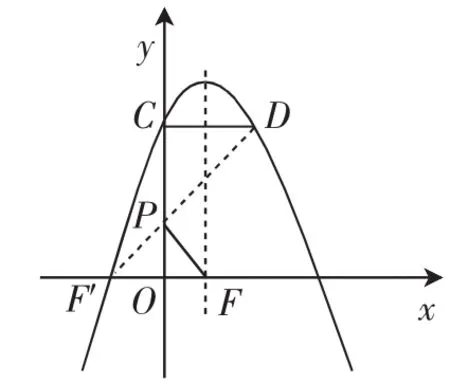
图2

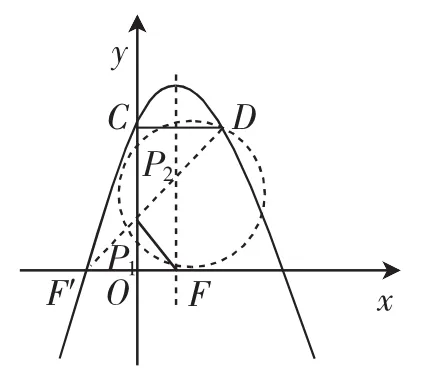
图3

如图2，根据光线平面镜反射性质，取F点关于y轴对称点F′，连接DF′交y轴于P点，则容易确认此时的点P可带来△PCD∽△POF，即不论CD的长度如何变化，这个“光线反射点”总是存在的！此时OF对应着CD，由于它们的数量关系是CD=2OF，所以PC=2OP，此时点P是唯一确定的.

再来想另外一种对应的相似情形，即△PCD∽△FOP，这种情况属于“一线三直角”的基本图形，如图3，本质上就是以DF为直径的圆与y轴的位置关系，当该圆与y轴有公共点时，就存在∠DPF为直角，就满足“一线三直角”.

当该圆与y轴有两个公共点P1，P2时，如图3，点P1，P2都是符合要求的，都能带来△PCD∽△FOP，若再加上之前“光线反射点”，就有三个点满足要求了，当且仅当图3中P1，P2中有一个点恰与“光线反射点”重合，则就是符合题意的恰有两个点符合要求.现在来分析此时点P1的坐标该如何求，可以发现△FF′P是等腰直角三角形，此时P1O=OF=1，相应的CP=2OP=2，OC=3，也就是t=3.进一步可求出此时点P的两个坐标分别是（0，1），（0，2）.

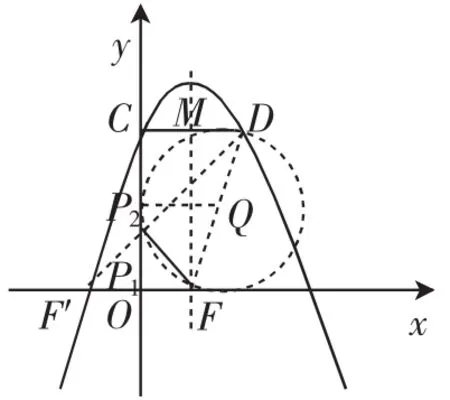
图4

如图4，当以DF为直径的圆（记⊙Q）与y轴只有一个公共点（相切状态）时，连同之前已分析的“光线反射点”，这时也恰有两个点P符合题意.先求得⊙Q的半径QP2为1.5（利用梯形CDFO的中位线可得），于是可把目光投向直角三角形DFM中，直径DF=3，MD=1，FM=t，根据勾股定理可直接读出t=2.相应地就可求出当m=

二、同类链接

考题2 （摘编自南通海门2017年中考模考卷）如图5，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处.若CD边上有且只有2个点G，使△GPD与△GFC相似，请直接写出的值.

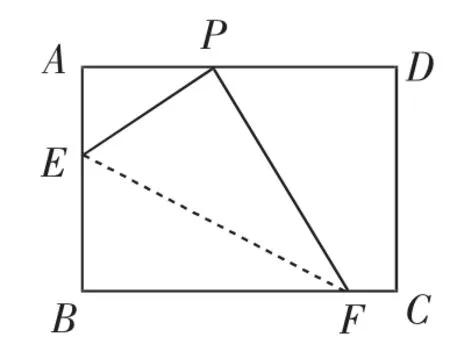
图5

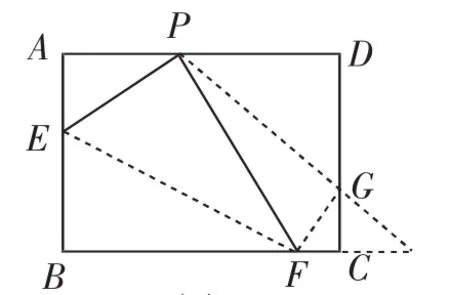
图6

解法简述：如图6，先分析“光线反射点”一定存在，再分析图7中以PF为直径的圆与边CD的公共点情况，类似地，当该圆有两个公共点时，其中一个公共点需要与前面图6中的G点重合在一起.

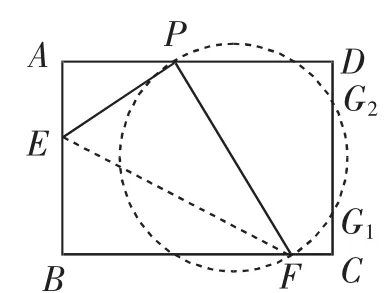
图7

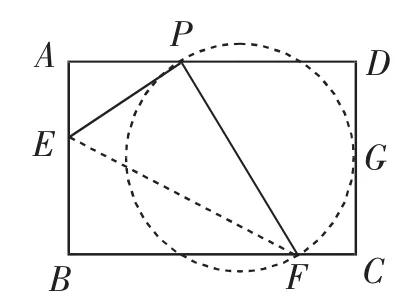
图8

还有一种情况，就是以PF为直径的圆与CD恰有一个公共点（相切）时（如图8），连同前面“光线反射点”一起也符合题意“恰有两个点G”.在这两种情况下可分别求出的值为或

三、教学思考

1.引导学生准备解读关键词“恰有”“有且只有”

在初中数学语言中“有且只有”比较独特，既指出存在性，又指出唯一性.学生在初学几何时有“经过两点有且只有一条直线”“过一点有且只有一条直线与已知直线垂直”等等，学生并不陌生.但是到了中考训练时常常出现一类“恰有两点”“有且只有两点”的问题，学生在几何模型中难以找到直接转化的方向，思路受阻.这时在解题教学的过程中就需要引导学生解读“恰有一点”“有且只有一点”的几何模型，学生就能想到圆与直线的位置关系中的相切，以及“光线反射点”等几何模型，把思路迁移到问题中来，尝试打开思路.

2.设计铺垫式问题，直观构图有效破解问题难点

讲评“考题1”时，如果像“网传”解答一样照本宣科，估计会的学生懂，不会的学生仍然是不知所云.因为“数”的解法的抽象晦涩需要有“形”的直观解释.这就是我们在后面给的直观揭示，通过分解图形，各个击破，试图从“形”的直观角度来给出解释，让学生感受“恰有两点”存在，这两点恰在什么位置？让学生看得见、算得出，当然，直观构图的方法也使得运算量大为简化.如果说数形结合有三个角度：以形助数、以数驭形、数形互助，那么我们给出的分解图形、铺垫问题难点的方法也就应该属于“以形助数”了.

3.善于同类跟进，“多题归一”感悟问题结构

讲一些具有独特结构或关键词的习题时，如果只有一例讲评或订正之后，如果隔一两天再安排检测，则效果往往不好，原因就是学生在一例练习或讲评之后印象并不深刻.这时有效的方式是讲评一例之后即时开展同类跟进，让学生在“多题归一”中巩固、内化问题结构，达到深刻理解的程度.这也是上文中再给出一个考题2的用意所在.当然，这就要求老师在平时的解题研究中要善于开展同类搜集与归类存档，这样到了讲评某道习题时，就能“信手”找到，而不是习惯到网上搜题（目前网络提供关键词或拍图检索比较方便），但是对于问题深层结构的相似，还是需要教师自己花时间积累和整理的.