前交叉韧带断裂三维不对称度步态分析初探

李玳，于宏，梁子轩，黄红拾，石海华，刘晓民，敖英芳

1.北京大学第三医院运动医学研究所，北京市运动医学关节伤病重点实验室，北京市100191；2.北京工业大学信息学部信息与通信工程学院，北京市100124

目的 步态分析对于下肢损伤部位及程度描述具有重要作用，而对称度是步态特征的重要指标。本研究将在三维空间定量描述步态信息及其不对称度，深入挖掘步态信息，完善疾病异常步态特征分析。

方法 基于惯性步态传感器获得不同部位的冠状面-矢状面角度变化信息，反向重建步态空间矢量，构建运动曲线，形成基于三维空间角度矢量距离的运动对称性检测方法。于2017年7月至2018年1月对健康人(正常组)和单纯前交叉韧带(ACL)断裂患者(ACL组)进行特征分析，验证其效果。

结果 小腿、大腿和膝关节不对称度D方面两组有较好的区分效果(P＜0.05)。其中小腿空间运动矢量特征对组间辨识度较高且区分相对稳定，与性别、年龄、身高、体质量指数无关。

结论 通过两侧惯性传感器获得左右肢体时间-冠状面-矢状面空间曲线图，在三维空间中计算相应周期所有时间点的欧式空间距离平方的平均值，可作为步态不对称度分析方法。

下肢各关节损伤在运动损伤中最为常见，对运动损伤的准确评估是进行康复治疗的前提。步态分析是下肢运动评估的基础，也是近年来的研究热点。

步态特征是进行步态分析的核心[1-9]。当前步态特征主要有时空步态描述、频域步态描述和足底力学三大类，测量方法主要如下。①基于空间标记点的步态描述：在被测者身体目标位置固定反光标记点，通过分布于检测空间中的数个相机，组成立体视觉测量系统，获得每个标记点的空间坐标，根据每个标记点与肢体坐标系之间的变换关系，计算目标肢体夹角。②惯性元件测量法：在被测者肢体特定部位捆绑惯性元件，主要为加速度传感器或陀螺仪[10-11]，通过计算运动时惯性元件输出各个方向的加速度信息，通过时间积分，获得角速度信息，再次积分可获得角度信息[12]。③足底压力测量：在固定路线上铺设压力传感器阵列，被测者在压力传感器阵列上自然步行通过，测量压力分布随时间变化数据，主要有足底压力分布、足底压力对称性、重心偏移度等参数[13-21]。④其他还有超声法、磁偏角法等方法进行步态分析[22]。

上述大多数时空步态特征既要关注健患侧各自的变化，还要对比分析两侧之间的特征值差异。因此，对称度是评价步态的重要指标。现有对称度指标大多为二维平面夹角的差值、比值和差比值，且多为对关节夹角的单纯分析，无空间轨迹分析对比下肢运动产生的三维空间角度[23-25]。因此，本研究提出基于下肢空间角度综合评价的运动对称性检测方法和指标，构建运动曲线，以期获得更接近真实运动的特征指标。

1 资料与方法

1.1 一般资料

2017年7月至2018年1月招募正常受试者(北京大学第三医院医务工作者、全国各地进修医生、研究生和实习生)为正常组。选择在北京大学第三医院运动医学研究所拟行前交叉韧带(anterior cruciate ligament,ACL)重建术的术前患者为ACL组。

纳入标准：正常组既往无腰部以下手术及重大外伤史，近期无损伤疼痛功能障碍；ACL组均为单侧损伤，单纯ACL断裂且不并发其他韧带损伤，后期经关节镜证实，能独立步行10 m以上。

正常组66例，年龄18～63岁，身高150.0～187.0 cm，体质量指数(body mass index,BMI)17.19～33.61 kg/m2。

ACL组64例，年龄15～58岁，身高156.0～192.0 cm，BMI 17.30～35.49 kg/m2。

采用GaitSmart(ETB,European Technology for Business Ltd.，英国)惯性测量系统，在被测者左右两侧骨盆、左右大腿中间位置外侧、小腿中间位置外侧各布置一个惯性传感器(见图1)。记录每个传感器测量的角度随被测者步行时的变化数值。

所有受试者穿平底鞋，静止站立10 s以获得传感器同步；自选舒适速度独立行走10 m以上，自由摆臂，折返1～2次。

本课题获北京大学第三医院伦理委员会审核批准(批号：M2017157)。

图1 步态惯性测量法

1.2 不对称度D构建方法

根据GaitSmart 6个传感器获得的左右骨盆、大腿、小腿与冠状面和矢状面的夹角信息，重建肢体三维偏转角。

如图2所示，设三维空间世界坐标系OXYZ，肢体(如大腿)上有一空间点A，由于惯性器件不能保证始终垂直于地面，故设过A点有一自由直线AB为惯性元件的中心轴线，与Y轴空间夹角为θ，当被测者步行时，大腿发生空间摆动，直线AB在OXYZ坐标内发生自由旋转，此时与Y轴空间夹角为(θ+Δθ)，设(θ+Δθ)向XOY平面投影时，即为直线AB空间倾角在冠状面的倾角，向YOZ平面投影时，即为直线AB空间倾角与矢状面的夹角。反之，如果有AB与冠状面和矢状面的夹角时，联合时间轴，即可获得一种空间三维结构，但与OXYZ坐标系有所不同，为时间-冠状面-矢状面三维偏角坐标系，设为oαβt坐标系。被测者步行时，左右腿在oαβt坐标系中分别形成两条空间曲线L1和L2。计算每个时间点L1(i)与L2(i+Δi)之间的欧式空间距离，Δi为左右侧时间上的相位差，然后将这些空间距离平方求和再取平均，即得到左右两侧运动的不对称性。为了使不同的步行时间具有可比性，将L1(i)与L2(i+Δi)之间的欧式空间距离平方和除以总点数，得到平均偏差度作为最后的左右运动不对称性。

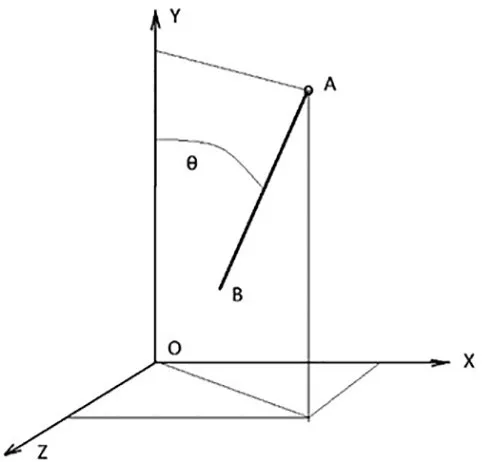
图2 空间直线投影示意图

定义平均不对称度D：

其中n为选取的平稳周期中点的个数，每点时间间隔约为0.01 s，即每隔1 ms记录相应部位左右侧与矢状面和冠状面夹角，Δi为左右侧时间上的相位差。L1为左侧肢体与矢状面夹角和与冠状面夹角组成的数据集，L2为右侧肢体与矢状面夹角和与冠状面夹角组成的数据集。若两侧完全对称，D值为0。

1.3 人群验证

根据式(1)方法计算小腿、大腿、骨盆、膝关节和髋关节偏转角的平均不对称度D，分析比较正常组与ACL组的不对称度D及其与年龄、性别、身高和BMI的关系，选取能有效区分两类患者的不对称度特征。

1.4 统计学分析

应用SPSS 18.0进行数据统计分析。所有数据均进行Kolmogorov-Smirnov正态性检验。符合正态连续变量，用(xˉ±s)表示；非正态分布变量采用M(Q25,Q75)表示。检验数据线性、独立、残差正态、方差齐性、杠杆点及强影响点、多重共线性结果。应用多重线性回归进行组间及性别、年龄、身高和BMI的相关性分析，列出对应决定系数r2值、偏回归系数B及相应显著性检验P值。

2 结果

2.1 不对称度D的计算

对正常组左侧数据进行计算，得到正常组左侧小腿、大腿、骨盆、膝关节和髋关节夹角变化幅度。见表1。

由结果可见，相比于其他部位的角度变化幅度，正常组小腿角度变化幅度最大，且小腿角度变化曲线平滑度、分辨度高(见图3a)。除了骨盆，相比于与冠状面夹角，与矢状面夹角变化幅度明显要大很多，获得数据时信噪比大，正确辨识度高(见图3b)。

ACL组按同样方法进行计算，得到相同结果。故以小腿与矢状面的夹角信息为标准获取健康人与ACL断裂患者的稳定周期中的一个周期、左右相位差和起始点的值。具体选取周期、确定相位方法是在左侧小腿与矢状面夹角的时间-角度图中选取稳定周期中的一个完整周期，即用局部最值(extremum)的两点作为起点和终点，确定周期的大小，在右侧寻找对应的起点与左侧起点差值，确定时间上的相位差。

图3为某被测健康人的小腿、大腿、骨盆、膝关节和髋关节与矢状面、冠状面的夹角以及左右肢体时间-冠状面-矢状面空间曲线图。

表1 正常组左侧小腿、大腿、骨盆、膝关节和髋关节夹角变化幅度(°)

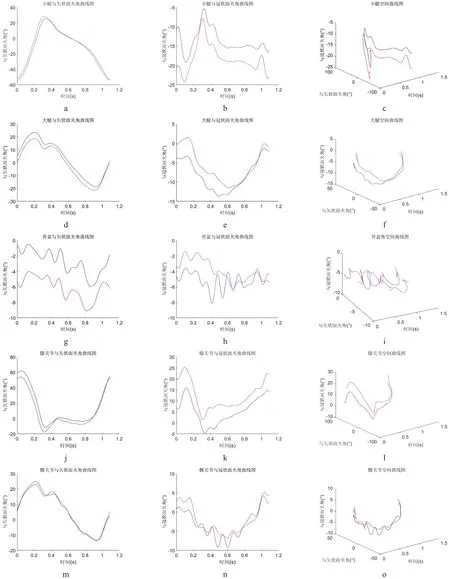
图3 下肢不同部位与矢状面、冠状面夹角以及左右肢体的时间-冠状面-矢状面空间曲线图

根据得到的周期、左右相位差和起始点的值以及式(1)，计算获得样本的平均不对称度D值：小腿偏转角为36，大腿偏转角为22，骨盆偏转角为16，膝关节偏转角为93，髋关节偏转角为5。

2.2 不对称度D的比较

根据2.1中步骤及式(1)计算得到每位受试者的小腿、大腿角、骨盆、膝关节和髋关节偏转角的平均不对称度D。两组数据正态性检验结果见表2。

小腿、大腿和膝关节不对称度方面两组有较好的区分效果(P＜0.05)。其中小腿空间运动矢量特征对组间辨识度较高且区分相对稳定(P＜0.001)，与性别、年龄、身高和BMI无关(P＞0.05)。见表3。

3 讨论

本研究基于佩戴在被测者身体上的惯性步态传感器获得不同部位与冠状面和矢状面夹角变化信息，反向重建步态空间矢量特征，首次在三维空间定量描述步态信息，重点描述左右腿的运动不对称度。

本研究原始数据为正常人与ACL断裂患者在一定区域内做折返行走运动，惯性元件测量仪器测得两侧小腿、大腿、骨盆、膝关节和髋关节与矢状面和冠状面的夹角[12]。由于个体的差异，不能对被测者进行统一的周期和相位划分，要根据个体步速和步幅进行调整，所以需要针对每个人取各自对应的周期相位。获取正常人与ACL断裂患者的稳定周期、左右相位差和起始点的值，为平均不对称度的计算做准备[23]。

本研究通过每个惯性传感器获得左右肢体时间-冠状面-矢状面空间曲线图，在三维空间中计算所有时间点的欧式空间距离平方的平均值作为步态不对称度分析方法。若直接采用三维空间欧氏距离，最后得到的结果在显示上不明显。另外，若直接L1与L2相减，得到的对称度存在正负抵消的情况，容易出现错误的结果。所以采用欧式距离的平方作为直观的判断依据，也不会影响最后结果的分析。

本研究还可以带入不同时间值计算步态周期关键点时刻的不对称度。如摆动期最大屈膝角度时刻、支撑期最小屈膝角度时刻等一些有临床意义的指标[24-25]。

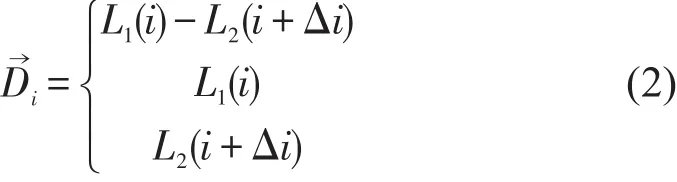
其中，D→i表征步态周期关键时间点的计算，i为任意时间点，Δi为左右侧时间上的相位差。

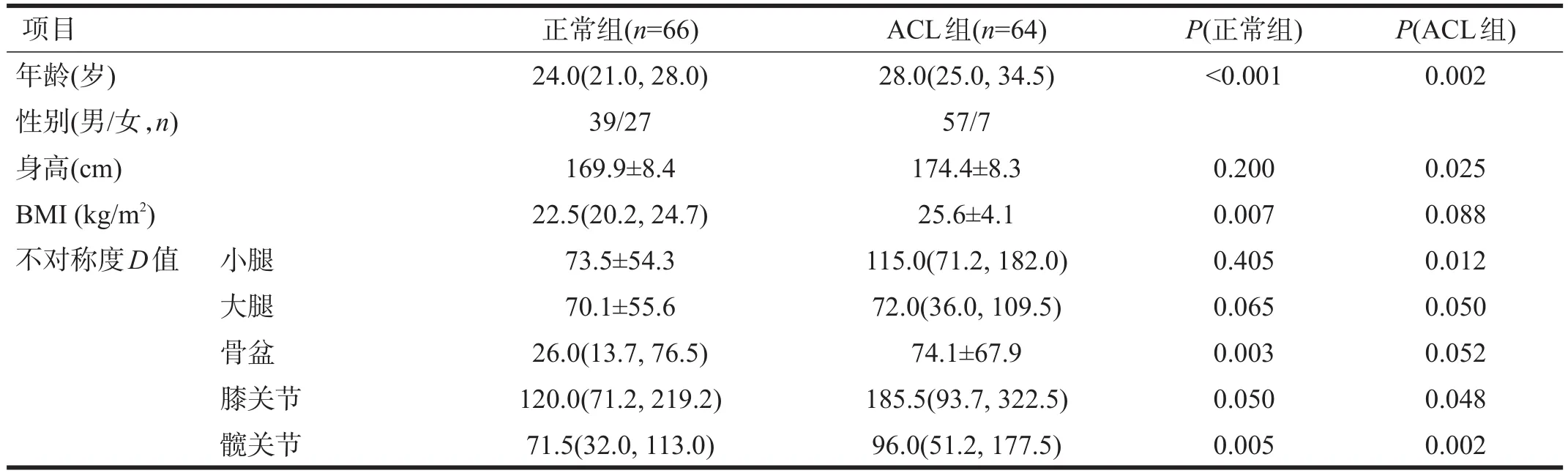
表2 正常组和ACL组的正态性检验

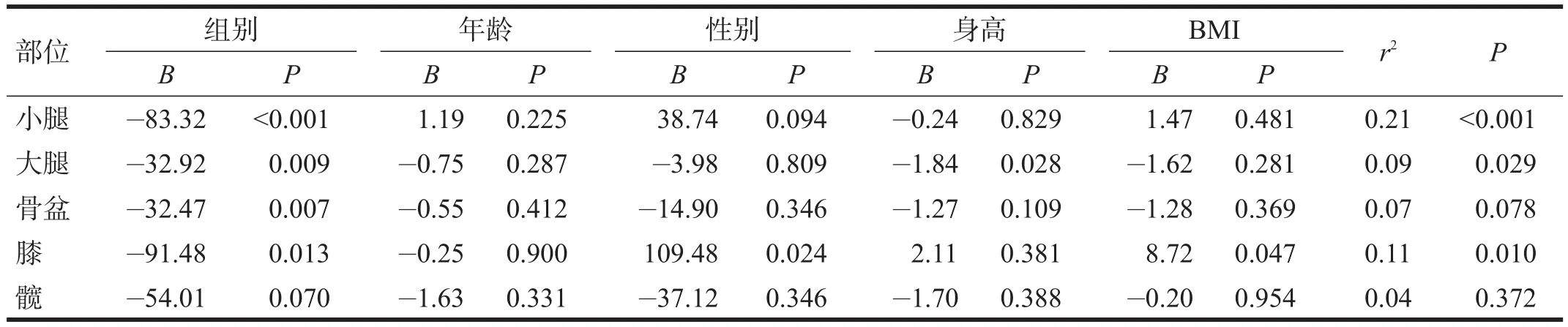
表3 两组多重线性回归系数和模型拟合度

目前光学定位精度较高，可达到0.1 mm。而且因为获得的是贴于肢体骨性点的多个标记点坐标，所以，该方法获得的信息量大，直观，参数易于理解，是步态特征识别中的重要方法。但该方法需要人工粘贴标记点或标记球，粘贴误差较大。当被贴部位皮肤松弛或皮下脂肪较多时，标记点在运动情况下不稳定，造成数据震荡严重，影响步态识别精度。该方法通常需要较大的测量环境，相机数量多，成本高，且对光场环境敏感，一般用于专业实验室中，限制了该方法的应用。

本研究采取的惯性元件测量仅需在被测者特定位置捆绑惯性元件[12]，具有涉及个人隐私程度低、使用方便、不受空间和线路限制、造价低等优点。本研究方法亦可用于左右躯体上任意对应传感器数据对的对称性计算[10-11]。结合本研究多重回归分析结果可以看出，小腿、大腿和膝关节组间差异有统计学意义，其中小腿差异最显著。小腿空间运动矢量特征对组间辨识度较高，区分相对稳定，与性别、年龄、身高和BMI均无关，可以得出，小腿偏转角不对称度是识别正常组和ACL断裂患者较为理想的特征指标。如在某些情景需要减少传感器数量使用时，可选择单纯小腿佩戴，操作更加简便，降低成本，便于应用。不足之处是，该方法由于采用积分法测量空间角度，容易形成时间累积误差，测量精度略低。因此，还需要进一步优化算法，提高精确度，以便更好地推广。

本研究构建的空间矢量指标也是一种新颖的尝试，因同时结合矢状面和冠状面信息，较传统单一平面夹角指标的区分度更大，并可通过各空间曲线整体观察哪些时间点和部位的差异最大，继而取该时间点的力学信息进行计算，进一步分析原因，为临床分析起到有效的指导作用。

空间运动特征分析更接近于实际肢体使用状态，为此，本研究将时间轴、与冠状面夹角、与矢状面夹角形成时间-冠状面-矢状面空间曲线，分别获得左右肢体的该矢量特征。在三维空间中计算所有时间点的欧式空间距离平方的平均值，可作为步态不对称度分析方法。小腿空间运动矢量特征对于正常人和ACL断裂患者之间的辨识度较高且相对稳定。