EKF与互补融合滤波在姿态解算中的研究*
王 见,马建林
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.重庆大学机械工程学院,重庆 400044)
如今姿态测量已经成为一个重要的研究领域,随着现代微机电系统MEMS(Micro Electro Mechanical System)技术的发展,在姿态测量场合应用低成本的捷联惯性测量单元IMU(Inertial Measurement Unit)来对姿态进行精确实时测量变得非常普遍。
IMU是以陀螺仪和加速度计等敏感器件组成的导航姿态解算系统,此系统根据加速度计和陀螺仪输出的加速度、角速度等信息解算出载体的角度、速度和位移等参数量[1]。该系统广泛应用于导航、飞控等各种测量领域,由于其加速度和陀螺仪的输出数据受到温度、工作电磁环境、运行时间等各种因素的影响,输出的数据常常带有偏差。通过广大学者对姿态解算方法策略的研究,目前主要的研究方法为:欧拉法、方向余弦法与四元数法。由于欧拉角法不能用于全姿态解算,方向余弦法方程的计算量大,工作效率低,而四元数法能避免上述问题,因此四元数法的研究得到了广泛重视[2]。
对于多数滤波算法由于其本身的局限性,并不能很好的融合多类型传感器测量信息,或者解算中失去过往信号的特征信息。由于互补滤波能较好的融合加速度和陀螺仪数据,滤除信号中加速度计的高频噪声和陀螺仪的低频噪声,结合四元数法,能全姿解算姿态数据,因此广泛用于IMU滤波中。而EKF则能较好解决非线性系统滤波问题,且本身是一种基于状态方程的滤波策略,并通过卡尔曼增益算子将当前测量数据和过去状态关联起来,便可得到更为可靠的矫正数据。本文通过对互补滤波和EKF的融合,提出EKF与互补滤波融合算法,兼顾了多传感器信息融合和关联过往测量信息的解算特性,得到更接近真实状态下的解算数据,为其他研究应用提供了参考。
1 捷联惯性导航系统姿态解算
姿态测量过程中,往往载体的姿态方位等参数信息变化速率较大,这样就对姿态矩阵的实时计算提出了更高的要求[3]。在惯性导航系统中,将惯性敏感器件输出的角速度、速度、角加速度等参数量信息经过除噪等滤波处理后,再配合误差补偿、积分等操作来得到位置、姿态等相关有用信息。表示姿态时,则用载体坐标系相对导航坐标系的3个轴转动角度确定,习惯上按照航空航天领域规定XYZ为欧拉角的旋转顺序,滚转角γ为绕X旋转,俯仰角θ表绕Y轴旋转,偏航角ψ表绕Z旋转。
目前主要的研究方法为:欧拉角法、方向余弦法与四元数法。而根据各个方法的优劣特点,常常选用四元数法的居多。

图1 捷联式惯性导航原理图
四元数是用一个四维的向量来表示三维空间的旋转,当绕一个旋转轴ϖ旋转一个角度θ′,用q可表示其旋转,由于四元数在求解4个未知量的线性微分方程组时,计算量小,易于操作,是比较实用的工程方法[4]。
(1)
式中:实部q0表示的是转角一半的余弦值,虚部q1~q3中转角一半正弦值的系数rx、ry、rz分别表示瞬时转动轴与参考坐标系间的方向余弦值。
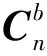
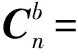
(2)
(3)
对照旋转矩阵的欧拉角表示,可以解出用四元数表示的欧拉角:
(4)
2 互补滤波理论
在多传感器数据融合过程中进行误差修正是非常必要的[6]。互补滤波器从频域的角度来分辨噪声[7]。由于加速度、陀螺仪以及电力罗盘/磁力计的工作原理特性决定了这些惯性测量器件本身存在一些不可避免的缺陷。其中,加速度计和电子罗盘动态响应特性较差,但测量过程中不会存在累积误差,而陀螺仪动态响应特性良好,角速度瞬时精度高,但测量使用过程中由于漂移和积分运算,计算出的姿态角会产生累积误差[5]。这样使得他们在频域上的特性形成互补,因此采用互补滤波算法融合这3种传感器的数据,可以有效提高测量精度和系统的动态性能[8]。
(5)
因此,通过互补滤波器的滤波处理,滤除加速度、磁力计的高频噪声和陀螺仪的低频噪声,得到3个方向的修正误差,结合kp、ki系数计算出累积误差,在此,、系数选取独立互补滤波常用的经验数据,为2.0控制误差反馈速度,ki取0.01用来控制误差积分速度,最后利用修正后的陀螺仪角速度数据结合一阶龙格—库塔法(Runge-Kutta methods)更新四元数微分方程,
q0=q0+(-q1gx-q2gy-q3gz)T
q1=q1+(q0gx+q2gz-q3gy)T
q2=q2+(q0gy-q1gz+q3gx)T
q3=q3+(q0gz+q1gy-q2gx)T
(6)
式中:gx、gy、gz表示陀螺仪x、y、z轴的角速度,T表示采样周期,通过此种用加速度修正陀螺仪偏差的互补方法,便能够很好的融合三者采集的数据,得到最接近实际的解算值。
在对互补滤波解算得出的四元数进行下一状态更新过程中,需得建立四元数更新状态方程,四元数是由姿态矩阵推算得来的,参照姿态矩阵微分方程,得到四元数微分方程如下:
(7)
记[ω×]如下:
(8)
则对于四元数更新方程有:
(9)
由于该种状态更新方法是一个求积分的做法,在实际中不可避免的会出现误差发散,长时间之后这个办法给出的姿态不具有太高的可信度了,因此在应用中还需要注意一个问题,由于角度测量的误差,四元数/姿态矩阵在一段时间后可能会不满足归一性/正交性,每次更新四元数需要对其矩阵做归一化/正交化处理,最后用归一化后的四元数解算当前时刻的欧拉角数据。互补滤波结构框图如图2所示。

图2 互补滤波结构模型
3 扩展卡尔曼滤波(EKF)算法
最初提出的卡尔曼滤波基本理论只适用于状态方程和量测方程均为线性的随机线性高斯系统。但是实际中大部分系统是非线性的,其中还有许多是强非线性的。解决函数非线性问题的最直接思路是对非线性函数线性化,EKF是基于该思路的最为实用的非线性滤波算法[9]。扩展卡尔曼滤波(Extended kalman filter,EKF)其基本思想是将非线性状态函数和量测函数进行局部线性化,即进行一阶Taylor多项式展开,然后应用线性系统Kalman滤波算法来处理[10]。
定义系统状态变量为Xk∈Rn,系统过程激励噪声为wk,测量矩阵Zk∈Rm,观测噪声为vk,可得出系统的状态和量测方程为[11]:
(10)
式中:φk/k-1为测量状态方程矩阵,H为观测向量控制矩阵,Q、R分别为过程激励噪声协方差矩阵和观测噪声协方差矩阵[12]。
卡尔曼滤波(KF),是一种基于统计学理论的线性模型滤波算法,是综合运用上一状态的统计学误差和此刻测量值的误差来估计当前状态的最优值,而上一状态最优值和当前测量值各自占比又是通过卡尔曼增益来即时变化调整的,是一种在线处理方式[13]。当前对于KF的改进有多种方法,主要研究热点集中在针对系统模型非线性或系统噪声统计特性不明确引起的滤波器精度降低甚至发散这一问题的改进上[14]。在运用卡尔曼模型时,可以分成5个主要步骤,分别对应5个重要的公式模型[15]:
①状态预测方程:
(11)
②协方差预测方程:
(12)
③卡尔曼增益计算:
Kg=Pk|k-1HT/(HPk|k-1HT+R)
(13)
④方差更新方程:
(14)
⑤协方差更新过程:
Pk=(1-KgH)Pk|k-1
(15)
根据欧拉角的一阶离散更新方程,结合欧拉角矩阵微分方程[2],建立卡尔曼滤波状态方程为:
(16)
EKF(扩展卡尔曼滤波)通过对状态函数的非线性部分在上一状态时刻进行Taylor级数展开,取其一阶偏导部分,忽略高阶项,从而得到系统的近似线性状态模型,以利用KF算法进行滤波估计。本系统中,欧拉角状态方程非线性部分f(Xk-1)经线性化处理后所得的雅可比矩阵(jacobi matrix)加上上一状态欧拉角和噪声矩阵后,状态方程为Xk=φk/k-1Xk-1+wk,其中φk/k-1为:
(17)

图3 实验设备图
4 实验结果和分析
为了检验算法理论的适用性,借助由6轴MEMS惯性测量单元MPU6500和MEMS三轴磁力计AK8963组合而成的可提供共9轴速度和温度信息的导航传感器MPU9250来进行算法验证。传感器置于3D打印的安装台上,安装台与高精度步进电机输出轴连接,通过调节步进电机的拨码开关将步进电机转轴的步进角调为最小(1.8/16=0.11°),确保电机转动角度足够精确,控制步进电机向两个方向分别转动20°,传感器在步进电机的旋转过程中采集数据。STM32处理器将采集到的MPU9250传感器的原始数据保存在SD卡的文件中,文件拷贝到电脑上,后借助MATLAB软件读取采集的原始数据,按照互补滤波和扩展卡尔曼滤波EKF的滤波理论进行编程验证滤波效果。
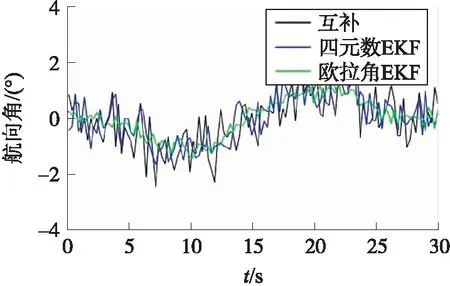
图5 俯仰角θ滤波结果
实验分两部分,首先在静止状态下采集数据,得到零漂数据大小。然后控制步进电机来回转动20°,将采集到的动态数据减去零漂数据后进行后续算法处理。下面分别给出了用3种不同方法对采集的数据进行偏航角ψ、横滚角γ、俯仰角θ解算的效果图。
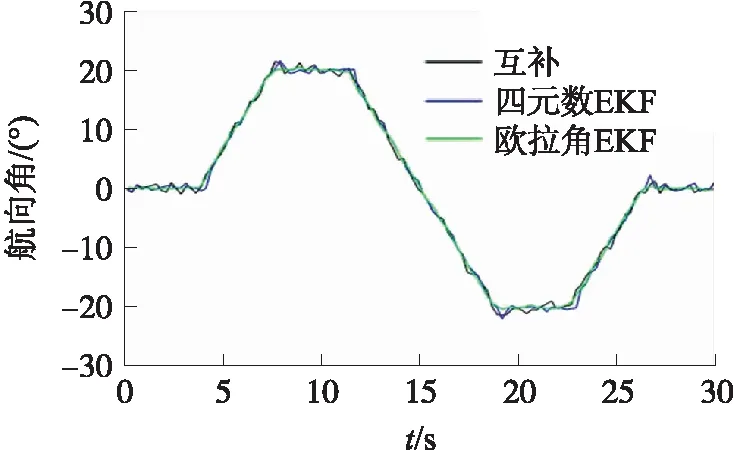
图4 偏航角ψ滤波结果
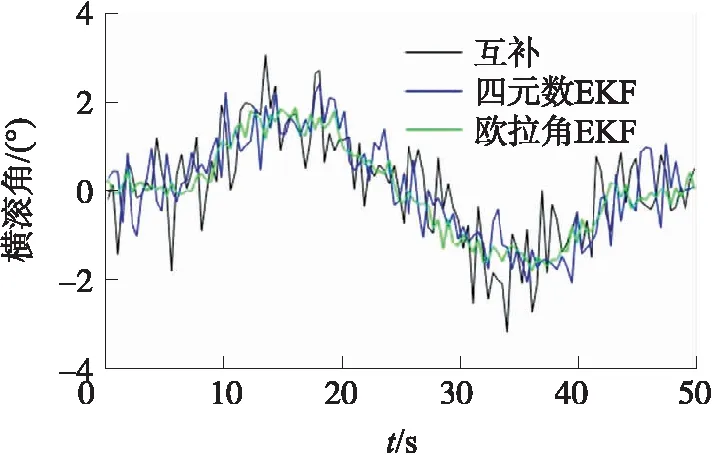
图6 横滚角γ滤波结果
由于步进电机竖直固定放置,电机轴旋转带来的主要为航向角ψ的变化,对于横滚角γ和俯仰角θ变化量极少。主要从航向角的滤波解算结果看出,对互补四元数进行EKF滤波后的结果虽比互补滤波的结果波动频率减小、噪声误差也得到一定减小,但都存在一定的超调量。而对互补滤波的欧拉角结果进行EKF矫正处理则不但使解算结果的随机误差、解算结果波动明显减少,也不存在解算超调量的问题,姿态解算结果曲线更加平滑,能更真实地反应姿态变化情况。
同时,通过统计偏航角ψ在稳态8 s至10.5 s时间段下的的方差值、波动值可以得出:
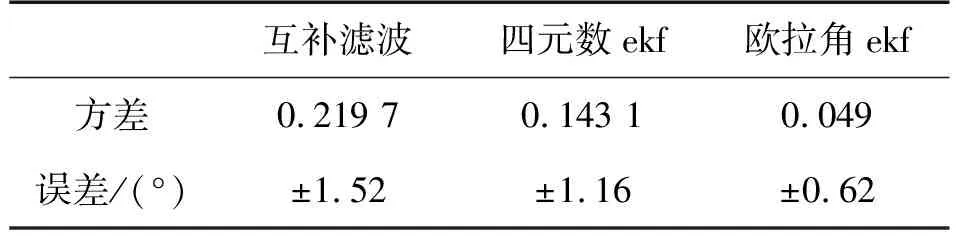
表1 差值比较
从结果数据可以看出,相比于只进行互补滤波处理,当结合EKF进行滤波处理时,可使数据解算效果得到有效提升,由于对解算的不同阶段运用EKF带来的效果不同,在解算前期时由于信号状态信息不完全,运用EKF滤波效果相比在解算后期运用EKF效果差。所以对欧拉角结果运用EKF可使解算误差和随机噪声的方差得到更有效降低,姿态数据波动进一步减少,最终解算精度也得到有效提高。
5 结论
通过本文研究,可以看出,采用互补融合EKF的组合滤波效果相比单一互补滤波效果更优,能有效降低解算结果误差,抑制噪声波动,使解算结果更稳定平滑,解算精度得到明显提高,也更能满足姿态的实时变化。且对于在互补滤波前期四元数解算时运用EKF的矫正效果不及在后期对欧拉角矫正效果明显,在后期运用EKF的滤波效果比单一互补滤波的效果提升一倍左右。

