基于欧拉—伯努利刚度矩阵的减摇鳍轴升力检测分析

孙明晓，栾添添，梁利华，刘彦文

（1.哈尔滨理工大学 自动化学院，哈尔滨 150080；2.哈尔滨工程大学 自动化学院，哈尔滨 150001）

0 引 言

航行于海上的船舶，受风、浪、流等干扰影响，不可避免地会产生六自由度运动，其中横摇尤为剧烈。不仅影响适航性及船载设备可靠性，而且大幅降低船体安全性与乘员舒适度。对于水面作战舰艇而言，直接影响武器精度，威胁战场生存能力[1-2]。因此，如何提高横摇稳定性成为船舶领域长期关注的研究热点。

近百年来，经过国内外学者与科研人员不断探索与尝试，减摇技术得到长足发展，减摇鳍成为迄今应用最为广泛的主动式减横摇装置。理论减摇效果可达90%以上，但实际工程中却很难实现。究其原因，主要是因为目前减摇鳍系统研究中，一般采用鳍角反馈控制方式。由于鳍角信号易于测量，检测装置简单可靠，且位于船体内部便于维修更换，实际工程中得到广泛运用；但其建立在简单定常流场水动力特性基础上，估算静态升力，不能真实反映鳍在海水中受到复杂动态水动力状况，两者的偏差限制了单纯依靠鳍角控制策略来提高减摇效果[3]。因此，如何用直接检测实际升力来代替估算升力成为亟待解决的难点。

现今，减摇鳍升力反馈控制技术研究仍方兴未艾，虽有少数海洋强国掌握，但详尽完整的理论分析文献尚未见刊，核心工程技术资料更是无迹可寻。美国Sperry公司最早提出升力反馈的概念[4]，设想在中空鳍轴内安装检测装置，构思巧妙；但在狭小的轴内安装、检测与维修异常困难，一直没能实现推广应用。英国Rolls-Royce公司采用在十字轴体内装应变片[5]，根据其受力来换算升力；但安装位置特殊，易损坏难更换，每次维修均需要船上坞，经济性差，且只适用于收放式减摇鳍，实用性与通用性不佳。日本三菱重工在驱鳍转动的液压伺服系统中安装压力传感器[6]，配合水动力压力中心等参数测量升力，不需做太大改动，维护容易；但所需参数具有很强的非线性，与鳍型、角度、角速度和航速等有关[7]，还需深入探讨研究。哈尔滨工程大学船舶减摇与控制研究所设计了基于上轴承负荷升力测量法[8]，在减摇鳍箱体上开方孔安装微型座与压力传感器；但对加工装配精度要求很高，且需设计专用传感器，工程实现不易。本文结合实际装船的常规减摇鳍和Sperry方案，在其基础上进行改进，寻求实用可靠的检测实际升力的方法。

1 鳍角反馈偏差原因分析

1.1 装备减摇鳍的船体横摇运动模型

根据Conolly理论，当横摇角较小时，装备减摇鳍的船体横摇运动模型[9]可表示为：

式中：Ix为横摇转动惯量，ΔIx为附加阻尼惯量，φ为船体横摇角，Nμ为阻尼系数，D为排水量，h为横稳性高，Kω为海浪扰动力矩，Kc为减摇鳍控制力矩。

若减摇鳍产生的控制力矩完全抵消掉海浪的扰动力矩，则船体停止横摇运动，即Kc与-Kω相等时，则横摇为零。因此，减摇鳍能否产生精准的控制力矩成为减横摇的关键。而控制力矩需要根据海浪的扰动力矩来判断，但海浪是无规则随机运动且海洋环境异常复杂恶劣，如何准确有效地检测实际升力成为一个难题。

当鳍在水中与流体成攻角α时，其受力情况如图1所示。图中1为船体，2为减摇鳍，一般成对安装于船体两侧舭部。V为来流速度，P为单鳍受到的水动力合力。按作用与结构将其分解可得升力Lα，阻力D，法向力N和切向力T。

各力之间存在如下关系：

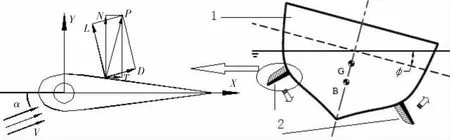
图1 鳍安装位置及受力示意图Fig.1 Installation position and force diagram of fin

因为对船体起扶正作用的是升力，则控制力矩可表示为：

式中：Lα为单鳍上的升力，l为鳍上水动力压力中心与鳍轴的距离，ε为鳍轴轴线于自鳍中心至穿过船重心纵轴垂线间夹角，通常很小，可以忽略不计。

这样，减摇鳍系统的控制难题就转化为如何精准检测实际升力的问题。

1.2 鳍静态升力偏差分析

鳍角反馈控制中，升力是根据鳍静态水动力特性，即鳍角与升力映射近似呈线性关系。但鳍在海水中绕轴不断转动，具有很强的动态特性，鳍角与升力不再是简单的线性关系，而呈严重的非线性。当船速恒定且鳍与水流成固定角度时，升力将保持不变，如下式所示[9]。

式中：ρ为流体密度，V为来流速度，A为鳍的投影面积，CL（α）为升力系数。

根据（4）式中影响升力的参数，具体分析产生偏差的原因。

（1）升力系数CL（α）。当鳍在定常流场中往复运动时，由于鳍的前缘动壁效应，随着无量纲频率Kt的增加，升力特性变得异常复杂。产生这种效应是因为鳍的功角增大时，鳍吸力面上流速加快，从而升力随着变大并推迟失速角，反之亦然。因此，鳍的静态和动态升力曲线并不会吻合，根据哈尔滨工程大学船舶减摇与控制研究所的动态水动力水池试验[10]可知，升力与鳍角间不是简单的线性关系，而是呈现一种梭形闭曲线。

（2）来流速度V。对于随船运动的鳍来说，应是流体与船相对速度。但在实际应用中，相对速度很难测量，一般利用航速来代替，必然造成偏差。

（3）流体密度ρ。不同海域的水密度是不一样的，船在行进中，所处流体密度是动态变化的，对估算升力造成一定的偏差。

另外，减摇鳍装船后水动力特性还受到其它因素干扰。归纳起来，传统的鳍角反馈式减摇鳍在原理上还忽略了以下问题：

（4）鳍角α、来流雷诺数Re，鳍弦长弗汝德数Fr和鳍升沉弗汝德数Fr等参数均不是恒值，而是随船实时变化，具有不确定性。在减摇鳍系统工程设计中，升力系数不是鳍在海水中的动态系数，而是通过水池试验得到的静态系数，难以真正满足动力相似原理，控制系统设计很难达到最优化。

（5）鳍的运动包括前向、绕鳍轴转动以及船体多自由度耦合运动，这些运动引起复杂的非定常振动，使鳍的水动力特性发生巨大变化，而静态估算不考虑这些因素影响。

（6）船体横摇、纵摇、横荡、垂荡等对升力的影响，可以等效为斜流角Δα。对于不规则波，一般大量统计斜流角后计算方差取平均值。实际海浪中，很难实时测得斜流角。在鳍角反馈系统中，检测的仅仅是鳍的转角，而非斜流角。

（7）船体、舭龙骨等对鳍的水动力特性产生干扰，鳍一部分处于船体边界层中，这部分的水流速度小于来流速度，使鳍的水动力偏高，常规减摇鳍不能反映这些影响因素。

（8）对于多对鳍的减摇鳍系统，前鳍与后鳍之间互干扰，后鳍受前鳍下洗流影响，实际水动力往往要下降。

综上所述，由于众多干扰因素的影响，鳍的实际升力比水池试验还要复杂。因此，造成估算的静态升力与实际的动态升力之间存在较大偏差，直接导致控制力矩的偏差，难以准确抵抗海浪扰动力矩，必然降低减摇鳍的减摇效果。同时，还会影响系统合理的能量分配，引起不必要的消耗。

2 升力反馈减摇鳍轴设计

鳍角反馈控制存在的本质缺陷，导致传统减摇鳍的减摇性能遇到瓶颈，需要从根本的原理入手寻求突破。因此，研究减摇鳍系统，应建立在实际动态水动力基础上，从工程应用角度出发，寻求简单可靠的方法，通过改进原有减摇鳍轴机构实现升力的检测。

2.1 轴的组合结构

减摇鳍系统的轴通过上支撑角接触滚子轴承和下支撑调心滚子轴承安装于箱体，箱体则焊在船体舭部。摇臂与轴相固定，连接驱动其转动的液压伺服装置，使轴按设定的控制方式转动。轴的外端用轴套安装鳍，伸入海水中。

轴为中空式，内部配有一实心轴芯，轴芯外端与轴固定，两者紧密配合且随轴转动。轴内侧设计可拆卸的端盖，如同瓶子的盖子。在端盖内侧沿鳍法向和切向安装两个非接触位移传感器，轴上安装测量鳍角的角度传感器，由于端盖可拆卸且位于船体内部，易于安装检修和更换。设计的轴组合结构如图2所示。

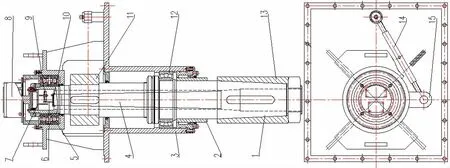
图2 减摇鳍系统转轴组合结构图Fig.2 Shaft combined structure of fin stabilizers

2.2 轴受力分析

轴组合结构可大致分为外部轴壳和内部轴芯：轴壳在鳍套的内侧部分较细，外侧直至连接鳍部分较粗；轴芯在鳍套内侧部分悬空，外侧与轴壳紧密固定，可认为成一体。轴承和摇臂在轴壳上形成简支点，轴壳BC段可看成简支梁；在下轴承外侧部分悬空尺寸较长，轴壳CE段可认为悬臂梁；轴芯在D处固定，其AD段在内部形成悬臂梁。轴整体结构近似为简支梁和悬臂梁的组合方式[11]，简化结构如图3所示。

图3 减摇鳍轴简化结构示意图Fig.3 Shaft structure of fin stabilizers

鳍在海水中转动时，受到的水动力可近似看成作用于鳍压力中心的合力，产生弯矩，轴在其作用下发生微小弯曲变形。DE段轴壳和轴芯固定成一体，位于E处的轴变形会带动D处轴变形，其变形会使AD轴芯在轴内上翘。由于D处轴截面为环形，截面惯性矩较小，所以形变量相对较大。轴内为空心，空间足够大，对轴芯的上翘不产生约束限制。AD轴芯上翘状态形似杠杆，将D处因变形产生的转角通过结构关系转化到A点形变量hA。

2.3 轴的刚度矩阵分析

根据欧拉—伯努利梁理论[12]可知：受力弯曲前，梁的横截面垂直于纵轴，弯曲后其仍保持为平面且垂直于纵轴。理论上，只有梁受到纯力偶或常力矩时，这种情况才会发生。但在实际工程应用中，这是一个合理的假设，推导出的方程非常准确地预测了挠曲特性，在机械设备、桥梁等众多工程领域中得以验证。

由于减摇鳍轴结构复杂，不是普通的模型，不能直接套用简单挠曲线方程。运用刚度矩阵分析轴的挠曲特性，可以避开繁琐的微分方程推导。同时，将轴的挠度和转角等参数进行数字化，易于计算机有限元的数学建模、校核与仿真验证，且对后期工程设计、修改等提供理论支持。

（1）选择单元类型

用L代表梁长，对其节点用单元进行编号，假设两点，其转角、弯矩和受力分别表示为φi，mi，fiy。

（2）选择位移函数

假定沿单元长度的横向位移为：

由于每个节点有一横向位移vi和一小转角φi，所以上式用4个自由度表示立方位移函数是适当的。可以满足梁的基本挠曲理论和节点处的位移和转角连续条件。将其表示成节点自由度的函数：

用节点自由度求ai，并代入原式得：

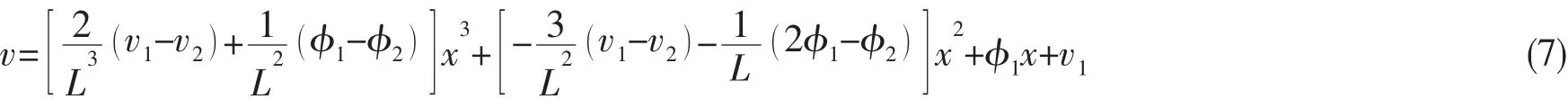
用矩阵形式表示为：

Ni称为梁单元形函数，是三次艾尔米特插值函数。对于梁单元，在节点1计算时N1=1，在节点2计算时N1=0。因为N1是和φ1相关的，在节点1计算时可从上式得出dN2/dx=1。形函数N3和N4对于节点2有类似的作用。

（3）定义应变和应力关系

由欧拉—伯努利梁理论[13]假定：变形前截面是平的，变形后仍然是平的，并转动一小角度，可得：

利用胡克定律σx=Eεx和上式可以得到挠曲应力公式：

（4）单元刚度矩阵方程

根据梁的基本理论，弯矩和剪力与横向位移函数是相关的，有以下关系：

式中：V为集中载荷，E为弹性模量，I为截面惯性矩。

将节点、剪力和弯矩关联起来：

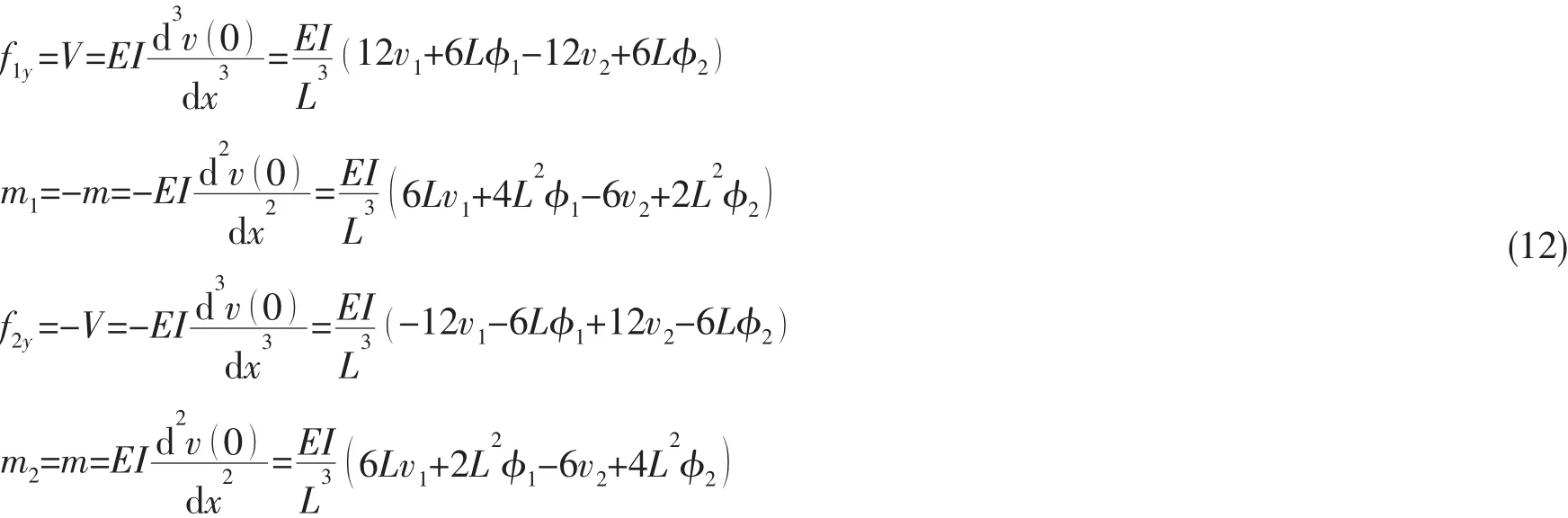
上式用矩阵形式表示为：

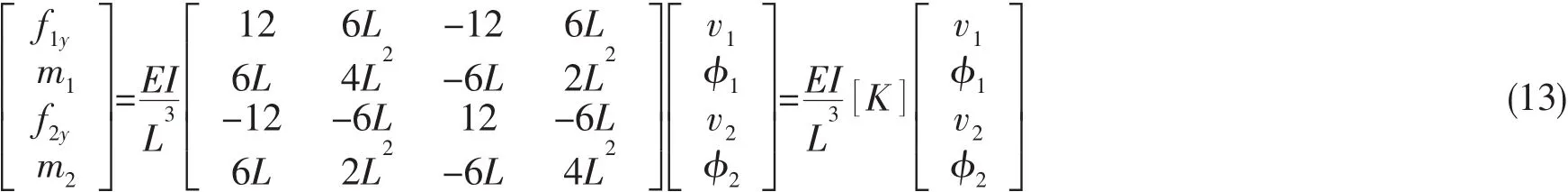
刚度矩阵建立力、弯矩与挠度、转角联系。忽略轴向效应，是因为梁长度L和高度hL的尺寸对于梁来说是比较大的，挠度作用的阶为（L/hL）3，而剪切作用的阶只有（L/hL），前者远远大于后者。这种情况下，用刚度矩阵来预测挠曲特性是完全可以的[14-15]。

由于减摇鳍轴各处横截面大小不一，所以惯性矩不相同，需将鳍压力中心处的水动力FE折算到轴D处。忽略上支撑点的影响，以轴芯及轴装鳍部分在C点形成单点支撑形式，则D处的等效受力为：

根据（13）式，建立轴壳CD悬臂梁段的刚度矩阵方程：

同理，建立轴壳BC简支梁段的刚度矩阵方程：

谈到京东物流目前正在搭建的全球智慧供应链基础网络建设（GSSC），王振辉表示，这是从简单追求点到点搬运效率，到从预测、采购、生产、物流交付的全链条优化；从实现国内的短链触达，到在全球范围内将优质供应链服务输出全球商家、消费者；京东物流致力于加速中国制造通全球，全球商品通中国，并给行业伙伴带来新的发展机会，实现可持续发展。通过GSSC，建设实体的通路网络与智能平台，推动供应链的无缝连接和快速反应，以达到商流、物流、资金流、信息流的协调通畅。

运用直接刚度法组装轴壳的整体刚度矩阵：

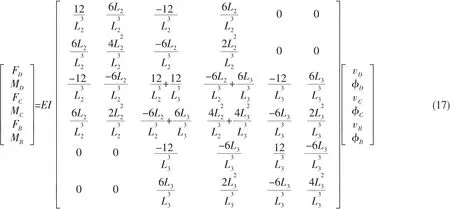
利用边界条件：vC=0，vB=0，φB=0，可得：

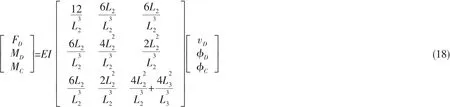
根据力和力矩平衡：MD=0，MC=0，将其代入上式，可得：

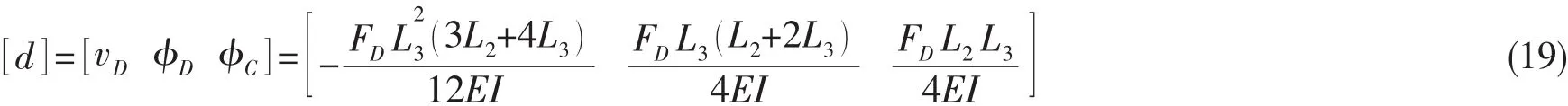
根据图3轴芯受力上翘时结构特点，可近似得：

进而可得，轴芯末端形变量hA与鳍水动力FE的定量关系：

式中轴空心处D点的环形截面惯性矩ID为：

式中：D为轴空心处的外径，d为相对应的内径。

总结刚度矩阵［K］的特性，适用于有限元一般性，可为其他类似问题分析提供理论依据。

（1） ［K］是对称方阵，其将相同数目的力和位移关联起来，且每一项都是对称的，符合互换定律。

（2） ［K］是奇异阵，施加充分的边界条件以消除奇异阵，并防止刚体移动之前，不存在逆矩阵。

（3） ［K］的主对角项总是为正，否则一个正向的节点力Fi可能产生负向位移ui，与实际结构的物理特性相悖。

（4） ［K］是半正定的，即对于非零实数矢量 ｛x｝，｛x｝T［K］｛x ｝＞0。

3 升力检测分析

3.1 传感器安装方式设计与分析

为了能够从动态水动力中直接分解出对减摇真正起作用的升力，需要对传感器的安装方式进行设计。但在狭小的轴内安装检修测量异常困难，为此设计可拆卸的端盖，用螺栓固定于轴壳末端，使其成为密闭空间，避免杂物进入，防止引起不必要的干扰。端盖内侧安装非接触式位移传感器，不受力碰撞不易损坏，检修时只需将端盖拆开即可，方便实用。

根据（2）式可知，升力L与法向力N、切向力T之间有力学关系，所以在端盖上沿鳍横剖面的法向安装一个传感器，检测轴芯末端的法向位移，切向安装另一个传感器，检测轴芯末端的切向位移。在轴芯对应位置上安装传感器感应体，如图4（a）所示。

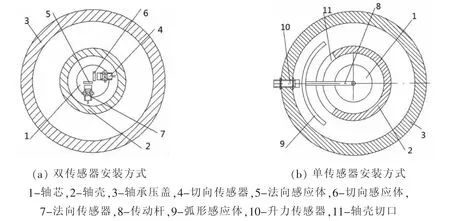
图4 两种传感器安装方式示意图Fig.4 Two installation methods of sensors

由于升力作用线垂直于水流相对速度和鳍轴的轴线，即升力的作用方向可根据这种关系确定[11]。因此可以改进为单传感器直接检测升力方向轴芯的位移。由于轴是不断转动的，为了避开转动的干扰，需将传感器固定于船体上，不随轴转动。

基于以上分析，可直接检测升力方向的轴芯末端位移量。轴结构不变，只在轴芯末端安装直角型传动杆，在轴壳上剖一弧形切口，使传动杆不但能够穿过轴壳，还要在轴转动时不碰到轴。在传动杆末端安装一弧形感应体，轴芯在水动力的作用下，在一定区域内转动和弯曲，但都落在弧形感应体的检测范围中。沿升力方向，在轴承压盖侧壁开一孔固定传感器，如图4（b）所示。

3.2 主要影响因素分析

根据（2）和（21）式可得，双传感器检测法向力、切向力与轴芯位移的定量关系为：

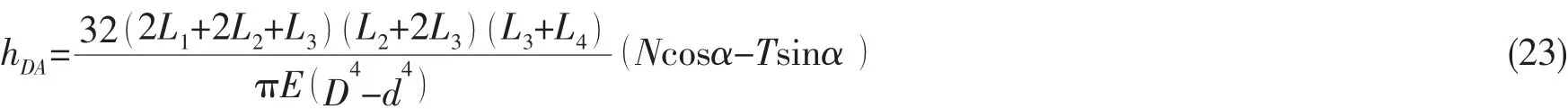
单传感器检测升力与轴芯位移的定量关系为：

因此，要想提高检测升力的准确度，就要分析影响轴芯末端位移量的因素。通过上式可见，有三种影响因素：一为轴各部分的结构长度Li；二为轴的材质，由弹性模量E决定；三为轴空心处的截面惯性矩ID，由轴横截面形状尺寸决定，因轴截面为环形，即由外径D、内径d决定。

为了降低对传感器分辨率的要求、提高检测精度及减小传感器选用难度，需使轴芯末端位移尽可能的大。对应主要影响因素可得，位移增大有三种方法，以单传感器检测法为例：

（1）增加轴长度

由于L2、L3、L4关系到结构强度，若改变要重新考虑强度是否适合，轴整体尺寸可能都要随之变化，不能轻易变动。而L1是轴芯悬空部分且延伸到船体，不影响结构强度，若船舱内空间允许，可适当增加其长度。

（2）减小弹性模量E

轴的材质决定弹性模量E，在保证强度的基础上，选择弹性模量小的材料制作轴。

（3）减小轴空心处的截面惯性矩ID

在保证强度的基础上，减小空心处的轴外径D或增大轴内径d，使环形截面惯性矩ID变小。

3.3 理论计算与仿真验证

（1）为了证明检测方法的正确性和实用性，以实际装船的某型减摇鳍设计参数为依据，以此为基础，设为模型1，结构尺寸如表1所示。

表1 转轴模型1设计参数Tab.1 Design parameters of model 1

（2）在模型1基础上，依次改变参数L1、E、ID，增大L1为1 165 mm，控制其它参数不变，设为模型2。

（3）改变模型1中AISI5150号合金结构钢材质，为了对比明显，选用工程合成树脂ABS，减小弹性模量E为2 495.9 N/mm2，控制其它参数不变，设为模型3。

（4）增大空心处轴内径 为200 mm，减小截面惯性矩ID，控制其它参数不变，设为模型4。

根据给出的量化关系进行理论计算，并进行有限元仿真分析验证[16]，各模型的减摇鳍转轴仿真情况如图5所示。

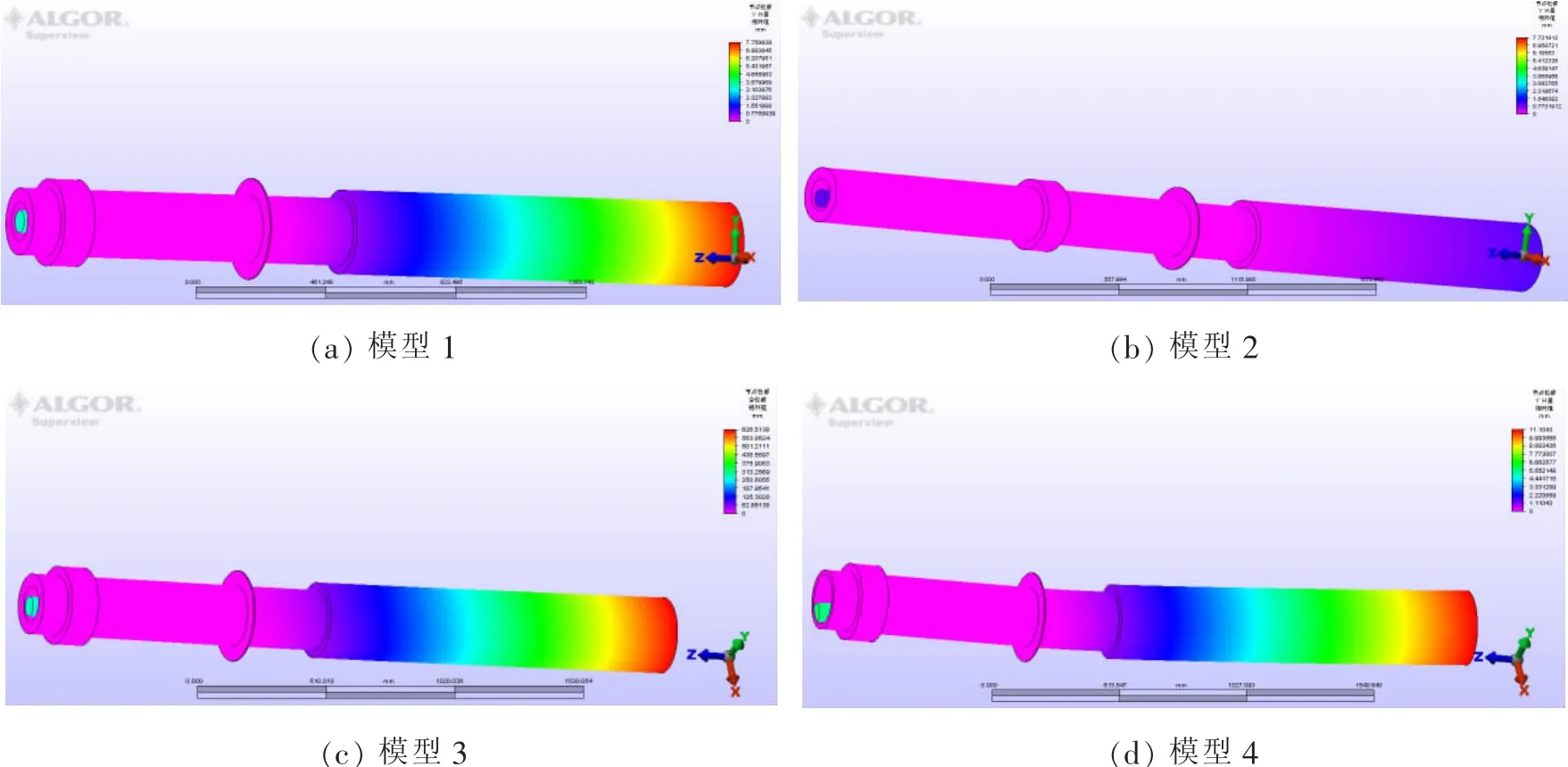
图5 空心转轴各模型仿真图Fig.5 Simulation diagram of the hollow shafts

统计计算与仿真的轴芯末端的位移，汇总成表2所示。

表2计算和仿真结果对比可得：

设计空心轴结构和升力检测方法是有效的，证明给出的升力与位移的量化关系是正确的。

影响位移的三个主要因素：轴的结构长度Li、材料的弹性模量E和轴空心处的截面惯性矩ID，改变其中一个，结果相应随之改变，计算和仿真的结果接近，验证了设计的合理性和正确性。

两者存在一定的偏差，是由于理论分析时假定轴近似为一条细长的刚性梁，摇臂、轴承近似为简支点、转角与三角关系近似相等，而实际减摇鳍轴形状复杂且体积庞大，各截面惯性矩不尽相同，密封等处受力，干扰影响因素较多，导致一定的偏差。后期工程机可根据理论推导的量化关系进行具体校准修正，进一步减小偏差，使其更逼近实际工程。

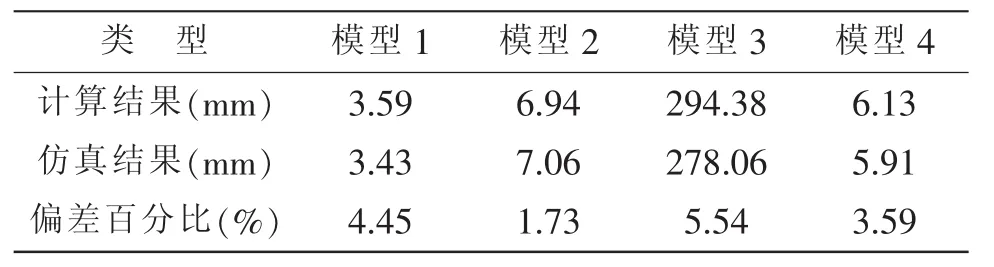
表2 各模型计算与仿真结果Tab.2 Calculation and simulation results of models

4 结 论

（1）分析鳍角反馈偏差产生的原因，避开众多干扰和粗略估算，直接在实际装船减摇鳍轴基础上设计空心轴，使其兼顾检测机构的功能，改动小，易于工程实现，实用性强。

（2）运用欧拉-伯努利梁刚度矩阵对轴进行理论分析，得到升力与轴芯末端位移的量化关系。

（3）设计可拆卸的轴端盖，方便传感器安装校准检修，同时形成密闭空间避免杂物干扰，给出两种传感器安装方式，简单实用。

（4）分析影响轴芯位移的主因，以实际减摇鳍设计参数为依据，通过计算和仿真，证明量化关系的正确性和主要因素的影响趋势，为工程设计及改进提供理论支持。

（5）采用非接触位移传感器，检测轴内的相对位移量，不受外力碰撞干扰，不易损坏，通用性强。

（6）鉴于创新性、实用性和经济性等诸多优点，升力反馈研究对减摇鳍技术整体发展具有标志性意义，作为船舶减摇领域新兴事物，其应用前景及市场价值亦将更具潜力。另外，船舶运动控制领域中，广泛应用舵、T型水翼、压浪艉板等多种控制水翼进行减摇，直接准确地检测其动态水动力是一个普遍难题，因此可为其它水翼轴设计改进提供借鉴。