多种运动模式下水下机器人导管螺旋桨的敞水性能研究

陈 原，于 飞，李 静

（1.山东大学（威海）机电与信息工程学院，山东 威海 264209；2.烟台工贸技师学院，山东 烟台 264000）

0 引 言

导管螺旋桨在载荷较重的船舶和水下机器人推进器上得到了广泛应用。它不仅具有较大推进力和高效姿态调整功能，而且有利于减小船舶和水下机器人的整体振动，故对导管螺旋桨推进性能的研究对提高船舶和水下机器人的机动性有着至关重要的作用。

随着求解雷诺平均Navier-Stokes方程技术的发展，利用计算流体动力学（CFD）方法，求解水下机器人的压力分布和作用在流体上的推力及其转矩等越来越普遍。最近几年，CFD方法经常被用于预测船舶和水下机器人的性能。例如，Mansoorzadeh[1]，Lee[2]和Tang[3]等人利用单相流模型研究了浸没船只的水动力性能。Tyagi等人[4]通过CFD方法仿真计算出了一定攻角条件下作用在水下船体上的推力和转矩。Phillips等人[5]利用CFD方法预测了水下机器人的非定常性能。Hayati等人[6]利用CFD方法，对水下机器人螺旋桨在不同攻角条件下的推力、转矩和推进效率进行了研究。

然而，将CFD方法应用于水下机器人导管螺旋桨推进性能研究的还相对较少。欧礼坚等人[7]运用FLUENT软件模拟了粘性流场中导管螺旋桨在不同进速系数下的推力系数和转矩系数。该研究虽然证明了CFD方法应用于导管螺旋桨推进性能研究的可行性，但是其中的导管螺旋桨类型和水下运动模式太过单一（仅包括直航运动）。李超等人[8]利用 FLUENT软件对拖网渔船的导管螺旋桨进行了研究，在保持螺旋桨形状不变的情况下，改变导管的长径比、收缩系数和伸张系数三个形状参数，分别计算出了它们的敞水性能，进而研究了导管参数对推进器推进效果的影响规律。但是，该研究缺乏其他运动模式下不同导管对螺旋桨推力影响的探索，也就无法进一步提高螺旋桨的推进性能。Barros等人[9]研究了攻角的大小对水下机器人操纵性能的影响，而忽略了螺旋桨对水下机器人的作用，实际上螺旋桨和导管间存在相互作用，这就与实际情况不符。

本文使用成本低且效率高的CFD方法，研究了不同导管桨在多种水下运动模式下的推进性能。为了探索导管类型对导管桨的影响，本文将Ka4-70螺旋桨与三种型号（JD7704,、NO.19A和JD75）的导管相匹配，分别研究了直航、斜航和后退等多种运动模式下螺旋桨的敞水性能，并对桨叶的弦向压力分布、螺旋桨表面的压力分布和速度分布进行了仿真研究。

1 数值计算方法

本文假定流体是恒定不可压缩的，因此流动控制方程中不涉及到能量守恒方程，仅涉及到质量守恒和动量守恒两个方程。其中，质量守恒方程的数学表达式如下：

由于计算机的容量和计算速度的限制，直接求解瞬态三维N-S方程通常难以实现。一般将控制方程进行统计平均，使其无需计算各尺度的湍流脉动，只需计算出平均运动。这样就降低了空间与时间的分辨率，从而减少了计算工作量。雷诺平均N-S方程的表达式如下：

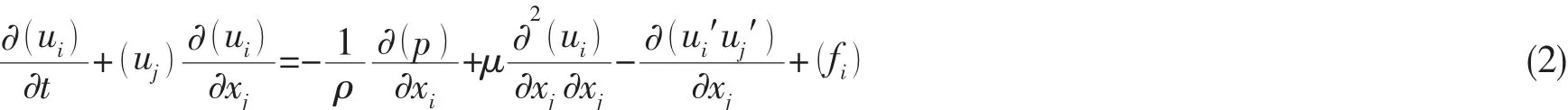
式中：ui是在笛卡尔坐标系下xi（i=1,2,3）方向上的时均速度分量；t为时间；p为时均压力；ui′是笛卡尔坐标系xi（i=1,2,3）方向上的脉动速度分量。

湍流流动是自然界中较普遍的流动方式，k-ε模型和k-ω模型都是常见的湍流模型。k-ε模型的计算量适中且有较多的数据积累，但是其过高估计了尾迹区的湍流应力，从而会导致分离的边界层及较差的逆压区。而k-ω模型对壁面边界层，自由剪切流和低雷诺数流动性能良好，但是对自由来流的湍流耗散率过分依赖。结合两个湍流模型的优点，本文将在核心区采用SST k-ε湍流模型，而在近壁面区应用k-ω模型。另外，压力—速度耦合方式采用SIMPLE算法，压力离散方式选择为Standard方式，动量、湍流动能和特定耗散率均采用二阶迎风式的离散格式，来流湍流强度设置为5%。为了提高仿真结果的精确度，连续性、动量、湍流动能和湍流特定耗散率收敛标准均设置为10-4。

在本文的数值仿真模型中，攻角（流体入流方向和螺旋桨主轴在x-y平面内的夹角）表示为β，所采用的惯性坐标系定义如下：x轴正方向表示入流方向，与直航时螺旋桨的旋转轴平行；y轴正方向表示上方，z轴方向符合右手定则。为了描述螺旋桨的敞水性能，引入了进速系数的概念。螺旋桨负载随着进速系数的增大而减小。进速系数J的取值取决于入流速度值U，它们之间的关系如下：J=U/nD，U=。其它几个与导管和螺旋桨有关的参数定义如下：其中，KTN、KTP分别表示导管推力系数和螺旋桨推力系数，KT，KQ，η分别表示导管螺旋桨总推力系数、螺旋桨转矩系数和导管螺旋桨的效率。

2 CFD数值仿真和仿真结果分析

本文所使用的螺旋桨为Ka4-70，其主要尺寸参数如下：直径0.25 m，桨叶数4，螺距比1.2，侧斜0°，纵倾0°，盘面比0.7，轮毂比0.67。本文中涉及到JD7704、NO.19A和JD75三种导管。此外，螺旋桨的转速、叶梢速度 U、流体密度 ρ参数定义如下：n=10 rps，U=nπD=7.85 m/s，ρ=998.2 kg/m3。将螺旋桨的半径L=0.25 m作为特征尺度。

2.1 网格划分和计算方法的验证

导管螺旋桨的三维计算区域如图1所示。为了得到螺旋桨周围的流场仿真数据，将螺旋桨置于一个小圆柱内。为了方便细化网格同时提高计算效率，将小圆柱和导管同时置于一个以6L为边长的正方体流域内。剩下流域为外流域，外流域设计为半径20L且高30L的圆柱形。所有仿真实例中的入口边界距离正方体流域边界为4L，出口边界距离正方体流域边界距离为20L。此外，仿真模型采用速度入口和压力出口，而螺旋桨、导管和圆柱流体侧面均采用无滑移边界。

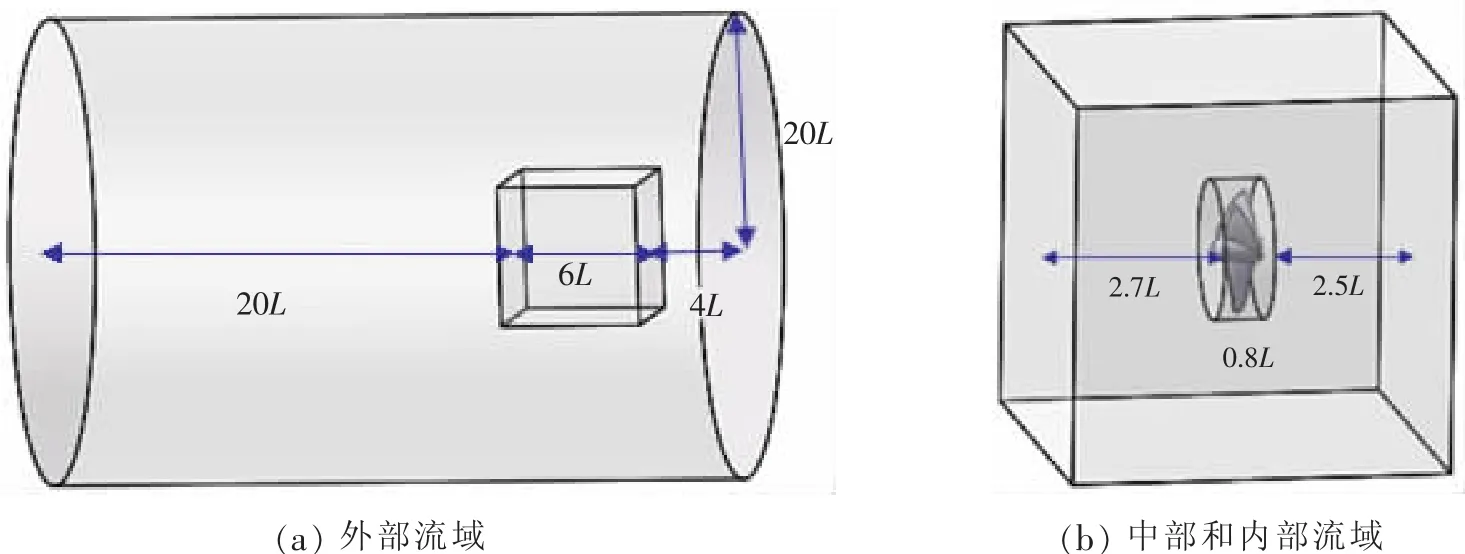
图1 计算区域Fig.1 Computational domains

如图2（a）-（b）所示为流域的网格划分，在外部流域使用了如图2（a）所示的网格质量更好的结构网格，而在中部和内部流域使用了如图2（b）所示的非结构网格，以适应较复杂的内容结构，两个网格之间通过设置interface连接。以直航时，Ka4-70+NO.19A组合为例，网格总数目为2 431 061，其中，四面体网格数目为2 103 059，六面体网格数目为64 106，三角形网格数目为255 156，四边形网格数目为8 740，螺旋桨表面的最大尺寸为2 mm，立方体流域的最大尺寸为20 mm。

为了验证计算方法的正确性，本文利用Ka4-70+NO.19A导管螺旋桨进行计算方法的验证，该类导管螺旋桨具有公开敞水试验结果，其试验结果见参考文献[10]。该导管螺旋桨敞水特性计算结果与试验结果对比如图2（c）所示。根据KT和KQ的计算值和试验值作比较，可以发现计算结果和试验结果吻合良好，误差均在10%以内，满足了工程上的需要，同时说明了使用该方法模拟导管螺旋桨敞水性能的可行性。

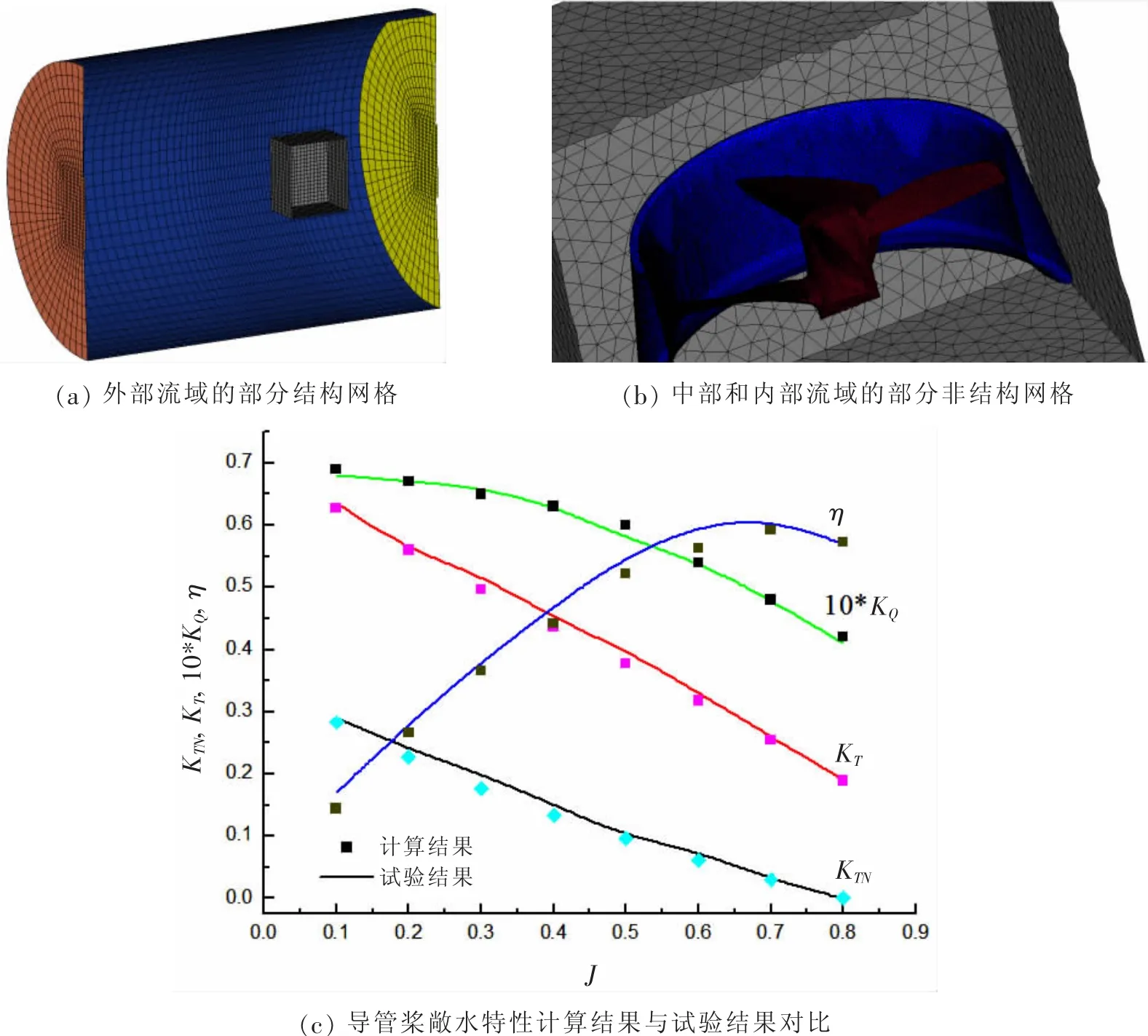
图2 网格划分和计算方法的验证Fig.2 Mesh generation and verification of computational method

2.2 数值仿真和结果分析

导管尺寸参数对螺旋桨的推力、转矩和水动力效率等有很大影响。为了探索导管类型对导管桨敞水性能的影响，本文在保证叶梢间隙为1 mm条件下，以Ka4-70螺旋桨与JD7704导管、NO.19A导管、JD75导管三种配合为例，就直航运动模式、斜航运动模式、后退运动模式下的模型进行了数值仿真，分别研究了螺旋桨的推力系数、转矩系数和推进效率，并对螺旋桨的弦向压力分布、桨叶表面的压力分布和速度分布进行了分析比较。

（1）直航运动模式

如图3所示为直航运动模式下不同导管对螺旋桨敞水性能的影响结果。从图3（a）-（c）可以看出，随着进速系数的增大，各推力系数和转矩系数逐渐减小；进速系数一定时，导管的类型对导管推力系数影响不是很大，但是对其他系数有影响：在整个进速系数范围内，针对总推力系数、螺旋桨推力系数和转矩系数，Ka4-70+JD7704组合总是小于另外两个组合。图3（d）显示，随着进速系数的增大，三种组合导管桨的推进效率都是先增大后减小，在进速系数达到0.6～0.7时，效率达到峰值；当推进系数较小时，三种组合的推进效率基本一致，而当推进系数达到0.6以后，Ka4-70+JD75的效率较其它两者稍有优势。

综上所述，在直航运动模式下，当进速较小时，三种组合方式推进效果接近，当进速系数较大时，选择Ka4-70+JD75螺旋桨与导管的配合更合适，推进效率更高。这是由于JD75导管的长径比大，整流效果好。

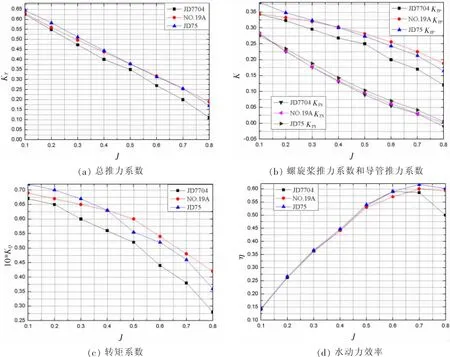
图3 直航运动模式下不同导管对螺旋桨敞水性能的影响结果Fig.3 Comparison between the open water performances of different types of duct propellers at β=0°

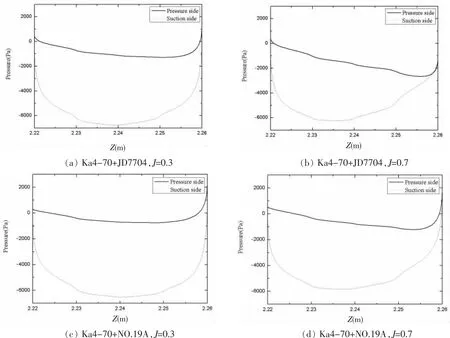
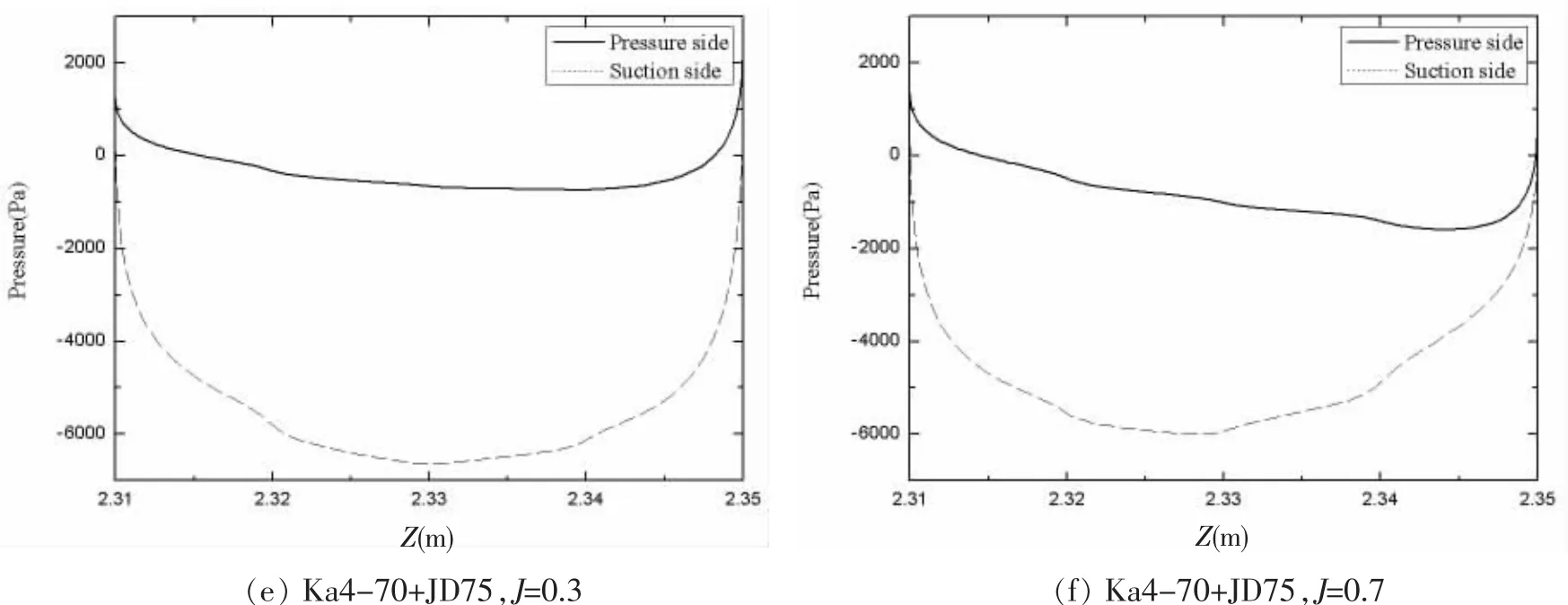
图4 r/R=0.7时，不同组合螺旋桨叶片表面弦向压力分布Fig.4 Chord wise distribution of pressure at r/R=0.7 in different combinations

为了探索螺旋桨压力侧和吸力侧的压差情况，利用CFD-Post提取螺旋桨表面压力数据，作出如图4所示的直航时不同组合导管螺旋桨弦向压力图。从图中可以看出，同一种导管桨组合，不同进速系数时，螺旋桨叶片表面的弦向压力分布不同，负载越大（进速系数越小）时，压力侧和吸力侧的弦向压力差越大；同样进速系数时Ka4-70+JD7704组合的弦向压力差始终最小，而螺旋桨旋转时，弦向压力差越大，叶片振动越剧烈，导致水下机器人的艇体振动越剧烈，最终影响整体运行。综上所述，直航时，选择弦向压力差普遍较小的Ka4-70+JD7704组合更稳定。

（2）斜航运动模式

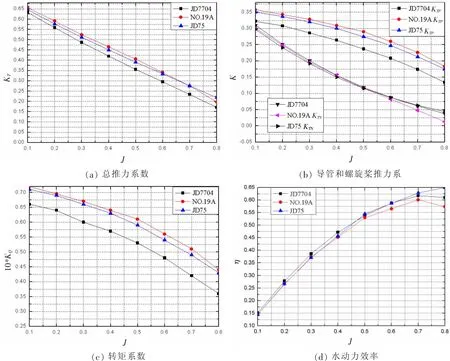
图5 攻角15°斜航运动模式下不同导管对螺旋桨敞水性能的影响结果Fig.5 Comparison between open water performances of different types of duct propellers at β=15°

为了研究导管螺旋桨在斜航运动模式下的敞水性能，本文以攻角为15°的斜航为例，对不同导管对螺旋桨敞水性能的影响进行了仿真分析，仿真结果如图5所示。由图3、图5可以看出，无论直航还是15°攻角斜航，随着进速系数的增大，各推力系数和转矩系数逐渐减小。但当进速系数较大时，与直航相比，斜航时导管产生的推力更大，产生的总推力更大，需要的转矩也更大。由图5（d）可知，与直航相同，推进系数达到0.6之后，Ka4-70+JD75的效率较其它两者略有优势。因此，可以得出如下结论：在15°攻角斜航时选择Ka4-70+JD75导管桨组合更合适，尤其是在进速系数较大，即负载较小的情况下。

为了更直观的展示斜航运动模式下，不同导管对螺旋桨敞水性能的影响，同样利用CFD-Post对仿真得到的数据进行后处理，得到螺旋桨表面的压力分布如图6所示。从图中可看出，同一个螺旋桨的三个桨叶表面的压力分布不完全相同，而与入流速度和桨叶位置有关，同一个螺旋桨的一片桨叶中心的压力小于边沿的压力，左侧桨叶表面压力小于右侧桨叶表面压力。三种情况中，均是进速系数0.7时桨叶叶面压力大于进速系数0.3时；无论进速系数为0.3还是0.7，桨叶叶面压力相互关系均是NO.19A＞JD75＞JD7704。以上关系均和图5（b）中导管桨中螺旋桨推力系数曲线走势一致。

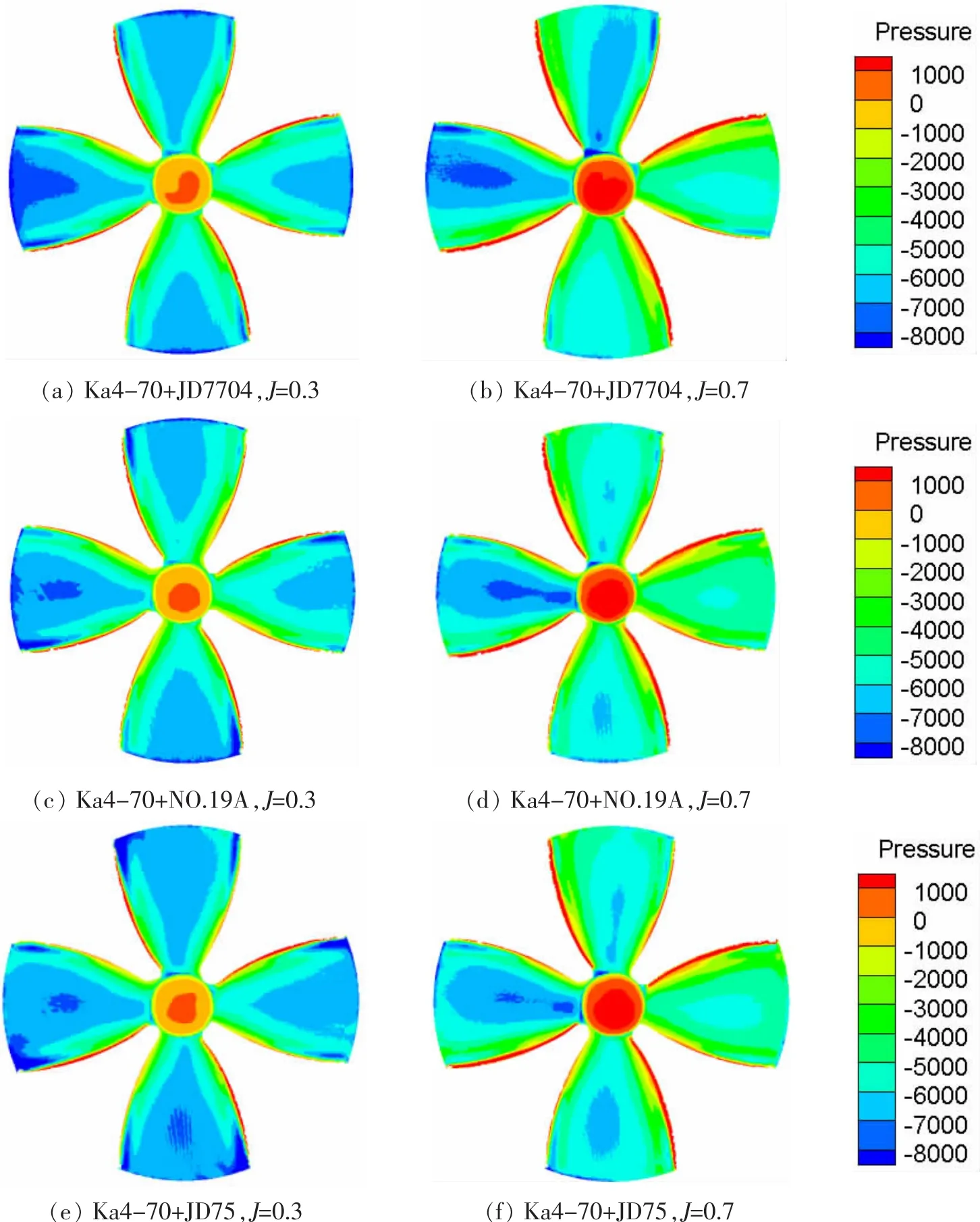
图6 攻角15°斜航运动模式下不同导管螺旋桨桨叶压力分布Fig.6 Pressure distribution on pressure side of propeller blades at β=15°

（3）后退运动模式

水下机器人除了直航和斜航运动外，在一些特殊情况下需要后退。在保持叶梢间隙为1 mm的条件下，本文对三种导管桨在后退模式下敞水性能进行了研究。为了研究后退运动模式下入流速度和导管尺寸参数对螺旋桨叶片表面流体速度的影响，利用Tecplot对仿真得到的数据进行后处理，得到螺旋桨入流叶面在入流方向（z轴正方向）上流速如图7所示。从图中可以看出，流体速度从导边到随边呈下降趋势；同一种导管螺旋桨，进速系数大时，叶片表面z轴正方向上的流体的流速就更大；J=0.3时，JD7704组合表面的整体流速更小；J=0.7时，JD75组合整体流速更小。更重要的是，流速范围越小，流速越均匀，运转越稳定，噪声越小，所以后退时，Ka4-70+JD75组合更安静，隐蔽性更好。

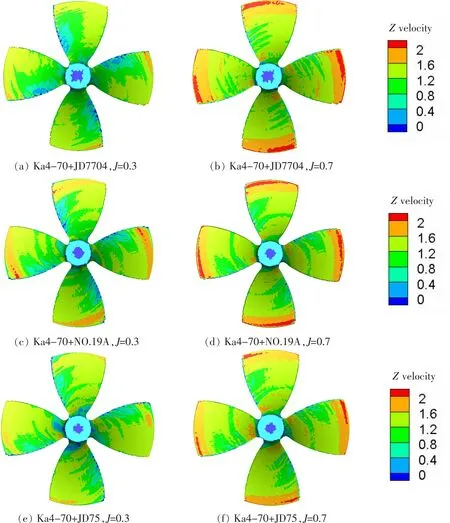
图7 后退时螺旋桨入流叶面的流速分布Fig.7 Distribution of the inflow velocity on propeller blades while performing backward motion

3 结 论

本文在保持螺旋桨叶梢和导管内壁间距为1 mm的前提下，就三种运动模式下不同类型导管对螺旋桨敞水性能的影响进行了研究，得出以下结论：

（1）直航和以15°攻角斜航情况下，进速系数较大时，Ka4-70+JD75组合效率更高。

（2）直航运动模式下，Ka4-70+JD7704组合桨叶弦向压力差小，桨叶振动微弱，螺旋桨旋转更稳定，整个艇体运行更平稳。

（3）斜航运动模式下，压力侧的叶片压力分布与入流速度和桨叶位置密切相关。同时，进速系数越大，桨叶叶面压力越大。不同导管桨的螺旋桨表面压力大小关系和导管桨中螺旋桨推力系数曲线走势一致。

（4）后退运动模式下，螺旋桨表面流体速度从导边到随边呈下降趋势，Ka4-70+JD75组合桨叶表面流速范围相对较小，产生的噪音小，隐蔽性好。