GPS掩星大气探测中数据的平滑处理方法分析
周冰,李玉立
(1.广州市增城区国土资源测绘院,广东 增城 511300;2.河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室,河南 焦作 454000)
1 引 言
GPS掩星是一种主动遥感大气探测技术,与气象卫星、雷达和无线电探空气球等遥感技术相比较,其是目前唯一能够提供全球均匀分布、高垂直分辨率温、湿、压观测剖面的大气探测技术,并具有实时、全天候、低成本、高精度等多种优点。由于不均匀的密度、温度、水汽、压强及折射率等大气参数的存在,使得观测得到的掩星观测数据并不能直接使用,因此需要对数据进行降噪平滑处理,此时,对于数据平滑处理方法的选择就显得尤为重要。
对于GPS掩星原始数据,由于P1码和P2码随时间变化相位延迟的存在,会混杂噪声数据,包含测量观测中的随机误差以及仪器的系统误差。对于同样条件下同一测量方案来讲,系统误差可以通过计算消除影响;随机误差是由各种各样的偶然因素造成的,其与测量真实值纠缠在一起,此时使用数据平滑的方法能够尽量剔除噪声,使得平滑后的数据无限地接近真值,最后利用这些更加准确的数据进行下阶段的运算。对于GPS掩星观测数据的研究多种多样,其中,柳聪亮等对GPS掩星大气探测中观测数据的残差进行了仿真研究,研究了双频线性组合法对误差的改正[1];徐晓华利用GNSS无线电掩星技术进行大气探测,指出我国目前掩星大气探测中数据的处理方法[2];乐新安等对近地空间环境的GNSS无线电掩星技术的发展作了介绍,并研究了最小二乘法在掩星数据中的应用[3]。显而易见,GPS掩星大气探测中数据的平滑处理方法为GPS掩星技术反演大气参数提供了强有力的数据处理理论支撑,对于需要探测大气参数相关的领域也有重要的实用价值。
本文首先对空基GPS反演大气参数的具体流程进行了图解分析,然后从理论层面与模型方法实用性两个角度对比分析了数据平滑方法,最后采用不同的平滑方法对一组掩星观测的原始数据进行适用性分析。
2 空基GPS反演大气参数具体流程
参阅相关资料[4~7]得出空基GPS反演大气参数的具体流程,如图1所示:

图1 反演流程图
本文对于数据平滑处理的研究主要是针对数据预处理部分,通过对平滑处理后数据的应用准确性来判断平滑处理效果的优缺点。
3 GPS掩星大气探测中数据的平滑处理方法
3.1 平滑方法
目前平滑方法种类繁多[8,9],对常用的数据平滑方法进行了分类,如图2所示:

图2 平滑方法分类
(1)局部平滑
局部平滑用于处理一些采样频率高、排列紧密的掩星观测数据;其计算公式相当于一个移动平均式,以一定的步长对每一个点进行处理,类似一个窗口从原始数据列划过去,因此也称为滑动或移动平滑法。区域长若取三点就是三点平滑法,区域长若取五点就是五点平滑法,此外还有七点平滑法;由于三点平滑取点太少一般只使用一次函数的平滑,因此平滑不理想,而七点平滑取点过多,容易平滑过度而造成不良影响,所以最常用的是五点平滑法。
(2)大范围平滑
它是把原始数据看作一个整体为进行平滑的手段。
①傅里叶平滑法是以傅里叶变换为基础,由于任何观测过程所得到的原始数据都是有限的,都可以以傅里叶级数形式打开,其级数可以表示为多项式求和形式,级数形式可以表现出观测变量的变化过程,而其中一些高次项多是由噪声引起的,因此起到数据的平滑作用。实际应用中,傅里叶平滑多用于图像的数据处理且效果更好。
②数字滤波平滑是以数字信号的处理理论发展出的,是目前为止应用最广泛的平滑算法之一。其主要采用低通滤波器的设计理念,即信号频率低于滤波器的截止频率时信号通过,信号频率高于滤波器的截止频率时则不能通过,由于截止频率时大多为噪声信号,这样便起到数据平滑的效果。
③曲线拟合平滑是以最小二乘原理为依据演变出的一个非常通用的算法,其可以通过给定已知函数、原始数据解决函数参数,从而得到一条消除噪声后的曲线。实际应用中,很多软件存有曲线拟合平滑方法的源代码,此方法能够很好地保持曲线的变化状态,但是容易忽略由小范围的参数或某些技术原因引起的细节变化。如果能根据实验数据建立经验公式,这一方法将更加实用,此时对于大范围平滑法应酌情使用。另外,曲线拟合平滑对于局部的少量数据平滑效果也不错。
(3)计算平滑法
计算平滑法可分为速度平滑法和加速度平滑法,主要是对速度变量和加速度变量的平滑效果更佳,多以差分计算的形式完成。
3.2 实验部分
接下来通过采用不同的数据平滑方法对表1中一组掩星观测的原始数据进行平滑结果对比,以分析数据平滑方法选取的问题。
(1)适用于曲线拟合平滑的多项式拟合法方法
曲线拟合法的目的是拟合出一条能够最大限度不失真的逼近测量数据的平滑曲线。此处利用多项式拟合法,对于测得的掩星数据进行公式化处理,通过计算构造出n次函数来近似地表达待处理数据的函数关系。在MATLAB软件中这些计算过程已被存储,可以通过调用函数命令polyfit,再通过算法编辑可以实现待处理数据的拟合,其命令形式为:
p=poltfit(x,y,n)
(1)
其中,x、y为已知数据,n为拟合多项式阶数,p为返回所得多项式的未知数系数。一般情况下多项式拟合的阶数越大拟合的精度越高。

已知数据前20点 表1
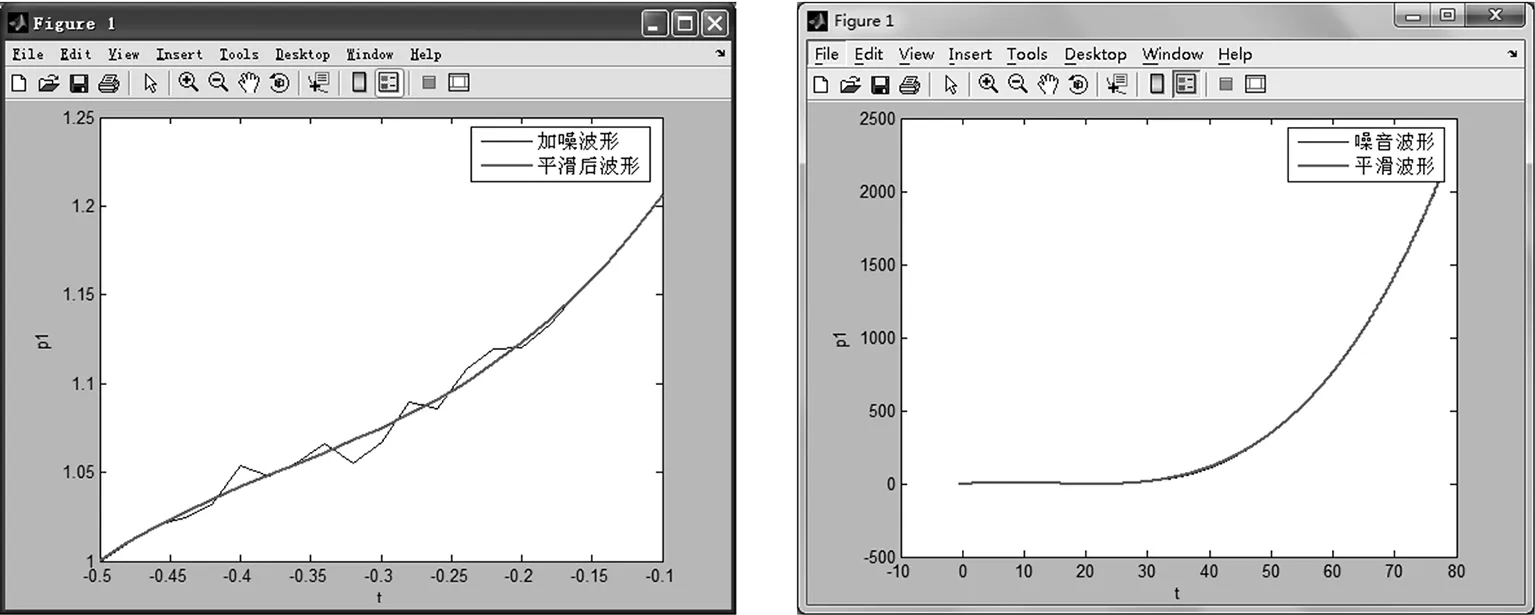
图3 多项式拟合法20点平滑图 图4 多项式拟合法全点平滑图

多项式拟合法前20点数据平滑结果 表2
对已知的所有数据进行平滑:

多项式拟合法全点平滑结果 表3
通过对比图3、图4及表2、表3可分析出:①根据图4可以看出p1载波的相位延迟随时间变化的姿态很明显,对图3可看出多项式法去掉了原始数据的噪音峰值。从图像上看,平滑得到一条曲线;从数据上看,平滑数据也和已知数据比较相似,原始数据基本没有失真。说明多项式平滑法既可适用于局部少量数据平滑也可以用到大范围的数据平滑。②对比全平滑数据的前20平滑点,可看出比原始数据所含误差还要大,数据失真严重,也印证了前文所提多项式平滑法的弊端,即如果数据过多却又不能匹配出多项式的参数,整个平滑算法将完全失真。因此在原始数据过多、无法得到经验公式的情况下建议不采用多项式平滑法。
(2)适用于局部平滑法的简单移动平均法拟合方法
简单的移动平均法拟合就是取时间序列n个连续观测值求取平均值,按照数据顺序依次移动直到将所有数据处理完毕为止,这时会得到一个平均值序列,从而达到一个数据平滑的效果,其计算公式可以表达为:
Mt=(Yt+Yt-1+...+Yt-k+1)/n
(2)
其中n为移动的平均周期数,表示了n阶的移动平均,移动平均它可以平滑数据,消除一些随机噪音干扰,让长期趋势凸显出来,从而可用于趋势分析和数据对比。


图5 移动平均法20点平滑图 图6 移动平均法全点平滑图移动平均法20点数据平滑结果 表4
对已知的所有数据进行平滑:

移动平均法全点平滑的前20点数据 表5
通过对比图5、图6及表4、表5可分析出:移动平滑法曲线相比于多项式平滑法曲线更趋于直线,其平滑效果并不如多项式平滑法;移动平滑法的数据虽有一小部分数据失真,但也消除了噪音峰值误差起到了平滑的作用;移动平滑法相当于一个求均值的算法,无论是算法编辑还是计算量上,移动平滑法都更容易实现,原理也更简单。
(3)适用于局部平滑及大范围的平滑的五点三次拟合平滑方法
五点三次平滑法融合了曲线拟合法的一个经验公式和最佳步长的移动平均法,从已知的所有数据中选取前20点进行五点三次拟合平滑方法实验。


图7 五点三次平滑法20点平滑图 图8 五点三次平滑法全点平滑图 五点三次平滑法20点数据平滑结果 表6
对已知的所有数据进行平滑:

五点三次平滑法全点平滑的前20点数据 表7
通过对比图7、图8及表6、表7可分析出:①五点三次平滑法相比前两种方法无论是平滑效果还是p1相位延迟随时间的变化状态都一目了然。②五点三次平滑法的平滑数据与原始数据对比,无论是局部的还是全部的基本没有失真,还很好地消除噪音峰值误差达到一个相对较好的平滑效果;但相对前两种算法,它的算法编辑更复杂,运算量更大,更容易出现算法错误。
4 结 论
本文通过多种方法分别对空基GPS掩星观测数据进行平滑处理,分析了不同条件下的GPS掩星技术反演大气参数的方法并得出结论。采用不同的平滑处理方法处理掩星观测数据会得到不同的拟合真值曲线,应根据实际需要进行平滑处理方法的选择,利用多项式拟合的经验公式可以对数据进行更加准确地平滑处理,但是耗时较长;利用移动平滑法则可以在有效时间内得出部分数据的最佳平滑处理;利用五点三次平滑则可以快速对数据进行不同精度的平滑处理。通过对空基GPS掩星观测数据进行平滑处理方法的研究,也必将促使GPS掩星观测在大气探测中发挥更大作用。

