基于多普勒法管道流量的测量方法研究

王晨，杨成禹，段洁，薛克娟

（1.长春理工大学 光电工程学院，长春 130022；2.长春大学 电子信息工程学院，长春 130022）

在流量的测量领域中，利用悬浮颗粒或气泡对超声波反射这一原理所研制的多普勒流量计，广泛地用于纸浆、泥浆、污水、工业排放水和农业用水等流体流量的测量中[1]。现有的多普勒流量计存在着许多不足，比如在测量上精度较低，尤其是在测量低流速或小口径方面，其测量精度均较低，这些缺点在一定程度上制约了多普勒流量计的推广及应用[2-3]。

许多学者为提高多普勒法流量计的测量精度做出了大量研究工作。但均是集中于提高多普勒信号的频谱分析及数字信号处理方面，很少结合圆形封闭管道内流体在不同流动状态下的流速分布特征来对管道流量进行有效的分析与测量[4-6]。目前市场上多普勒法流量计产品和相关研究论文，均是以多普勒信息窗内粒子反射出来的平均频率等效整个管道内粒子反射出来的平均频率来计算管道流量[7-10]。经研究运用平凹声透镜对发射束和接收束进行汇聚，使声束近似平行，缩小多普勒信息窗的体积，从而实现多通道分区域测量管道内粒子反射出来的平均频率。测量时通过结合圆形封闭管道内流体在不同流动状态下的流速分布，精确测量出流场中多个点的流速，从而实现管道内流体流量的精确测量[11-13]。

1 多普勒法测量原理

根据多普勒效应可知物体辐射的频率因波源和观测者的相对运动而产生变化。多普勒法测量流量原理图如图1所示。

图1 多普勒法测量流量原理图

图1显示分别将发射探头和接收探头安装在A、B两处，当发射探头发射出频率为f0的连续声波，声波受到随流体移动的悬浮颗粒和气泡的散射，接收到的信号频率f1略低于f0，频率差值即为多普勒频移。发射连续余弦信号如公式（1）所示：

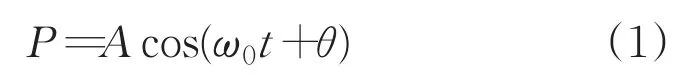
式中，P—发射连续声波的余弦信号；A—余弦信号的幅值；ω—余弦信号的角频率，即2πf0；θ—余弦信号的初始相位。

接收探头所接收到流体内一个悬浮颗粒或气泡散射后所形成的回波信号为如公式（2）所示：

回波信号P1的频率f1和发射信号P的频率f0之间的差值Δf1如公式（3）所示：

由图1可知，接收探测器接受到的回波信号为发射束和接收束交汇区域（多普勒视窗）内的悬浮颗粒或气泡散射波的叠加信号，即为公式（4）中Pe所示：

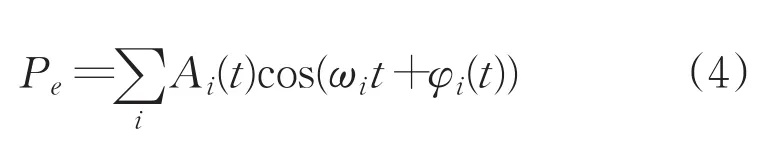
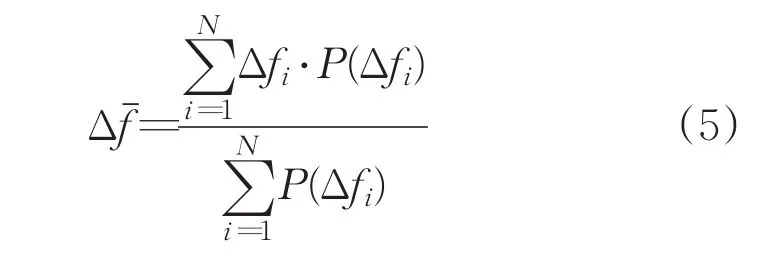
公式（5）中N为多普勒视窗内悬浮颗粒或气泡散射的回波信号数量，Δfi为第i个悬浮颗粒或气泡具有的多普勒频移，P(Δfi)为第i个悬浮颗粒或气泡形成的功率谱线强度。

由多普勒频移公式（5）可求得多普勒视窗内流体的平均速度为ˉ，具体见公式（6）：

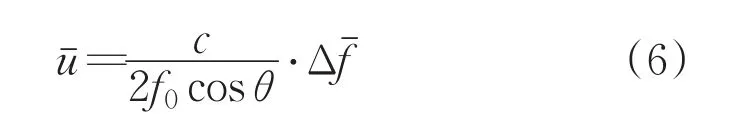
上式c为声波在水里的传播速度，随水温T的变化关系如公式（7）所示：

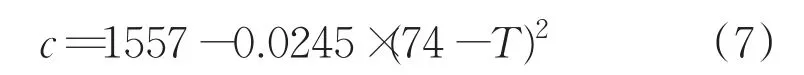
运用平凹声透镜对发射束和接收束进行汇聚，减小发散张角，使声束近似平行，缩小多普勒信息窗的体积。采用单点发射，多点接收的模式，实现多通道分区域测量。

通过上述方法测得管道内三点流速，从而确定圆形封闭管道内流体流动状态，并建立流体流速分布模型。设流体在横截面S上的流速分布函数为u(r,θ)，可求得管道流体流量表达式如公式（8）所示：

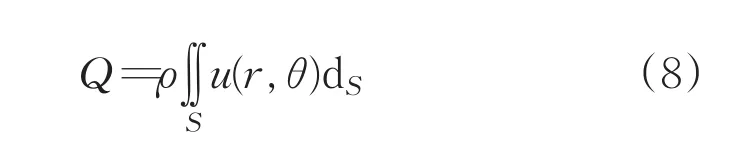
式中，ρ为流体密度，Q为单位时间内流体流过垂直截面的质量。

2 系统仿真

根据上述方法，进行封闭圆形管道流体流速测量。其中，圆形管道半径r0=0.1m，流体密度ρ=1012kg/m3，流体温度T=20oC。合理安装超声波换能器，发射端发射正弦信号。正弦信号的频率f=2.5×108HZ，幅度A=±11.5V。

在不同流速状态下，通过已接收到的回波信号，测量出r=0.04m、r=0.07m、r=0.09m处的流速，运用此方法对封闭管道内匀速流动的流体进行4次重复测量，三个探测器分别测得流体流速的数据如表1所示：

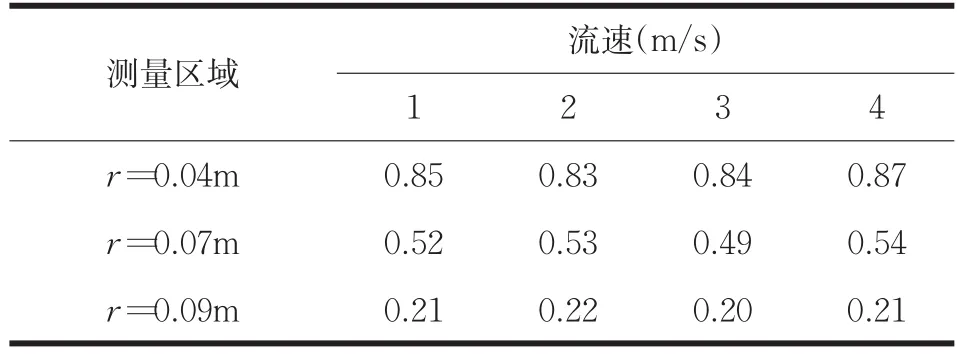
表1 封闭圆形管道内流速测量数据表

由表1可知，在r=0.04m、r=0.07m、r=0.09m处的平均流速分别为0.85m/s、0.52m/s和0.21m/s。将上述三处流体流速代入封闭圆形管道流速分布公式可解出流速系数，如公式（9）所示：

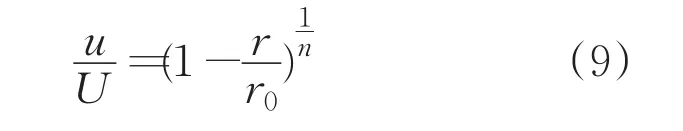
其中，U为封闭圆形管道中心流速；u为封闭圆形管道中半径为r处流体流速；r0为封闭圆形管道半径；n为流体流速系数，与封闭圆形管道内流体流速相关。

由上述所测数据可解出流速系数n=0.63，再由封闭圆形管道流体流量表达式（8）解得管道平均流速u=0.24m/s，通过标准流量表对同等环境下的封闭圆形管道内流体平均流速进行测量，其流速u=0.237m/s，上述方法可实现高精度测量封闭圆形管道流体流量。

除此之外，在不同流速下测得三组数据，其流速分布曲线如图2所示。

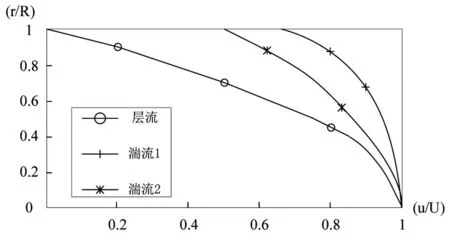
图2 流速分布曲线图

图2中的曲线描述了封闭圆形管道中不同半径r处的流体流速u的变化，在这三种不同的流速下，对其流速分布曲线系数进行计算。计算发现，测试点速度均落在速度分布曲线上，通过流体流量表达式计算出三种情况下平均流速分别为u1=0.24m/s、u2=1.20m/s、u3=2.50m/s，与标准流量表所测数据比较，极限误差均不超过0.01m/s。

3 实验系统设计与验证

3.1 实验系统设计

为了系统的测量精度，经研究设计了精度更高的超声多普勒法来实现流量的测量。系统总体由流量测量模块，DSP处理与控制系统，电源模块，按键显示模块组成，系统测量流体流量的总体设计方案如图3（a）、（b）所示。其中图（a）是测量流体流量总体设计图，图（b）是系统测量流体流量实物图。

DSP处理与控制系统是整个流量测量系统硬件电路的核心。实现对流量测量模块所测得的信号进行信号处理，本文选择TI公司推出的TMS320系列单片机，型号为TMS320F2812。

电源管理模块提供安全的电源，为整个系统的稳定工作提供了可靠的保证。

图3 测量流体流量的总体设计方案

流量测量模块主要对水管道的流体流速进行测量。其主要包括发射部分和接收部分。首先由DSP处理与控制系统产生稳定的驱动信号，在进行功率放大后驱动超声波换能器发射超声波脉冲，在管道中传播时，会遇到流体中的悬浮颗粒等杂质散射体而产生反射，反射的信号被接收探头接收后经过对信号作放大、滤波、混频等处理，最后经ADC对数据采集，然后对数据进行处理，计算出流体的流速，再根据公式（8）计算出流体流量，并通过显示模块显示。

3.2 实验验证

经研究设计的基于超声多普勒流体流量测量系统的流速测量范围为0.1m/s—20m/s，要达到测量精度为±2%。采用静态容积法来对系统所设计的流量测量系统进行试验。它的原理是在一定的时间内，根据推算标准测量容器内流体的体积，进一步计算出流体的流量。这种方法易于测得设计的系统中测量流量的精度是否能够满足要求，静态积法示意图如图4所示。

图4 静态容积法示意图

图4中，水泵的作用是将水池内的水抽到蓄水池里，当进行流量测量时，将标准测量容器的排水阀关闭，在开始进行流量测量时，开始用计时器计时的同时要将截止阀及调节阀打开，在整个流量测量过程中，要保证蓄水池是满水的状态，并且溢出的水通过排水管道排到水池里。当到达预设置的定时时间后，关闭截止阀以及调节阀，这样就完成了流量的测量。所设计的流量测量系统测得的流量值为qi；由静态容积法测得的实际标准流量值为值qsi，它是通过标准测量容器里水的体积除以试验时间计算出来的。

通过控制截止阀的打开程度来使水流速度在0.5m/s～2.5m/s范围内变化，实验数据表为表2所示。

表2 流量测试实验数据表

从表2中的实验数据可以看出此系统测量流体流量的精度满足要求。

3.3 流量实验结果的计算与分析

第i次流量测量系统检测的相对误差Ei由公式（10）得出：

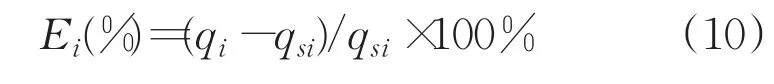
式中，qi为流量测量系统第i次测得的读数，i=1，2，3，…，n；qsi为标准测量容器第i次测得的实际流量读数。

将标准测量容器所测得的实际流量读数qsi代入表3中对流量传感器误差曲线的计算公式里，在最大误差限2%的基础上得出该流量传感器的误差曲线。而实流量测量系统测得的流量相对误差限Ei只要都在上述标准误差范围内即满足流量测量精度要求，测量方法和表3测量方法相同，表3为流量测量系统检测结果。

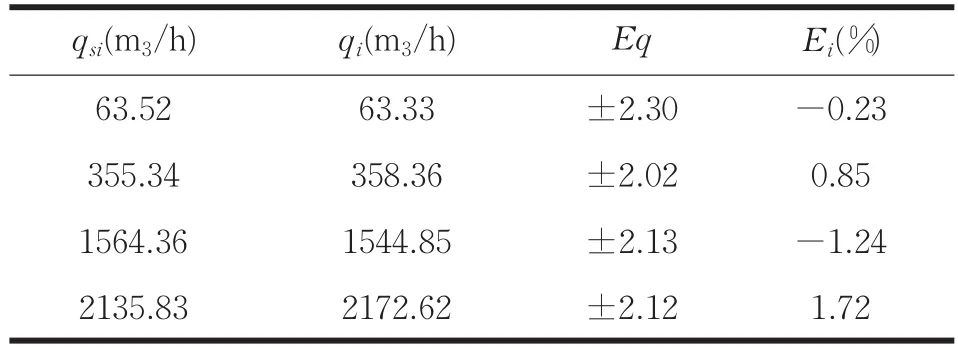
表3 流量测量系统检测结果表

从表3中的实验数据可以看出，系统的平均误差＜2%，且流量测量误差都在2级标准误差限Eq内。因此，所设计的基于超声多普勒效应的流体流量测量系统基本上满足了预期的技术指标。

4 结论

目前，中国在管道流体流量测量技术上还存在着测量精度较低的缺点，经研究，提出了一种基于多普勒法测量管道流体流量的方法[14]。该方法通过结合圆形封闭管道内流体在不同流动状态下的流速分布，将管道整个横截面的流速考虑在内，精确测量出流场中多个点的流速，从而计算出流体流量。根据上述方法进行系统仿真，从发射端发射正弦信号，在不同的流速状态下，进行4次重复测量，通过已接收到的回波信号，统计出三处不同位移处的流体流速，通过流体流量表达式计算出三种情况下的平均流速，与标准流量表比较，极限误差在合理的范围内。在此基础上设计了精度更高的基于多普勒法的实验来实现流量的测量，以便对该系统的测量结果进行分析。最后采用静态容积法来对所设计的流量测量系统进行验证[15]。通过实验的结果可以看出设计的基于多普勒法管道流体流量的测量方法基本上满足了预期的技术指标，整体方案是可行的。不仅提高了流量测量的精度，对实现多普勒法高精度测量管道流量具有重要意义，而且扩大了流量测量的应用领域。