单向电永磁作动器结构优化与动态特性分析

许宝玉 李孝坤 郝晓茹 贾言言 王坤龙

(1.河南理工大学直驱电梯产业技术研究院,焦作 454000;2.河南理工大学机械与动力工程学院,焦作 454000)

1 引 言

电磁作动器具有无接触摩擦、无需润滑、响应快等优点，广泛应用于振动主动控制、电磁悬浮以及非接触高精度定位系统等领域[1]。D.A.Weeks等人设计的适用于车辆主动悬架上的直线电磁作动器[2]，由于采用了齿轮齿条进行运动变换，降低了响应速度且反向存在冲击现象；Y-B Kim和W-G Hwang等人设计了用于车辆主动悬架上的电磁减振器，可使车辆具有良好的稳态和瞬态性能[3]；学者对螺线管作动器的结构设计方面研究较多；朱美玲等人将自行研制的电磁式作动器[4]用于转子轴承系统的振动主动控制中，使系统的振动烈度减小了50%～80%；其它还有江苏大学的串接式高能电磁作动器[5]；于锁清等人对电磁作动器进行了实验研究[6]，为其结构设计及控制策略提供了依据。以上电磁作动器均存在推力密度小，工作电流大，安匝数较大等现象。为提高电磁作动器的综合性能，本文利用磁性耦合原理，尝试将永磁体引入到电磁作动器中，提出了一种新型单向电永磁作动器，并采用有限元软件对其铁芯结构、衔铁位移及铁芯倾斜角度等进行分析研究以及对其主要参数和结构进行优化设计，验证新型电永磁作动器的可行性及其特性，为新型电永磁作动器设计及轻量化研究提供理论依据。

2 单向电永磁作动器工作原理

图1为单向电永磁作动器结构简图。主磁体2为高矫顽力的永磁材料(钕铁硼N38),镶嵌在铁芯9与磁轭3之间，极性如图中所示；材料为工业纯铁的铁芯6与磁轭固定为一体，为降低工业纯铁饱和磁感应强度，铁芯6与铁芯9留有0.3mm的气隙，励磁线圈4并列缠绕在铁芯6上；开始工作时，衔铁在重力(mg)和弹簧回复力(f)作用下保持平衡，当励磁线圈通入直流电后，铁芯6的极性如图所示，形成主磁体及磁化铁芯N极、铁芯9、衔铁1、磁轭3、主磁体及磁化铁芯S极的磁回路，衔铁在磁场吸力、自重(F1与mg矢量和)和弹簧回复力(f)共同作用下运动，通过控制励磁电流的大小可调节衔铁所受的磁场吸力；励磁线圈无电流时，主磁体绝大部分磁通量经铁芯、磁轭、主磁体S极，形成闭合磁回路，衔铁返回平衡位置。

当励磁线圈有电流激励时，忽略漏磁等因素，衔铁受到的磁场吸力为

F1=FN+μ0AN2i2/4δ2

(1)

式中：FN——永磁体对衔铁吸力，N；μ0——真空磁导率，4π×10-7H/m；A——铁芯极面积，mm2；N——线圈匝数；i——励磁电流，A；δ——气隙，mm。(图1中s为衔铁的位移，α为两铁芯接触倾斜角)。

1—衔铁；2—主磁体；3—磁轭；4—励磁线圈；5—联接螺栓；6—铁芯一；7—线圈窗口；8—不锈钢固定板；9—铁芯二图1 单向电永磁作动器结构受力图Fig.1 Force diagram of single-direction electro-permanent magnetic actuator

3 单向电永磁作动器性能参数计算

永磁材料磁性能的稳定性直接影响单向电永磁作动器工作可靠性，影响永磁体稳定性的因素主要包括温度、时效、化学、机械作用等[7～10]，其中温度对材料的稳定性影响最显著[11～13]，温度升高导致永磁体的矫顽力HC及最大磁能积BHm降低[14],见表1。

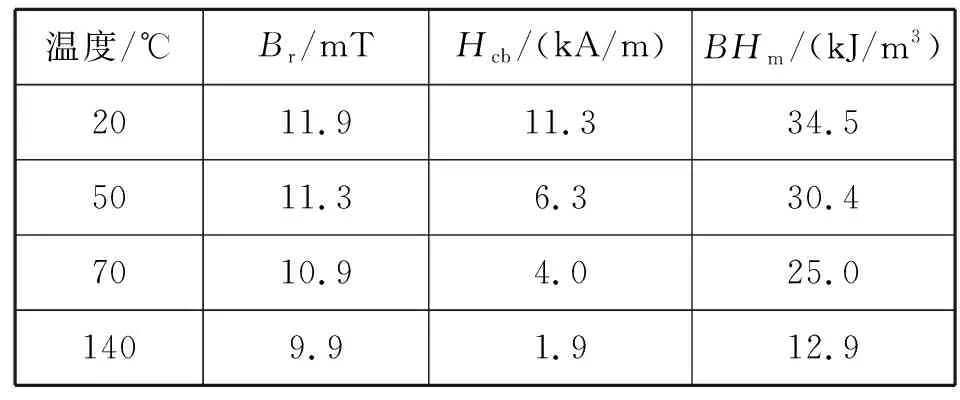
表1 不同温度下N38型NdFeB稀土永磁体的磁性能

单向电永磁作动器的永磁体磁性能受励磁线圈温升影响，为确保作动器工作可靠性，线圈温升的上限值需低于永磁体退磁温度。励磁线圈通入24V直流电后，因线圈电阻Rxq的存在使其温度上升，线圈的阻值及温升可由下式确定[15]。

(2)

(3)

式中:rx——导线的电阻率，Ω·m；N——线圈匝数；Dw——线圈外径，m；dz——铁芯柱宽度，m；qx——导线的截面积，m2；KT——线圈散热系数，(9.5～12.7)W/m2·℃；ft——线圈填充系数；bxq——线圈厚度，m；hxq——线圈高度，m；I——线圈电流，A。

线圈激磁安匝数IN可引用直流电磁铁设计公式(4)

(4)

式中：C3——磁压降系数，0.15～0.35；B0——等效气隙磁感应强度，(0.25～0.6)T；μ0——空气磁导率，4π×10-7H/m；δc——衔铁的初始行程，m。

以永磁体磁性能大幅度下降时的温度(80℃)为基准，基于上述理论公式，确定单向电永磁作动器基本参数,见表2。

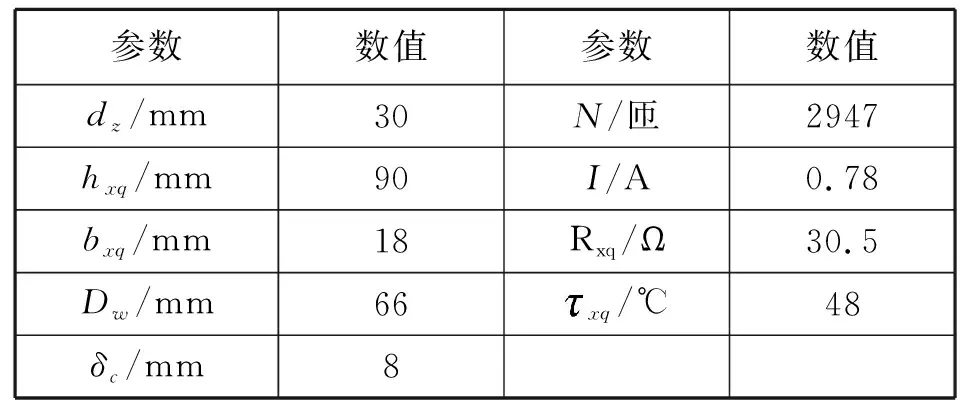
表2 单向电永磁作动器基本参数

按公式(5)计算线圈总散热功率

(5)

式中：Ps——线圈总散热功率，W；Pcd——线圈通过导热所散发热量的功率，W；Pdl——线圈通过对流所散发热量的功率，W；Pfs——线圈通过热辐射所散发热量的功率，W；S——线圈的散热面积,mm2。可认为线圈散发的热量基本正比于线圈的温升[16]，故在线圈窗口与磁轭之间预留散热通道，以降低线圈计算温升48℃使永磁体保持高磁性能。

4 单向电永磁作动器性能分析及优化

4.1 磁场分布

单向电永磁作动器选用31mm×23mm×30mm矩形状永磁体，采用四面体单元对整体结构离散，建立其二维静态磁场有限元模型，如图2所示。其中，四面体网格棱长的最大值设定为2mm，同时为保证分析结果的准确性，在单向电永磁作动器的周围建立了空气包。

图2 单向电永磁作动器有限元模型Fig.2 Finite element model of single-direction electro-permanent magnetic actuator

单向电永磁作动器两铁芯倾角α为80°且作动衔铁距铁芯1mm时，励磁线圈通入0.78A(0A)额定电流后，其磁通量分布情况如图3所示。

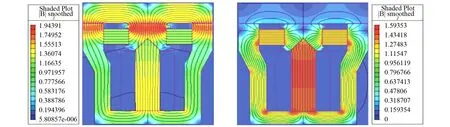
(a)两铁芯倾角为80°且线圈有激励时磁通量分布 (b)两铁芯倾角为80°且线圈无激励时磁通量分布图3 单向电永磁作动器磁通量分布矢量图Fig.3 Distribution of magnetic flux of single-direction electro-permanent magnetic actuator

由图3可见，单向电永磁作动器线圈有电流激励时，永磁体与磁化铁芯的磁通耦合成同向磁路，磁场相互叠加；无电流激励时，永磁体的磁通在作动器内部形成了封闭磁回路，有少量磁通穿过作动衔铁，对衔铁产生的电磁力仅为50N，且铁芯饱和磁感应强度低于2.158T。因线圈维持电流很小，无电流激励时，磁化铁芯相应的剩磁较小，衔铁容易释放，保证了作动器的灵敏性。

4.2 电磁力的影响因素及性能分析

电永磁作动器的电磁吸力与线圈匝数、电流及永磁体尺寸正相关，为使推力密度最大化，有必要研究两铁芯相对面的结构形式对电磁吸力的影响。图4为铁芯结构不同时，在0.78A，1mm条件下单向电永磁作动器磁感应强度矢量图。

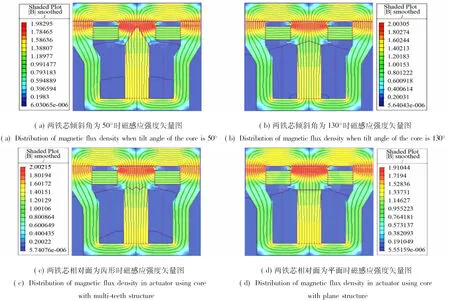
图4 铁芯结构不同时磁感应强度矢量图
Fig.4 Distribution of magnetic flux density in the actuator with different structure of iron core

图4显示，单向电永磁作动器的两铁芯倾斜角α为50°时的磁感应强度小于130°时的磁感应强度；两铁芯相对面为平面时的磁感应强度最小，铁芯为倾角的作动器磁路中的磁密优于齿形结构，且均小于铁芯饱和磁感应强度，导磁率良好。铁芯倾斜角的改变带来磁感应强度变化的同时也将会影响到电磁吸力的增减，图5为单向电永磁作动器对衔铁的电磁吸力随铁芯角度的变化曲线，图中铁芯倾斜角α(°)为横坐标，电磁吸力F(N)为纵坐标。

图5所示，铁芯的倾斜角小于50°时，随着角度增加电磁吸力变大；倾斜角大于50°时，电磁吸力随角度增加而减小；倾斜角为50°时电磁吸力达到最大值3071N。

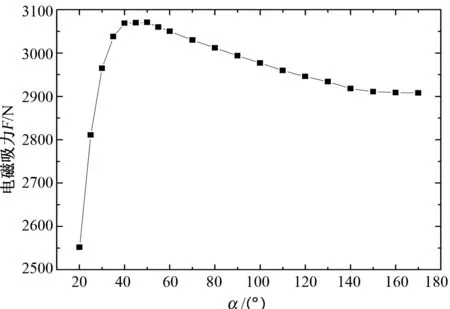
图5 电磁吸力随铁芯角度变化曲线Fig.5 Variation of electromagnetic attractive force to inclined angles of iron core

当励磁线圈通入恒定电流0.78A，作动衔铁距铁芯相对位置(位移)发生改变时，衔铁所受电磁吸力随位移变化曲线见图6所示，位移S(mm)为横坐标，电磁吸力F(N)为纵坐标。

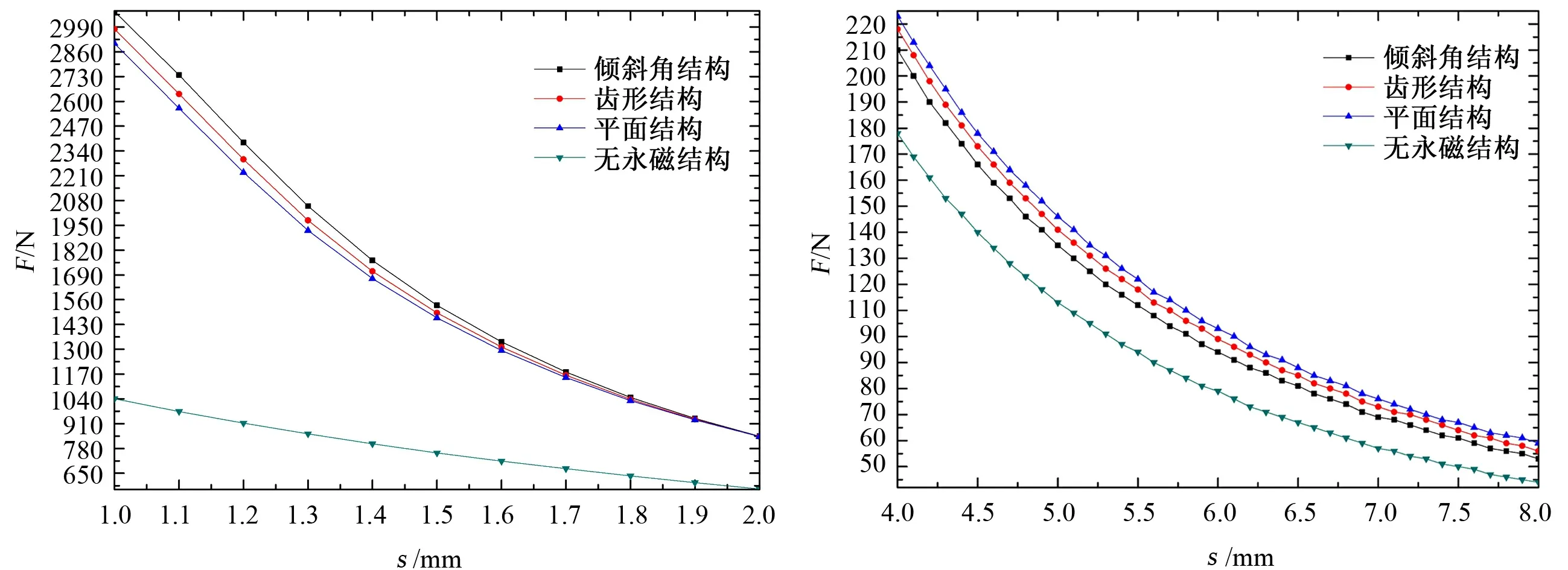
(a) 位移小于2mm电磁吸力随位移变化曲线 (b) 位移大于2mm电磁吸力随位移变化曲线图6 不同位移对应电磁吸力特性曲线Fig.6 Variation of electromagnetic attractive force to displacement of armature

从图6可以看出，铁芯结构不同的单向电永磁作动器，衔铁受到的电磁吸力随位移的增大均呈递减的趋势；衔铁在距铁芯2mm范围内动作时，两铁芯为倾斜角结构的作动器对衔铁的电磁吸力优于齿形及平面结构，且在1mm处两铁芯为倾斜角结构的作动器对衔铁产生的电磁吸力约为无永磁(传统)作动器的3倍；超出2mm时，两铁芯相对面为平面结构的作动器较两铁芯为齿形及倾斜角结构的作动器产生的电磁力大，在8mm处单向电永磁作动器较传统电磁作动器的电磁力提高了36.4%，而两铁芯为倾斜角的作动器与传统电磁作动器相比仅提高了25%。.永磁体的引入，提高了单向电磁作动器的推力密度，然而励磁线圈无电流激励时，其对衔铁也存在一定的磁吸力，图7为励磁线圈无电流激励时，单向电永磁作动器中永磁体对衔铁的吸力与位移的关系，图中横坐标表示位移s(mm)，纵坐标表示吸力F(N)。

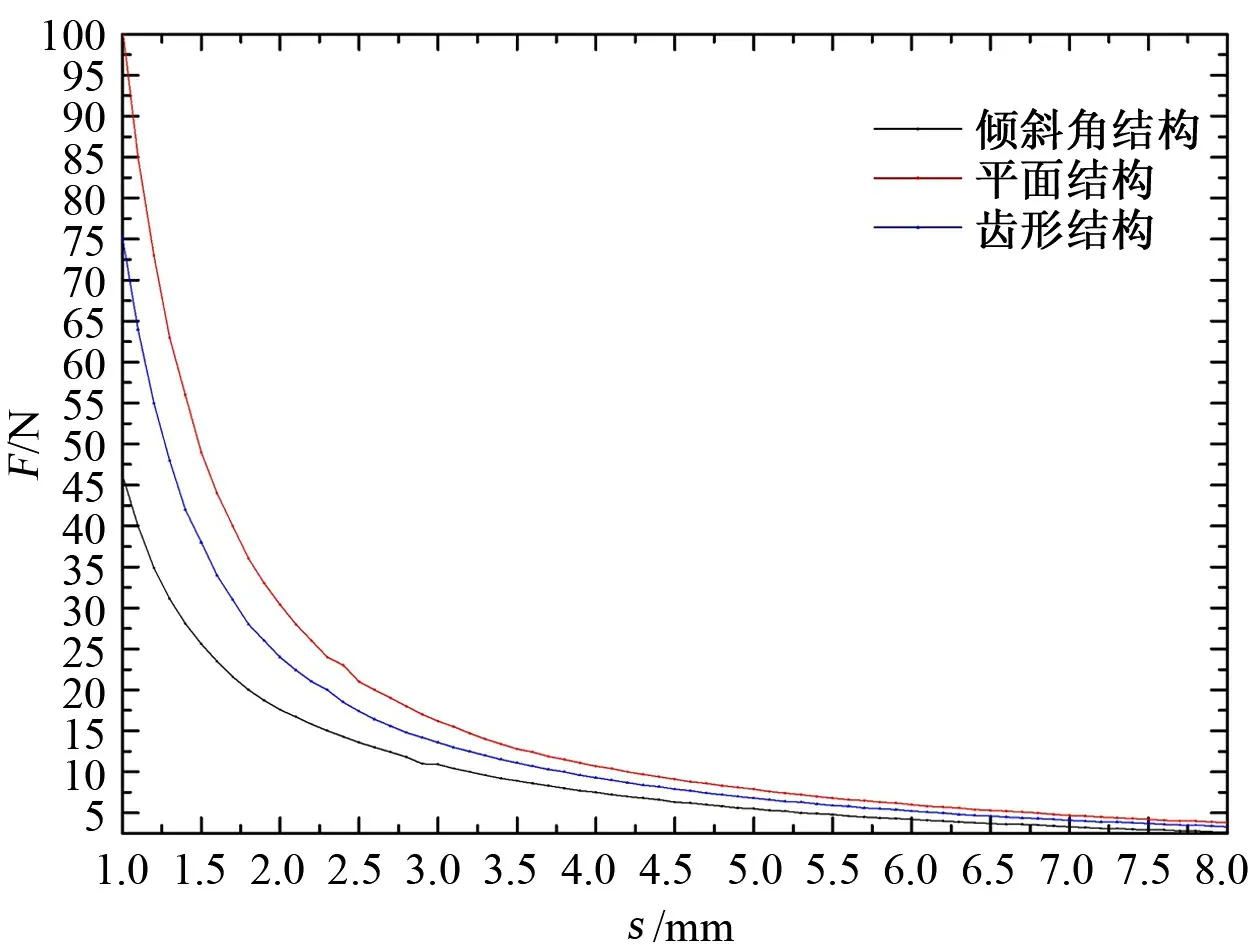
图7 吸力随衔铁位移变化曲线(线圈无电流)Fig.7 Variation of electromagnetic attractive force to displacement of armature (no coil current)

为减轻弹簧的额外负载及提高新型单向电永磁作动器的灵敏度，要求线圈无电流激励时，永磁体对衔铁的吸力越小越好，由图7分析可知，两铁芯倾斜角为50°的单向电永磁作动器的动态性能最好，两铁芯相对面为齿形结构的作动器次之，两铁芯呈平行面的作动器最差。

以上主要分析了不同铁芯结构及衔铁距铁芯相对位移对电磁吸力的影响，综合评价得出，两铁芯倾斜角为50°的新型单向电永磁作动器性能最优。在满足铁芯饱和磁感应强度及散热良好的情况下，改变励磁线圈的电流，基于非线性拟合得出作动衔铁受到的电磁吸力，以X轴代表电流I(A)的大小，Y轴代表位移s(mm)的变化情况，得出Z轴电磁吸力F(N)变化趋势，见图8。

由图8可以看出，两铁芯倾斜角为50°的单向电永磁作动器对作动衔铁的电磁吸力随着电流的变大及位移的减小而增大，反之，电磁吸力减小；在一定范围内电磁吸力与电流、电磁吸力与位移呈线性关系。电流在1.5A、位移(1～3)mm条件下，电磁吸力增加幅度较大，距铁芯距离为8mm时，电磁吸力增加幅度相对缓慢。

5 结束语

本文提出了一种新型单向电永磁作动器并对其主要参数进行了研究以及对其结构进行优化。采用有限元法分析了线圈有、无激励时电永磁作动器磁通量分布情况，表明了所设计的单向电永磁作动器工作的可靠性；通过分析对比不同铁芯结构对电磁吸力的影响，得出两铁芯呈50°倾斜角结构的单向电永磁作动器力学性能最优，且在同等条件下其对作动衔铁的电磁吸力约为无永磁作动器的3倍。随着作动衔铁位移的增加，其所受电磁吸力虽大幅度减小，但在最大位移处对衔铁的电磁吸力与单向电磁作动器相比提高了25%；此外，因永磁体的存在降低了励磁线圈的电能消耗。本文提出的单向电永磁作动器的设计理论和方法对新型大推力密度、低电流作动器的研发具有一定的理论与实际意义。