间接法测量微推力现状及关键问题分析

王大鹏 金 星 周伟静 李南雷 王 青 王健博

(1.航天工程大学激光推进及其应用国家重点实验室，北京 101416；2.西安卫星测控中心，西安 710043)

1 引 言

微小卫星具有研制周期短、质量小、发射方式灵活、成本低等优点，是未来卫星技术发展的趋势之一[1]。满足微小卫星指向与定位精度的推力通常在N～mN量级[2]。国际上已研制出多种新概念微推进器，如胶体微推进器[3]、激光烧蚀微推进器[4]、脉冲等离子体微推进器[5]、离子推进器等[6]。精确测量推力是微推进器进入工程应用的前提保证，直接影响航天器空间任务的有效完成[7]。精确测量微小推力存在不小的困难：一是推重比非常小，有时测量误差绝对值与推进器重量之比达10-7；二是易受测量环境影响，许多通常可忽略的因素，比如人的脚步或呼吸等，都可将微小的推力淹没[8,9]。

为解决测量难题，从20世纪60年代开始，国内外研究者先后研制出多种测量结构，其原理都是基于力的动力效果，将推力转换成测量台架的振动幅值或转动位移[10]。按照推进器是否与测量装置固连，可将测量方法分为直接法与间接法[11]。直接法中，推进器固连在测量台架的执行元件上，推力直接转换为测量台架的振动幅值或转动位移，典型装置有扭摆结构[12,13]、单摆结构[14]、天平结构[15]。直接法精度较高，但也存在结构复杂、易受介质供应管路及测控电缆影响、推进器及附件工作引入噪声等局限性。同时由于执行元件承重推进器，测量频率通常较低，难以辨识推进器设计者十分关注的动态推力。而在间接法中，推进器与测量台架物理隔离，可以避免供应管路及测控电缆影响，可进行装星后测量。同时，还具有可灵活选择测力方向，改变执行元件尺寸可方便调节测量频带等优点，具有广阔的应用空间。

在已有的微推力测量的综述文献中，北京理工大学刘向阳等[8]总结了2004年以前基于直接法的天平、倒摆及平行四边形结构的推力测量装置。加州理工学院James E. Polk等[16]进一步总结了2013年以前基于直接法的吊摆、倒摆及扭摆结构的测量理论，重点介绍了扭摆系统的推力、脉冲测量原理及测量装置的主要性能参数之间的关系。国防科技大学都柄晓等[11]按照直接法与间接法分类，综述了2013年以前不同测量结构的应用特点，但在间接法的综述中，只介绍了吊摆型结构的原理及特点。综合来看，目前缺少较为完备地综述间接法测量的文献。

本文将已有的基于间接法的测量装置分为吊摆型、弹性盘型、悬臂梁型三种基本动力学构型进行综述，介绍了各种测量结构中的典型结构，并对测量中理论模型、参数标定及位移测量三个关键问题进行了分析。

2 间接法测量微推力研究现状

基于间接法的测量装置中，执行元件安装在微推进器的羽流喷口处，在推进器喷射羽流的动量作用下产生动态响应。通过测量动态响应，结合预先标定出的系统参数，实现推力的测量。按照基本动力学构型来分，目前测量装置主要有吊摆、弹性盘及悬臂梁三种结构。

2.1 吊摆型结构

吊摆型结构中，目标靶通过枢轴或刀口固定，推进器与目标靶物理隔离，目标靶在推进器羽流冲击力的作用下绕固定点发生偏转，通过测量目标靶某点的位移或应力值来解算推力大小。

图1为典型枢轴连接的吊摆型结构，为英国南安普顿大学A N Grubisic等设计的微空心阴极推进器测量装置[17]。圆形目标靶(自重：398.7g，材料：钼)通过两个摩擦可忽略的枢轴固定在测量基座上，整个吊摆重心位于枢轴下方。配重位于枢轴上方，与目标靶固连在一起，用于调节吊摆重心，实现测量量程在N～mN之间变化。吊摆的位移通过激光光杠杆放大原理测量。推进器工作时，吊摆在推进器喷射冲击阶跃力的作用下绕枢轴左右摆动(动态过程)，最终稳定在初始位置右方某一平衡位置。电磁阻尼用于调节系统阻尼比，实现系统响应动态过程的调节。整个系统没有通过标定力进行直接标定，但对吊摆重心进行了精确标定。

图1 枢轴连接的吊摆结构测量原理图Fig.1 Schematic diagram of swing pendulum structure with pivot connection

若目标靶及连接装置总质量为ms，配重质量为mw，当地重力加速度为g0，偏转角为θ，吊摆重力力臂大小为Lcg，推力Fm力臂大小为Lcot(107.44mm)，则Fm可表示为

(1)

吊摆在摆动过程中，重力提供回复力，测量原理与直接法中扭摆结构相似，但不同的是，扭摆结构的回复力由枢轴提供，回复力大小与转角成正比，而吊摆结构中回复力与转角成正弦函数关系。公式(1)中Lcot在测量中是随着吊摆的位置变化的，所以解算推力时还需要进一步修正Lcot。对于氙气与氩气两种不同的工质气体，逐步增大、减小流量过程中系统响应如图2所示。由图可见，流量变化时，系统能够从一个稳态转换到另一个稳态，完成推力测量。

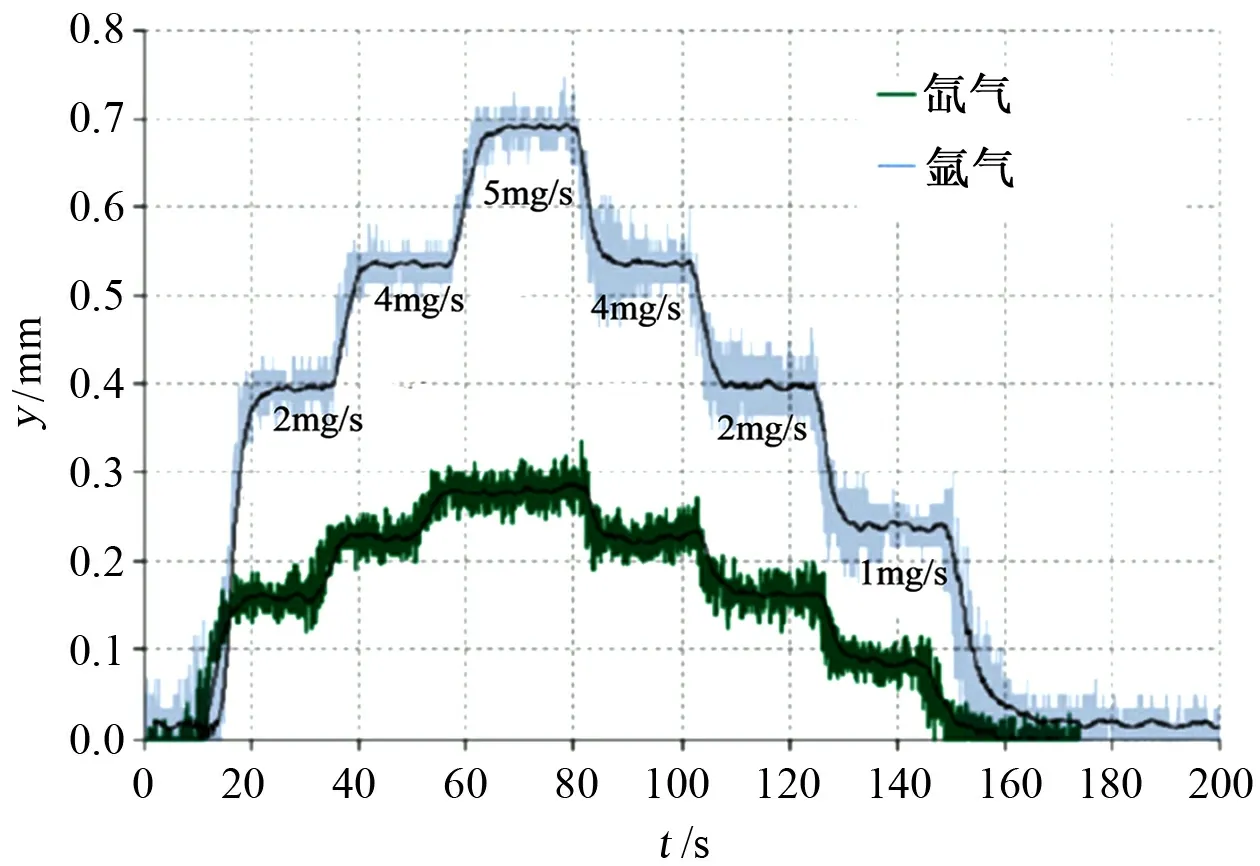
图2 不同工质，逐步增大减小流量时吊摆结构系统响应Fig.2 System responses of the swing pendulum with different propellants gradually being increased and decreased

图3为另一种典型吊摆型结构，为德国斯图加特大学Hannah Bohrk等设计的热感应式混合推进器推力测量装置[18]。该推进器结构复杂，地面测试附件较多，无法应用直接法进行测量。与图1中结构不同的是，吊摆通过刀口固定在基座上，通过与圆形目标靶(Φ1000×5，重50kg，材料铜)直接接触的应力应变传感器直接输出测量点推力，由于推力与应力应变传感器测量力臂同为d/2，因而传感器输出值即为推力大小。该测量装置量程为0～2.5N，分辨力为0.3N。在每次测量前通过砝码进行标定。

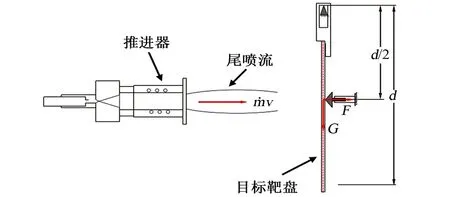
图3 刀口连接的吊摆结构测量原理图Fig.3 Principle diagram of swing structure with edge joint

对比图1与图3，图1中吊摆结构的测量量程及阻尼大小可调，精度相对更高，由于缺少阻尼元件，系统稳态误差相对较大。图3结构测量推力值较大，精度相对较低，通过传感器简化了测量结构，两者具体参数对比如表1所示。

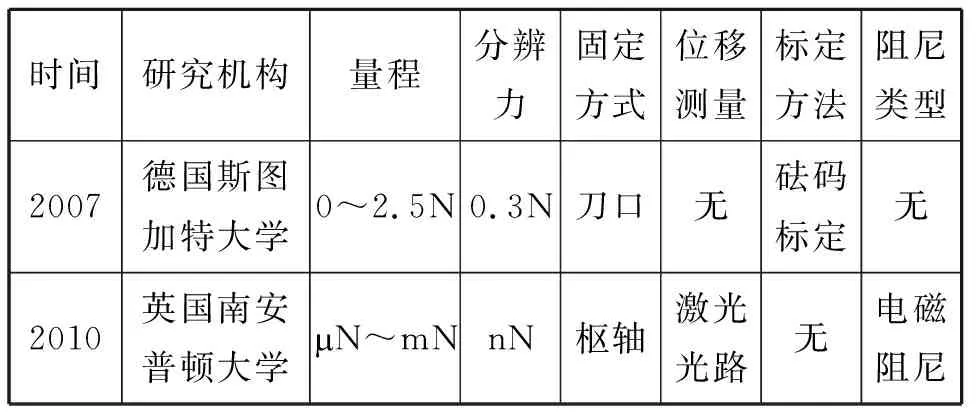
表1 两种典型吊摆结构测量装置对比

2.2 弹性盘型结构

弹性盘型结构中，质量很小的目标靶固定在弹性梁上，弹性梁两端均固定，测量推力的原理为弹性盘的形变量与推力成线性关系。

图4为2015年瑞典空间微系统实验室Subha Chakraborty研究的离子推进器测量装置[19]。目标靶盘(42mm×42mm，铝箔)粘贴在弹性支架上，弹性支架两端固定，羽流作用在目标靶盘中心，引起弹性支架弯曲振动，振动回复力由支架弹性力提供，并与位移成线性关系。达到稳态时，通过FT-S100型微传感器输出推力值。

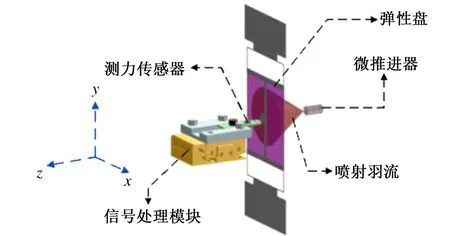
图4 弹性盘型结构推力测量原理Fig.4 Thrust measurement principle of elastic disk structure

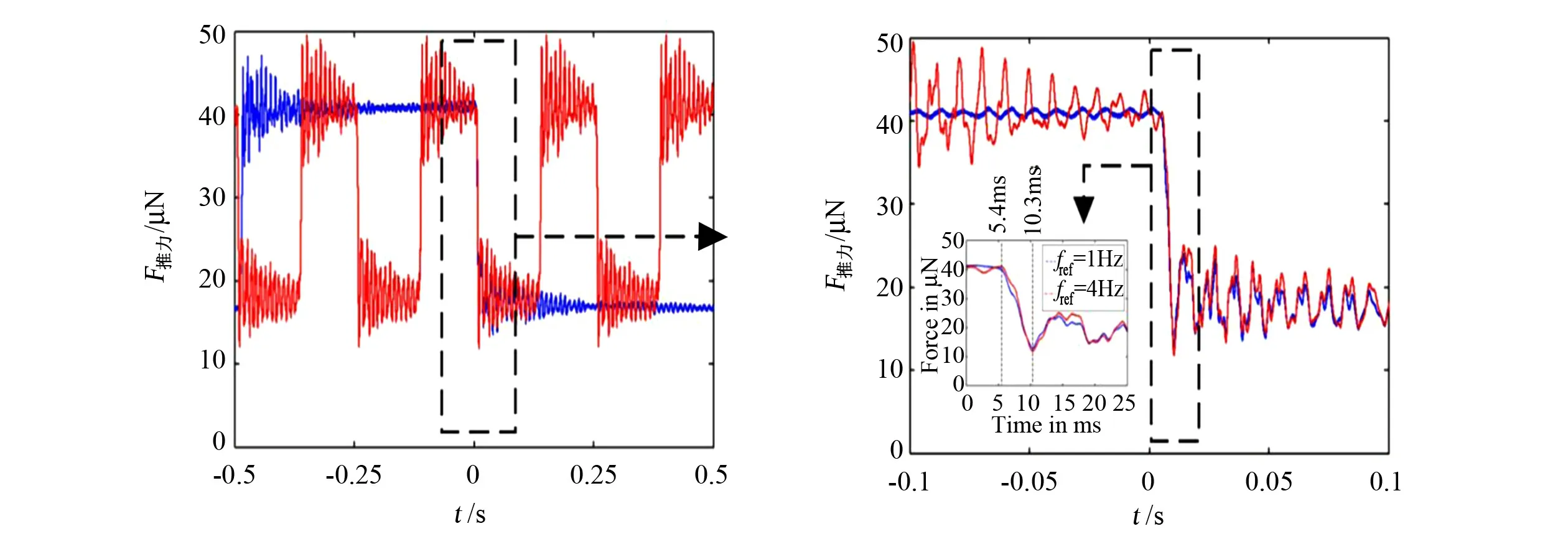
图5 弹性盘测量不同频率推力结果Fig.5 Measurement results of elastic disk under different frequency thrust

2.3 悬臂梁型结构

悬臂梁结构中，悬臂梁既作为羽流的承接元件，又作为弯曲振动元件。悬臂梁是力学中经典结构，其弯曲振动理论模型较为成熟，因而成为间接法中应用最广泛的结构。

2.3.1 测量原理

悬臂梁结构模型如图6所示，梁为等截面矩形(截面尺寸为w×h)，将推力等效为集中力载荷f，力臂大小为lf，根据悬臂梁的静力学弯曲方程，x=l处位移ν(l)表达式为

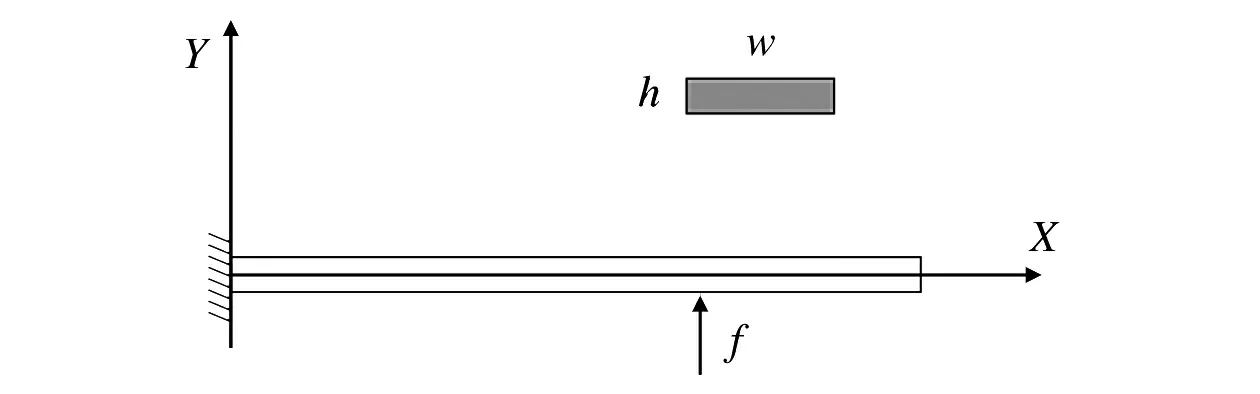
图6 悬臂梁结构模型Fig.6 Cantilever beam structure model

(2)

式中：E——杨氏模量，与材料有关;I——截面转动惯量;l——梁的长度。当lf=l时，ν(l)可表示为

(3)

由上式，lf=l时，输出恒定标定力标定出k后，测量得到推力响应的稳态位移ν(l)，即可得f大小，这是目前悬臂梁结构测量稳态推力的理论依据。

2.3.2 典型结构

早在2002年，英国南安普敦大学Paolo Gessini等人采用如图7所示的悬臂梁装置，对其设计的微空心阴极推进器进行推力测量，用以研究放电电流、放电电压、工质流量等参数与推力的关系。测量分辨力3N，量程0～0.5mN[20,21]。实验中，通过改变悬臂梁的带电极性，控制羽流中离子、分子、电子与悬臂梁之间的相互作用，可分析推力中各粒子对于推力的贡献组分，了解推进器工作物理过程。悬臂梁弹性系数采用砝码标定，采用光杠杆方法测量弯曲形变量，光斑移动距离通过位移敏感探测器(PSD)自动测量。

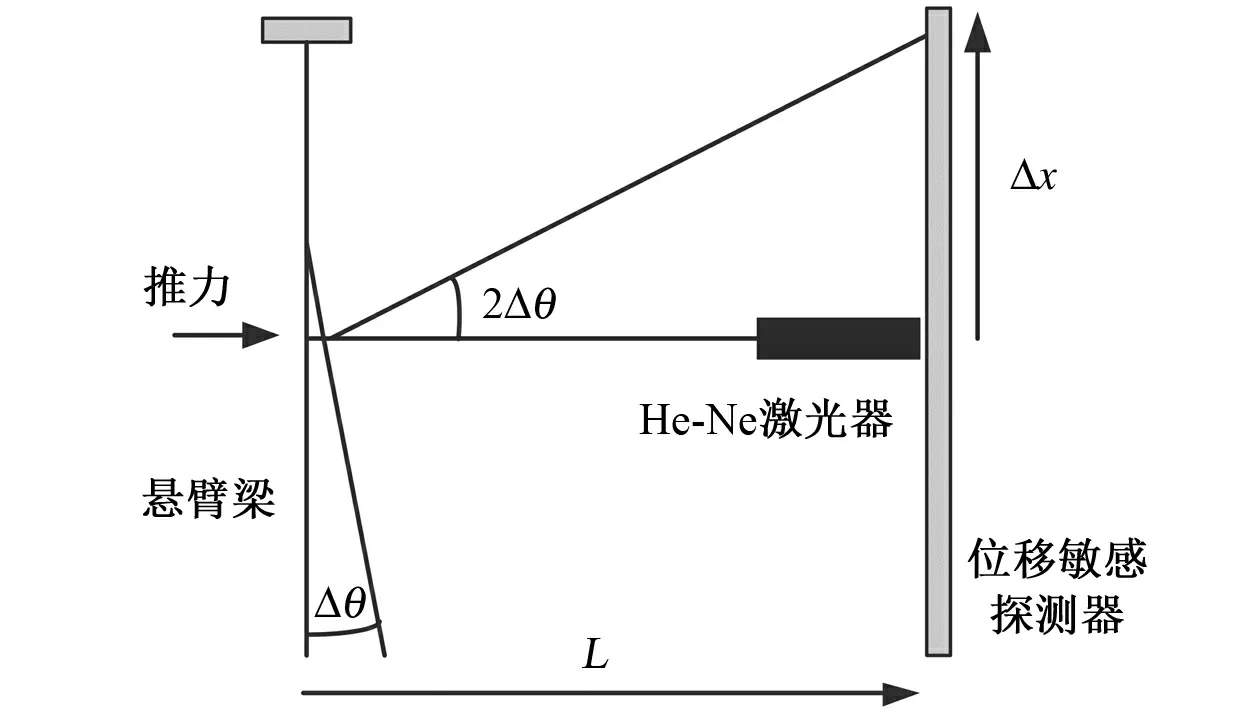
Δθ-悬臂梁偏转角;Δx-光斑移动距离;L-悬臂梁初始位置与位移敏感探测器水平距离图7 基于悬臂梁结构的微空心阴极推进器推力测量装置原理图Fig.7 Principle diagram of cantilever beam for measuring thrust of micro hollow cathode thruster

2013年，美国空军技术研究院(AFIT)需要测量Busek公司研发的胶体推进器，而重力环境下，胶体推进器只能水平放置，以保证工质均匀喷出，AFIT因而设计了一套如图8所示的悬臂梁(172.72mm×25.2mm×0.254mm)测量系统，其中系统分辨力10N，量程1N～1mN[22]。

为了在理论上更加接近欧拉-伯努利梁，AFIT在悬臂梁自由端粘贴一个铝箔做成的轻质捕获盘(重2.0g)，开机工作时，喷射羽流直接作用在捕获盘上，保证悬臂梁受力集中，将分布载荷变为集中载荷。同时，铝箔表面做粗糙处理，以使喷射粒子反射方向随机发散，尽量减小对流场影响。振动位移由激光位移传感器实时记录。悬臂梁弹性参数由砝码标定。

图8 竖直方向胶体推进器推力测量装置Fig.8 Cantilever beam structure for vertical thrust measurement of a colloid thruster

对比图7与图8，两者都是将悬臂梁视为线性弹性元件，根据推力与弯曲位移量之间的线性关系确定推力大小。图7测量水平力，而图8测量的是竖直方向的力。典型悬臂梁结构的推力测量装置如表2所示。

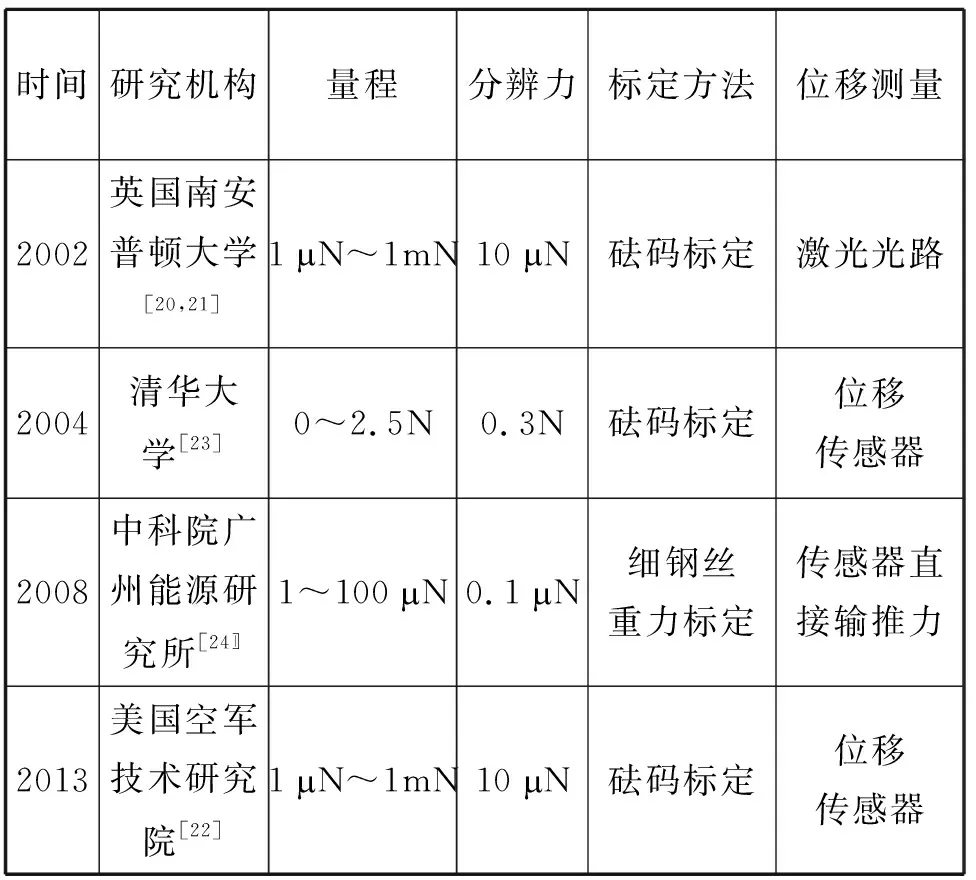
表2 典型悬臂梁结构测量装置

3 间接法测量微推力关键问题及分析

图9为推力、测量系统以及系统响应三者之间的关系，由此可以看出，推力测量的实质就是通过测量系统响应，利用实验标定得到的表示测量系统运动规律的微分方程，反向计算推力的过程。

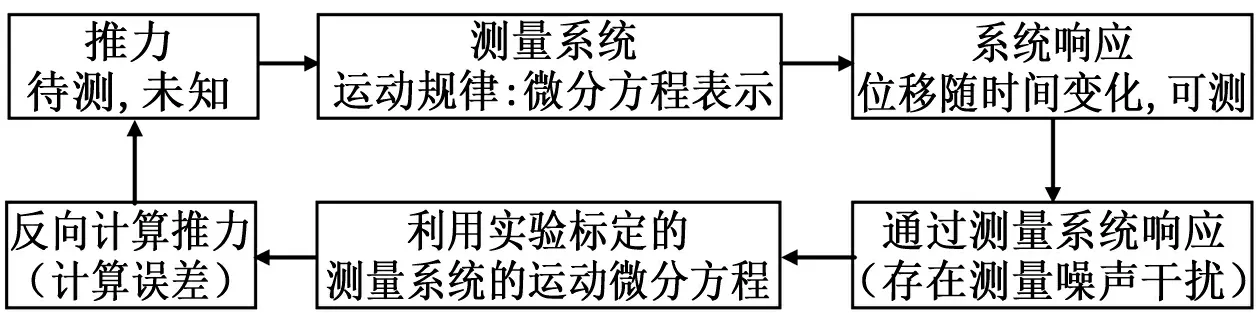
图9 推力、测量系统与系统响应的关系Fig.9 Relationship between thrust, measuring system and system response

因而，微推力测量涉及的关键问题为:

(1)推力测量理论模型：测量系统的运动规律由微分方程描述，但测量不同形式的作用力时，需要标定的参数是不同的。因而需要基于测量系统的运动微分方程，确定推力测量理论模型，确定待标定参数及推力计算方法；

(2)系统参数标定：采用实验测量方法，通过施加标定力，准确地获得反映测量系统运动规律的微分方程中的待标定参数；

(3)系统响应的测量：通常通过测量振动位移来实现，无论是系统参数标定还是推力测量，位移都是关键的直接测量量，位移的测量精度直接影响推力测量精度。

3.1 测量理论模型

目前采用间接法主要进行作用时间较长的稳态推力的测量，所依据的理论模型为稳态扭转角(位移)与推力大小呈线性关系。

吊摆型结构由重力提供回复力，在小位移振动条件下，运动方程近为二阶微分方程。相比之下，弹簧盘结构与悬臂梁结构运动方程为高阶微分方程，弯曲振动频率较高，响应速度较快，可以应用于动态推力的测量。以悬臂梁型结构为例，零初始条件下，阶跃力作用下，悬臂梁振动由无穷多个固有频率的主振动叠加。阻尼作用下，自由振动迅速衰减，最终自由端稳态弯曲量为与静态加载推力作用结果相同，梁的弯曲量与推力大小如公式(3)的线性关系。当推力作用时间较短或动态变化时，系统振幅较大，未达到稳态，此时需要基于系统动力学模型，研究系统输入输出响应特性，确定推力测量及参数标定方法。脉冲力作用下(与悬臂梁作用时间可忽略)，悬臂梁开始自由振动，由于阻尼作用，振动幅值开始衰减，根据初始最大振幅可以测量脉冲力冲量大小[25]。

由于间接法测量的是尾喷羽流的冲击力，一部分喷射粒子并没有作用在目标靶上，而且喷射粒子的反射可能会对羽流产生影响，因而间接法测量得到的推力与实际推力大小会存在一定差异[26]，这是目前限制间接法推广使用的主要因素。通过实验对比测量得到的尾喷流冲击力与真实推力是研究这一问题的可行途径。文献[27]实验结果显示通过选择合适的测量距离，冲击力与推力的测量误差在10%以内。文献[28]实验结果显示，对于30～40N推力，冲击力与推力差值在几个N水平。文献[27]、[28]直接测量推力时，都没有排除线缆干扰，可以设计体积更小的，集成在一个平板上工作的推进器样机，用以研究通过冲击力测量推力的测量误差大小。

3.2 高精度参数标定

对于吊摆型结构，主要是标定得出标定力与吊摆转角或应力传感器的输出关系。对于弹性盘与悬臂梁结构，标定的目的是得出形变量与标定力之间的线性系数。

参数标定中，高精度标定力是高精度参数标定的基础。砝码是常用的标定力产生形式，但砝码重力方向单一[24]，同时难以实现测量过程中的实时标定。电磁力[12]与静电力[29]是目前应用成熟的标定力形式，可以产生连续可调的标定力，可进行动态标定。尤其在真空实验时，可实现实时加载、卸载标定力，用以研究温度对线性系数的影响。电磁力产生装置通常由线圈与磁铁产生，静电力产生装置通常由两块通电极板产生。电磁力与静电力在使用前，本身也需要标定，通过电子分析天平进行标定是常用的方法之一。参数标定中，由于执行元件的运动，产生装置相对位置关系会发生变化，标定力输出存在一定的波动，标定时需要将此考虑在内。

3.3 高精度位移测量

位移测量中，搭建光路测量位移在结构上较为复杂，且不能直接输出位移值。目前位移传感器技术已较为成熟，直接采用激光干涉传感器及电容式传感器测量位移具有结构简单、操作方便的优点，同时传感器可直接输出数字形式的位移值，提高了测量效率。

电容位移传感器精度较高，但量程较小，激光位移传感器精度相对较低，但量程较大。推力测量中位移传感器工作环境恶劣，位移传感器需要经常标定。电容位移传感器通常是基于平行式变极距电容原理设计，工作时探头作为一个电极，被测导电对象作为另一个相对电极，测量装置执行元件的运动会导致测量对象与探头之间存在一定大小的夹角，产生极板不平行位移测量误差，因而标定传感器时也应对此进行标定。

4 结束语

间接法通过测量推进器尾喷离子作用在目标靶上的冲击力实现推进器推力的间接测量。其非接触、测量频带易于调节的特点，可以解决工程上直接法难以完成的测量难题。

(1)吊摆型、弹性盘型以及悬臂梁型结构是间接法中主要的三种结构。悬臂梁结构简单，是目前应用最广泛的测量结构。

(2)高精度标定力是高精度参数标定的基础。重力法原理简单，但存在难以完场现场标定的缺点。静电力与电磁力是应用成熟的标定力，可以完成实时标定，但使用前其本身也需要标定。位移传感器技术的成熟，简化了测量装置的位移测量。

(3)目前采用间接法主要进行作用时间较长的稳态推力的测量，所依据的理论模型为稳态扭转角(位移)与推力大小呈线性关系。弹性盘及悬臂梁为高阶振动系统，振动频率较高，响应速度快，可以用于动态推力测量，建立弹性盘及悬臂梁结构传递函数，分析动态响应过程，研究不同形式推力测量方法，是下一步的研究重点。

(4)间接法测量的是尾喷冲击力，与真实推力存在差异。需要采取合适的方法，研究真实推力与测量得到的冲击力之间关系。