多机场环境下的支线机场客流量预测*
摆倩倩 吴薇薇 陆燕楠 魏文斌 张 洁
(南京航空航天大学民航学院 南京 210016)
0 引 言
目前国内民航机场运营收入的主要来源仍为航空性业务收入,多数机场尤其欠发达地区的支线机场仍处于依靠客货吞吐量增长带动收入增长的初级发展阶段[1],客流量的大小直接影响民航机场航空性收入的多少.客流预测一直是民航业备受关注的研究领域,国内外学者对机场客流量预测的研究成果大致分为线性和非线性理论的预测方法.基于线性理论的预测方法有时间序列模型、灰色模型等[2]虽取得了较高的预测精度,但普遍存在无法反映非线性部分变化规律的问题.非线性预测方法主要有神经网络、支持向量机等,多数从机场客流历史数据本身挖掘有效信息.
近年国内支线机场建设的大发展加剧了多机场环境下邻近机场间的客流竞争态势[3],单纯的线性回归模型已经无法对复杂因素影响下的机场客流量做出准确的预测.神经网络具有较强的非线性映射能力[4],本文选取GDP、全年接待游客数量及邻近枢纽机场的旅客吞吐量为自变量[5],构造Elman神经网络与多元线性回归[6-7]的串联组合预测模型,对支线机场的客流量进行预测.以江苏地区支线机场——常州奔牛机场(以下简称常州机场)的客流预测为例验证模型的有效性.结果表明,Elman神经网络在多指标同步预测方面的稳定性较好,模型整体性能优于传统的计量经济模型,取得了较好的预测结果.
1 Elman神经网络模型
1.1 数据的预处理
本文结合《常州市国民经济和社会发展统计公报》与《南京市国民经济和社会发展统计公报》中2001—2015年的相关数据,选取常州市GDP(x1)、常州市全年接待游客数量(x2)、南京禄口机场旅客吞吐量(x3)为自变量对常州机场旅客吞吐量(y)进行预测[8].
(1)
(2)
1.2 指标相关性及显著性分析
运用SPSS进行相关性分析,结果见表2.
由表2可知,各指标与因变量间的相关系数均大于90%,存在显著的相关关系.
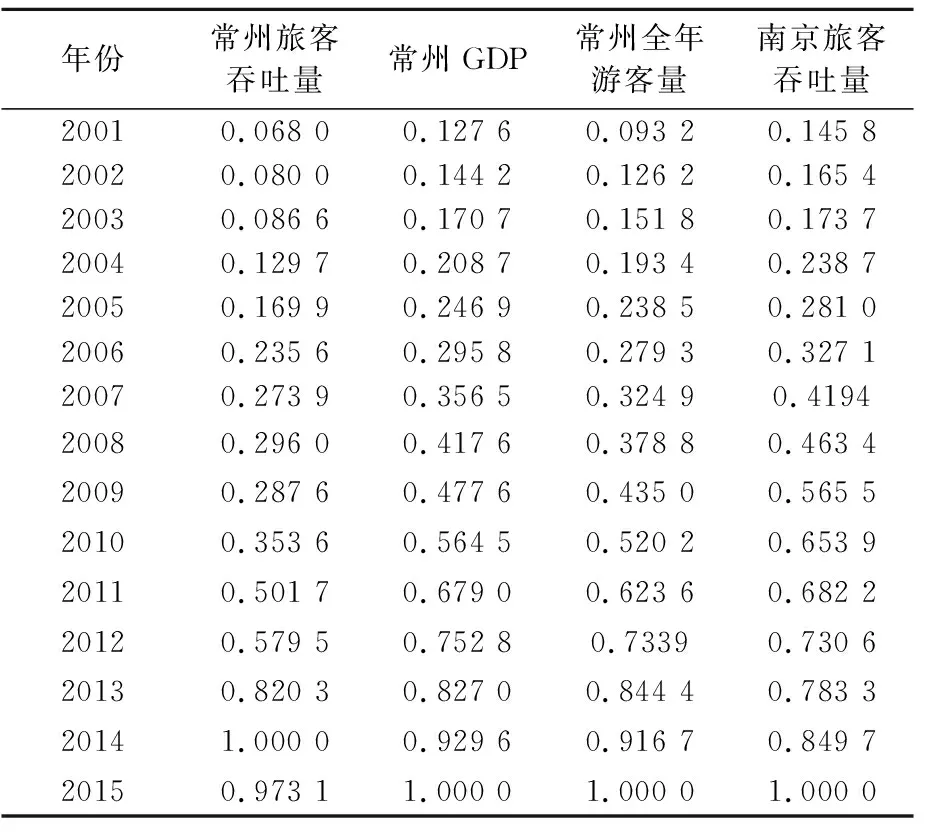
表1 常州机场旅客吞吐量及相关指标的历史数据
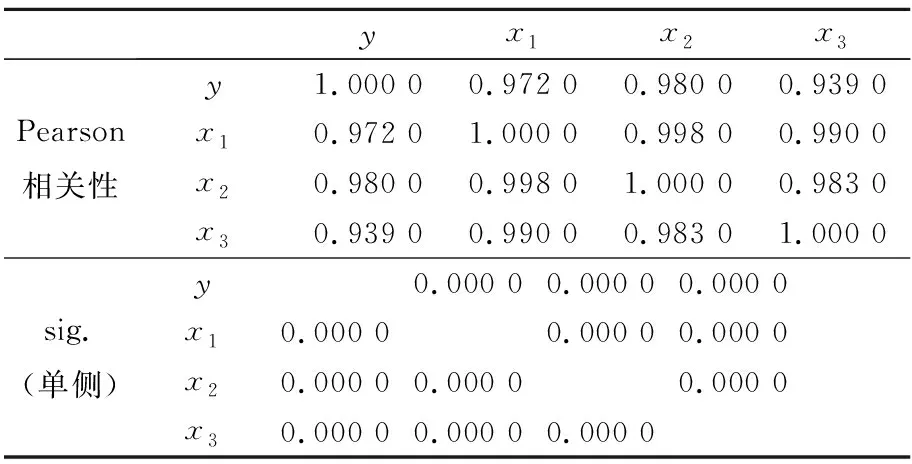
表2 指标相关性分析
1.3 Elman神经网络模型结构及原理
1.3.1Elman神经网络的结构
Elman神经网络是一种具有局部记忆和局部反馈连接功能的递归神经网络,通过在BP神经网络基本结构的基础上加入一个承接层,将隐含层的输出进行延迟与存储,并自联到隐含层的输入.这种自联方式在增强网络对历史数据敏感性的同时更好的实现了数据的动态映射,适用于时间序列问题的动态建模.
设网络的输入层包含r个节点,隐含层和承接层均包含n个节点,输出层包含m个节点.则输入向量I(k)∈Rr,输出向量O(k)∈Rm,隐含层输出向量x(k)∈Rn*n,承接层输出向量xc(k)∈Rn*n.f,g分别为输出层、隐含层的传递函数.
网络的数学模型为
xk=f(wCxc(k)+wHI(k-1))
(3)
xc(k)=x(k-1)
(4)
o(k)=g(wOx(k))
(5)
式中:wH,wC,wO分别为输入层与隐含层、隐含层与承接层、隐含层与输出层之间的连接权阵,wH∈Rn×r,wC∈Rn×n,wO∈Rn×m.
1.3.2Elman神经网络权值修正的学习算法
设训练集为(I(k),Od(k)),网络实际输出为{O(k)},k=1,2,…,N.其中:
I(k)={I1(k),I2(k),…,Ir(k)}T,Od(k)=
{Od1(k),Od2(k),…,Odm(k)}T,O(k)=
{O1(k),O2(k),…,Om(k)}T
设网络各层神经元的输入输出分别为μ、O,如隐含层第i个神经元在k时刻的输入、输出分别为μi(k),Oi(k);输出层第j个神经元的输入、输出分别为μj(k),Oj(k).
Oi(k)=g(μi(k))
(6)
Oj(k)=f(μj(k))
(7)
由于动态递归网络的输出与当前及过去时刻的输入信号均有关,因而必须采用动态学习规则.本文对递归网络学习算法的研究采用有序链式法则.
令ej(k)为第j个输出节点在k时刻期望输出与实际输出值之间的误差,即
ej(k)=Odj(k)-Oj(k)
(8)
定义k时刻网络权值调整的误差函数为
(9)
修正后的权值计算公式为
w(k+1)=Δw(k)+w(k)
(10)
下面以隐含层与输出层的之间的权值调整为例,分析逐层反向调整网络权值的具体步骤:
(11)
根据微分链式法则
-ej(k)f′(μj(k))Oi(k)
(12)
权值修正量为
(13)
引入局部梯度的定义
ej(k)f′(μj(k))
(14)
则式(13)更新为
(15)
采用上述有序链式法则对图1中的权值进行调整.
(16)
同理,隐含层的权值为
(17)
关联层的权值为
(18)
2 指标预测的Elman神经网络模型
2.1 Elman神经网络模型的指标预测步骤
1) Elman神经网络预测的样本数据划分 以常州机场2001-2013年(下文分别以1~13表示)的指标数据为基础,构造训练样本矩阵:
pk=(x1k,x2k,x3k),k=1,2…,13
(19)
式中:k为指标数据取自的年份.
令P1=p1:p4,P2=p2:p5,…,P10=p10:p13则训练样本矩阵T为
T=[P1,P2…,P10]=
(20)
以P1为例:p1:p3为模型输入,p4为模型的目标输出,依此类推,相当于一个时间序列问题,可以通过Elman神经网络进行预测.其映射函数表示为
pk=f(pk-1,pk-2,pk-3),k=4,5…,13
(21)
2) 神经网络的参数设置 反复训练并不断调整神经网络的参数设置,对比发现,当隐含层节点数为9,学习速率为0.05,最大训练次数为10 000时,网络的预测误差最小且预测性能稳定.
2.2 指标预测结果分析
Elman神经网络测试样本输出数据反归一化处理后的结果见表3,预测误差率图见图1.
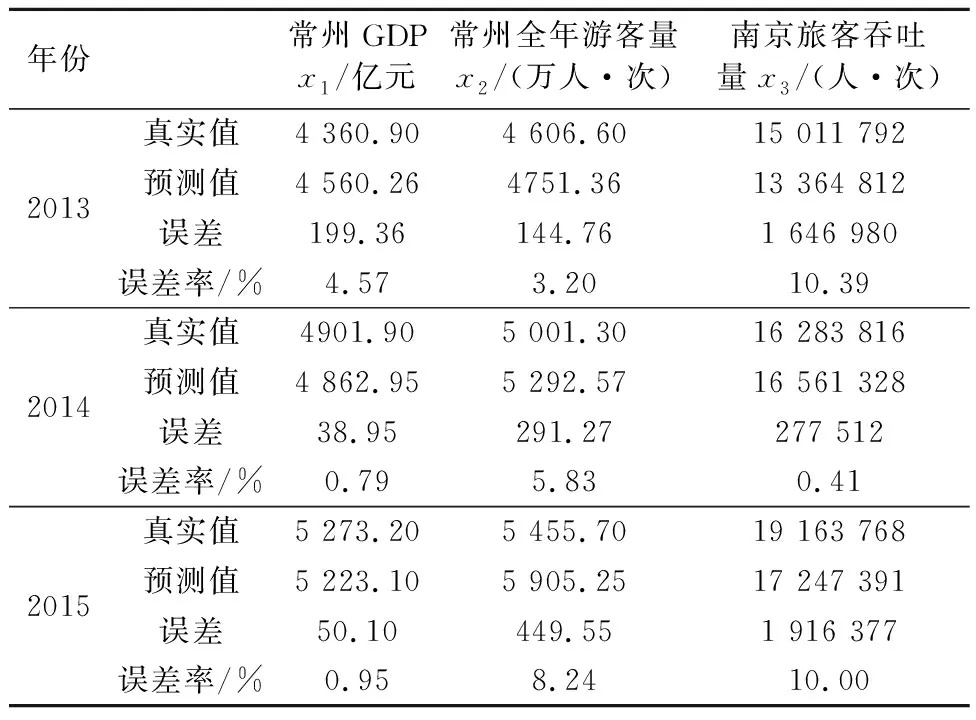
表3 Elman神经网络测试样本指标输出结果
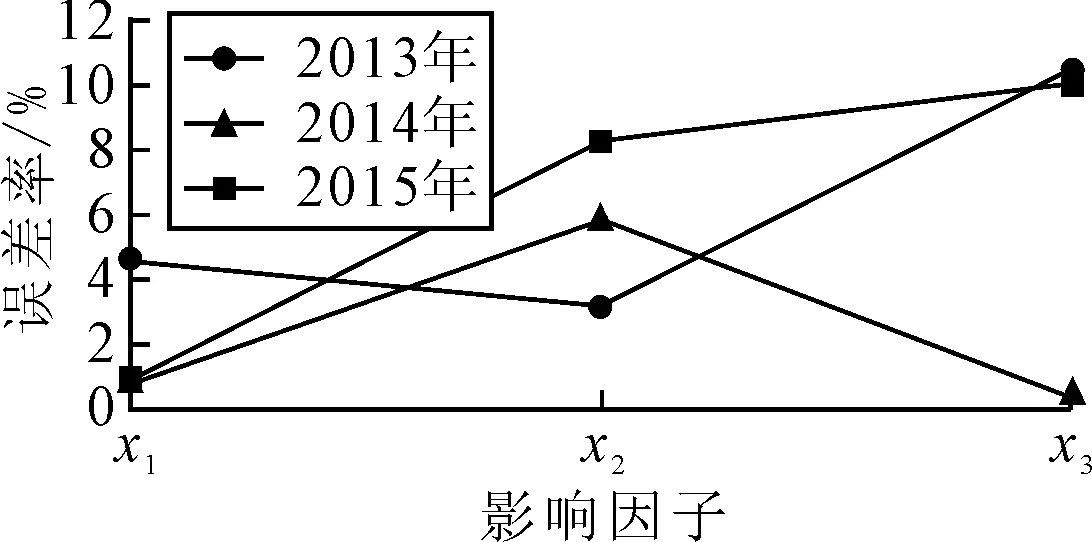
图1 Elman神经网络预测误差率图
由于支线机场客流量大小还受到外来流动人口数量、旅客出行时间成本、地面交通可达性等随地区经济、发展现状等快速变化且不易量化因素的影响,本文仅选取近三年的客流量数据进行模型验证.验证结果显示,模型对13,14,15年指标预测值的平均误差率分别为1.53%,3%,7.5%,虽呈现一定的误差累积趋势,但仍小于10%,说明该神经网络对多指标预测的效果较好.模型训练过程的误差下降曲线见图2.
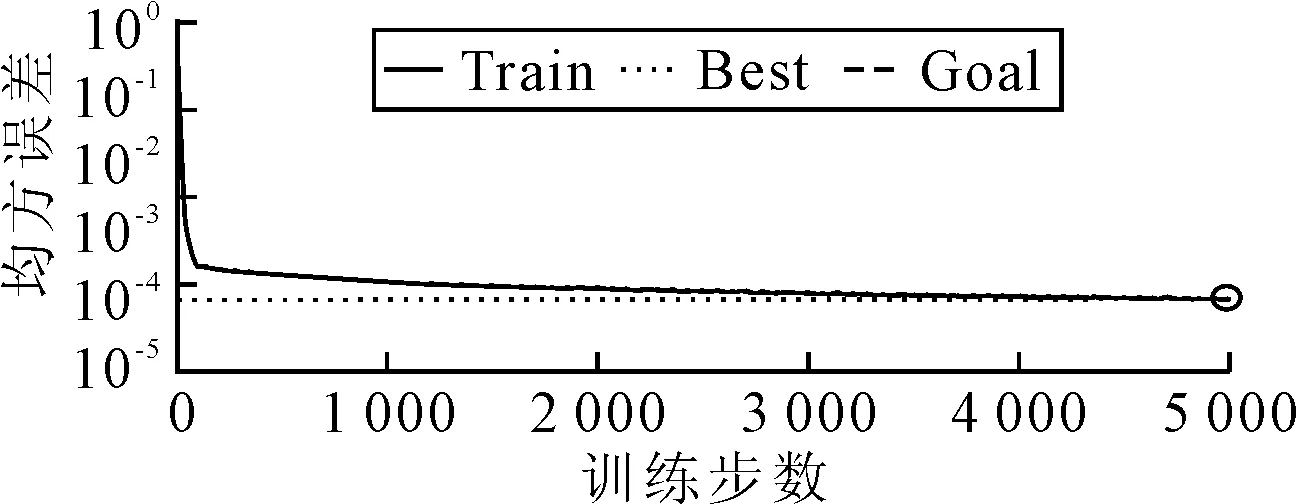
图2 Elman神经网络训练误差下降曲线图
用训练好的网络对2016-2018年指标值进行预测,结果见表4.

表4 Elman神经网络指标预测结果
3 基于多元线性回归的客流量预测
3.1 构建客流量预测的多元线性回归模型
本节仍以表1所示历史数据为基础,常州机场年旅客吞吐量作为被解释变量,常州GDP、常州全年游客量、南京机场旅客吞吐量作为解释变量,构建多元线性回归模型,表达式为
(22)
式中:k=1,2,…,12;α0,α1,α2,α3为模型中各影响因素的回归系数.
运用Matlab对上述指标数据进行多元线性回归分析,结果见表5.
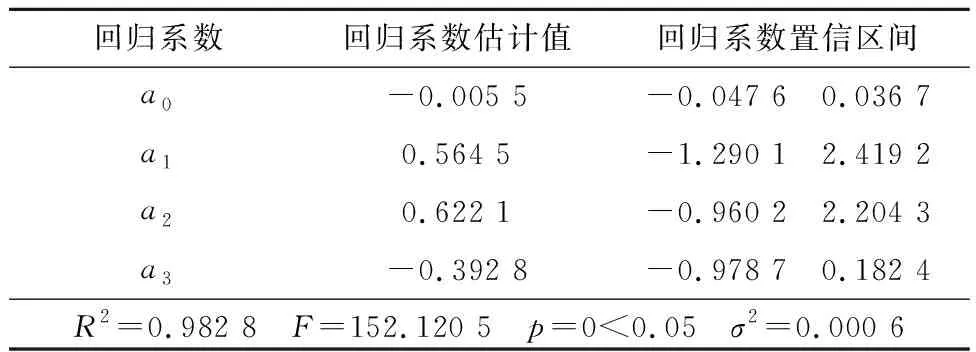
表5 回归模型系数、系数置信区间与统计量
由图3可知,样本残差均匀分布在合理的区间范围内,未出现异常的数据观测点.R2=0.982 8,接近于1,表明模型拟合程度较好.F=152.120 5,p=0<0.05,说明模型的线性关系在95%的置信水平下显著成立.

图3 残差杠杆图
回归模型为
y=-0.005 5+0.564 5x1+
0.622 1x2-0.392 8x3
(23)
3.2 模型预测结果的对比分析
分别将2013—2015年的指标实际值与Elman神经网络输出的指标预测值带入式(23),对常州机场客流量进行预测并将结果反归一化处理,分析比较不同模型的预测精度,结果见表6.
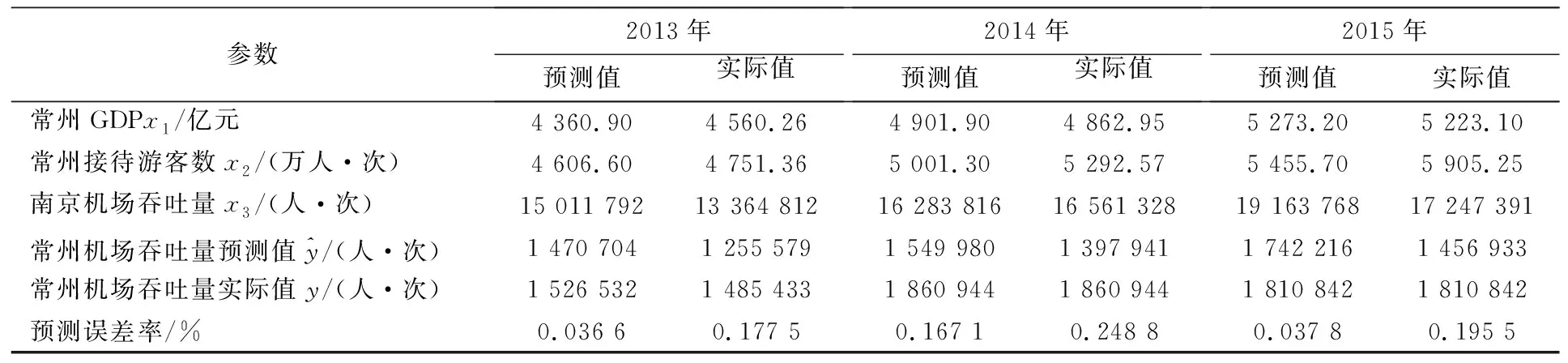
表6 常州机场旅客吞吐量预测结果对比
由表6可知,单纯的多元线性回归模型预测误差率均大于15%,结合Elman神经网络指标预测的多元线性回归模型的平均误差率为8%.其中2014年的预测误差明显大于其他年份.
2014年南京机场启用T2航站楼,与新航站楼配套的停车场、地铁机场线、长途大巴等公共交通设施齐全,大大提高了机场的服务能力.数据显示,2015年南京禄口机场旅客增量为往年的3倍,可视为指标数据增长的异常值,导致常州机场2014年的吞吐量预测结果出现较大误差,符合实际情况.
3.3 常州机场的客流量预测
对常州机场2016-2018年的旅客吞吐量预测结果见表7.
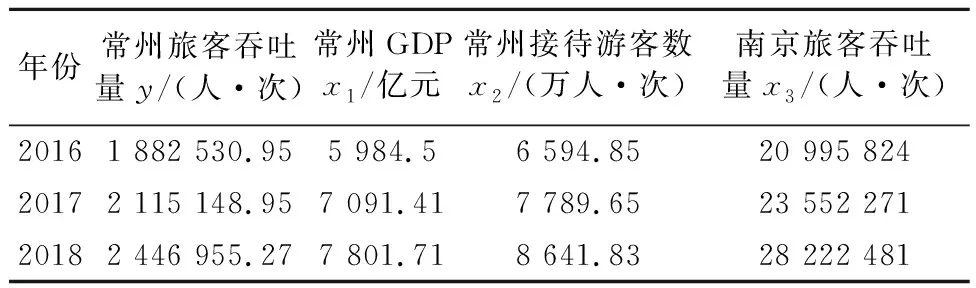
表7 常州机场2016-2018年旅客吞吐量预测结果
4 结 束 语
Elman神经网络因结构中包含特殊的延时算子而具备记忆隐含层神经元前一时刻输出值的特性.模型通过修正前馈连接部分的连接权矫正并提高了预测精度,凭借神经网络良好的学习能力实现了多个指标的同步预测,避免了传统指标预测方法造成的误差累积,在此基础上结合多元线性回归模型取得了误差相对较小的预测结果;然而目前的研究成果仍存在缺点和不足:由于部分指标数据的获取受到限制,本文仅考虑邻近机场对客流的竞争,而地面交通(尤其高铁)亦对民航旅客存在明显的分流作用,对于民航与地面交通运输方式间的客流竞争关系,有待进一步研究.

