基于声发射技术的砂轮磨损实验研究*

王洪雨，姚振强，许 胜

(上海交通大学 机械与动力工程学院，上海 200240)

0 引言

磨削加工中，砂轮磨损状态决定磨削性能，影响磨削加工质量和效率。砂轮磨损严重，将造成磨削力显著增大、工件磨削烧伤，使表面质量恶化。为保证加工质量，通常在砂轮还没有达到工作寿命极限时，定期对砂轮进行修整,具有局限性和盲目性。而声发射是一种可以对缺陷的现状以及发生历史进行监测的无损检测手段[1]，其应用领域广泛，适用于金属加工中工具磨损的检测[2]。声发射(acoustic emission，AE)是材料局部能量快速释放产生的弹性波[3]。声发射信号分为连续型、突发型以及混合型三类[4]。本文利用能量法与特征值方法结合对声发射信号进行分析。近年来，国内外多位学者对砂轮磨削中声发射信号进行监测，并对信号进行适当的处理变化，以对砂轮磨损状态进行表征。Inasakia[5]利用声发射技术监测陶瓷结合剂刚玉砂轮磨削轴承合金的过程，将声发射信号的幅值和频率变化作为特征值，用以表征砂轮是否磨损。A Hassui等[6]使用振动传感器与声发射传感器，监测磨削过程，认为10kHz以上的声发射RMS信号和100Hz以上的振动信号相结合，可以用来预测砂轮寿命，决定砂轮是否磨损，但实验系统复杂。B Karpuschewski等[7]利用声发射信号和功率信号作为磨削过程的监测量，提出一种磨削过程在线监测系统，用来监测砂轮磨损状态，但多种信号采集使分析变得困难。国内学者王晓强[8-9]对刀具磨损信号进行多元采集，但采集和分析过程较为复杂。刘贵杰等[10]提出一种通过利用声发射(AE)传感器探头与磨削表面摩擦产生的AE信号中提取有关磨削表面粗糙度信息量的方法，来监测磨削表面粗糙度，判断砂轮磨损状态。杨振生[11]利用声发射传感器监测磨削过程，并利用希尔伯特变换对声发射信号进行特征提取，表征砂轮磨损。石建等[12]利用小波分析方法，对声发射信号进行小波分解，研究了小波分解系数与砂轮磨损的对应关系，但数据采集量大，花费时间长。杨杨[13]利用声发射监测电镀金刚石磨削复合材料过程，并利用小波分析方法对声发射信号进行特征值提取，作为砂轮磨损的特征量。本文在前人对砂轮磨损的大量研究之上，针对其方法的不足，多次实验研究提出一种新的砂轮磨损过程特征值提取方法。该方法信号采集方便，计算简单，通过监测磨削过程中的声发射RMS信号，进行傅里叶变换，利用声发射频域信号频谱矩心特征值并结合工件表面粗糙度表征砂轮磨损状态，得出砂轮磨损过程的周期性规律，并在显微镜下观察砂轮磨损状态，进行实验验证。

1 实验设备

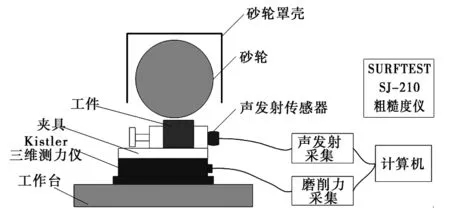
图1 实验系统组成

该实验在德国PROFIMAT MT 408 高速精密平面磨床上进行，实验系统见图1，包括平面磨床、Kistler三维测力仪、夹具、工件、声发射传感器、声发射以及磨削力采集装置(电荷放大器以及前置放大器)、SURFTESTSJ-210粗糙度仪、计算机等组成。这套系统的特点在于拥有高速大容量的信息储存功能，声发射信号在采样频率1MHz的情况下可以连续采集30s。此外，声发射传感器采集装置包含硬件滤波装置AE-Piezotron-coupler-5125，截止频率为100kHz～900kHz，可以有效滤除干扰信号。实验为快速获取砂轮磨损的声发射信号，选用的实验参数见表1。

表1 实验参数

2 信号采集结果

2.1 单次磨削过程的声发射RMS信号

根据图2可知，磨削过程中的声发射RMS信号幅值在0.4mV～1.0mV之间，切入阶段和切出阶段声发射信号RMS幅值均比稳定磨削过程中大，并且切入段的持续时间比切出持续时间略长。

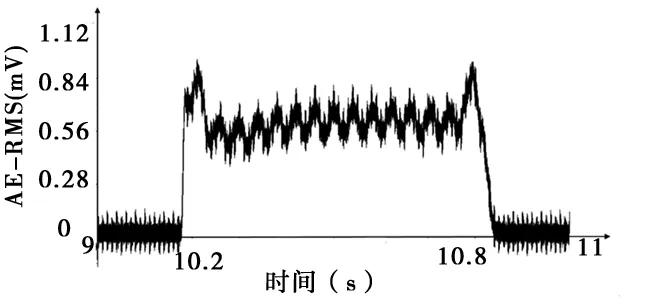
图2 单次磨削声发射RMS信号

2.2 连续磨削的声发射

为了使砂轮从修整结束初期快速进入砂轮磨损阶段，采用上述固定磨削工艺参数，连续磨削，采集磨削过程中的声发射RMS信号以及磨削力信号，并测量工件表面粗糙度，直至砂轮进入剧烈磨损阶段，共进行180刀磨削，采集结果如下：

如图3显示，在磨削开始时，砂轮切入工件和切出工件的声发射RMS信号幅值明显大于砂轮稳定磨削中的声发射RMS信号，并且切入阶段的声发射RMS信号幅值大于切出阶段的声发射RMS信号。图4显示，随着磨削过程的进行，砂轮磨损的加剧，声发射RMS信号幅值逐步增大，且趋于稳定，切入阶段的声发射RMS信号幅值始终高于切出阶段的声发射RMS信号。从图3和图4中看出，在整个磨削过程中，声发射RMS信号幅值始终保持在0.4mV～1.0mV之间，这也说明从声发射信号时域信息中无法找到合适的表征砂轮磨损的特征值。

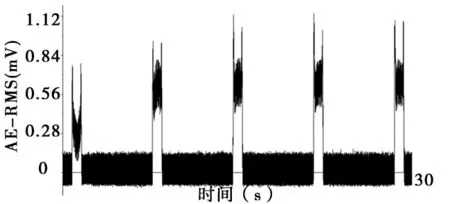
图3 第21～25次磨削声发射信号

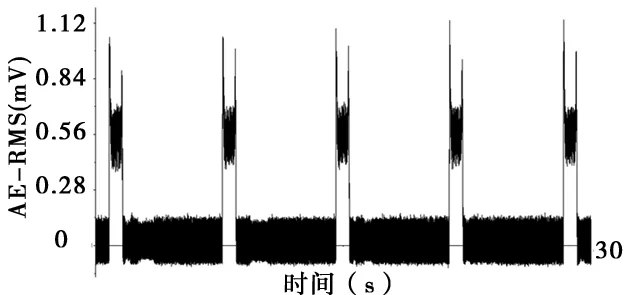
图4 第175～180次磨削声发射信号

磨削力的采集是为了鉴定砂轮的磨损状态，砂轮磨损初期，磨粒比较锋利，磨削力较小，图5显示，在砂轮工作初期，磨削力约为325N，并且在稳定磨削过程中，磨削力维持在325N左右。随着磨削过程的进行，磨粒产生钝化，磨削力开始增大，砂轮继续磨损，磨削力明显增大，如图6所示，约为450N，磨削力增大了39%。为了准确鉴定砂轮磨损状态，在放大100倍的显微镜下，观察磨粒状态如下图所示。从图7中可以明显的看到锋利的磨刃，并且磨粒之间存在较大的孔隙。图8中磨粒磨损严重，并且磨粒之间发生严重的堵塞。

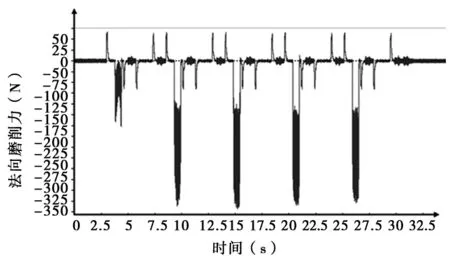
图5 第21～25次磨削法向磨削力

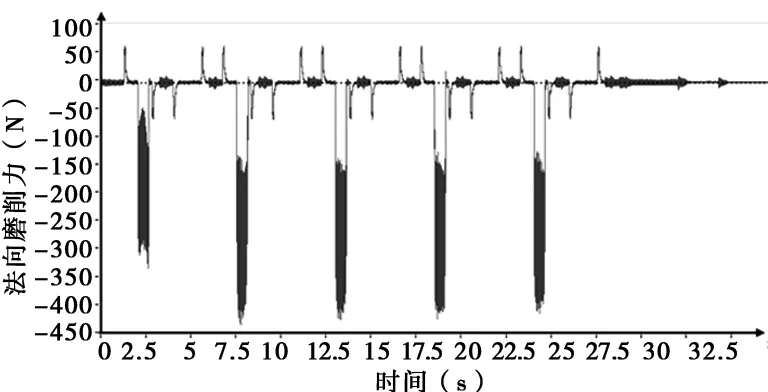
图6 第175～180次磨削法向磨削力

图7 砂轮磨损初期形貌 图8 砂轮磨损后期形貌

3 信号分析

3.1 小波分解与重构法去噪

小波分解是将信号分解为频率较低的近似系数以及频率较高的细节系数。

小波是一种持续时间非常短暂的震荡波，小波分析具有很强的时频分析能力，可以有效地对材料内部的缺陷进行检测，能够对隐藏的瞬变信息和短时事件进行识别[14]。

为进行小波分析，需要寻找具有一定特性的函数ψ(t)，此函数成为小波基函数。基函数具有如下特点：

(1)

它的傅里叶变换满足接受条件：

(2)

一旦小波基选定，它的连续小波变换定义为：

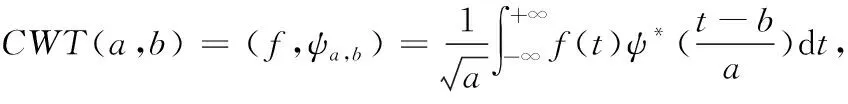
(3)

式中，a为尺度因子，可以对小波基进行拉伸和缩放；b为时间因子。

根据傅里叶变换的性质，时间因子b只是改变信号在频域的相位，而尺度因子a则对信号起着频限的作用，信号被分成不同的频率成分，尺度因子越大，频率越小，频带越宽。因此可以利用该性质对信号进行分解。小波分解的原理图如图9所示。

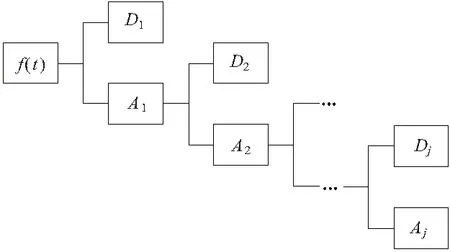
图9 小波分解原理图

其中，A表示信号的低频部分，D表示信号的高频部分。对信号f(t)进行j尺度的小波分解结果可以用以下函数表示：

小波去噪方法有多种，包括重构法去噪、阈值去噪法、平移法去噪以及极大值法去噪[15]，针对此次实验采集的砂轮磨损声发射信号，本文利用Daubechies小波基对声发射RMS信号进行5层分解，利用能量法对各层小波系数的能量进行分析，得出砂轮磨损过程中小波系数能量的变化规律，并将小波分解结构中能量比较低的信号成分滤除，利用小波重构的方法对原始信号进行重新合成，从而滤除原始小波中能量较低的噪音和振动等干扰信号，达到重构法去噪的目的。以采集信号中的其中一组信号进行示例分析，小波分解结果如图10所示，每层系数能量显示结果为图11。

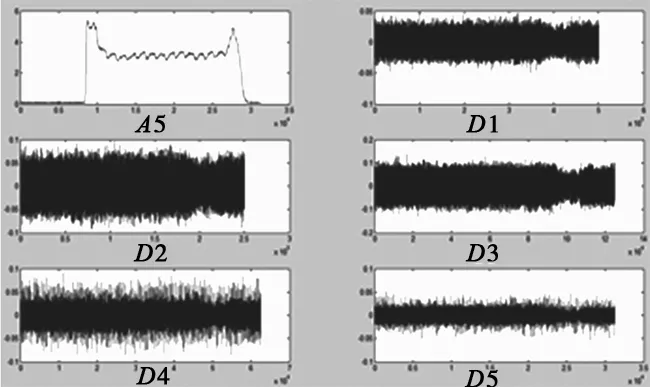
图10 声发射RMS信号小波5层分解结果图

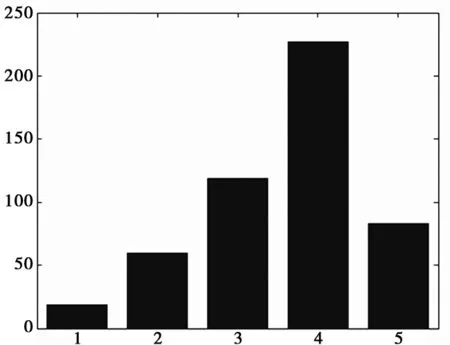
图11 声发射RMS信号每层系数能量柱状图

从分解之后每层细节系数能量来看，第1层、第2层细节系数能量较低，因此第3、第4以及第5层细节系数是该声发射RMS信号的主要部分，在后续分析中通过数学方法将第1、2层细节系数置零，然后将第3、4、5层细节系数与分解之后的近似分量进行重构，得到原始信号的重构信号。该重构信号消除了能量比较低的噪声信号，防止噪声干扰。

3.2 特征值分析

对消噪后的声发射RMS信号进行快速傅里叶变换(FFT)，进行频域分析。在处理之前，首先需要引入频谱矩心的概念：

其中，x(n)为频谱幅值，f(n)为频率。

频谱矩心是一个独立于工艺参数的特征量，即使工艺参数变化，只要砂轮磨损状态不变，频谱矩心这一特征量保持不变。对上述连续进行的180次实验进行快速傅里叶变换，见图12,每磨削5刀为一组，共36组，每组分别求取频谱矩心，结合磨削过程中测量的工件粗糙度，画出矩心图，见图13，分析结果如下：

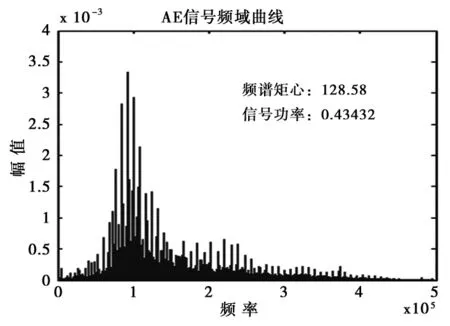
图12 声发射RMS信号的幅频特性

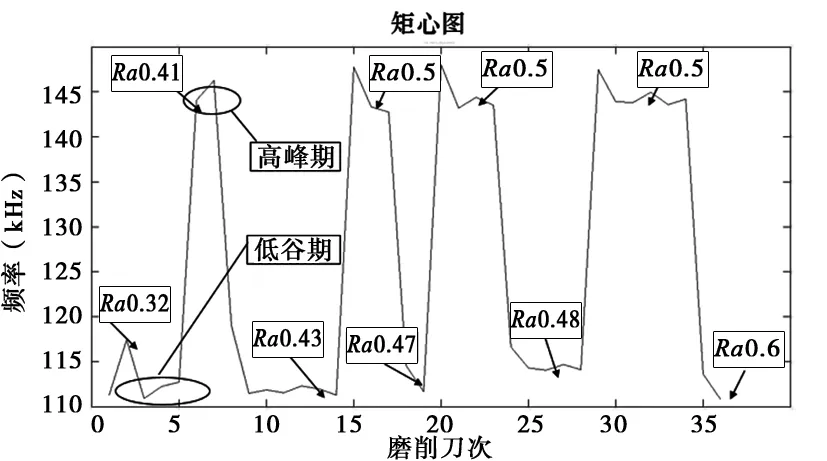
图13 声发射RMS信号频谱矩心图

幅频曲线(图12)显示磨削过程的声发射RMS信号能量集中频率约为100kHz左右，且分布比较集中，超过200kHz或者低于100kHz的信号能量很低。从宏观来看，矩心图(图13)显示随着磨削次数的增加，声发射RMS信号的频谱矩心呈现周期性变化(图中低谷期和高峰期为一周期)；砂轮修整初期，砂轮比较锐利，表现在频谱矩心图上是频谱矩心值比较小，处于低谷期，随着磨削刀次的增加，频谱矩心值会增大，处于高峰期；但当磨削一定刀次之后，频谱矩心的值又会降低到低谷期的，如此往复循环。从细节来看，随着磨削次数的增加，低谷期的持续时间(磨削刀次)会越来越短，相反，高峰期的持续时间会越来越长。因此可知，砂轮修整初期，磨粒比较锋利，砂轮磨损小，此时进行磨削，采集到的声发射信号频率处于低频段；随着磨削次数的增加，砂轮开始磨损，此时采集到的声发射信号处于高频段。随着砂轮磨损的进行，磨削力变大，磨粒由于自锐作用，磨粒破碎，磨粒重新变得锋利，采集到的声发射信号又回到低频段，如此循环。虽然砂轮磨损呈现周期性，但是矩心低谷期持续时间会越来越短，高峰期持续时间会越来越长，延伸下去，低谷期持续时间为0，高峰期占据整个周期，则砂轮需要重新修整；本质上，磨粒虽然具有自锐作用，使磨粒重新变得锋利，但是自锐后的磨粒能够支持的磨削刀次会越来越少，最后，磨粒变得剧烈磨损，磨损严重，已经不能完成自锐作用，砂轮达到寿命，需要重新修整。

矩心图的粗糙度显示，粗糙度会随着磨削次数的增加而越来越大，即工件表面质量下降，侧面反映出砂轮磨损越来越严重。在同一个周期内，矩心处于低谷期的粗糙度始终小于高峰期，即处于矩心低谷期的磨粒磨削出的表面质量总是优于矩心高峰期的。而不同周期内，即使处于矩心低谷期(砂轮锋利)的磨粒磨削出的表面粗糙度并不一定优于高峰期(砂轮磨损)，说明磨粒自锐具有随机性，自锐新生的磨刃既可能改善磨削质量，也可能会恶心加工质量。

频谱矩心数值来看，频谱矩心的变化只有两个区间：低频段从110kHz～120kHz，高频段从142kHz变化到147kHz。同一加工状态，不同工艺参数的磨削过程的高频段和低频段总是相同。而且，低频段的频带范围会略大于高频段频带范围。

3.3 实验验证

为验证此方法的正确性，改变实验参数进行分析。本次实验共进行80次磨削，实验参数如表2所示。

表2 实验参数

对采集的声发射信号，进行能量法消噪与重构，并将其频谱矩心求出，矩心图如图14所示。

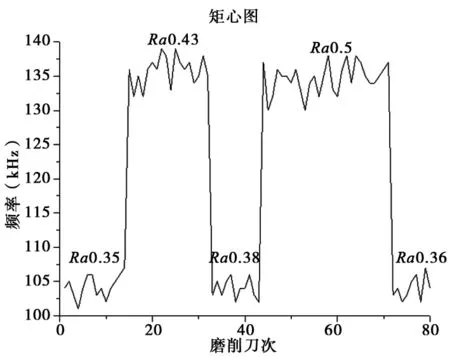
图14 声发射RMS信号频谱矩心图

从图中可以发现，砂轮磨损的声发射频谱矩心仍然具有周期性规律，高频段频率值在130kHz～137kHz之间，低频段频率在103kHz～105kHz之间。说明即使磨削参数发生变化，频谱矩心这一特征值仍然可以表征砂轮磨损规律。

4 结论

砂轮磨损影响因素复杂，统一表征比较困难。本文利用磨削过程中声发射RMS信号频谱矩心这一特征值，表征砂轮的磨损状态，得出砂轮磨损具有周期性。当砂轮修整初期，磨粒锋利时，频谱矩心值较小，随着磨削过程的进行，砂轮磨损加剧，频谱矩心值随之增大。由于磨粒的自锐作用，磨粒破碎脱落，产生新的磨刃，砂轮重新锋利，频谱矩心值又会从高频段降低到低频段，但是随着砂轮的磨损，低频段的持续时间会越来越短，高频段的持续时间会变长，如此循环往复，直至低频段持续时间为零，砂轮剧烈磨损，极难由自锐变锋利，达到使用寿命，需要重新修整。且在砂轮的同一磨损周期内，处于低频段的砂轮磨削出的表面粗糙度会优于处于高频段的砂轮，但在不同周期内，磨削出的工件表面粗糙度不具有可比性，也表明磨粒自锐的随机性。用频谱矩心这一特征值可以形象的表征砂轮磨损过程。