行星滚柱丝杠啮合计算与干涉消除*

陈士云，范元勋，雷建杰

(南京理工大学 机械工程学院，南京 210094)

0 引言

行星滚柱丝杠与滚珠丝杠类似，是一种将螺旋运动转化为直线运动的装置，其主要由丝杆、滚柱以及螺母三部分组成，并巧妙的将行星运动与螺旋运动结合在一起。行星滚柱丝杠具有承载能力强、刚度大、效率高、磨损小以及寿命长等优点，目前，主要应用在航空航天、精密机床、工业机器人、医疗器械以及精密光学仪器等高速重载或精密传动领域[1]。

行星滚柱丝杠啮合接触状态(既啮合间隙量或干涉量)对其传动性能有着很大的影响。行星滚柱丝杠在传动间隙较大时会导致伺服系统难以实现精确的位置控制[2]；同样，过多干涉会导致行星滚柱丝杠预紧力过高，摩擦磨损加剧，寿命降低[3]。行星滚柱丝杠的啮合接触状态成为影响行星滚柱丝杠传动性能的关键因素之一。

在行星滚柱丝杠啮合接触特性分析研究方面，赵英等将行星滚柱丝杠啮合接触区离散成多个平面，在离散的平面内分析行星滚柱丝杠啮合接触状态[4]。Velinsky S A 等基于空间螺旋曲线的Frenet坐标系对行星滚柱丝杠啮合点的位置进行了计算[5]。徐强等对PWG型行星滚柱丝杠啮合接触干涉进行了分析，提出了通过调整滚柱与丝杆啮合中心矩的方法以消除啮合干涉现象[6]。付晓军等通过建立滚柱、丝杆以及螺母螺旋曲面方程，推导出行星滚柱丝杠啮合方程，但并没有考虑啮合干涉问题[7]。

行星滚柱丝杠具有空间螺旋行星传动的基本属性，其啮合点的分布具有空间特点，需要建立空间模型才能对其啮合接触状态进行定量分析。本文基于行星滚柱丝杠的特点，建立行星滚柱丝杠螺旋曲面方程。由于空间螺旋曲面啮合问题的求解十分复杂，为简化计算，对行星滚柱丝杠啮合接触区域进行了分析，并将啮合区螺旋曲面离散成有限个数的点，进而对其啮合接触状态进行快速求解。在SolidWorks中对行星滚柱丝杠建模并虚拟装配，对其干涉量进行分析，分析结果与本文提出的计算方法所得结果一致，验证了方法的正确性。在啮合分析计算的基础上，提出了通过调整丝杆螺纹几何中径的方法以消除行星滚柱丝杠在实际装配过程中的干涉问题，理论分析计算结果与实际加工装配情况一致，验证了方法和分析结果的有效性。

1 螺旋曲面方程

1.1 坐标系的建立

根据行星滚柱丝杠的结构特点，建立如图1所示的空间坐标系。主要有固定坐标系(Oxyz)、滚柱坐标系(ORxRyRzR)、滚柱截面坐标系(Orxryrzr)、丝杆截面坐标系(Osxsyszs)、螺母截面坐标系(Onxnynzn)。图中，rs、rr、rn分别表示滚柱、丝杆和螺母螺旋面几何半径(即螺纹中径)，a为啮合中心距，即滚柱轴线与丝杆轴线之间的距离。

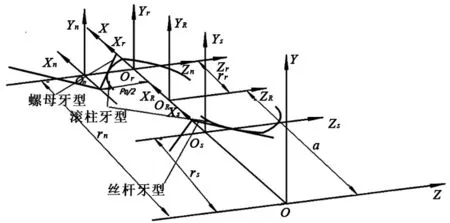
图1 啮合接触分析坐标系

1.2曲面方程

行星滚柱丝杠牙型轮廓如图2a、图2b、以及图2c所示，图中P0表示螺距，Rr为滚柱型面圆弧半径，β为型面牙型半角。

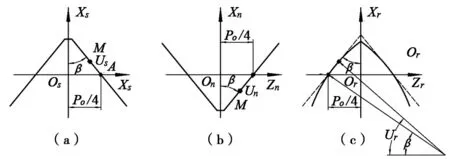
图2 丝杆、螺母及滚柱牙型轮廓

考虑到对称性，仅对行星滚柱丝杠滚柱、丝杆以及螺母一侧螺旋曲面建立参数方程。

滚柱左侧母线上一点M在滚柱坐标系中的参数方程为：

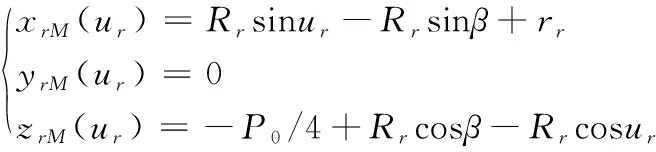
(1)

式中，ur为角参变量，xrM、yrM、zrM为M点在滚柱坐标系中坐标。

该母线绕滚柱轴线做螺旋运动所形成的螺旋曲面参数方程为[8]：

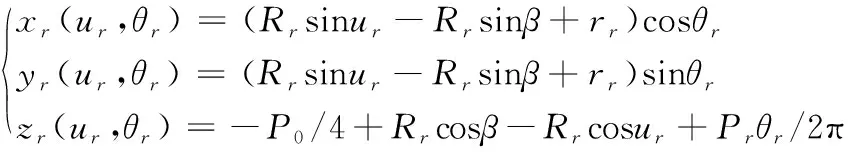
(2)

式中，θr为滚柱母线绕滚柱轴线zr的转角，Pr为滚柱导程，一般有Pr=P0。

同理，丝杆右侧母线绕丝杆轴线z形成的螺旋曲面可以分别表示为：

(3)

式中，θs为丝杆右侧母线绕丝杆轴线z的转角，Ps为丝杆导程，有Ps=nsP0，ns为丝杆头数，us为参变量。

螺母右侧母线绕螺母轴线z形成的螺旋曲面可以分别表示为：

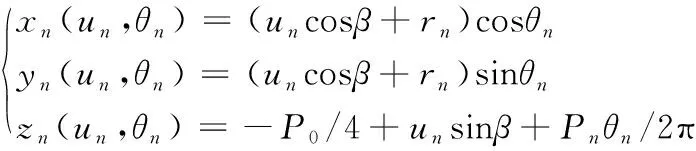
(4)

式中，θn为螺母右侧母线绕丝杆轴线z的转角，Pn为螺母导程，有Pn=nnP0，nn为螺母头数，un为参变量。

螺母螺旋面与丝杆螺旋面坐标系与固定坐标系重合，滚柱坐标系与固定坐标系满足下式:

(5)

根据矩阵运算法则，式中需假设一个新的参数t=tR=1[8]，a啮合中心距距离。

2 啮合状态计算

啮合状态计算的目的是：通过改变行星滚柱丝杠丝杆、滚柱、螺母螺纹的相关参数，理论上精确控制行星滚柱丝杠的啮合干涉量或啮合间隙量。

由于用解析法计算一对空间螺旋曲面的啮合问题十分复杂，文献[4]将螺旋曲面离散成有限个相互平行的平面内的曲线，然后对曲线接触情况进行分析，但该方法对复杂螺旋曲面的求解依然有一定的难度。本文对文献[4]方法进行改进，将螺旋曲面离散成有限个数的点，求解相应点的轴向距离，从而对行星滚柱丝杠啮合状态进行精确求解。以滚柱与丝杆啮合状态仿真计算为例，具体步骤如下：

(1)将滚柱、丝杆螺旋曲面离散成有限个点。为减小计算量，仅对滚柱、丝杆螺旋曲面可能出现啮合接触的区域(如图3阴影部分)离散成有限个点。得到行星滚柱丝杠端面(XOY平面)内滚柱、丝杆啮合接触区离散点坐标PRSi(xRSi,yRSi)。

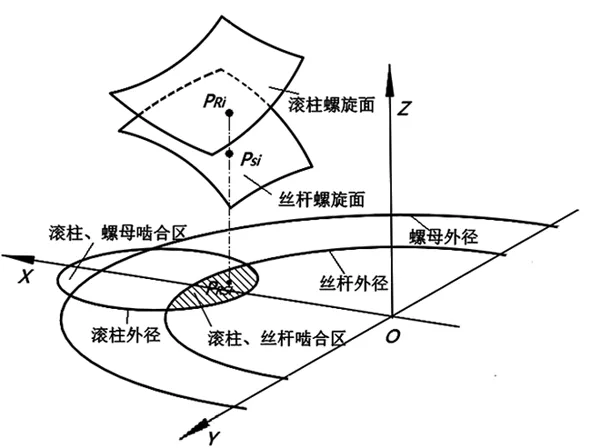
图3 啮合接触区域示意图

(2)求解PRSi点处滚柱与丝杆螺旋曲面上点轴向坐标值。将式：

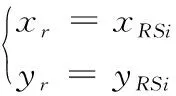
(6)

代入滚柱螺旋曲面方程(2)可以求解出PRSi点处滚柱螺旋曲面坐标PRi(xRSi,yRSi,zRi)。同理将式(6)代入式(3)可以求出PRSi点处丝杆螺旋曲面坐标PSi(xRSi,yRSi,zSi)。

(3)求解啮合干涉量或啮合间隙量。通过计算点PRi、PSi在z轴方向坐标差值即可得出螺旋曲面轴向干涉或轴向间隙量。同时沿z轴坐标方向，坐标差值最小点为啮合点。

(4)改变滚柱或丝杆螺纹参数，循环计算，直到得到满足实际需求啮合状态，得到实际装配螺纹参数。

滚柱与螺母的啮合状态计算和滚柱与丝杆计算类似，不再赘述。

3 算法实现与验证

在Matlab中对上述算法进行编程实现。为验证算法的正确性，通过改变丝杆、螺母螺纹几何中径，使用本文计算方法计算行星滚柱丝杠啮合干涉量，同时在SolidWorks中建立行星滚柱丝杠虚拟装配模型[9]，对行星滚柱丝杠啮合干涉量进行计算，将所得到的结果进行对比。

根据行星滚柱丝杠运动特性，计算出如表1所示行星滚柱丝杠理论几何参数[10]。

表1 行星滚柱丝杠理论几何参数

使用本文所述啮合状态计算方法对表1参数行星滚柱丝杠啮合状态进行计算，计算时丝杆和滚柱的啮合中心距采用理论值a=13mm。

在对啮合状态进行计算时，本文方法计算结果为螺旋面轴向距离，负值为啮合干涉状态，正值为啮合间隙状态。在SolidWorks中进行虚拟装配时，啮合干涉状态计算所得结果为干涉体积,虚拟装配模型如图4所示。滚柱和丝杆啮合干涉量计算部分结果如表2所示。

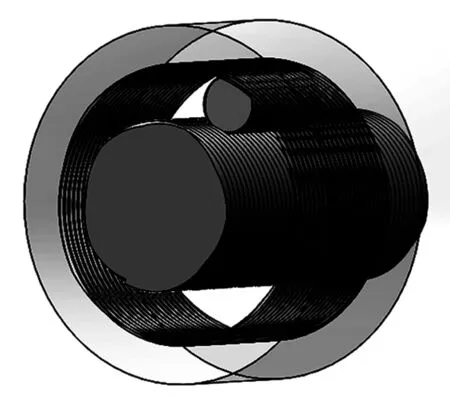
图4 行星滚柱丝杠虚拟装配

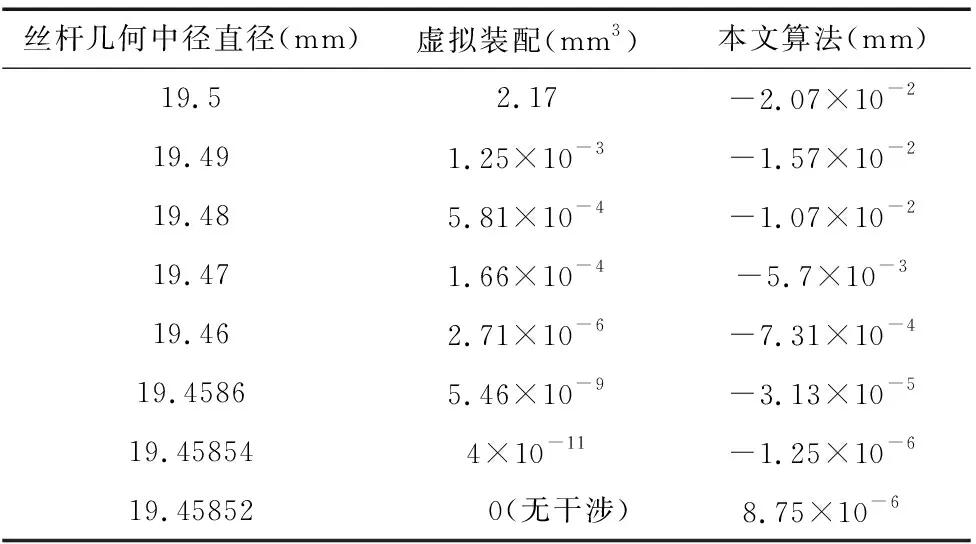
丝杆几何中径直径(mm)虚拟装配(mm3)本文算法(mm)19.52.17-2.07×10-219.491.25×10-3-1.57×10-219.485.81×10-4-1.07×10-219.471.66×10-4-5.7×10-319.462.71×10-6-7.31×10-419.45865.46×10-9-3.13×10-519.458544×10-11-1.25×10-619.45852 0(无干涉)8.75×10-6

从表2中可以看出，随丝杆几何中径的减小，SolidWorks中虚拟装配计算所得到的干涉量体积变化趋势与本文算法所计算干涉量变化趋势一致。虚拟装配与本文算法计算所得结果均显示为丝杆几何中径在19.45852mm时，存在啮合间隙，丝杆几何中径在19.45854mm时存在啮合干涉，可得两种计算方法所得零侧隙啮合状态下丝杆中径直径均为(19.45852mm，19.45854mm)区间内，本文方法计算结果与SolidWorks中虚拟装配计算结果吻合。且通过本文方法计算，可将滚柱和丝杆轴向螺旋面轴向距离控制在10-5mm以内。滚柱和螺母之间啮合干涉计算验证与滚柱和丝杆计算方法相同，其计算结果与虚拟装配计算结果吻合。此外，在对多种不同规格行星滚柱丝杠进行计算验证时，本文方法计算结果均与虚拟装配计算结果相符，而且均可以将轴向间隙控制在0.001mm以内，完全满足实际工程需求，证明了算法的正确性及实用性。

4 啮合干涉消除

由上文计算可知，当行星滚柱丝杠丝杆和滚柱以理论中心距a=rr+rs进行装配时，会出现严重的干涉现象，计算结果与文献[6，10]所述相同。对表1中所给参数行星滚柱丝杠进行计算时，得到丝杆与滚柱啮合轴向距离分布如图5左图所示，可以看出，滚柱与丝杆啮合区域干涉明显。实际计算结果中螺旋面最小轴向距离为-0.0207mm，啮合干涉区很大，啮合点在行星滚柱丝杠端面内投影坐标为Pxy(9.7648,0.3191)。

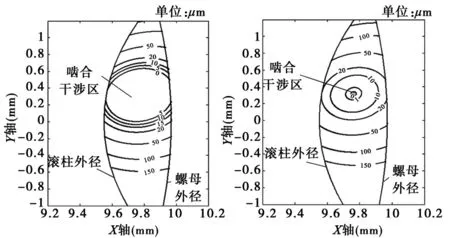
图5 滚柱与丝杆轴向距离分布

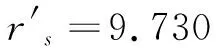
通过实例计算可以看出，在通过调整丝杆几何中心距调整丝杆与滚柱的啮合干涉量时，不改变啮合点在行星滚柱丝杠端面内投影位置。在对多种其它规格行星滚柱丝杠进行计算时，所得到结果相同。通过调整丝杆几何中径，在达到消除啮合干涉的同时，不影响行星滚柱丝杠的运动特性[11]。

在按理论参数对螺母与滚柱啮合干涉量进行计算时，螺母与滚柱间无干涉现象，与实际装配情况相符。在对行星滚柱丝杠进行设计时，可以通过适当调整螺母几何中径值实现对滚柱和螺母之间的预紧量或间隙量进行调节，且不改变滚柱与螺母啮合点在行星滚柱丝杠端面内投影位置，即不改变行星滚柱丝杠的运动特性。

5 结论

(1)文中通过建立了行星滚柱丝杠螺旋曲面啮合的空间坐标系及螺旋曲面方程，将螺旋曲面离散成有限个点，对行星滚柱丝杠啮合干涉量定量分析计算，并通过虚拟装配验证了方法的正确性；

(2)通过对丝杆、螺母几何中径对行星滚柱丝杠装配干涉量影响分析计算，提出调整丝杆、螺母几何中径的方法实现消除或控制啮合干涉量，且对丝杆、滚柱螺纹几何中径的调整不改变行星滚柱丝杠运动特性，在实际加工装配中，通过调整丝杆螺纹几何中径有效的控制了干涉问题。