非整平自由设站在轨道快速测量中的应用

马文静

(中铁工程设计咨询集团有限公司，北京 100055)

1 概述

不论是有砟轨道高速铁路还是无砟轨道高速铁路，均需要进行轨道测量及轨道精调，使建成轨道的平顺性满足高速行车的要求[1-3]。传统的轨道测量方法是将全站仪架设在脚架上并精确整平，然后基于线路两侧的轨道控制网(CPⅢ)进行自由设站测量[4-7]，在设站精度满足规范要求之后，才能开始轨道测量工作。这种方法的弊端在于每次搬站后均需要对全站仪进行精确整平，不仅花费时间较多，降低工作效率，而且对测量人员的操作技能要求也比较高。在运营高速铁路普遍采用“天窗修”[8]的线路养护模式下，这种作业效率较低的轨道测量方法已不适应现实的需要。

为了提高轨道测量作业的工作效率，一个可行的方法是去掉全站仪精确整平的操作流程，同时也不再进行人工搬站。提出一种将全站仪架设在轨检小车上，与之保持刚性连接的新型轨道测量装备，其结构如图1所示。在开展轨道测量工作时，全站仪与轨检小车一同移动，当需要进行自由设站测量时，则将轨检小车停下并进行自由设站测量工作。这种轨道测量新方法，由于没有了搬站及精确整平的过程，节省了大量的时间，将使轨道测量效率较之传统方法成倍提升。

图1 全站仪与轨检小车连接结构示意

全站仪架设在轨检小车上并进行自由设站时，其状态是非整平的。通过观测一定数量且三维坐标已知的CPⅢ控制点，解算全站仪的站心三维坐标，从而对轨检小车当前所处的位置进行准确定位。轨道线路在曲线段存在超高，在线路纵向上存在纵坡，以及由于施工、运营等原因造成的各种轨道不平顺，使得全站仪的非整平状态较为复杂，必须建立一种通用、准确的站心三维坐标解算数学模型，使之能够适用于各种非整平状态，并保证站心三维坐标的解算精度。

2 站心三维坐标解算的理论模型

全站仪在非整平状态下观测CPⅢ控制点，其实质是建立了一个以站心为坐标原点、任意定向且Z轴不与水平面垂直的空间直角坐标系，所有的观测值均处于这个坐标系之下；另一方面，已知三维坐标的CPⅢ控制网在本质上是一个Z轴垂直于水平面的空间直角坐标系。两个空间直角坐标系之间的轴系关系，可以采用欧拉角分解为三次绕轴转动，并利用方向余弦矩阵联系起来。

设绕Z，X，Y轴依次旋转的角度分别为θ、φ及γ，平移参数分别为ΔX、ΔY、ΔZ，尺度比为μ，原坐标系下用(x、y、z)表示点坐标，新坐标系下用(u、v、w)表示点坐标，则两个空间直角坐标系间的转换关系见式(1)[9]

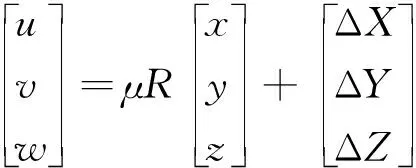
(1)

式(1)为非线性方程组，包含三个旋转角、三个平移量及一个尺度因子，一共7个未知数，在最少已知三个公共点的情况下即可求解。R为基于三个欧拉旋转角组成的3阶方向余弦矩阵[10]，如式(2)所示。该3阶矩阵的9个元素之间相互不独立，而且直接以角度为未知数还存在象限判断的问题，在对方程进行线性化时会存在较大的精度损失，难以保证解算成果的准确性，需要寻求一种高精度且实用的计算方法。

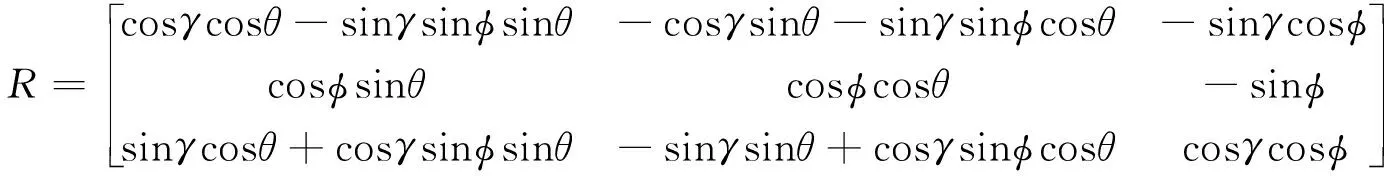
(2)

3 站心三维坐标的实用算法

3.1 罗德里格矩阵

定义反对称矩阵S

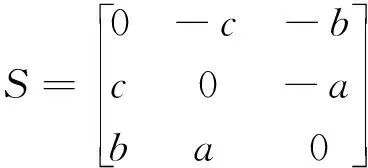
(3)

式(3)中a、b、c为三个相互独立的未知数，则方向余弦矩阵R可由S构成的罗德里格矩阵[11-13]表示为

R=(I+S)(I-S)-1

(4)

式(4)中I为3阶单位矩阵。如此构建的矩阵R中的各元素间相互独立，不仅便于开列线性化法方程，也便于未知数的初值求解。

3.2 七参数初值求解

设有三个公共点，则可首先根据边长之比计算尺度因子，有

(5)

将式(4)代入式(1)，利用点1及点2的坐标开列方程，并相互作差消去三个平移参数并整理[6]，有

(6)

式(6)为关于未知数a、b、c的三个线性方程组，由于只含有两个独立方程，不能解算三个未知数，需再利用点1及点3开列方程组，联立求得未知数a、b、c，然后利用式(4)计算得到R矩阵，最后根据式(7)计算两个空间直角坐标系之间的平移参数。

(7)

3.3 最小二乘法求解模型

在全站仪非整平自由设站中，通常会观测6～8个CPⅢ控制点，对所有点按照式(1)开列方程求解七参数时会存在多余观测，需要采用最小二乘法平差求解最或然概率下的结果。首先可通过上述七参数初值计算方法，任意选择3个点求解七参数初值。由于从6～8个点中任选3个点存在多种选法，可计算出多组七参数初值。考虑到CPⅢ控制点位移导致的坐标不准确、点位网形强度等因素，并确保最小二乘平差计算中能够迭代收敛，七参数初值特别是方向余弦矩阵初值应该具有较好的精度，可按照式(8)选择L2范数定义下值最小的一组。

(8)

初值求解完成后，将式(3)代入式(4)，经整理得到以a、b、c表示的方向余弦矩阵R，再将R代入式(1)并整理，有

(9)

对式(9)进行线性化，按照最小二乘法开列误差方程并求解[14-15]

(10)

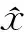
3.4 站心坐标计算及精度估计

全站仪非整平状态下自身空间直角坐标系的原点就是其站心，三轴坐标值均为零；基于式(1)，解算得到的三个平移参数ΔX、ΔY、ΔZ就是站心在CPⅢ坐标系下的坐标。利用式(1)计算经坐标变换后的CPⅢ控制点坐标，并与已知坐标进行比较，利用式(11)计算各个控制点每个坐标轴向的坐标残差

(11)

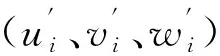
(12)

式(12)中，n为非整平自由设站时所观测的CPⅢ控制点个数，站心坐标的坐标残差可由式(11)所计算的每个CPⅢ控制点坐标残差的平均值来估计。按照误差传播定律，站心坐标在三个轴向的坐标中误差可根据式(13)估算

(13)

4 实测数据分析

为验证该方法在全站仪各种非整平状态下的通用性及计算的准确性，在某无砟高速铁路上进行了非整平自由设站试验。试验在线路左线开展，每120 m进行一次非整平自由设站测量，每次设站观测8个CPⅢ控制点，站与站之间搭接4个CPⅢ控制点。试验区段总长约12 km，包含2条右偏曲线，1条左偏曲线，圆曲线半径分别为14 000 m、9 000 m、14 000 m，设计超高分别为75 mm、120 mm、85 mm。试验共计进行124次非整平自由设站测量，每次设站测量时，全站仪在线路横向及纵向与水平面之间的角度如图2所示。

图2 全站仪非整平状态下与水平面的倾角

由图2可见，对全站仪非整平状态进行线路横向及纵向分解，得到这两个方向全站仪与水平面之间的倾角。在线路横向，由于受曲线超高的影响，倾角变化的幅度较大；以右偏曲线倾角为负值，左偏曲线倾角为正值，则直线地段的倾角约为0°；75 mm，120 mm及85 mm曲线超高地段的倾角分别约为-2.8°、4.6°及-3.2°，缓和曲线地段的倾角则是从直线到圆曲线之间的平缓过渡。线路纵向坡度一般不会太大，以上坡倾角为正值，下坡倾角为负值，则本试验段在纵向的倾角变化范围约为-0.2°～0.2°。由上述分析可知，本次试验的124次非整平自由设站测量包含了各种轨道测量工况下的非整平状态，具有较好的代表性。

非整平自由设站下站心坐标解算完成后，利用式(13)计算各CPⅢ控制点的坐标残差，通过对每一站所观测6～8个CPⅢ控制点三个坐标分量的残差进行分析，可以对CPⅢ控制点的稳定性进行评价。对于变形明显及移动的CPⅢ点，则将其剔除，使其不参与站心三维坐标的解算过程，从而达到控制测量精度的目的。表1所示为某次非整平自由设站所观测的7个CPⅢ控制点全部参与解算后所得的坐标残差情况，点057325、057327、057329及057331的高程残差均较大，其中点057329的高程残差最大，且该点东坐标、北坐标的残差分别为-30.37 mm，-22.16 mm，也是所有点当中最大的，因此可以判定点057329大概率发生了变形，不应参与数据解算，应当做粗差剔除；在未剔除粗差的情况下，计算得到的站心三维坐标的东、北、高为494 550.463 5 m，4 376 136.655 1 m，15.342 4 m，对应的坐标中误差为4.77 mm，3.44 mm，20.52 mm，表明所得的站心三维坐标精度很差，不能满足使用要求。

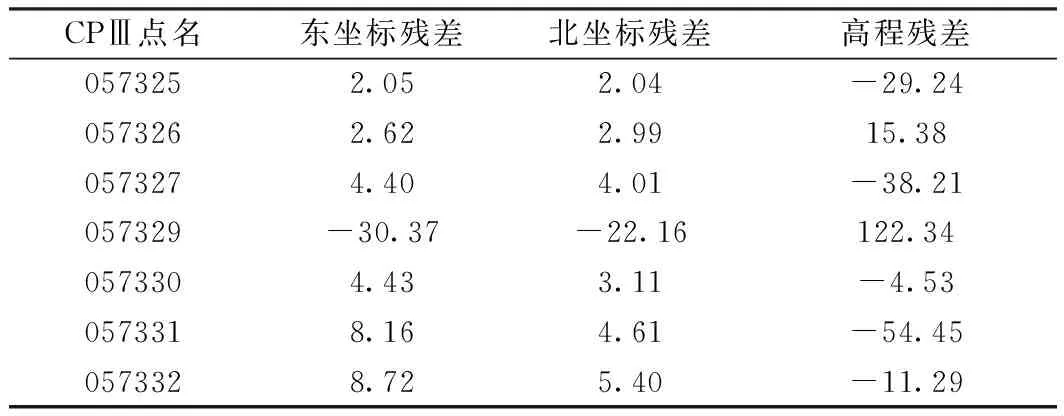
表1 粗差剔除前的CPⅢ控制点坐标分量残差 mm

由于该站共观测了7个CPⅢ控制点，具有足够的多余观测，因此可将点057329当做粗差剔除。对剩余的6个CPⅢ控制点数据重新计算，得到的坐标残差见表2所示，可见每个点在三个坐标分量上的残差均小于2 mm，说明这6个CPⅢ点的兼容性较好，精度均匀。解算所得的站心三维坐标为494 550.467 6 m、4 376 136.658 0 m、15.308 7 m，对应的坐标中误差为0.32 mm、0.24 mm、0.30 mm，表明解算结果达到了较高的精度。与未剔除点057329之前的计算结果相比，坐标中误差大幅度缩小且均小于0.7 mm，站心三维坐标的变化量为-4.1 mm、-2.9 mm、33.7 mm，进一步说明了点057329不仅造成了站心坐标中误差偏大，同时也使站心三维坐标产生了较大的偏差。

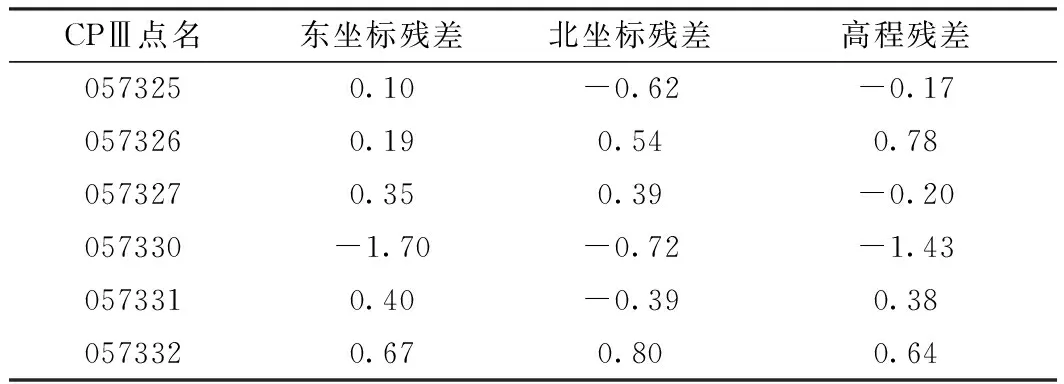
表2 粗差剔除后的CPⅢ控制点坐标分量残差 mm

按照上述方法对所有124站数据进行处理，并保证每一站至少有5个点参与站心三维坐标解算，所得CPⅢ控制点坐标残差的分布情况如图3所示。经统计，东坐标残差绝对值大于2 mm的比例为0.5%，北坐标残差绝对值大于2 mm的比例为0.7%，高程残差绝对值大于2 mm的比例为0.7%。坐标残差分布表明，本次非整平自由设站试验所采用的CPⅢ控制点整体精度良好。

图3 CPⅢ控制点残差分布

如图4所示，在东坐标、北坐标及高程三个轴向上，站心坐标的中误差均未超过0.7 mm。

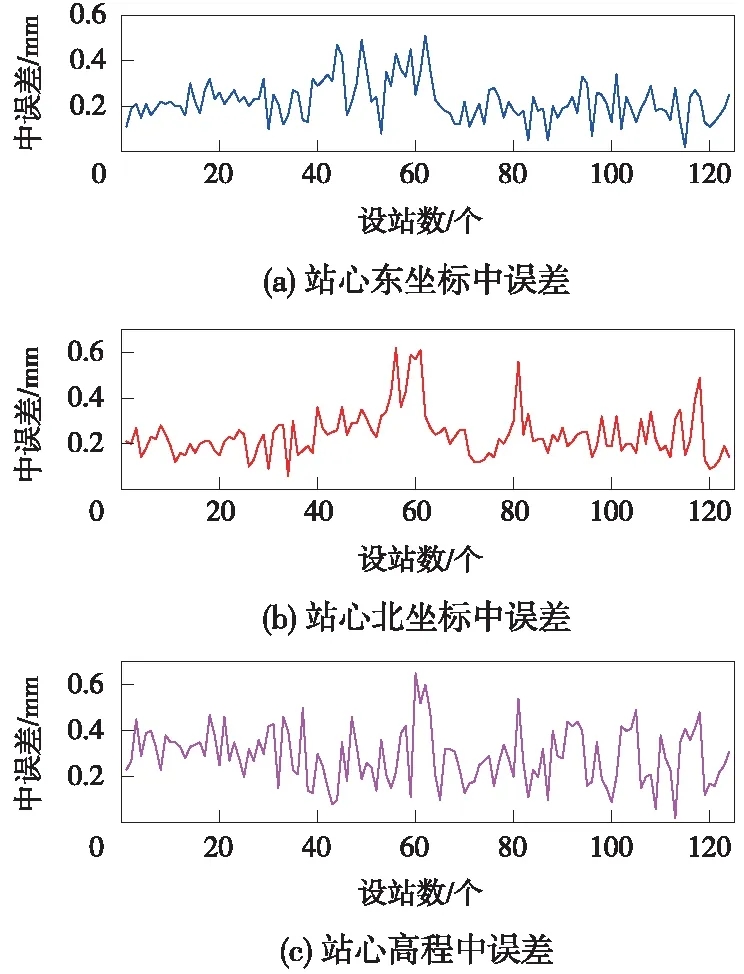
图4 站心坐标中误差分布

《高速铁路工程测量规范》(TB10601—2009)要求在全站仪整平自由设站的前提下，站心坐标三个轴向中误差应小于0.7 mm，坐标残差应小于2 mm，由此可见，在CPⅢ控制网精度良好的情况下，进行全站仪非整平自由设站并采用该方法解算站心三维坐标、站心坐标中误差及CPⅢ控制点坐标残差等成果，达到了整平自由设站所要求的各项指标精度。

5 结束语

利用全站仪非整平自由设站的方法，可以省去传统轨道测量方法中对全站仪搬站及精确整平的工作过程，不仅大幅度提高了轨道测量的作业效率，而且降低了对作业人员的技能要求，具有巨大的技术优势。采用该方法的关键环节在于准确可靠地解算站心三维坐标，并给出相应的精度评定指标。鉴于此，给出了非整平自由设站下站心三维坐标解算的理论模型及实用算法，并利用运营高速铁路高精度的CPⅢ控制网进行了124站各种线路状况下的非整平自由设站测量试验。测试结果表明，该方法能够适应轨道测量过程中的各种倾斜状态下的数据解算，根据控制点坐标残差能够发现并剔除粗差点， 99%的CPⅢ控制点坐标残差均小于2 mm，站心坐标东、北、高程三个方向的中误差均小于0.7 mm，计算结果准确可靠，满足相关规范标准，达到了轨道测量对作业精度的要求。