基于小波神经网络模型的高铁沉降预测方法研究

薛 骐

(中国铁路设计集团有限公司，天津 300000)

目前，高铁沉降预测方法大体上可以分为3种类型：曲线拟合法、基于固结理论的数值计算方法以及分层总和方法。其中，曲线拟合法适用范围较广，内容比较丰富，包括三点法、拓展双曲线法和Asaoka法等[1]。此外，卡尔曼滤波法是目前高铁沉降预测的主流方法，具有很强的自适应性和抗干扰性[2-4]。20世纪以来，随着神经生物学的快速发展，神经网络技术也应运而生。其中，小波神经网络的概念是在1992年率先由法国著名的信息科学研究机构IRISA的Zhang Qinghua等[5]提出。在大西线侯马西站轨道变形监测中，笔者编写了通用小波神经网络预测软件来分析该方法的可行性和实用性，并分别与卡尔曼滤波进行比对，证明小波神经网络在高铁沉降预测中的重要参考价值。

1 小波神经网络模型方法研究

小波神经网络的基本思想是使用小波元替代传统神经网络的神经元，使用已知的小波函数代替Sigmoid函数作为训练中的激活函数，然后通过仿射变换建立小波与神经网络之间的关系。其本质是对小波进行分解、平移变换、缩放变换，从而具有小波分解中一般逼近函数的性质，其最重要的特点是在时域和频域上同时具有良好的局部化性能。

小波神经网络具有以下3个特点和需要注意的事项：①在选取小波函数的时候，需要根据样本数据的特征和训练方法等特点进行确定，避免盲目跟从。②小波神经网络平移参数和伸缩参数的确定很重要，它能够优化训练过程，达到全局目标，从根本上避免了局部最优的情况。③其收敛速度快，学习能力和函数逼近能力比较强。

1.1 小波神经网络的学习算法

小波神经网络是由小波分析方法和神经网络方法相结合而产生，它兼具了两者的优点。从结构方面可以分为松散型小波神经网络和紧致型小波神经网络。松散型小波神经网络中小波分析和神经网络两部分独立，紧致型小波神经网络在结构上将两者融合在一起，充分体现了两者之间的有机组合关系。传统神经网络的Sigmoid基函数[6]使用小波基函数来代替，将隐含层用小波函数进行表达，并用小波函数的尺度参数和平移参数取代输入层和隐含层的权值及阈值。其结构[7]如图1所示。

图1 小波神经网络结构

小波神经网络的学习算法通常包括以下几种：梯度下降法、矩阵求逆法和正交搜索法等[8]。考虑到小波神经网络的权值和输出都是线性关系，不存在BP神经网络那样局部极限小的问题，所以选择紧致型小波神经网络的梯度下降学习方法。其网络结构由输入层、隐含层和输出层构成。

如图1所示，输入向量数据为x=[x1，x2，…，xn]T，输出向量数据为y=[y1，y2，…，ym]T，输出向量数据的期望值为d=[d1，d2，…，dm]T，输入层到隐含层的权值设定为ωjk，隐含层到输出层的权值为ωij，其中隐含层的伸缩平移参数分别为aj、bj，设隐含层神经元数量为N。其中ωjkωij初始值取0.5，伸缩参数aj取1，平移参数bj取0.5，初始值的设定在这里没有固定取值，因为在后续运算回调过程中会对这几个值进行优化。由上可得i=1，2，…，m，j=1，2，…，N。得t时刻小波神经网络的模型

(1)

结果检验的误差函数采用均方差误差

(2)

其中，P为训练样本的集合。令

有

(3)

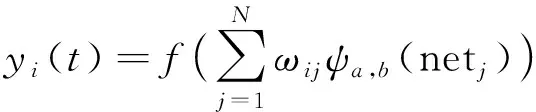
(4)

根据选用的梯度下降法，各个参数的回调过程如下

ωjk(t+1)=ωjk(t)+ηjkΔωjk(t)

(5)

ωij(t+1)=ωij(t)+ηijΔωij(t)

(6)

aj(t+1)=aj(t)+ηaΔaj(t)

(7)

bj(t+1)=bj(t)+ηbΔbj(t)

(8)

上式中，ηjk，ηij，ηa，ηb分别为ωjk、ωij、aj、bj的学习效率，对其求偏导得公式(9)～公式(12)

(9)

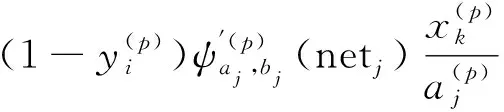
(10)

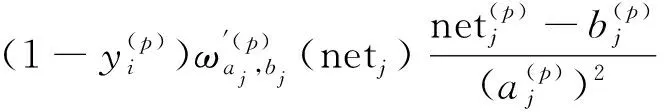
(11)

(12)

1.2 小波神经网络的结构设计

小波神经网络的结构设计主要包括两部分：小波函数的确定和隐含层节点数量的选择。选取合适的小波函数和隐含层节点数量是小波神经网络能否对样本数据进行训练并成功预测的重要因素。

目前，应用较为广泛的小波函数有：Harr小波、墨西哥帽小波、Morlet小波和Gausse小波等几种方法[9]，实际应用中尚没有规范的应用标准。Morlet小波具有较好的抗干扰性、函数逼近能力强、计算性能稳定等特点，在诸多刊物上发表的文章采用该方法均取得了良好的实验结果，例如侯泽宇[10]、王宇谱[11]、李超[12]等。考虑上述几点因素，在该沉降预测软件系统中使用了Morlet小波[9]作为激励函数。该方法公式如下

y=cos(1.75x)e-x2/2

(13)

小波神经网络的隐含层节点数量对训练过程和预测结果具有较重要的影响。当前隐含层节点数量的确定方法有实验法和经验公式法。其中，实验法速度比较慢，且适应效果比较差，本文采用经验公式

(14)

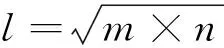
(15)

0.51

(16)

(17)

从实际使用的角度考虑，并结合小波神经网络在其他应用方面的效果，采用公式(17)的计算方法，算得隐含层节点数量l=24。

1.3 小波神经网络的归一化处理

小波神经网络归一化的目的是为了消除观测数据之间数量级之间的差别，防止因样本数据的数量级差异对预测结果造成结果不准确、精度不高等影响。

归一化算法如下[14]

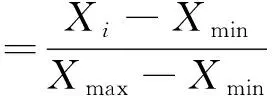
(18)

反归一化算法如下[15]

Xi=X归(Xmax-Xmin)+Xmin

(19)

其中，X代表的是样本数据，Xmax、Xmin分别代表样本数据中的最大值和最小值。

2 实验数据

本次实验数据来源于大西线侯马西站轨道变形监测CPⅢ监测点数据，该监测点周围正在新建楼房，导致该轨道发生相应的沉降现象。该数据监测时间从2011年12月22日到2014年5月23日，监测周期大概为一个月。共28组数据，取前21组数据作为实验数据，后7组数据作为预测数据的参考值，用来评价小波神经网络方法的精度。为了更全面的评价小波神经网络方法的全面性，采用监测区中心以及监测区边缘两个比较有代表性的点得到的两组数据，对该方法的可用性进行探讨分析。

3 小波神经网络与卡尔曼滤波对比分析

3.1 第一组实验

第一组实验数据和解算图像及相关评价参数指标如表1。

表1 第一组实验数据实测结果 mm

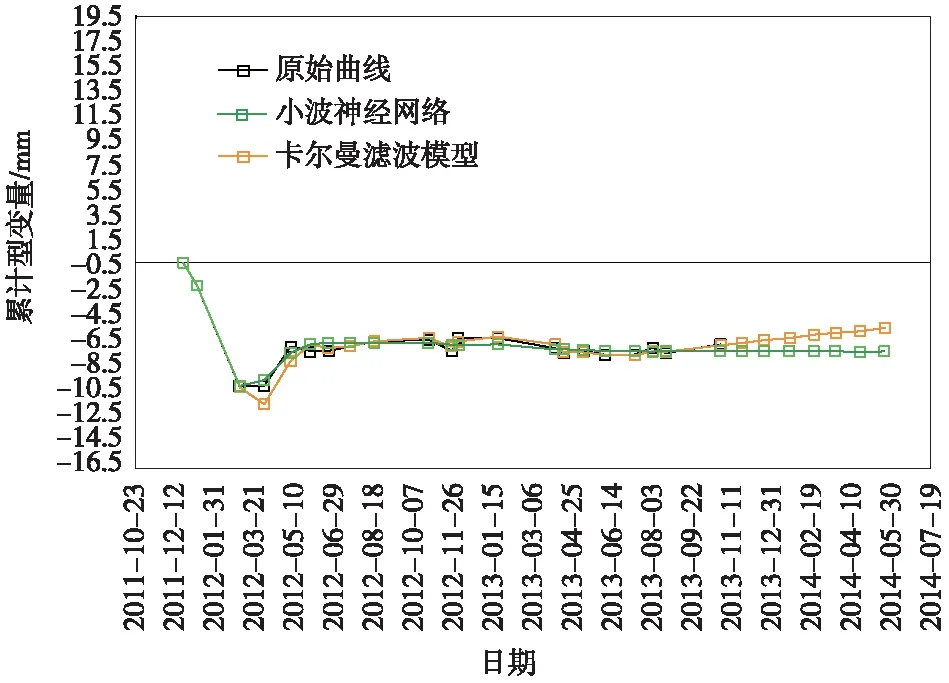
图2 第一组实验数据处理结果

由图2可以看出，小波神经网络的拟合效果和预测结果都比较合适。前期，卡尔曼滤波与测量结果的拟合程度还不是很好，但是经过几次观测数据的自适应调整后，卡尔曼滤波具有很好的匹配程度。但是在观测后期，由于最后两组数据波动比较大，导致卡尔曼滤波预测的结果与实际结果偏差较大。而小波神经网络其整体性拟合程度较好，而且在最后的预测结果中容错性较好，与实际结果有较好的匹配度。

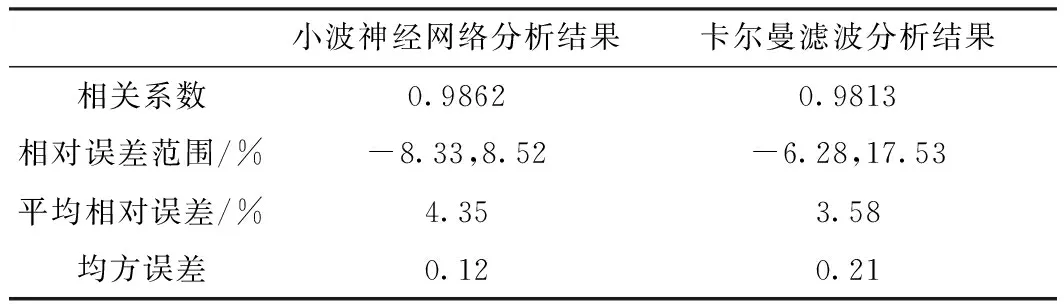
表2 第一组实验数据拟合结果评价参数

表3 第一组实验数据预测结果 mm

综上所述，结合表2、表3数据可以看出，在该点的沉降观测及预测效果上，小波神经网络具有很强的拟合能力和预测能力。在后期的数据统计中，相关系数、相对误差范围、平均相对误差、均方误差这4个评价要素均比卡尔曼滤波方式得到的结果稍好。

3.2 第二组实验

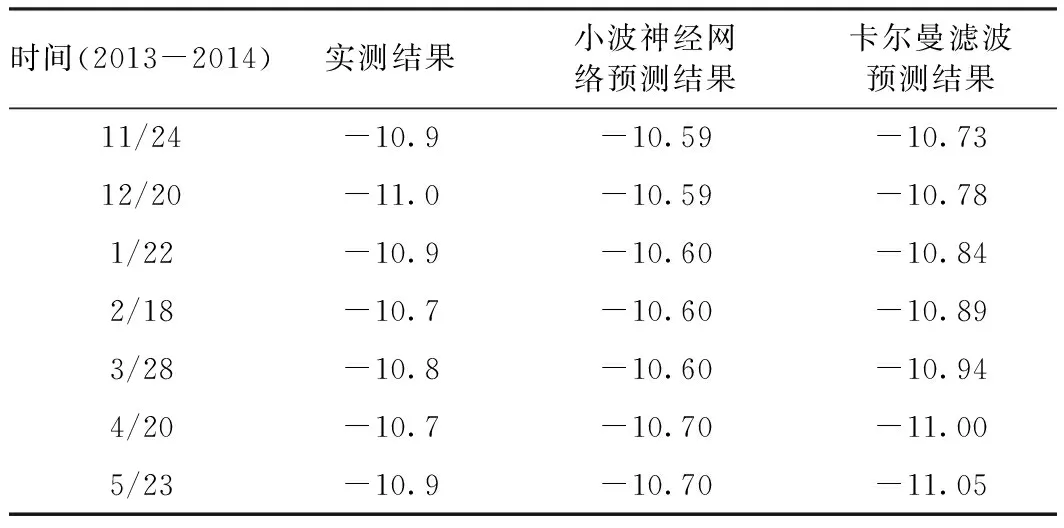
第二组实验数据和解算图像及相关评价参数指标如表4～表6和图3。

由图3可以看出，在拟合效果上两种方式各有优势，从总体结果上看，卡尔曼滤波拟合效果更好，但是在预测结果上不太平稳。从原理上来讲，沉降观测的结果应该是趋近于稳定，而卡尔曼滤波的预测结果在持续变动。通过比较可以看出，小波神经网络在拟合方面稍显不足，但是在沉降预测方面很稳定。

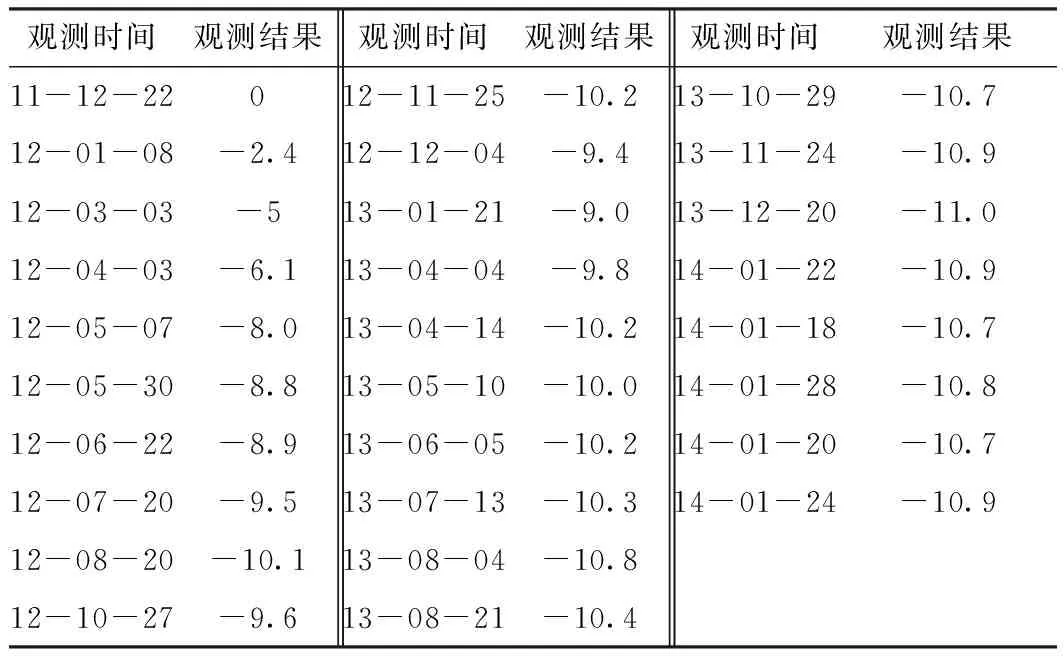
表4 第二组实验数据实测结果 mm

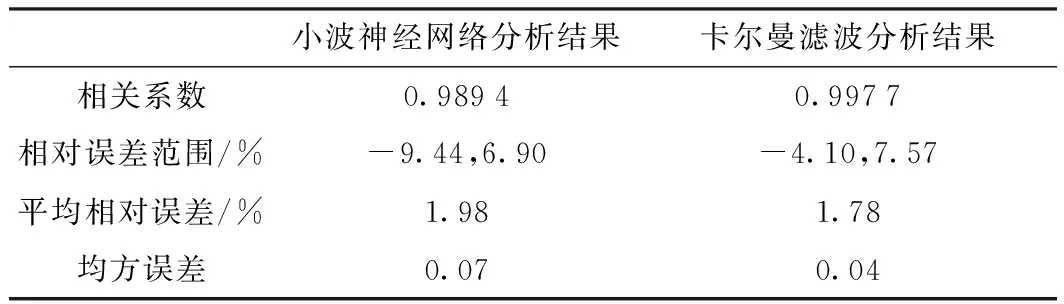
表5 第二组实验数据拟合结果评价参数

图3 第二组实验数据处理结果

4 结束语

(1)使用时，需根据实际情况来选择小波函数并设置隐含层节点计算方法，这对该方法结果的精确度具有重要影响。

(2)小波神经网络方法具有很好的学习能力和相应的训练速度。

(3)相较于卡尔曼滤波方式，小波神经网络拟合程度较好，预测结果稳定。在高铁沉降观测预测中，其收敛速度、容错能力、预报效果均得到了有效证实，在未来的应用中会具有更加广泛的应用前景。

5 展望

小波神经网络具有很多优点，在应用中也存在一些不足，如训练算法和小波函数的选择、隐含层及其节点数据的确定等，需要通过大量的实验进行对比分析。今后的工作中，需加强对上述问题的探讨研究。