基于改进PSO算法的直接空冷背压模型辨识

白建云 ，曲 燕 ，孟新雨 ，李永茂 ，冯 赓

（1.山西大学 自动化系，太原 030013；2.山西大学 数学科学学院，太原 030006；3.山西平朔煤矸石发电有限公司，朔州 036800）

燃煤电厂空冷技术因其卓越的节水降耗优势，逐渐成为新、改、扩建机组的首选。直接空冷系统具有无中间介质和二次换热、综合换热效率高、初期投资较低、运行灵活和防冻性能好等优点，目前已被越来越多的国家认同和使用。背压作为直接空冷机组中极其重要的参数变量[1]，能否实现稳定控制对直接空冷机组经济安全运行有着重要影响，所以对直接空冷机组背压控制系统进行动态特性分析和模型辨识为今后自动控制策略的设计和优化奠定了基础。

空冷凝汽器作为直接空冷机组最重要的组成部分，因其具有非线性、时变、多变量以及大迟延的复杂特性[2]，而成为众多学者的研究热点。但是，有关直接空冷机组背压控制系统模型辨识方面的文献较少，文献[3]通过空冷仿真机得到背压阶跃响应曲线，建立了背压控制系统模型，但是没有结合现场实际运行数据进行建模；文献[4]等通过借助热力学的理论知识建立空冷系统换热过程和空冷风机的机理模型，但对于背压控制系统的模型还有待确定；文献[5]通过对直接空冷凝汽器背压的主要影响因素进行分析，得出空冷凝汽器背压的模型，但是缺乏更多的数据去验证模型的精确性。本文以某300 MW直接空冷凝汽器为研究对象，设计自适应权重的PSO优化算法实现对背压控制系统数学模型的建立，对直接空冷系统对象模型的辨识以及自动控制策略的优化等方面具有一定参考价值。

1 粒子群算法辨识原理

1.1 标准粒子群算法

标准粒子群算法是在基本粒子群算法的基础上加入了惯性权重，这是一种早期对基本粒子群算法的改进方法，同时也启发了后来的学者研究和改造粒子群优化机制[6]。基本粒子群算法的粒子速度更新公式如下：

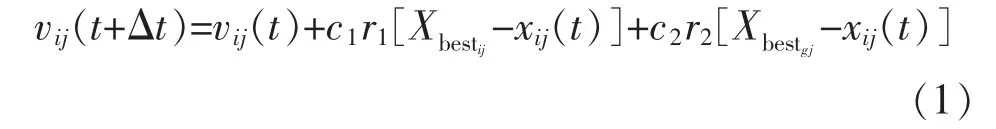
标准粒子群算法是在上式的基础上引入了惯性权重ω，如下：

式中：i=1，2，…，m；j=1，2，…，N；t为当前位置时刻；t+Δt为粒子前进一步后的时刻；r1，r2为 0～1 之间的随机数；c1，c2为加速权值。

惯性权重ω的引入是要解决全局搜索和局部搜索不平衡的问题[7]，惯性权重ω表示了原有速度在下一步中所占的比重大小，ω越大，表示受上一步速度影响越大，全局搜索能力越强；ω越小，表示受上一步速度影响越小，局部搜索能力越强。合适的ω值在搜索速度和搜索精度方面起着协调作用。所以，常采取使惯性权重ω逐步递减的方法，在粒子群算法搜索初期选取较大的惯性权重值ω，有利于实现全局搜索，在搜索后期选取较小的惯性权重值ω，有利于算法的收敛。惯性权重递减公式如下：

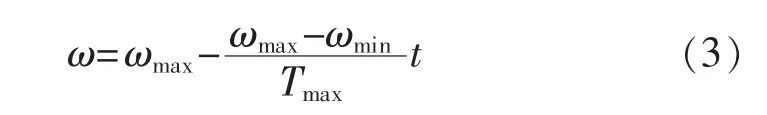
式中：ωmax，ωmin分别为ω的最大值和最小值，ω的取值范围通常在0.8～1.2之间；Tmax，t分别是最大的前进步数和当前已走过的步数。

1.2 基于自适应权重的PSO算法

粒子群优化算法中的惯性权重ω决定了粒子上一时刻的速度对当前时刻速度的影响程度，采用惯性权重ω逐步递减的方法存在一定的缺陷，它需要通过不断试验来获取惯性权重ω的最小值、最大值和迭代次数，而且很难找到能够适用于普遍问题的最佳值，其惯性权重的线性递减只针对某些问题有较好的优化效果[8]。

为了能够平衡、兼顾粒子群算法的全局和局部搜索效果，在标准粒子群的基础上将惯性权重ω计算方法进行改进，通过将线性递减的惯性权重值改进为自适应变化的惯性权重值，使得惯性权重值随着粒子适应度值的变化而变化，即自适应权重[9]。当粒子的适应度值收敛时，将适当增加惯性权重ω的值以增大全局搜索能力；当粒子适应度值分散时，减小惯性权重，以增加局部搜索能力；对于当前适应度值优于平均适应度值时，对应的惯性权重要取较小值以保护该粒子；而对于适应度值差于平均适应度值的粒子，其对应的惯性权重要取较大值以向较好的搜索区域靠拢[10-12]。

改进后的惯性权重值计算表达式如下：

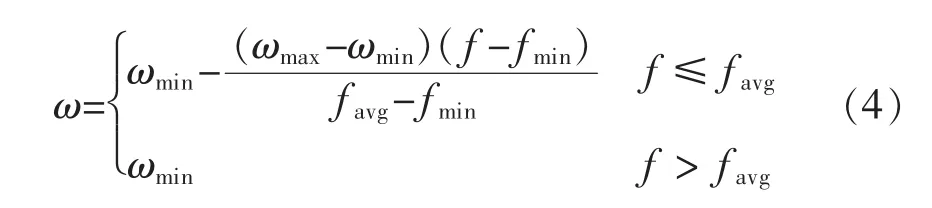
式中：f表示粒子当前的适应度值；fmin和favg分别表示所有粒子的最小适应度值和平均适应度值。

基于自适应权重的PSO算法流程如图1所示。

利用自适应权重的PSO算法来解决控制系统模型辨识问题，步骤可总结如下：

步骤1设置粒子群优化算法中一些参数的取值，如粒子群规模S，迭代次数MaxGen，粒子速度V的取值，种群维数D，辨识参数范围，惯性权重ωmax和ωmin，加速度权值c1和c2等算法中用到的常量；

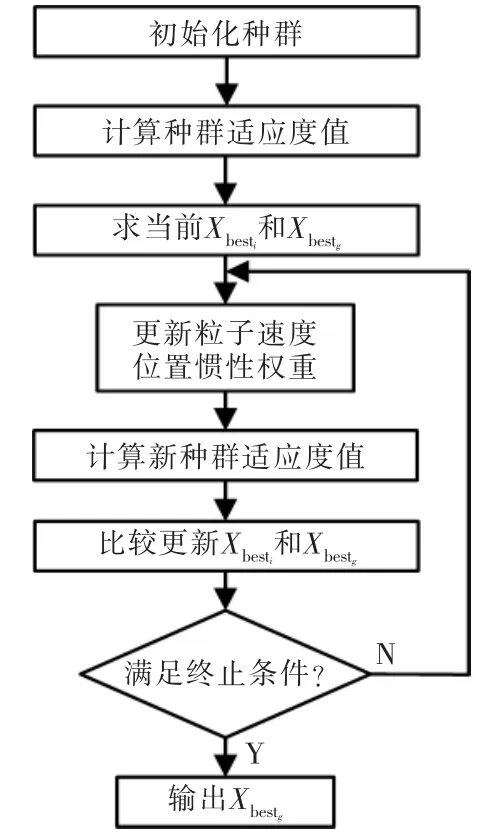
图1 基于自适应权重的PSO算法流程Fig.1 PSO algorithm flow chart based on adaptive weight

步骤2将粒子依次赋值给系统所需要辨识的模型参数，如系统开环增益K，系统惯性时间常数T1、T2，系统纯迟延时间常数 τ；

步骤3将模型参数进行赋值后，对此模型作阶跃扰动，得出阶跃响应曲线；

步骤4将此阶跃响应曲线转化为与现场试验数据采样周期一致的离散点；

步骤5求取阶跃响应曲线转化为离散点后的数值，并计算出与现场试验数据之间的偏差量e，最终得到该偏差的ITAE性能指标函数值。

步骤6判断是否满足终止条件，如果满足退出迭代循环，输出最优粒子值；如果不满足，更新粒子群以及相应惯性权重，返回步骤2继续寻优，直至满足终止条件或到达最大迭代次数为止。

2 背压控制系统

2.1 背压控制系统介绍

直接空冷系统的背压被认为是汽轮机低压缸的排汽压力，忽略了排汽由汽轮机出口流向凝汽器入口以及蒸汽在凝汽器内的流动压降。背压的主要影响因素有风机频率，机组负荷和环境温度，而调节背压的主要手段是改变风机频率，当风机频率发生变化时，因流经空冷凝汽器翅片管束的冷却介质总量发生变化，空冷凝汽器被冷却的蒸汽量也发生改变，背压随之得到调节。通过对实际运行情况的分析与研究，在某一环境温度下，当机组负荷一定时，随着风机频率增加，汽轮机背压降低，风机频率降低，汽轮机背压升高。

2.2 背压控制系统模型

对象模型的选择是系统建模工作中的重要一步，也是决定控制系统模型质量的关键性一步，控制系统模型辨识的过程实际是函数拟合的过程，包括背压传递函数模型的参数和结构。所以需要对模型的参数和结构进行优化。假设在时间域内，系统输入与输出的关系如下：

另t=KTs，其中K=1，2，…，M，Ts为采样周期，M为采样点数，带入上式有：

当测得实际系统的M组输入输出数据u（KTs）和y（KTs）时，如何估计一个能达到合理匹配的已知函数，使采集到的数据满足：

fg即为所求的系统模型，它在一定精度可以代表系统的真实模型f。

估计模型fg是在系统输入输出确定的条件下的数学模型，而实际的热工过程往往有很多难以精确描述的影响因素，所以，输入输出的实际测量数据不可能完全满足上式，实际系统的估计模型如下：

式中：e（KTs）为残差。

显然，残差e（KTs）与估计模型fg的参数有关，对参数有不同的估计就会产生不同的残差。所以无论用什么方法对模型参数进行估计，都是需要残差e（KTs）的绝对值最小，即e（KTs）趋于零。

此时，就把传递函数模型优化问题转化成传递函数参数优化问题，如图2所示。

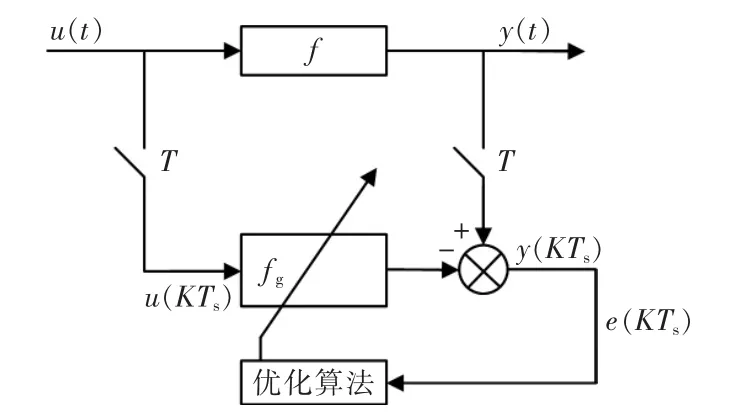
图2 辨识系统结构框Fig.2 Identification system block diagram

确定模型结构首先需要有被控对象的先验知识，以实现所建对象模型能满足较高精度的模型要求[13-15]。对于过程生产系统来说，根据专家经验，对象模型结构往往用一阶或二阶惯性时滞环节就可以描述被控对象的动态特性，在实际应用过程中，绝大多数的热工对象都具有自平衡能力，并且属于多阶惯性环节。因此，为了更好地描述背压控制系统的细节，本文采用带有纯迟延的二阶惯性环节作为背压控制系统待定模型的传递函数，具体形式如下：

式中：K为系统开环增益；T1，T2为系统惯性时间常数；τ为系统纯迟延时间常数。

因此，只要能够通过现场运行数据辨识出上述4个参数，就能得到系统模型，即把传递函数模型优化问题转化成传递函数参数优化问题。

3 基于现场数据的模型辨识

假定在现场试验时间段内，负荷和环境温度等参数不变，那么可近似认为背压仅仅由空冷风机转速决定，为此，在不同稳定负荷下，通过改变风机转速，就可间接得到背压的响应变化曲线。

3.1 现场试验及数据处理

以试验机组为研究对象，在260 MW稳定负荷工况下，在原稳定风机转速的基础上加入一定的转速阶跃扰动量，记录达到新稳定状态过程中背压的变化。

通过现场试验获取数据以后，首先对采样数据中的一些粗大值进行剔除，然后再进行零初始值处理。因实际采集的未经处理的输入输出数据u（k）和y（k）的零点可能是任意的，所以需要找到零点并剔除。零初始值后的数据如下：

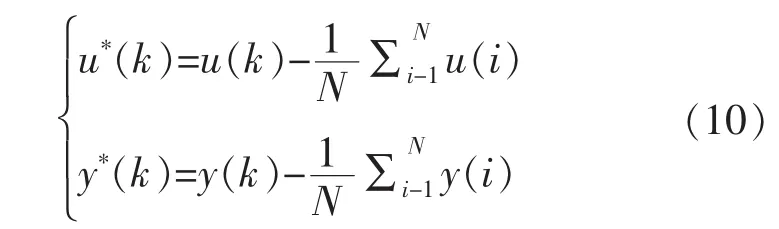
对数据进行处理后，得到背压在加入扰动前后的变化量如图3所示。

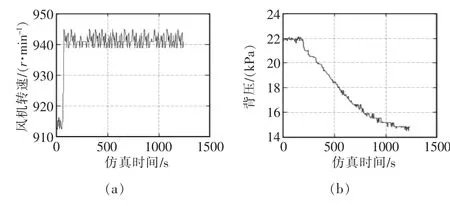
图3 现场数据及数据处理后的曲线Fig.3 Curve of field data and data processing

3.2 基于改进的PSO算法模型辨识

参数辨识方法采用基于自适应权重的PSO寻优算法，结合选取的背压控制系统对象模型，利用Matlab软件编写寻优算法主程序和性能指标子程序。以山西某矸石电厂260 MW稳定负荷工况为例进行模型辨识。辨识参数设置见表1。

表1 辨识参数设置Tab.1 Identification parameter settings

运行Matlab程序，经过60次的迭代后，待辨识参数优化曲线、适应值收敛曲线、背压控制系统辨识模型阶跃响应曲线如图4～图6所示。

获得的优化参数和辨识模型见表2。

3.3 模型验证

图4 待辨识参数优化曲线Fig.4 Optimized curve of parameters to be identified

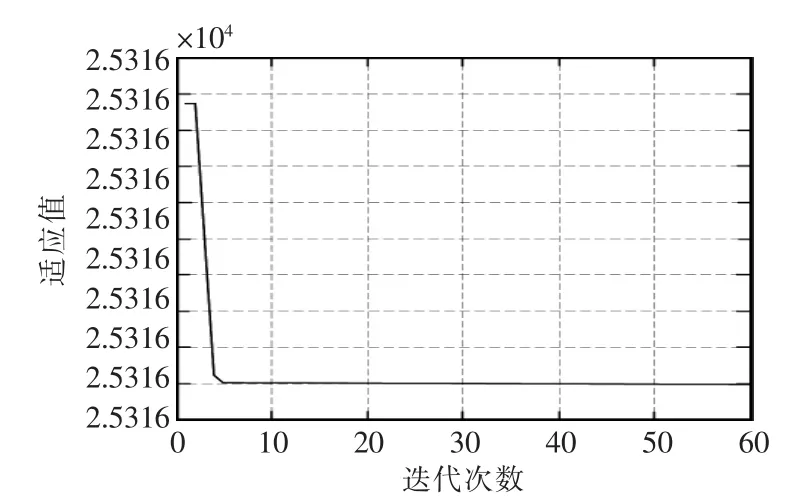
图5 适应值收敛曲线Fig.5 Adaptation value convergence curve

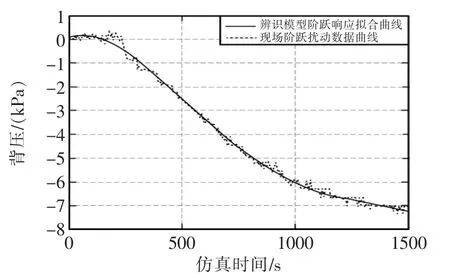
图6 背压控制系统辨识模型阶跃响应曲线Fig.6 Step response curve of identification model of back pressure control system

表2 260 MW工况下背压控制系统模型辨识结果Tab.2 Model identification results of back pressure control system under 260 MW conditions

为了验证模型的准确性和实用性，另外选取其他时间段的50组现场运行数据代入已求得的模型中，验证结果如图7所示。

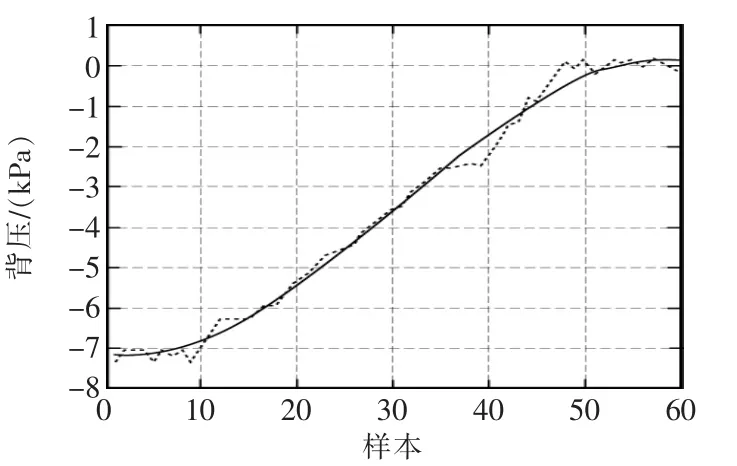
图7 辨识模型的验证Fig.7 Verification of identification model

验证结果表明，基于改进的PSO算法辨识出模型的阶跃响应曲线能很好的表征背压控制系统的实际动态特性，由图7可见，辨识模型的输出曲线与现场实际的输出曲线吻合程度较好，辨识误差值在±1 kPa范围之内，证明所建立的背压控制系统对象模型是准确可靠的，可以用于控制系统设计与仿真。

4 结语

本文通过采集某矸石电厂300 MW直接空冷机组背压控制系统的现场运行数据，并进行数据预处理，根据热工过程确定背压控制系统对象模型结构，采用基于自适应权重的PSO优化算法辨识出对象模型参数，最后另取其他时间段的运行数据验证所建模型的实用性。结果表明基于改进的PSO算法在系统模型参数辨识方面可以达到很好的辨识效果，为热工过程复杂控制对象模型的建立提供了方法指导，具有一定的借鉴意义。