一维下料问题的一种混合启发式算法
管卫利,龚 击,薛焕堂
1 引言
下料问题广泛的出现在机械制造业的生产过程中,其实质是对有限资源进行合理安排使得资源利用率最高[1-2]。一维下料问题是指:将库存线材原料切割成若干种所需零件,每种零件具有特定的长度和需求量,寻求一种下料方案使得线材利用率最高。管材,型材,棒材的切割下料均属于一维下料问题。下料方案由多种切割方式按照一定数量组合而成,切割方式是指零件在单根线材上的排列方式。目前一维下料问题的解决方法可分为两大类:以切割方式为导向的方法和以零件为导向的方法[3]。以切割方式为导向的方法首先组合零件形成多种不同的切割方式,然后确定每种切割方式所使用的数量。文献[4]针对一维下料问题提出了一种基于遗传算法的随机搜索模型,通过在可行的切割方式集合中进行迭代搜索来产生下料方案。文献[5]提出了一种顺序启发式算法,首先求出所有可行的切割方式,然后按照一定的启发式规则搜索所有可能的切割方式组合,选择一组最优切割方式形成下料方案。
以零件为导向的方法按顺序生成下料方案中各切割方式,每个切割方式满足部分零件需求量,直到所有零件需求量得到满足后终止切割方式的生成。文献[6]提出了一种基于多级序列思想的下料算法,将下料问题转化为多级序列优化问题,每级对应单根线材切割方式的求解问题,用剩余零件需求量构造每级最优序列。文献[7]提出了一种顺序价值修正算法,该算法通过顺序产生切割方式来构造下料方案,每次产生切割方式后对剩余零件的价值进行修正。文献[8]提出了AB分类算法,该算法将贪心算法和随机搜索技术相结合,每次取一根线材随机的满足部分剩余零件需求量,重复该过程直到所有零件需求得到满足为止;对可行的切割方式的材料利用率设置一个阈值,高于阈值的切割方式归为A类其余归为B类,对B类切割方式所对应的线材重新考察其切割方式直到无法产生A类切割方式或线材利用率达到理论上限为止。
这里提出一种以零件为导向的混合启发式下料算法来求解一维下料问题。该算法通过废料长度、零件平均长度、大零件数量指标来评价各个切割方式的质量;在选择切割方式形成下料方案过程中,综合考虑零件的剩余需求量、线材的库存量以及切割方式对应线材的长度。编程实现这种算法,将该算法与文献中下料算法进行测试比较,实验结果表明该算法相当有效。
2 问题的数学模型
所用到的符号(变量)及其含义,如表1所示。

表1 符号及其含义Tab.1 Symbols and Their Meanings
一维下料问题:用m种线材切割出n种零件,其中第i(i=1,…,m)种线材的长度为Li,供应量为bi,第j(j=1,…,n)种零件长度为lj,需求量为dj;约束条件为每种线材的使用量不超过其供应量,每种零件的需求量得到满足;优化目标为最大化化线材利用率。
设一维下料问题的解(下料方案)为A=[A1,…,AK],共K种切割方式,每种切割方式AK=[ak1,…,akn],其中akj表示第k种切割方式包含第j种零件的数量;第k种切割方式的使用数量为xk,对应线材的编号为 g(k)∈[1,…,m]。综上,一维下料问题的数学模型[9]如下:

上述模型,式(1)是目标函数,实现线材利用率最大化;式(2)为零件需求量约束,即每种零件的需求量都得到精确满足;式(3)为切割方式约束,即每种切割方式中的零件总长度不大于所对应线材的长度;式(4)为线材使用量约束,即每种线材所使用的数量不超过其供应量;式(5)为变量的取值范围约束,即每种切割方式的使用次数只能取非负整数。
3 求解方法
文中混合启发式算法的主要思想为用当前毛坯的需求量和线材供应量来构造一系列可能的切割方式,按优先级递减原则选择废料最少、零件平均长度最大、大零件最多的切割方式切割线材满足部分零件需求;重复上述过程直到所有零件需求量均得到满足为止。
(1)输入m种线材的数据(Li,bi),n种零件的数据(li,di)。
(2)将n种零件按照长度递减排序,得到新的零件集合E={(l1,d1),…,(li,di),…,(ln,dn)},即对于任意i∈{1,…,n},有li≥li+1。
(3)依据零件的需求量分别考察每种线材所对应的可能切割方式,按照废料最小原则确定最优切割方式。
①对于每种切割方式,通过以下递归公式计算其包含每种零件的数量:

式中:“[·]”为向下取整数符号 k∈{1,…,K},j∈{1,…,n}。
第k种切割方式其废料长度为:

第k种切割方式其使用数量为:

第k种切割方式的零件平均长度为:

②通过下述优先级原则在m种线材所对应的所有可能的切割方式集合中选取当前最优切割方式k0,优先级从(1~3)依次递减。
(1)废料长度 Wk最小,即 Wk0=min(Wk)。(2)零件平均长度 fk最大,即 fk0=max(fk)。(3)包含大零件的数量最多。
③记录当前最优切割方式以及其对应的线材长度,按照当前零件的剩余需求量和线材的剩余供应量确定切割方式使用的次数。
④更新当前零件剩余需求量和线材剩余供应量。
(4)判断每种零件的剩余需求量是否全为0,若否,则转(3),若是,则结束算法。
4 实验计算
为了检验这里混合启发式算法的性能,用C++语言实现该算法,在Microsoft Visual Studio 2010旗舰版开发平台进行实验,所用硬件环境为主频3.3GHz,内存2GB微型计算机。分别考虑单种线材下料情形和多种线材下料情形。采用文献中已有例题,将这里算法计算结果分别与文献[6]启发式多级序列线性优化算法、文献[5]顺序启发式算法、文献[8]AB分类算法、文献[10]演化算法进行比较。
4.1 单种线材下料的情形
例1:采用文献[5]例题1数据,用长度为3m的线材切割出5种零件,零件长度和需求量分别为(2.2m,5)、(1.8m,3)(1.2m,4)、(0.5m,6)、(0.3m,6),其中(2.2m,5)表示 2.2m 的零件需求量为 5个。求最优下料方案(不考虑线材切口损失)[5]。表2给出了文献[6]启发式多级序列线性优化算法求得的下料方案,表中第1行数据表示,切割方式1包含2号零件1个,5号零件4个,余料长度为0,按照该方式切割1根线材。表3给出了文献[5]顺序启发式算法求得的下料方案。这里算法求得的下料方案如表4所示,所用计算时间为0.326s,三种算法的下料方案均耗费8根线材,但这里算法前7根线材利用率达到100%,最后一根线材余料为2.4m,可供以后下料使用。文献[5-6]算法下料方案产生的余料分别分散在4根线材和2根线材中,余料种类多且尺寸较短不便于今后下料使用。因此这里算法在余料控制方面优于文献[5-6]算法。

表2 文献[6]算法计算结果Tab.2 The Calculation Result of Literature[6]Algorithm
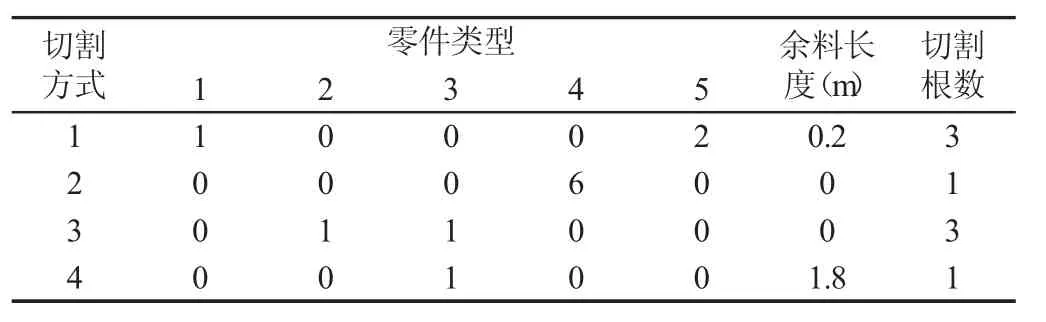
表3 文献[5]算法计算结果Tab.3 The Calculation Result of Literature[5]Algorithm
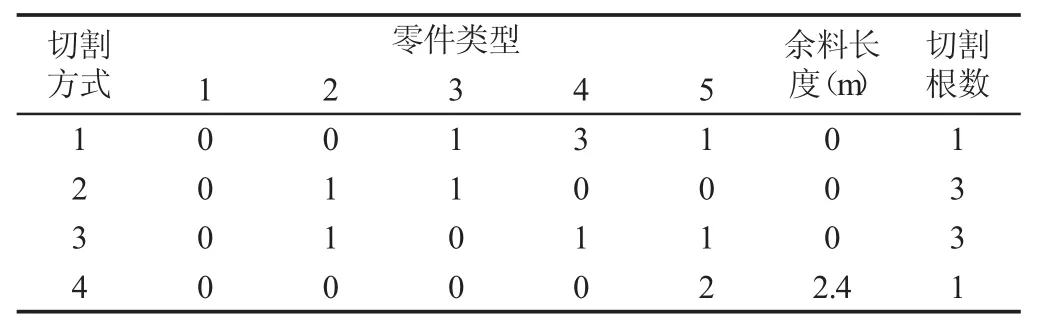
表4 这里算法计算结果Tab.4 The Calculation Result of this Algorithm
例2:采用文献[5]例题2数据,用长度为1000m的线材切割出5种零件,零件长度和需求量分别为(512m,5)、(321m,12)、(128m,8)、(247m,22)、(290m,6)。这里算法求得的下料方案,如表5所示。共耗费15根线材,材料利用率为97.40%,所用计算时间为0.409s。文献[5、8]算法求得的下料方案分别参见文献[5]的表3-6和表3-7,耗费线材分别为17根、16根,材料利用率分别为85.90%、91.30%。可见这里算法下料利用率高于文献[5、8]算法。
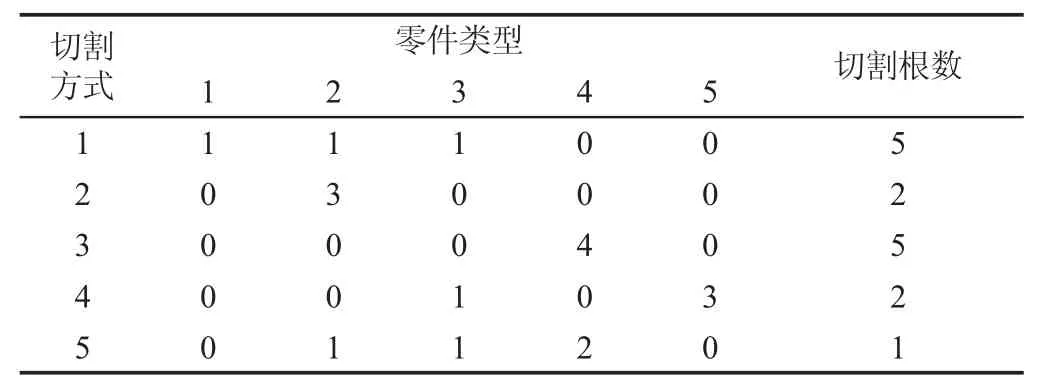
表5 这里算法求得的例题2的下料方案Tab.5 The Cutting Plan of Instances 2 Solved by this Algorithm
4.2 多种线材下料的情形
例题3:用5种线材原料切割出4种零件,线材长度分别为:320m,340m,360m,380m,400m,可用根数分为 30,40,50,40,30;零件长度分别为 35m,52m,71m,97m,需求量分别为 100,80,50,100。文献[10]VEA算法和文献[5]顺序启发式算法求得的下料方案分别参见文献[5]的表3-8和表3-12,两种算法下料方案耗费的原材料长度均为21200m。这里算法求得的下料方案,如表6所示,耗费的线材长度为20960m,所用计算时间为0.631s。可见这里算法的节材效果优于文献[5、10]算法。
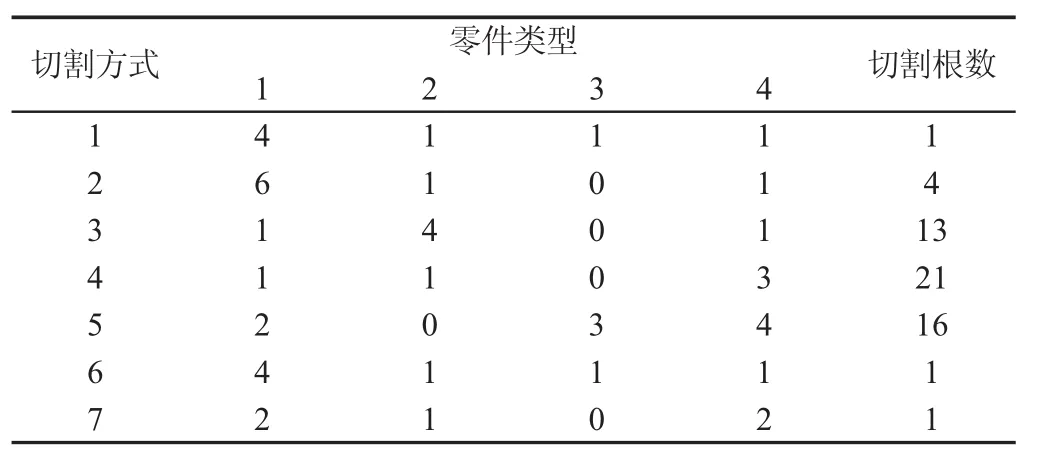
表6 这里算法求得的例题3的下料方案Tab.6 The Cutting Plan of Instances 3 Solved by this Algorithm
5 结论
建立了线材一维下料问题的数学模型,构造了解决该问题的混合启发式算法,该算法在生成切割方式时综合考虑了切割方式的废料长度,零件的平均尺寸,大零件的选取情况。克服了传统顺序启发式算法的贪婪性,即先生成的切割方式材料利用率高,后生成的切割方式材料利用率低的弊端。通过与4种文献算法进行比较,表明了这里混合启发式算法在余料控制和提高下料方案的材料利用率方面均有效,并且算法计算时间较短,能够满足实际应用需要。

