针对钛雷炮炸膛现象的数值模拟及优化

饶 刚，郭强舟，曾 越，张登辉

1 引言

钛雷驱鸟炮因其结构简单，环保且使用效率高的特性而在无伤驱鸟领域慢慢普及。钛镭炮在工作过程中主要由控制系统通过电子雷管进行引爆，在钛雷炮管中完成对炮弹的推送，炮弹抵达高空后发生二次爆炸，利用爆炸的声波来达到高空驱鸟的目的。

据使用者观察，在钛雷炮的使用过程当中时常发生炮弹推送受阻导致的二次爆炸发生在炮筒内的炸膛现象。炸膛现象发生容易诱发不同层级的事故，轻则导致设备产生结构性的损坏，影响设备使用寿命，提高投入成本，降低工作效率，重则造成操作人员受伤。观察发现，产生炸膛现象的诱因复杂，包括炮弹保管不善出现涨壳，炮筒连发过多炮管变软，炮筒内出现异物，炮膛磨损过大等都会导致炸膛的发生，故难以彻底杜绝炸膛的现象。只有从设备上去进行完善，根据有效的理论依据来进行结构上的优化与加强，以此来降低乃至抵消炮管炸膛引起的危害。

结构上的优化需要借由直接与炸膛瞬间相关的诸多数据来完成，但由于炸膛发生到结束的持续时间过短且整个过程具有相当高的危险性，难以选择安全有效的传感器进行实地测量，故选择用数值模拟的方法将炸膛过程在计算机上进行呈现并提取优化结构所需要的数据。

在进行数值模拟的过程中需要注意的是爆炸过程时间短且物质反应剧烈，为了避免爆炸带来的冲击波引起巨大的网格畸变，同时也为了减小数值模拟结果与实际情况的误差并得到收敛的解，以流固耦合的方式对研究对象进行有限元建模，并采用ALE的求解模式作为本次课题的描述方法。相对于纯拉格朗日方法和纯欧拉方法，此方法的计算网格可以独立于物质构型和空间构型运动，更有利于爆炸过程的描述与数据的提取，克服了纯拉格朗日方法和纯欧拉方法的缺陷[2]。

在针对炸膛现象建立数学模型进行理论分析时需要引入经典的Chapman-Jouguet理论。它将爆炸引起的爆轰波简化成一个冲击压缩断面，在该面上的化学反应瞬间完成，在其波阵面上仍然满足质量、动量和能量的守恒。

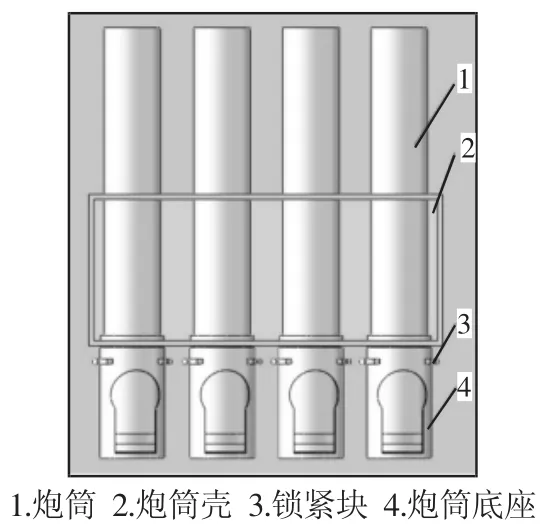
图1 钛镭炮装配示意图Fig.1 Sketch Map of Titanium Radium Cannon

2 炸膛的爆轰模型

D.L.Chapman和E.Jouguet先后提出最有效的爆轰波结构理论，后简称为C-J理论。

C-J理论假定，冲击波与化学反应区为一维间断面，其内部化学反应在一瞬间完成，化学反应速度为无穷大，反应的初态和终态重合，且流动或爆轰波的传播是定常的。该假定的特点可以描述为，一维片面波的设定可以将炸药柱的直径设想为无限大，从而忽略了起爆端的影响。将爆轰波的传播理解为冲击波的传播，化学反应区紧紧贴在冲击波的后面并当作瞬间释放能量的几何面，整个面当作一个间断面，从该面流出的物质已经处于一个热化学平衡的状态，故冲击波后可用热力学状态方程来描述。

基于此，借由三大守恒定理可以推导出如下基本方程：

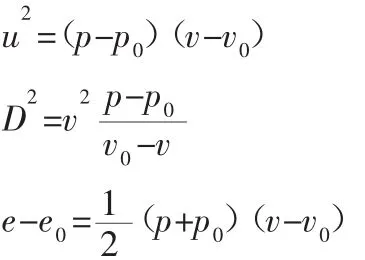
式中：p—爆轰产物的压力；v—比容（比容为密度的倒数）；e—内能；u—质点速度；D—爆轰波的传播速度，即爆速；下标“0”的表示初始状态下的相关参数。

再结合爆轰波能够定常传播的约束条件：爆轰波相对与爆轰产物传播速度等于爆轰产物的声速。可以表示为：D-u=c式中：c—爆轰产物的声速。

同时还需结合爆轰产物的状态方程描述压力与体积应变之间的关系，其具体形式为：

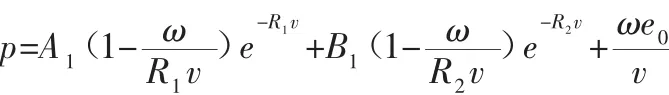
式中：A1，B1，R1，R2，ω—依据炸药的材料以及配比不同而待拟合的参数。

钛雷弹的内置炸药成分主要为黑火药，这里为方便参数上的设置采用TNT当量法，依据参考文献[3]，将黑火药的TNT当量值取为0.45。而TNT炸药的相关参数设置从参考文献[4]中获得。

整个分析模型包括后面的有限元分析采用的单位制为gcm-μs，计算所得出的压力单位为Mbar。

3 炮筒炸膛的有限元分析模型

3.1 有限元分析的前处理

考虑到炸膛现象在炮筒内发生，以炮筒单个部件进行针对性的建模和工况加载。同时考虑到炸膛现象发生的诱因不同，则炮弹发生卡壳的具体部位也不尽相同，炮弹发生爆炸的相对位置也不一样。那么，依据炸点的相对位置的不同，将具体的模拟情况细分为三个工况，分别对应的是炸点在炮筒的底端，中段以及前端的情况，具体如表1所示。

表1 数值模拟工况分类Tab.1 Classification of Numerical Simulation Conditions

在建立整个有限元模型的框架时，除了需要考虑炮筒和炮弹外，还需要纳入整个分析系统的成分是空气，空气作为充满炮筒内腔的介质，对爆炸产生的冲击波的传播有巨大的影响。将空气纳入整个有限元模型当中，完善了理论框架，同时还方便后期相关数据的提取，作用在炮筒底座上的因冲击波而产生的压力值显然与炮筒底端空气单元所承受的压力更为近似。在有限元分析软件Ls-dyna中，空气的状态方程所采用的具体形式为：

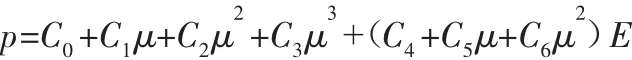
式中：C0，C1，C2，C3，C4，C5，C6—与流体属性相关的常数；E—空气的初始内能；μ=1/V，V是相对体积。空气的材料参数和状态方程均由参考文献[5]所提供。

由于炸膛是在瞬时内发生的伴有剧烈化学以及物理变化的过程，如果此时在建立有限元模型时使用纯拉格朗日方式建模难免会在剧烈的物理变化过程中致使网格发生畸变从而导致模型的计算终止而无法得到想要的解。故在模型的算法上引入流固耦合方法中的ALE表示法，此方法的优势在于，计算网格可以独立于物质构型和空间构型运动，通过合适的网格运动定义就可以准确的描述物体的移动，使单元在物质的运动过程当中保持合理的形状。此次研究的具体网格属性分配中，将描述炮筒的单元定义为拉格朗日网格，将炮弹即炸药部分定义为ALE单元。

3.2 有限元分析结果与后处理

1号工况下的数值模拟分析结果云图，如图2所示。显示炮筒在炸膛发生过程中产生的最大等效应力为6.348×10-5Mbar，换算为常用单位等于6.348MPa，其值远远小于炮筒的材料的许用应力，故炮筒部件本身并不发生致命的结构性损坏同时炮筒的动力学性能也不受影响。因此，在设置优化问题时，炮筒内壁所收的压力值在施加载荷时应当忽略不计。

图2 工况1下的炮筒应力云图Fig.2 Stress Nephogram Under Condition 1

在1号工况下，拾取炮筒底部附近的空气单元簇，提取其所受的压力值并绘制与时间关联的曲线，如图3所示。

图3工况1下的空气单元所受压力随时间变化曲线（us—10-3Mbar）Fig.3 The Change Curve of Pressure vs.Time Under Condition 1

图3 显示，在工况1中所模拟的炸膛在炮筒底端附近某单元所受到的压力值在t=250us左右时达到最高峰值，其值为3.63×10-5Mbar，并可以将其换算为3.63MPa。基于上一节理论算法计算该工况的结果为3.47MPa，两者误差为5%，故可以认为数值模拟结果有效。2号工况下的数值模拟分析结果云图，如图4所示。显示炮筒在炸膛发生过程中产生的最大等效应力为6.340×10-5Mbar，将其换算为常用单位为6.340MPa。

图4 工况2下的炮筒应力云图Fig.4 Stress Nephogram Under Condition 2

在2号工况下，拾取炮筒底部附近的空气单元簇，提取其所受的压力值并绘制与时间关联的曲线，如图5所示。

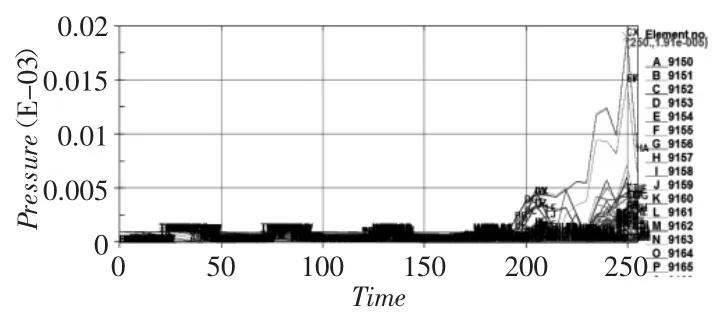
图5工况2下的空气单元所受压力随时间变化曲线（μs—10-3Mbar）Fig.5 The Change Curve of Pressure vs.Time Under Condition 2

图5 显示，在工况2中所模拟的炸膛在炮筒底端附近某单元所收到的压力值在t=250us左右时达到最高峰值，其值为1.91×10-5Mbar，并可以将其换算为1.91MPa。该工况的理论计算的结果为1.77MPa，两者间误差为8%，同样可以认为数值模拟结果是有效的。3号工况下的数值模拟分析结果云图，如图6所示。显示炮筒在炸膛发生过程中产生的最大等效应力为6.108×10-5Mbar，换算为常用单位等于6.108MPa。

图6 工况3下的炮筒应力云图Fig.6 Stress Nephogram Under Condition 3

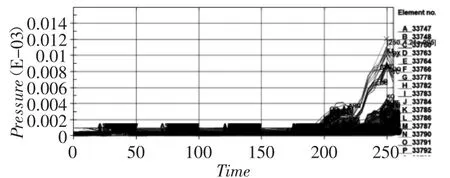
图7 工况3下的空气单元所受压力随时间变化曲线（μs—10-3Mbar）Fig.7 The Change Curve of Pressure vs.Time Under Condition 3

在3号工况下，拾取炮筒底部附近的空气单元簇，提取其所受的压力值并绘制与时间关联的曲线，如图7所示。图7在工况1中所模拟的炸膛在炮筒底端附近某单元所收到的压力值在t=250us左右时达到最高峰值，其值为1.21×10-5Mbar，并可以将其换算为1.21MPa。该工况的理论计算的结果为1.16MPa，两者间误差为4%，故同样可以认为数值模拟结果是有效的。

结合图2、图4、图6中的数值模拟结果分析，随着炸膛发生时的炸点相对于炮筒底座的距离增大，炸膛所产生的爆轰波对炮筒底座产生的压力呈衰减趋势。这基本印证了炸膛发生的实际情况，也符合爆轰理论模型的基本规律。

综合上述对三种炸膛现象的数值模拟已经可以了解在钛雷炮筒内炸膛压力的有关规律，并且数值模拟的结果与理论计算的结果相差很小。足以证明本次对钛雷炮炸膛的数值模拟是与经典爆轰模型相结合的有效理论实践，而且从中所提取的数据将为后来的优化问题设置提供参考。

4 炮筒及其紧固件的优化

此次优化的目的是，当炸膛现象发生时，钛雷炮装配体不发生明显结构损坏。根据实际操作经验，在炸膛现象发生时容易发生结构性损坏或原有装配体系被破坏的相关部件已在图1中有所展示，面对此问题，针对图1中的主要部件建立相关的数学模型。

4.1 优化目标

目前，与钛镭炮有关的制造工艺已经比较纯熟，故在优化过程中与工艺相关的制造成本不必考虑。这就意味着炮筒相关装配体的质量越小，材料成本也会越低。那么，在同时满足刚度、强度等要求的前提下，炮筒相关装配体的质量越小，其表现出的疲劳寿命也就会越高。基于此，提出以整个装配体的质量最小建立优化的目标函数：F（X）=min（m）式中：m—装配体质量。

4.2 载荷的确定

基于有限元分析结果，已经可以确定直接面向优化问题时的载荷。在所模拟的三种工况中选取炮筒底座所受压力的最大值作为此次优化问题的载荷值以确保任何诱因下发生的炸膛均不会导致钛雷炮装配体的结构性损坏。故取载荷值为P=3.63MPa。

4.3 设计变量

为了能在解决问题的前提下对原有结构进行尽可能小的改动，故提出以锁紧块的厚度，炮筒底座的厚度，以及锁紧块的嵌入深度作为设计变量。

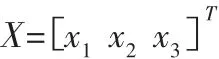
依据装配体中各个部件的空间位置关系等约束条件和制造工艺的要求进行了相应的波动比例限制。其具体数值、各变量的含义以及初始值，如表2所示。

表2 优化设计变量Tab.2 Optimal Design Variables

4.4 约束条件

为保证在炸膛发生时钛镭炮的各个部件不发生不可逆转的结构损坏，其强度是首先要考虑的因素。由于钛镭炮是由单一金属材料制作而成，其力学性能表现为各向同性，故引入经典的Von-Mises准则作为强度约束条件，钛镭炮筒及其相关紧固件的主要材料为Q235-A，此时依据钛镭炮的使用规范放大安全系数为2可得材料许用应力［σ］=117.5MPa。

依据实际操作经验，当炸膛现象发生时，炮筒底座与炮筒发生脱钩是出现频率最高的结构损害问题，在炮筒与炮筒底座间起连接作用的炮筒弹簧端部发生巨大变形。在正常情况下炮筒弹簧两端的弯折角度为90°，经过长期的统计与观察，炸膛现象发生后，炮筒弹簧的弯折角度有明显减小，其数值往往在（20～70）°之间，弯折程度改变量在（70～20）°的范围内，故在此假设炮筒弹簧的极限弯折程度改变量为20°，弯折改变量大于20°以后将其视为失效。结合炮筒紧固件的连接孔尺寸以及相关的平面几何算法，将其换算为炮筒底座沿炮筒的轴向位移d有：

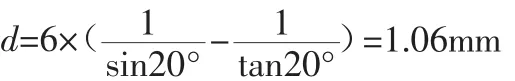
故可得炮筒底座的位移约束条件为：dmax≤d＝1.06mm

至此整个优化对象的数学模型得以建立，导入至有限元软件optistruct进行优化计算。

4.5 优化结果

基于上述优化方案，在满足强度要求以及最大位移约束的条件下，在进行到第24次左右的迭代计算时，其计算结果已经趋于稳定，优化过程已达收敛。具体结果与初始值的比较，如表3所示。

表3 设计变量的优化结果Tab.3 Optimization Results of Design Variables

以表3中的优化结果为基础，对部件尺寸做出合理圆整，按照优化数据进行制造与再装配，装配完成后的实物，如图8所示。

图8 优化后再装配的钛雷炮实物Fig.8 Optimizedin Kind

5 钛雷炮炸膛对比试验

试验内容为，将再装配完成后的钛雷炮整体置于室外空旷处，环境温度为25℃，在无风条件下进行。将剪除一级引线的钛雷弹在炮筒内引燃，炸点与炮筒的相对位置分别为距炮筒底座底面距离为2mm、20mm、40mm。

在不同炸点分别进行10次引爆试验以后均未出现炮筒底座脱钩的现象，其中有3次在引爆后炮筒壳产生了较为明显的震荡，2次出现了锁紧块在引爆后有略微松动的情况，其余的引爆试验中优化后的设备都呈现出相当可靠的安全性能。在所有的引爆试验当中均未发生不可逆的结构损坏，相较于未优化前的结构损坏已经大大降低乃至抵消，优化后的钛雷炮在炸膛发生后只需做简单清理就可以再次投入使用，不再出现以往零部件报废的情况。故可以认为此次针对炮筒及其紧固件的优化方案是有效的。

6 结论

通过数值模拟的形式成功确定了在炸膛现象发生时钛雷炮所受的冲击波载荷，并在设置优化问题时将其转换为压力载荷。该过程中可得到如下的结论：（1）利用流固耦合方法对剧烈的爆轰现象进行数值模拟能够准确拾取冲击波载荷，为后来设置优化问题提供了有效的载荷数据。（2）得到了炸膛产生的爆轰波对炮筒底座产生的压力随时间变化的数据曲线，进一步掌握了针对该模型而言的压力变化规律。

基于所取得的数据，有效设置优化问题并进行求解，得到优化后的方案并进行加工与再装配。新装配体在炸膛模拟试验中表明本课题中的优化方案基本解决了炸膛现象引起的炮筒底座脱钩问题。