基于云模型的仿真可信度评估方法

郑垚宇，方洋旺，魏贤智，陈少华，高 翔，王宏柯，彭维仕

(1.空军工程大学航空航天工程学院，西安710038; 2.95889部队武器系统与运用工程部，甘肃酒泉735018)(*通信作者电子邮箱1694654773@qq.com)

0 引言

仿真可信度评估可以提高仿真系统的质量，增加仿真系统的认可程度。它作为一个定量概念，是指仿真用户在一定需求下对于特定仿真系统及其仿真结果是否正确的信任程度［1］。在实际的仿真可信度评估时:一种方法是根据系统结果和数据特征计算得出近似的评估结果;另一种方法是由相关专家给出评估值，但是由于被评估对象的模糊性和评估人员认识的局限性导致评估人员很难给出精确的评估值，因此仿真可信度评估研究需要针对主观和客观划分、定性和定量转化两个方面展开。

结合概率理论和模糊数学提出的云模型，利用云模型发生器算法实现了定性和定量有效转换。该模型可以很好地解决评估过程中模糊性和随机性，已在环境［2］、决策［3］、军事［4］和通信［5］等领域广泛应用，但应用到复杂仿真系统可信度评估的研究较少，尤其是底层指标的评估值的获取较为简单。在以往的云模型发生器算法中，一般都是利用正态云模型进行定性定量转换［6］，然而实际仿真系统被评估对象服从均匀分布、幂率分布和泊松分布等非正态分布，现有的正态云模型发生器尚不能处理此类数据信息。本文首先对基于均匀分布的逆向云算法进行理论推导，并设计实验对其进行有效性验证，最后将其用于仿真系统的可信度评估，实现了仿真可信度的有效评估。

1 云模型理论

定义1 设U是一个用精确数值表示的定量论域，C是U上的定性概念，若定量值x∈U，且x是定性概念C的一次随机实现，x对C的确定度μ(x)∈［0，1］是有稳定倾向的随机数，则x在论域U上的分布称为云，每一个x称为一个云滴［7］。

云模型的三个数字特征分别为期望Ex、熵En和超熵He，它们以精确数值的形式表征定量概念。期望Ex为评估数据在评估空间内的期望，评估数据与Ex越接近，则与群体意见的一致性越高。评估值与Ex差值越小，云滴越集中，反映专家评估意见越统一;评估值与Ex差值越大，云滴越分散，反映专家评估意见越分散，此次评估的结果的可信任程度将受到质疑。熵En为评估数据分散程度的表征，它一方面体现评估数据的随机程度，体现了评估数据的模糊性;另一方面也体现该组评估数据被接受的区间范围，体现了评估数据的模糊性。熵的取值越大，则评估数据的随机程度和模糊程度就越高，评估意见就越不统一，反之亦然。超熵He为评估数据凝聚度的表征，它是熵的分散程度的度量，体现评估数据在评估区间内的不同群体的凝聚特性，超熵的大小在云模型中反映云的厚度。

概率论以概率的形式对概念的不确定性进行描述，模糊数学以隶属度的方式来体现概念的不确定性，尽管两者的出发点和应用领域不同，但是它们表征的本质相一致。云模型以云参数的随机性和模糊性为纽带，用正向云算法和逆向云算法实现了定性和定量的转换，其理论基础还是概率论和模糊数学。

本文提出将云模型分为数据分布、云厚度分布和隶属函数三部分，主要依据数据分布和云厚度分布的不同，对基于常用概率分布函数的一维云模型算法进行研究。考虑到云模型参数(Ex，En，He)基于数据进行统计分析来确定，没有针对某种特定的分布，因此可以利用数据分布和云厚度分布的期望和方差来估计云模型参数。由于两者的数学含义具有很高的相似性，因此以云参数和分布参数作为桥梁，对云模型算法进行推导，并以云参数误差为评判准则对云模型算法的有效性进行评估，最后将其应用于仿真可信度评估。

2 可信度评估指标及方法

在仿真应用于过程实践之前对其进行仿真可信度评估，可以有效地提高仿真的准确度，减少人力和物力损失，促进对仿真精度和系统评估的进一步深入研究;同时可信度评估指标的建立是可信度评估的关键，它的建立需要考虑仿真系统的逻辑结构、属性关系、影响因素和作用机理以增加评估的有效性。

2.1 可信度评估指标构建

通过对仿真系统的深入研究，为了验证某型装备抗干扰能力评估结果可信度建立了评估结果可信度指标体系如图1所示，从仿真环境逼真度F、实验条件覆盖度C和数据融合可信度R三个方面进行评估。本文选取仿真环境逼真度F指标进行评估，它指仿真系统建模与真实战场环境相一致的程度，决定了仿真模型的可用程度，可以从数字仿真F1、半实物仿真F2和实验环境逼真度F3三个方面进行可信度评估。

图1 总体评估指标Fig.1 Overal evaluation indexes

依据该装备数字仿真的特点，将数字仿真逼真度F1分为六个方面如图2所示，分别为约束条件、数学模型、仿真流程、仿真实现、计算方法和仿真结果。

图2 数字仿真逼真度评估指标Fig.2 Evaluation indexes of digital simulation fidelity

约束条件逼真度F11，考察该装备的初始化条件、终端约束条件以及在工作过程中的相关因素的约束条件是否与实际导弹飞行系统相一致，主要考虑这些约束条件的充分性和合理性。

数学模型逼真度 F12，评估参考 VV＆A(Verification，Validation and Accreditation)标准，对数学模型初步校核、验证和确认。其中:校核是指仿真或模型是否满足开发者的设计，能否准确完整地从一种形式向另一种形式转化;验证是指仿真或模型对真实事物的复现程度，是否可以在一定误差许可范围内代表真实世界;确认是指模型或仿真对于特定功能的初步校核的过程。

仿真流程逼真度F13，指仿真过程中的仿真时序是否与实际相一致，是数字仿真的重要指标，主要从完整性和准确性两方面进行评估。

仿真实现逼真度F14，评估数字仿真对所要实现的功能任务的完成能力，主要从功能和奇值处理两个方面进行评估。功能主要从仿真设计的技术要求以及实际仿真需求进行评估，而奇值处理则从特殊值或者特殊状态的功能实现进行仿真的逼真度考核。

计算方法逼真度F15，针对数字仿真中所用的模型方法进行评估，主要从计算方法的经典性和有效性两个方面进行评估。

仿真结果逼真度F16，对仿真结果是否与实际结果相一致进行评估，可以从仿真结果的置信度和仿真结果的可比性两个方面进行评估。

2.2 基于云模型的可信度评估指标计算方法

可信度评估指标体系总体结构为递阶层次结构，底层指标和权重值的计算是可信度评估的关键。对底层指标评估时往往有定性结果和定量结果两种情况，定量结果可以直接转化为云参数，定性结果利用云模型将其转化以云参数为特征的定性结果。

对于定量结果，假设底层指标的可信度评估定量结果为r1，则将其转化为云参数(r1，0，0)。对于定性结果一般有三种情况:一种是由评估人员直接给出评估区间值［ai，bi］或评估值分布参数［μi，σi］;另一种是由评估人员选出模糊评价集(如{优，良，及格，差});最后一种是直接由专业人员给出底层指标评估值的云参数。本文主要针对第一种情况进行讨论，并且直接给出评估值区间更加符合评估人员的思维;第二种情况可以映射为第一种情况，然后转化为云参数;第三种情况可以利用综合云生成器得到结果［8］。

定性结果的量化步骤主要包括:1)确定评估人员的权重级别;2) 利用评估区间值［ai，bi］或评估值分布参数［μi，σi］按照权重比随机产生一定数量的评估值数据;3)利用逆向云算法，将随机产生的评估值数据转化为云模型参数。

权重W的计算方法采用基于云模型的权重计算方法［8］，上一层指标可信度Cup就是将下一层指标可信度云向量Rdown与权重云向量Wdown相乘，一层一层聚合得到顶层可信度，计算按式(1)进行:

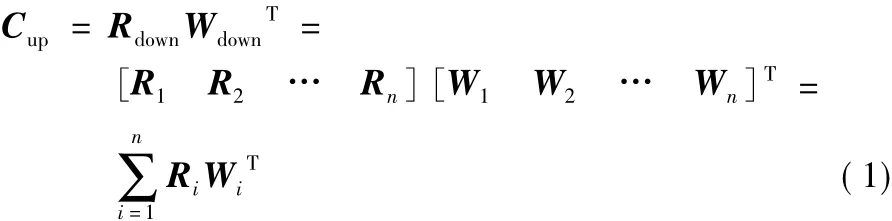
其中:Ri为第i个指标可信度云向量;Wi为第i个指标的权重云向量。

3 基于均匀分布的一维逆向云算法

仿真可信度评估首要任务就是将评估值数据转化为云模型参数，逆向云发生器可以将一系列的数据值转化成与之对应的云参数(Ex，En，He)表示定性值，以这三个数据特征表示一系列精确数据的整体，即逆向云发生器可以实现从定量值向定性特征的转化。

目前有四种逆向正态云发生器，分别为传统均值法［6］、曲线拟合法及其改进算法［6，9］、无确定度逆向云算法及其改进算法［10－11］和基于区间数的逆向云算法［12］。传统均值法以数理统计的方法估计云参数，只利用了部分x数据信息，并且在x趋近于Ex时En'→∞，由于估计过程受随机过程的影响会导致较大误差。拟合法以正态分布曲线对数据拟合获取Ex参数，属于有确定度信息，精度较高，并且在求解Ex时删除部分数据获得更高精度，He参数精度也符合要求。基于正态分布的无确定度逆向云算法不需要获取确定度信息，在一定数据量N并且舍弃部分云滴时云参数可以达到较高精度要求，但是忽略了云滴的分布规律。基于区间数的逆向云算法没有舍弃云滴信息，不需要确定度信息就可以高精度还原云参数，水平截集α的获取比较主观，并且对结果影响较大。

在实际工程应用中，可以得到比较准确的数据值，但是这些数据值的确定度无法直接得到，间接求解又会引入较大误差，因此本文选取无确定度逆向云算法作为逆向云发生器的求解算法。在实际评估过程中，数据的分布一般服从正态分布，但是还是有一些情况会服从其他常用分布，尤其均匀分布居多。本文提出将无确定度逆向云算法扩展到常用分布的思路，并以均匀分布为例进行推导和验证。

3.1 基于均匀分布的一维逆向云算法

设数据x分布服从均匀分布U1(α1，β1)，云厚度分布服从均匀分布 U2(α2，β2)，云模型参数为(Ex，En，He)。由云模型原理可知，中间参数En'服从以En为期望、He为标准差的均匀分布，下面利用中心距对云模型三个参数进行推导:

1)期望Ex为云滴定量值xi的样本均值:

2)用数据的期望和标准差作为云模型参数期望、熵和超熵的估计可得:

根据参考文献［13］可以得到x和En'的联合分布为:

令En'=y，求X的一阶绝对中心距:

结合式(3)，式(5)简化为:

3)求X的二阶中心距为:

因此熵En的计算公式为:

结合式(3)同理可得:

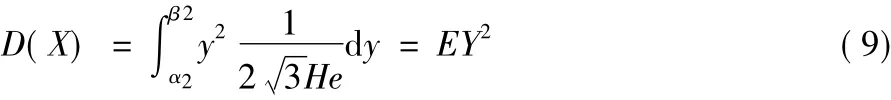
由D(X)=E(X2)－［E(X)］2可得超熵为:

利用以上求解云模型参数结论，可以得到基于均匀分布的一维逆向云算法算法步骤如下:

输入 N个云滴样本的数据值xi(i=1，2，…，N)，数据和云厚度分布为均匀分布。

输出 云模型参数(Ex，En，He)，数据分布参数(α1，β1)，云厚度分布参数(α2，β2)。

步骤1据云滴定量值xi计算样本均值珔X;

步骤5 如果S2－En2≥0，则转向步骤步骤7，否则转向步骤步骤6;

步骤6 删除当前样本中距离期望Ex最近的e=1%样本点，再转向步骤4;

步骤4 计算云滴样本方差

在基于正态分布的逆向云算法的有效性验证时，可以通过本文算法与现有算法进行比较，但是基于均匀分布的逆向云算法是第一次提出，因此设计逆向云算法的参数误差仿真实验，对该算法进行误差分析。

在实验中，以基于均匀分布的正向云算法［14］产生数据，然后利用基于均匀分布的逆向云算法求解云参数，最后对各参数误差进行分析。文献［14］的算法2中给出的均匀分布区间是人为设定的，可信度不大，可以根据式(3)计算均匀分布区间为 ［En －He，En+He］ 和［Ex －En'，Ex+En'］。设置基准值为 Ex=25，En=3，He=0.3 和 N=1000，采用控制变量的方法依次改变基准值，每个实验重复运算100次消除算法中随机误差的影响，最终得出各参数误差和各因素的影响规律，验证逆向云算法的有效性和适用性。具体各因素对云参数的影响如图3所示。

3.2 算法的有效性验证

图3 云模型参数误差Fig.3 Errors of cloud model parameters

由图3可以看出，基于均匀分布的逆向云算法可以有效地对云参数进行估计，各参数误差均在可接受范围内。各参数变化对云参数估计规律如下:均值Ex对云参数估计基本无影响;熵En＜3时误差较小，熵En＞3时随熵值增加误差明显增大;超熵He＞0.3时误差较小，超熵He＜0.3时误差较大，这和正态分布云模型规律不一致;云滴数N对均值Ex和熵En影响较小，云滴数增加时超熵He明显减小。

在逆向云算法中，对距离期望Ex的数据会进行删除，如果删除数据大于上限a%则认为此组数据有错，若删除数据小于a% 则数据可用，但是数据利用率会有影响。针对于超熵He＜0.3变化规律与实际不一致的情况，选取数据利用率和随机因素产生的错误率如图4所示。在超熵He＜0.3时，由于S与En相差不大，随机过程产生的数据不可用的概率较大，存在删除数据过多状态，对超熵的估计影响比较大。

图4 数据利用率和错误率Fig.4 Data utilization rate and error rate

4 实例分析

下面以可信度评估指标的子模块F1为例，验证基于云模型的仿真可信度评估方法的可行性和基于均匀分布的逆向云算法的有效性，评估指标体系如图2所示。

4.1 数据采集

计算方法逼真度F15是一个定性指标，可以从计算方法的经典性和有效性两个方面进行评估。本文采用基于云模型方法对其进行评估，主要选取经典性指标数据进行计算。计算方法经典性评估由8位专家给出可信度区间评估，并且每一位专家根据在评估领域水平设置一定权重，依次为0.2500、0.1667、0.1667、0.0833、0.0833、0.0833、0.0833 和0.0833。对于关键的三种计算方法，专家评估结果如表1所示。

表1 计算方法经典性专家评估值Tab.1 Expert evaluation value of calculation method canonicity

4.2 数据预处理

表1为评估人员给出的评估值区间，近似认为区间内评估值等概率均匀分布。假设需要数据总数为N，则对应于各区间的数据量按照评估人员权重等比例分配:

Ni=N*Wi(11)其中:Wi为评估人员权重;Ni为第i个评估区间需要产生的数据数量。

4.3 判定数据类型

正态分布具有普适性［15］，是很多概率分布的极限分布，广泛存在于自然现象、社会现象、科学技术以及生产活动中，在实际中遇到的许多随机现象都服从或者近似服从正态分布。但是对于可信度评估过程中评估人员较少，产生的数据有时不能用正态分布来近似，因此需要选取合适的分布尽量减小评估误差。

首先对评估数据的平率分布图进行分析，三种计算方法经典性评估值的频率分布如图5所示。

由评估数据的频率分布可以看出方法二的数据分布与正态分布相差较大，接近于均匀分布，因此选取正态分布和均匀分布的概率密度曲线拟合评估数据的频率分布，以残差平方和度量数据分布形式，计算结果如表2所示。

由残差平方和结果可知，方法一和方法三在正态分布拟合时残差平方和分别为0.003 469和0.002 814，远小于均匀分布拟合的残差平方和，因此方法一和方法三选用正态分布云模型，同理方法二选用均匀分布云模型对云参数进行估计。

图5 扩展数据频率分布Fig.5 Frequency distribution of extended data

表2 数据拟合残差平方和Tab.2 Sum of squares of data fitting residuals

4.4 计算云模型参数

利用3.1节基于均匀分布的的逆向云算法和文献［11］的逆向云算法对表1的专家评估数据进行计算，同时利用简单的加权平均方法进行求解作为对比数据，计算结果如表3所示。

表3 计算方法经典性云模型结果与加权平均值结果Tab.3 Cloud model results and weighted average results of calculation method canonicity

分析表3数据可以看出，云参数的期望与加权平均值基本一致，但是附加了评估数据的熵和超熵信息，对最终的可信度评估也有一定影响。云参数的熵值基本一致且在合理范围内，这说明评估值的分散性较好，进一步验证了评估数据的有效性。云参数的超熵比熵值低一个数量级，但是方法二的超熵较大，可能存在数据值出错的风险。进一步对方法二的原始数据频率分布进行分析如图6，可以看出评估数据分成两个相对分散的数据团，导致超熵较大，但是数据整体的熵值较小，数据相对集中，可以作为评估数据进行下一步评估。

图6 方法二原始数据频率分布Fig.6 Original data frequency distribution of the second method

同理采用上述经典性指标评估方法对有效性指标进行评估，计算结果如表4所示。由表4可以看出，云参数结果与平均值接近，表明此次评估有效，并且云参数的超熵比熵值较小，数据的分散性和凝聚性较好，表明此次评估各位专家意见统一性高，评估值可信度高。

表4 计算方法有效性云模型结果与加权平均值结果Tab.4 Cloud model results and weighted average results of the calculation method validity

4.5 评估值聚合

此处假设三种计算方法在经典性和有效性聚合时权重云参数均为(1/3，0，0)，利用式(1)对各指标的云参数进行聚合，假设各云参数为 Ri(Exi，Eni，Hei)(i=1，2，…，n)，由文献［8］得:

最终计算方法经典性指标 F151云参数为(0.825 0，0.0336，0.0163)，计算方法有效性指标 F152云参数为(0.8458，0.0375，0.0113)。在实际工程中，对图 2 中其余指标计算结果如表5、表6所示。

最终数字仿真逼真度 F1计算结果为(0.876 9，0.188 2，0.0123)，其中参数 0.876 9即为数字仿真逼真度，参数0.1882和0.0123分别从不同层次表示逼真度的不确定度。通过和传统的评估方法相比，基于云模型的可信度评估方法不仅可以准确计算数据的期望值信息，而且在聚合过程中还将评估值数据的分散度信息和凝聚度信息纳入其中，综合考虑了评估值数据的完整信息。通过设计相应软件将每一个节点的云参数数据进行输出和判断，还可以对错误数据及时剔除并作进一步更高准确度的评估。

表5 数字仿真逼真度指标评估值Tab.5 Evaluation value of digital simulation fidelity index

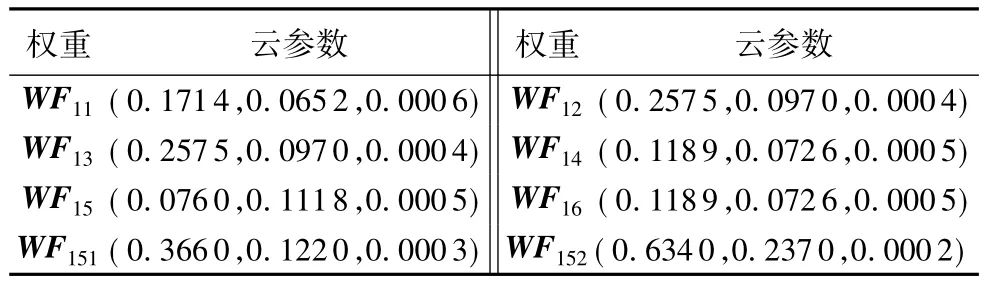
表6 数字仿真逼真度权重评估值Tab.6 Evaluation value of digital simulation fidelity weight

5 结语

仿真可信度评估是亟待深入研究的一个重要的方向，并且基于云模型的的仿真可信度评估是目前一种有效的评估方法，但是由于云模型算法的只针对正态分布有所研究的局限性，导致该评估方法的应用性不强。本文在深入研究云模型的基础上提出了基于均匀分布的逆向云模型算法，并且设计实验对算法的有效性进行了验证，实验结果表明该算法精度较高，满足工程实践要求。并且依托国家安全重大基础研究发展计划课题，建立了某型装备的可信度评估指标，提出了更加完善的基于云模型的可信度评估方法，针对数据不服从正态分布的情况，给出有效的解决方法。评估结果表明，基于云模型的仿真可信度方法可以以搞准确度进行评估，同时可以体现评估数据的分散和凝聚信息，有更高的信息利用率。综上所述本文的研究工作，不仅可以促进云模型理论的进一步完善和应用，而且对于具体装备的仿真可信度的研究也有较大的参考价值。

此外在评估过程中仍存在不完善之处需要进一步进行研究，一方面是数据分布相似度的判定需要选择更优的方法，另一方面考虑数据服从其他分布的情况，基于任意分布的逆向云算法有待研究。