基于Matlab/Simulink的小型制导炮弹六自由度运动仿真∗

强明辉 安 杨

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）

（2.兰州理工大学甘肃省工业过程先进控制重点实验室 兰州 730050）（3.兰州理工大学电气与控制工程国家级实验教学示范中心 兰州 730050）

1 引言

进入热兵器时代以来，火炮在各大小战争中都发挥着巨大的作用。而随着技术的不断进步以及战场环境日益复杂化，常规火炮的性能已不能满足现代战争对精度和射程的要求，于是，制导炮弹应运而生［1］。最近几年以来，由于军工领域加大了对高性能动力装置和精准制导技术的科研力度，使得制导炮弹的研究重点已经不再局限于传统性能方面，而是侧重于新型炮弹的研究，目前已是多国研究的热门课题［2］。制导炮弹是一种典型的综合性复杂系统，其表现在结构的复杂性和描述的复杂性［3］。现今各国巡航导弹制导技术已相当成熟，其原理是将景象匹配应用在导引头。它是指将两幅在不同时间或其他不同的环境条件下拍摄到的图像进行匹配，以确定两者在位置或属性上的差异，从而进行精确打击目标［4～5］。然而制导炮弹却不能采用图像匹配技术，原因有以下三点：首先制导炮弹短射程近滞空时间短，无法满足图像匹配所需的时间；其次是所需的成本过高；最后是无法满足制导炮弹设备的小型化［6］。

2010年美国陆军开始启动了XM395精确制导迫击炮弹的研究，简称PGMM项目。这款制导炮弹采用了GPS和半主动激光末制导技术，弹道修正采用脉冲发动机实现，其射程可达7.2km，CEP可达1m［7］。该精确制导迫弹的制导原理为：在迫击炮弹飞行末段，地面作战人员通过一个激光照射器照射需要精确打击的目标，目标反射回来的激光由安装在弹体上的激光导引头接收，炮弹通过反射回来的信息，确定目标的位置信息和GPS得到的炮弹位置信息，计算出落点与目标的误差，通过启动脉冲发动机产生不同方向的推力来调整弹道，以达到精确打击激光照射目标的作战目的［8～9］。

近年来研究者们提出采用“系数冻结”法建立自旋制导炮弹弹体扰动运动数学模型。因为弹体绕纵轴的滚转运动使制导炮弹的运动变的复杂，使其动力学呈现了复杂的非线性特点，呈现了较强的耦合特性［10］。为了使制导炮弹能够实现远程精确打击、高效毁伤等优势，制导炮弹需要具有一定弹道控制能力。在当今武器系统的研制和实验过程中，利用先进的仿真技术进行建模仿真是一项十分重要的工作。当制导炮弹给定目标运动规律、飞行速度变化和导引方法的条件下，通过运动的建模和仿真能够得出制导炮弹在飞行过程中的任何变化情况，分析主要弹道参数的变化对弹道的影响，对制导炮弹的设计和实验具有重要的意义和价值［11～13］。

本文详细的建立了适用于小型制导炮弹六自由度运动仿真系统的数学模型，引入了模块化设计的思想。在经典力学的基础上进行了运动仿真研究，采用运动学和动力学分析法简化研究的内容，首先把炮弹目标的运动看为质点运动，其次制导与控制系统的工作视为理想状态，最后将参数固化，即不考虑飞行途中的弹体质量、重力加速度、大气密度等等。通过对运动模型的仿真，不仅验证了数学建模的正确性，而且可以表明该模型能够正确地反映制导炮弹的弹道特性。

2 制导炮弹六自由度运动模型

制导炮弹在三维空间中的运动一般可以看为具有六个自由度的运动，依据参数固化原理我们将可变的质量看为常质量系来计算，并且建立了炮弹的运动方程组。在对炮弹的制导和控制系统设计之前，必须知道炮弹在飞行中受到的力和力矩以及其质心的运动规律。制导炮弹运动方程组是描述作用在炮弹上的力、力矩与炮弹运动参数之间关系的一组方程。它由描述炮弹质心运动和弹体姿态变换的动力学方程、运动学方程、炮弹质心变化方程、角度几何关系方程和描述控制系统工作的方程所组成［14］。为了使研究简化，本文主要深入研究了炮弹运动学模型和动力学模型。

2.1 制导炮弹运动学模型

制导炮弹运动学方程组主要描述各运动参数之间关系的运动学方程，其包括弹体质心运动的运动学方程和绕质心转动的运动学方程，其目的是确定质心每一个瞬时的坐标位置以及炮弹相对地面坐标系的瞬时姿态。

2.1.1 制导炮弹质心运动的运动学仿真模型

其中v为导弹速度，θ为导弹弹道倾角，ψc为导弹弹道偏角。

2.1.2 制导炮弹绕质心转动的运动学仿真模型

其中ωxωyωz为弹道坐标系下，炮弹三个不同方向的过载。

2.2 制导炮弹动力学模型

制导炮弹的空间运动可看成变质量物体的六自由度运动，由两个矢量方程描述。为方便研究起见，通常将矢量方程投影到坐标系上，写成三个描述炮弹质心运动的动力学标量方程和三个描述炮弹质心绕质心转动的动力学标量方程。

2.2.1 制导炮弹质心运动的动力学仿真模型

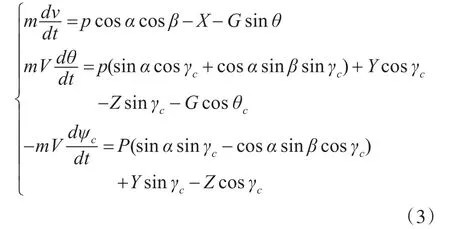
2.2.2 制导炮弹绕质心转动的动力学仿真模型

其中JxJyJz为炮弹对于弹体坐标系各轴的转动惯量；ωxωyωz为弹体坐标系相对于地面坐标系的转动速度在弹体坐标系各轴上的分量；MxMyMz为作用在炮弹上外力矩在弹体坐标系各轴上的分量。

3 运动模型仿真系统设计

3.1 设计思想

利用Matlab/Simulink软件平台，将整个六自由度运动模型仿真系统进行模块化。Simulink具有相对独立的功能和使用方法，仿真模型由方框图表示，实现了可视化建模。Simulink不仅支持线性和非线性系统而且还支持连续、离散以及混合系统［15］。整个运动模型仿真设计分为三步：1）根据运动模型系统的结构及功能，将系统分为若干个子模块，确定各模块的输入输出信号流；2）分别构建各子模块的内容；3）对模块进行封装，形成闭合回路。

3.2 制导炮弹运动学模块

采用定质量六自由度的刚体运动模型，该模型中可计算出炮弹质心在地面坐标系中的位置和弹体的俯仰、偏航、滚转的姿态。根据炮弹质心运动学方程组，可以得出炮弹质心在空间的位置，仿真图如图1所示。根据炮弹绕质心转动运动学方程组，可得出炮弹弹体的俯仰、偏航、滚转的姿态。仿真图如图2所示。

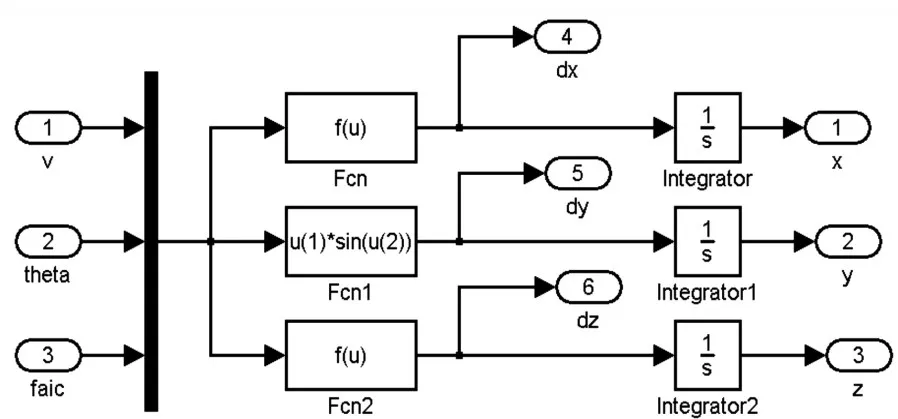
图1 制导炮弹质心运动的运动学仿真模块

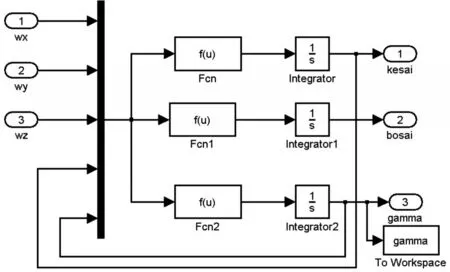
图2 制导炮弹绕质心转动的运动学仿真模块

3.3 制导炮弹动力学模块

该模型计算炮弹在飞行中的气动力与气动力矩，根据飞行力学的知识，计算升力、阻力、等气动力，俯仰力矩、偏航力矩、滚转力矩等气动力矩。根据炮弹质心动力学方程，可以得出炮弹的切向加速度、法向加速度及质心加速度的水平分量，从而更新下一时刻的加速度，如此循环获得导弹的位置速度的连续输出，仿真图如图3所示。根据炮弹绕质心转动的动力学方程组可知，由初始的dωxdωydωz，经过积分器便可以获得了角速度ωxωyωz。因此计算出的角速度作为下一次的输入，这样就可以获得炮弹飞行时连续的角速度状态量。仿真图如图4所示。

4 系统仿真运行结果

4.1 仿真数据初始化

采用运行M文件函数方式对制导炮弹的初始参数进行读写操作。在M文件中设置炮弹的初始基本参数，包括制导炮弹的总体参数、气动参数、控制参数、导引比、初始速度等等。通过运行M文件将初始化数据读入Matlab工作空间，当需要更改参数时，可直接在M文件中进行更改。主要给定的参数如下：

制导炮弹参数：初始速度：V=312m/s；初始位置：x0=0 y0=0 z0=0；初始弹道倾角：θ0=450；初始弹道偏角：ψc=0目标参数：目标速度：V=0m/s；目标初始位置：x0=10km y0=0 z0=0；导引比：k=4；时间常数：Tg=0.3s；风速：V=10m/s以上的参数均封装在6DOF仿真模型中。

图3 制导炮弹质心运动的动力学仿真模块

图4 制导炮弹绕质心转动的动力学仿真模块

4.2 仿真结果

在给定初始条件下进行制导炮弹系统仿真，仿真部分结果如图5～图10所示，依次为制导炮弹弹道曲线，制导炮弹速度曲线，制导炮弹过载图，攻角、侧滑角，偏航角、俯仰角、滚转角和弹道倾角、偏角。

通过图5和图6可知，制导炮弹经过无控段、弹道转弯滑翔段、末端制导攻击段三个阶段，最大飞行高度为1800m左右。制导炮弹速度从开始的312m/s开始衰减，最终保持200m/s左右。通过以上得到的仿真曲线，可以得知构建的炮弹运动仿真模型是正确的。

通过图7和图8可知，当制导炮弹发射时初速度较快，此时弹体受到风速的影响而发生小范围上下和左右的摇摆，从而使切向过载和法向过载上下变化，攻角和侧滑角也在发生变化。当炮弹发射40s后，从过载图和攻角、侧滑角图可以看出曲线基本保持不变，从而得出弹体基本处于平稳滑翔阶段。

图5 制导炮弹弹道曲线

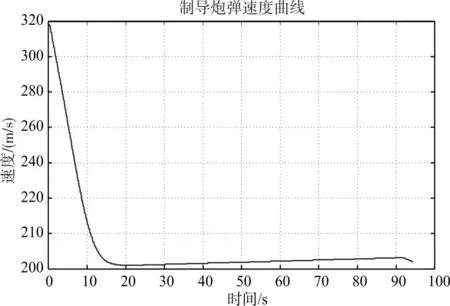
图6 制导炮弹速度曲线

图7 制导炮弹过载

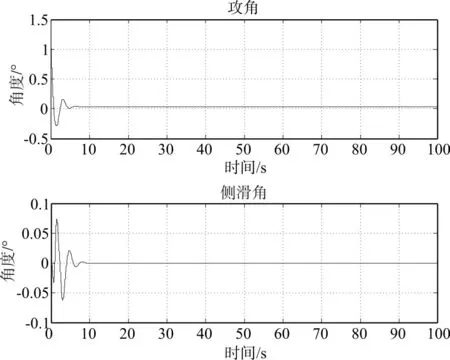
图8 攻角、侧滑角

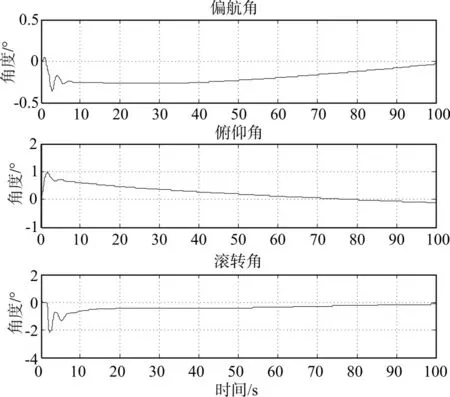
图9 偏航角、俯仰角、滚转角

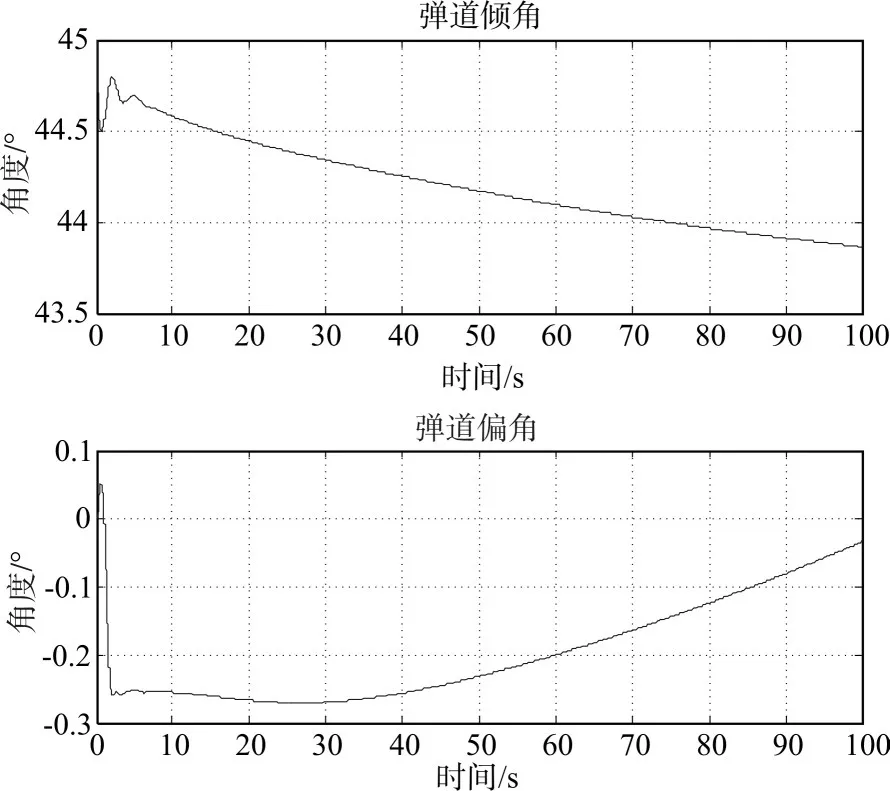
图10 弹道倾角、偏角

通过图9和图10可知，炮弹以倾角45°发射后，弹体进入偏航、俯仰和滚转通道的调节，经过几个周期的调整，基本处于可控的扰动范围，从而对目标进行精确打击。

5 结语

在分析制导炮弹运动的基础上，采用了Matlab工具对制导炮弹进行运动模型仿真，文中构建的运动模块仿真系统具有较强的通用性和可扩展性，每个子系统又可以独立进行仿真研究，同时可以在系统任何阶段修改模型参数。仿真结果表明：建立的制导炮弹运动模型能较好的反应系统的实际情况，仿真结果接近实际系统。可以根据仿真模型来分析制导炮弹的弹道，对制导炮弹控制系统的设计研究和性能测试具有一定的参考价值，但是在建模过程中为了便于分析问题，简化了许多因素，因此还需进一步精确仿真分析。