基于降采样和fdesign+design的IIR滤波器的设计∗

吴 冉阮 晨

（1.南阳理工学院计算机与信息工程学院 南阳 473004）（2.华中科技大学 武汉 430074）

1 引言

在信号处理过程中，有用的信号往往混有噪声，根据有用信号和噪声的特性差异，提取有用信号的过程称为滤波［1～2］，实现滤波功能的系统叫滤波器，滤波器又有模拟和数字之分。由于数字化的普及，数字滤波器已经得到了广泛的应用［2～5］，家用电视机，电脑；医用各种扫描设备、核磁共振仪；军用雷达监控设备，飞机，导航系统等都用到了数字滤波器。根据冲激响应的不同将数字滤波器分为有限冲激响应FIR（Finite Impulse Response）数字滤波器和无限冲激响应IIR（Infinite Impulse Re⁃sponse）数字滤波器［6～7］。IIR数字滤波器又包括巴特沃斯数字滤波器，切比雪夫I型数字滤波器，切比雪夫II型数字滤波器，椭圆型数字滤波器［8］。有两种方式可以实现数字滤波器，第一，用计算机软件编程实现，第二，设计专用的数字处理硬件。计算机软件编程就是要用Matlab提供的信号处理工具箱来实现数字滤波器［4，8］。Matlab工具箱提供了大量的函数，只要指标参数设计正确，然后调用函数就可以方便快速地设计数字滤波器。Matlab使复杂的程序设计简化成函数的调用。有时调用了Matlab函数设计数字滤波器，得到了数字滤波器系数，然后对测量数据进行数字滤波，却发现滤波器的输出数据会溢出或者完全没有数据输出，画出的图是空的。这种现象出现的原因是滤波器设计时参数给得不合理，例如过渡带太窄［9～10］，求得的滤波器阶数太高，滤波器不稳定，造成数据出现inf或NAN。文中结合实例通过“降采样”的方法，以及“fdesign+design”方法编程实现的IIR数字滤波器-巴特沃斯数字滤波器可以有效地解决上面的问题。

2 结合实例进行分析

信号从fjndata.mat文件读入，它由数个正弦信号与随机噪声叠加而成，采样频率为250Hz。信号中有一个5Hz的正弦信号，要求设计一个巴特沃斯滤波器，通带频率为1.5Hz～10Hz，阻带频率为1Hz和12Hz，通带波纹Ap=3，阻带衰减As=15。IIR数字滤波器-巴特沃斯滤波器部分程序清单如下：

仿真以后得到巴特沃斯数字滤波器的幅频曲线如图1所示。

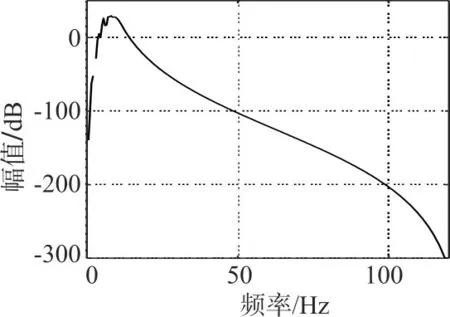
图1 巴特沃斯数字滤波器的幅频曲线

计算出的巴特沃斯数字滤波器的阶数是16阶（等效的低通滤波器是8阶，转到带通为16阶），但从图1可以看出，在频率3Hz附近，幅频曲线不连续，如果在Matlab的工作区查看幅值H的值，可以看到H的第6个值是Inf（无穷大），这样的滤波器显然不适合做进一步的滤波处理（如果滤波一定会发生数据溢出，甚至也会产生Inf或NAN）。上述实例中，采样频率为250Hz，通带频率为1.5Hz～10Hz，该通带的中心频率：

采样频率 fs与带通滤波器的中心频率 f0之比有将近65倍之高，这就是造成滤波器失调的原因，过渡带太窄，导致求得的滤波器的阶数太高。由于滤波器系统不稳定造成数据出现inf或NAN的原因将在后面分析。

3 降采样方法设计巴特沃斯数字滤波器

通过降低信号的采样频率，再以降低的采样频率设计数字滤波器，降采样后，新的采样频率为fs1，一般应使 fs1/f0＜15较合适，本次仿真把采样频率降为1/5，为50Hz，部分程序清单如下：

程序运行中首先将信号降采样到50Hz，巴特沃斯数字滤波器是在采样频率为50Hz的基础上设计的，得到的巴特沃斯数字滤波器的幅频响应曲线如图2所示。

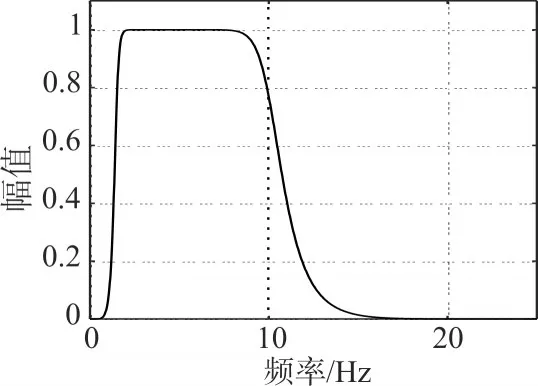
图2 降采样设计的巴特沃斯数字滤波器的幅频曲线

从图2可以看出“降采样”以后，巴特沃斯滤波器的幅频曲线不连续情况得到了改善，响应曲线很好。

滤波前的信号波形、降采样后的信号波形与滤波后恢复原始采样频率后的输出波形如图3所示。

从图3可以看出“降采样”以后，巴特沃斯数字滤波器的滤波效果很好，所设计的巴特沃斯数字滤波器是合格的。

4 fdesign+design方法设计巴特沃斯滤波器

文中第2部分设计的IIR数字滤波器-巴特沃斯数字滤波器产生了溢出，经降采样频率后才解决，现在用fdesign+design方法在相同的参数条件下设计相同的数字滤波器。程序清单如下：

程序先用fdesign函数给出滤波器的参数集合，运行调用designmethods（d）函数以后，从命令行窗口可以看到本程序的指标适合设计巴特沃斯、切比雪夫I型、切比雪夫II型和椭圆型数字滤波器，如图4所示。

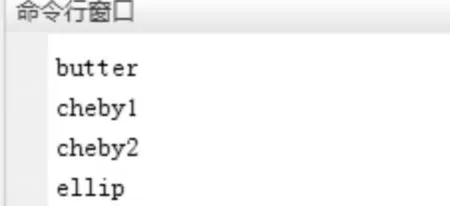
图4 适合的数字滤波器

实例中设计的是巴特沃斯数字滤波器，所以为了保证相同条件，调用design函数，设计巴特沃斯数字滤波器，得到系数集合 hd，最后通过 fvtool［11～13］画出巴特沃斯数字滤波器的幅值响应曲线，如图5所示。

从图5可以看出巴特沃斯数字滤波器的幅值响应曲线与图2降采样以后的幅值响应曲线几乎相同。用fdesign+design设计的巴特沃斯数字滤波器虽然也一样得到16阶的滤波器，但由于它把滤波器分解为8个二阶滤波器的级联，使它的幅值响应不通过降采样一样可以得到满意的结果。所以fdesign+design法也能用来设计“窄带”的滤波器。

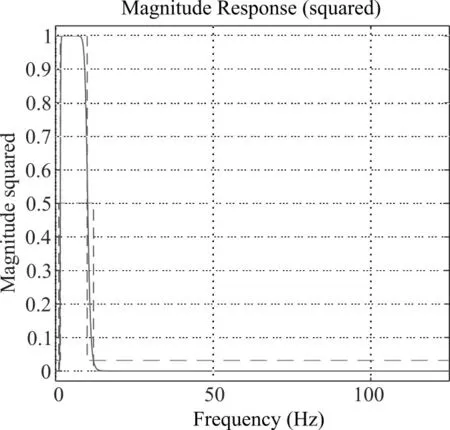
图5 fdesign+design设计的巴特沃斯滤波器幅频曲线

下面分析滤波器系统为什么会出现不稳定性。用fdesign+design函数编程的第二部分，把巴特沃斯滤波器系数集合Hd通过tf函数，得到IIR型滤波器系统函数的分母A和分子B（这和实例中滤波器A、B的值一样），A的极点反映了该系统的稳定性，用fdesign+design函数编程的第二部分计算了A的极点如下所示，第一列表示编号，第二列表示实部，第三列表示虚部，第4列表示模值。

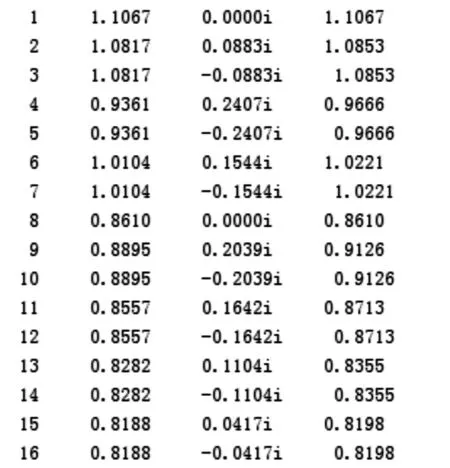
一个稳定的系统是要求所有的极点都在单位圆内。但从以上结果可以看出，极点编号1～3和6～7这5个极点都在单位圆外（模值大于1），这说明了该滤波器的不稳定性。因此在滤波过程中会出现NAN或Inf的数值。

5 fdesign+design方法设计IIR数字滤波器的优点

设计一个低通滤波器，通带频率为0.25，阻带频率为0.4，通带波纹为Ap=0.25dB，阻带衰减为As=40dB，要求同时设计4种IIR滤波器。程序清单如下：

运行调用designmethods（d）函数以后，从命令行窗口可以看到本程序的指标适合设计巴特沃斯、切比雪夫I型、切比雪夫II型和椭圆型数字滤波器，所以在调用design函数时用了‘alliir’参数，即同时设计允许的4种滤波器。通过fvtool画图得到4种数字滤波器的幅值响应曲线，如图6所示。

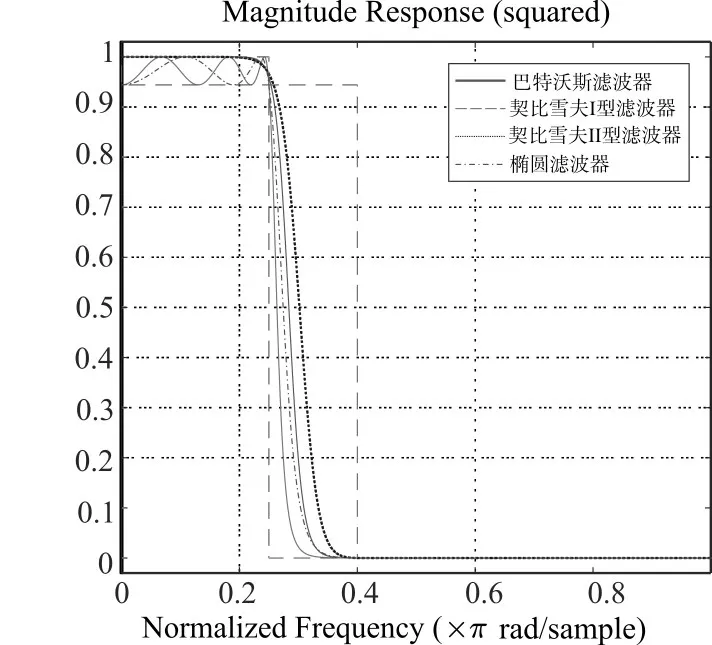
图6 4种数字滤波器的幅值响应

从图6中可以看出，用fdesign+design方法可以一次设计4个IIR滤波器，但经典方法［11］要用多个语句才能设计4个IIR滤波器，这里用一个语句就可以。

6 结语

文中结合实例分析了滤波器的输出数据溢出的原因，一是过渡带太窄，滤波器阶数太高，二是滤波器系统不稳定，并对滤波器系统不稳定的原因进行了解释，用“降采样”和“fdesign+design”的Matlab编程方法设计的巴特沃斯数字滤波器，有效地解决了滤波器的输出数据溢出的缺点。仿真表明“fde⁃sign+design”的方法不用通过“降采样”也可以得到满意的结果，而且用fdesign+design方法可以一次设计4个IIR滤波器，比经典方法要简单。广大设计人员可以根据自身情况选择快捷的方法实现I巴特沃斯数字滤波器的设计。