基于能力谱法的桥墩横向抗震性能评价

臧 博

（山西省交通科学研究院，山西 太原 030006）

0 引言

传统的抗震设计采用基于结构承载能力的方法，例如89抗震规范[1]，其设计理念为“一水平设防，一阶段设计”，即只进行弹性抗震设计。为了应对较强的地震，采取加大构件截面和增加配筋的手段以提高其抗力。截面越大，刚度就越强，对于大部分结构来说，其后果就是地震力进一步增大，如此就陷入了恶性循环。

近年来，有学者提出基于性能的抗震设计思想[2]。公路桥梁抗震设计细则[3]的“两水平设防，两阶段设计”理念，也体现了这种思想。在第二阶段抗震设计（延性抗震设计）中引入了“能力保护设计”概念，并且在求取排架墩横向位移时推荐使用非线性静力分析法（Pushover）。

Pushover结合能力谱法可以简单方便地评估结构抗震性能。能力谱最初是由Freeman等人提出，经过不断改进，现已作为美国应用技术委员会推荐的抗震性能评估方法[4]。该方法在建筑结构中已经得到广泛应用，而在桥梁结构中应用还比较少。本文采用Pushover和能力谱法，结合工程实例进行横向抗震性能研究。

1 Pushover基本原理

Pushover是一种静力弹塑性分析方法，其基本思路是逐步增大对结构施加的侧向荷载，使结构直至倒塌或者达到目标变形状态，用以研究结构在非线性状态下的性能，考察其变形能力能否满足要求。

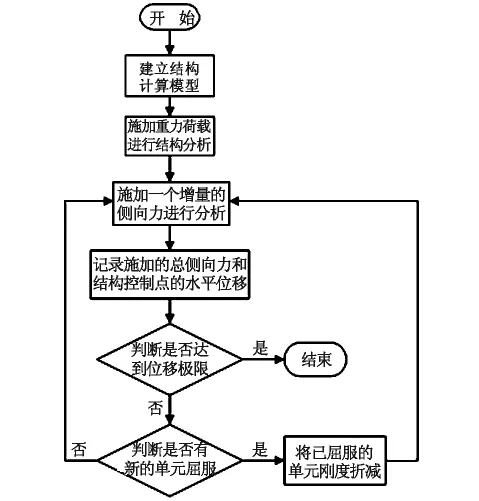
图1 Pushover分析流程图

1.1 基本假定

对于以第一振型为主的常规结构，可用等效单自由度体系对结构进行模拟，同时假定结构的形状向量{Φ}保持不变。

1.2 侧向荷载分布模式

采用Pushover方法评价桥梁结构的抗震能力时，应对结构采取合理的侧向荷载分布模式。为精确地得到结构地震响应，通常采用与结构的第一振型相似的分布模式，主要有如图2中几种形式。

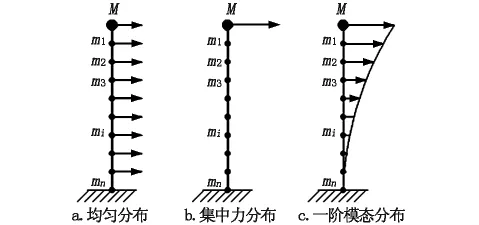
图2 Pushover加载模式

在实际运用过程中，可以采取均匀分布模式来估计结构地震反应的上限，采取集中力分布模式来估计结构反应的下限[5]。

2 能力谱法

单纯地推倒分析并不能得到地震响应值，还需要结合能力谱法以确定结构在指定地震强度下的反应值。本文使用能力谱法，即将地震需求曲线和结构能力曲线绘制在同一坐标系，以评估结构的地震响应。

由于能力曲线一般采用荷载-位移格式，而需求曲线（阻尼比5%的弹性反应谱）一般采用拟加速度-周期格式，二者无法直接比较。需要通过一定的方式转换为统一的AD格式，即能力谱和需求谱，二者的交点即为性能点。

2.1 能力谱的转换

由Pushover得到结构的底部剪力-顶部位移曲线（Vb，u），按照式（1）、式（2）转换为能力谱（Sd、Sa）：

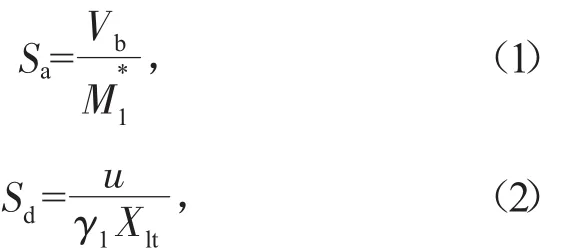
2.2 需求谱的建立

规范一般给出的是阻尼比5%的弹性反应谱（T，Sa），按照式（3）转换为需求谱（Sd、Sa）：

本文采用延性比法折减弹性需求谱以得到弹塑性需求谱，具体参数参照文献[6]推荐的Vindic关系模型：

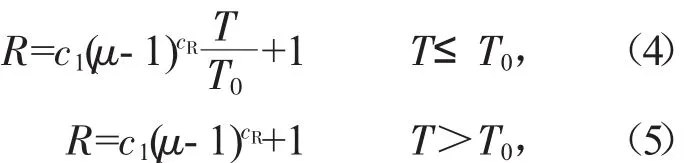
式中：Tg是特征周期；c1、c2、cR、cT等参数取决于结构的滞回性能和阻尼比，参数取值见表1。

表1 Vindic模型参数

按照上述方法，结合本桥的地震动参数（Tg=0.45 s，Ⅱ类场地），将公路桥梁抗震细则规定的E2地震设计反应谱转换为需求谱，如图3所示。

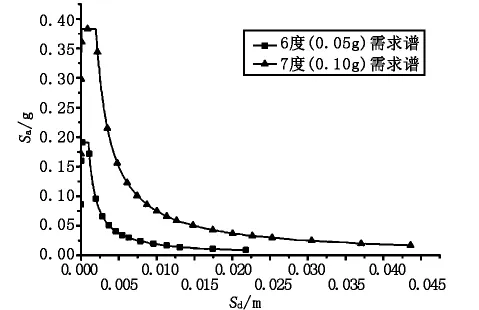
图3 桥位处不同烈度的需求谱曲线

2.3 求取性能点

ATC-40中给出了计算目标位移的迭代计算方法，具体如下：

a）假设谱位移 Di=(Te，ζ)，其中 Te是结构的基本周期，ζ是阻尼比，取0.05。

b）根据能力谱屈服位移Dy，计算延性系数μ=Di/Dy。由μ计算得到等效阻尼比ζeq。

c）根据等效阻尼比ζeq，将弹性反应谱折算作为需求谱。并将Pushover分析所得能力谱与需求谱相叠加，交点处对应的位移即为谱位移Dj。

d）若Di、Dj误差不超过5%，则目标位移等于Di。否则令 Di=Dj，重复 b）～d）。

3 算例分析

3.1 计算分析模型

晋蒙黄河大桥引桥采用三柱式桥墩，本文选用其中一个具有代表性的桥墩：盖梁高2.2 m，墩净高21 m，柱径1.6 m，桩径1.8 m，墩柱采用C35混凝土，桩基采用C30混凝土，纵筋采用32Φ28 mm，箍筋选用φ10@100/150 mm。采用Midas软件进行计算Pushover分析，盖梁、系梁、墩柱、桩基均用梁单元模拟，桩侧土体等效为土弹簧，弹簧的刚度通过“m法”计算，墩柱上下端设置塑性铰。计算模型如图4所示。

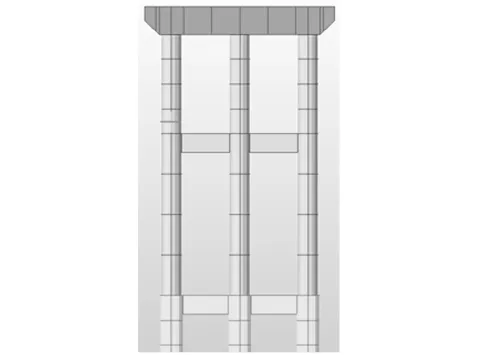
图4 计算分析模型

3.2 Pushover分析能力曲线

本文在1.2节所述的侧向力加载模式中，选择集中力分布、均匀分布、一阶模态分布3种模式，对结构进行Pushover分析，以使分析结果尽可能地接近真实地震响应。将得到的底部剪力-顶部位移曲线，结合动力特性分析得到的基本振型、参与质量、参与系数，按2.1节所述的方法转换为能力谱。如图5所示。

图5 桥墩不同加载模式下的能力谱曲线

由图5可以看出，在本文所采用的3种加载模式下，结构的能力谱曲线变化趋势较为一致。其中，集中力分布和一阶模态分布的谱加速度较为接近（也即屈服剪力较为接近），均匀分布和集中力分布的谱位移较为接近（也即屈服位移较为接近）。

3.3 性能评价

按照2.3节的迭代方法求得的能力谱与需求谱的交点，就是结构在于地震作用下的性能点，意味着结构的最大非线性承载力和最大位移。该点在目标性能控制范围内，则表示该结构能够满足性能要求。将不同加载模式下能力谱与需求谱的交点列于表2，并给出对应的墩底剪力和墩顶位移。

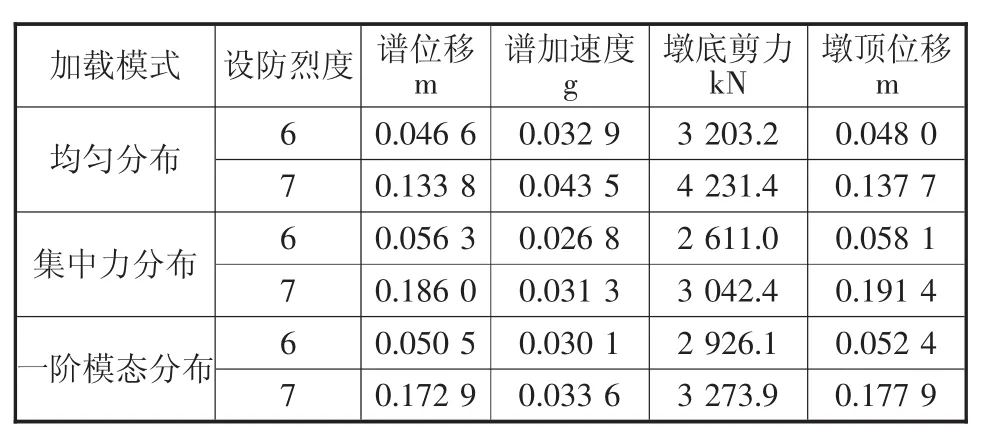
表2 桥墩横向响应值（规范反应谱）

需求谱曲线与各加载模式下的能力谱曲线均存在交点，表明结构可以抵抗6度、7度设防地震强度，且结构在6度设防地震烈度下处于弹性状态。从表2中的剪力、位移来看，在6度设防地震烈度下，各加载模式下的墩底剪力和墩顶位移相差不多；而7度设防地震烈度下，集中力分布和一阶模态分布下的墩底剪力和墩顶位移较为接近。

4 结论与展望

本文介绍了Pushover分析的基本原理和应用方法，采用能力谱法评价了实际工程中桥墩结构的抗震性能。分析结果表明：

a）均匀分布、集中力分布两种侧向力加载方式可以估计结构能力谱的上、下限。

b）算例结构可以抵抗6度、7度设防地震强度，且在6度设防地震烈度下结构处于弹性范围内。

由于篇幅所限，文中仅对结构一个方向的抗震性能进行了简单评价，而实际地震运动则是多维的、往复的，如何将Pushover分析方法推广到多维地震下结构抗震性能评价中，将是一个值得研究的课题。