基于粒子群算法的配网风机接入研究
徐舟鹰 乐恩典
(国网舟山供电公司,浙江舟山316021)
0 引言
随着通信技术的不断进步,大数据的发展势不可当,“数据即资产”的观念已被大多数人所认同。与此同时,在全球能源互联网大力发展的背景下,国内外的电力发展正经历着很大的变化,大量分布式可再生能源开始接入配电网,如风电、光伏等,它们的接入会对配电网的可靠性产生重大影响,且会增加配电网的运行数据。如何利用配网中海量的运行数据对其建立量化的可靠性评估方法成为了研究热点。
本文介绍了改进粒子群算法(Improved Particle Swarm Optimizer,IPSO)的特点和原理,并将其运用到具有分布式电源的配电网运行中去,在解决问题时采用权重系数进行多目标优化,最终通过对算法的改进提高了寻优效率。
1 粒子群算法简介
粒子群算法(Particle Swarm Optimization,PSO)是根据鸟类觅食的过程进行的一个生物优化算法,是基于一个群体的智能算法对一个复杂问题进行分析和优化的过程,对于多目标问题反应灵敏、计算快,但同时容易陷入局部最优。
2 粒子群算法在中压配电网中的应用
粒子群算法在中压配电网中主要用于开关站的选址,开关站的模型通常包含经济模型和可靠性模型,本文在考虑这两者的基础上,使用一个综合模型作为粒子群算法的迭代标准。在现阶段的配电网运行中,如何采用海量运行数据对各种分布式新能源的接入和运行进行选址也至关重要。
2.1 风电开关站经济模型
风电所需要建立的开关站的经济模型主要包含其投资和运行费用,采用等年值法:

式中,M为风机开关类型总数;Nj为第j种类型开关新增数目;Csj为第j种开关目前单价;Pj为第j种开关使用寿命;Cs为总开关投资的等年值。
风机的运行费用(年度费用)由式(2)得出,其大小和开关站的总投资成正比。

式中,CM为风机运维费用;H为比例系数。
2.2 风机可靠性模型
在配电网中,开关站的可靠性主要与其是否停电有关,无论是计划停电还是故障停电。由停电造成的损失计算如式(3)所示:
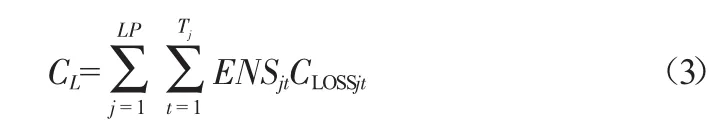
式中,LP为负荷节点数;Tj为第j个负荷点的停电类型;ENSjt为负荷点j第t停电相应所失去的供电量;CLOSSjt为负荷点j第t停电的单位停电损失;CL为年度停电损失总费用。
2.3 风机运行综合模型
配电网风机接入的综合模型考虑使用权重因子将两种模型整合,通过不同种类的运行方式,考虑经济性和可靠性的占比,得到综合模型如式(4)所示:
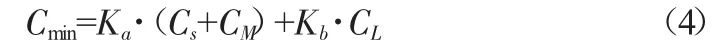
式中,Ka、Kb为经济性、可靠性权重因子,Ka+Kb=1。
2.4 计算步骤及流程
分布式电源接入配电网通常分为多电源接入和单电源接入。
2.4.1 单独风机接入过程
在配电网只有一个风机时,风电的供电范围是确定的,只需要根据政府规划和供电需求确定其装接位置即可。将该区域的粒子位置代入上述式子中,可以得到每个粒子的“适应度”,通过对“适应度”的对比和判断,评价该粒子所处的环境,以及如此建设和运行是否经济。通常来说,“适应度”越低对应着其所需要的投资成本以及后期运营成本越低,而对于所有的“粒子”的位置所对应的总“适应度”的最低点即最优的投放位置。
具体步骤如下:
(1)随机给定n个粒子的位置,即代表风机的装接位置;
(2)计算各个粒子位置所对应的“适应度”,即该位置装接风机的成本;
(3)根据上述粒子产生的最优解进行位置调整,采用实际情况对“适应度”函数进行优化,完成一次搜索,每一次迭代都再进行上述步骤,直到寻找到最优点;
(4)最后停止循环得到最优位置。
2.4.2 多风电机组接入电网过程
多个风机接入电网的步骤同一台风机接入类似,只是最后的结果需要输出一组变量组成的最优解的合集作为每个风机的布点。除了考虑风电的容量外,也要考虑其在该供电位置的供电范围。根据粒子群算法的步骤,就需要对m个目标进行优化,同时得到其“适应度”的和的最小值,才是这m个风机所要的最优位置。
具体步骤如下:
(1)确定每个风机的供电范围,通过随机数的放置测得每个负荷点到该电源点的距离作为参考,并判断该容量是否符合要求;
(2)容量满足要求的风机就不再进行划分,其余风机直到划分完毕即可,接着在每个点的范围内确定风机最优位置,即重复单风机的优化步骤即可,直到获得最优解。
3 算例分析
根据需要,建一个规模为2×50 MW的风电站和一个规模为1×50 MW的风电站,线路的贴现率为0.08,折旧年限为16,新建站出线单位长度投资费用均为150万元/km,网损折算系数α1=α2=α3=0.004 69(假设线路全年投入运行),具体信息如表1所示。
从图1中可以看出,运用粒子群算法求解电力系统开关优化问题具有良好的性能,经过多次运行程序,均能在20代以内收敛到最优解。
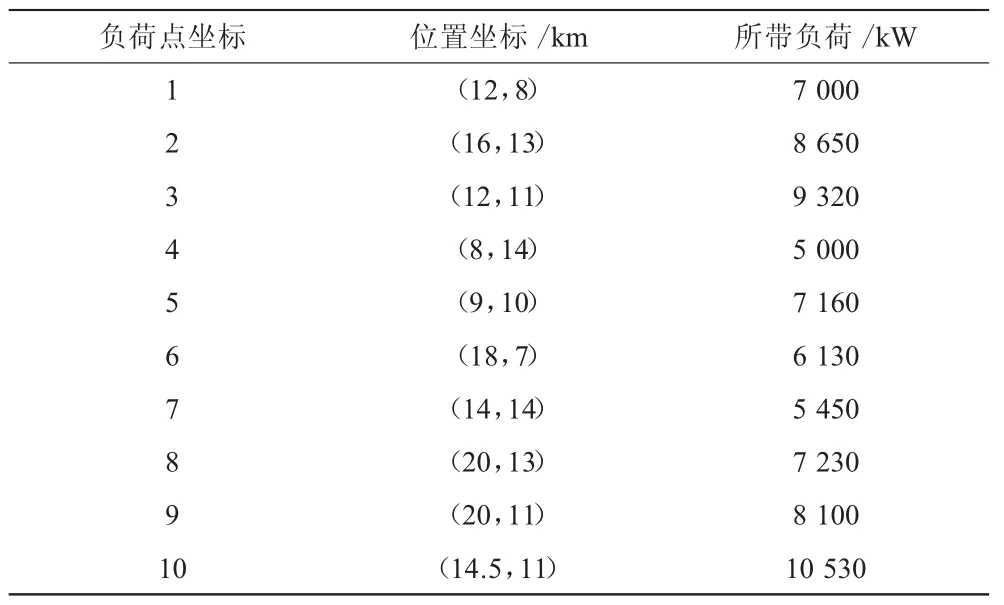
表1 负荷坐标信息表
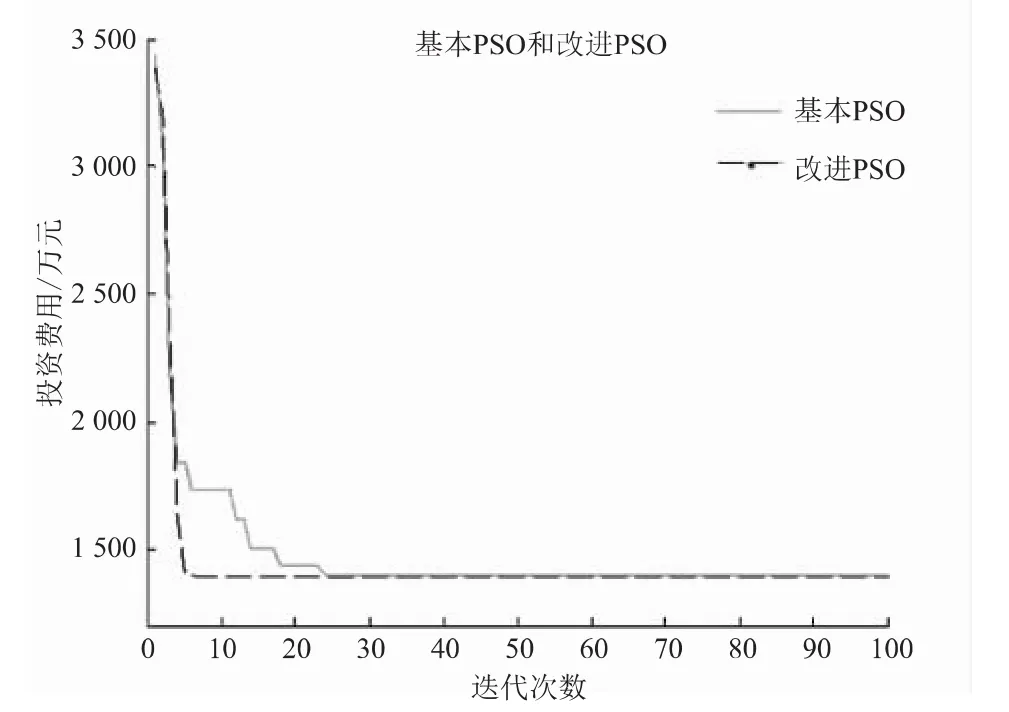
图1 粒子群算法趋势图
4 结论
随着分布式能源接入配电网,采用最优方法配置负荷成为配电网中一个十分重要的问题,其社会价值、工程经济价值都有显著提高。本文在研究风机的配置后得出了以下结论:
(1)通过对风机电源点的划分,可以简化计算过程,节省搜索时间,减少计算量,从而快速高效地得到系统的经济性指标;
(2)根据配电网中风机开关站优化的特点,将改进粒子群算法运用到计算中,相对于原始方法效果更佳,算法精确有效。

