一种基于分子结构设计理论的聚类分析方法

张西宁, 雷 威, 唐春华, 向 宙

(西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，西安 710049)

故障诊断的本质属于模式识别，即当输入矢量属于不同类别时，对该矢量所属类别做出正确的判断，亦称聚类[1]。故障诊断包括信号采集、特征提取和状态识别三个环节，其中信号采集是故障诊断的前提，特征提取是关键，而状态识别则是故障诊断的核心[2]。

故障诊断的经验方法通常需要具有已知故障类别的信号样本进行监督训练，然而，在实际故障诊断中很难得到不仅完备而且具有良好通用性的故障样本[3]。无监督聚类在没有任何已知样本学习的前提下，通过分析数据的内在结构，根据样本相似度或概率密度函数估计方法实现样本的正确分类[4]。无监督聚类因其实现不需要任何训练样本，广泛应用于入侵检测[5-7]、图像处理[8-9]、数据挖掘[10]、故障诊断[11-14]等领域。

无监督聚类方法可以被分为以下几类：基于划分的方法、基于层次的方法、基于网格的方法、基于密度的方法以及基于模型的方法[15]。常用的基于划分的聚类方法有K-均值、K-中心点以及CLARA法(Clustering Large Applications)等；基于层次聚类方法的有BIRCH法(Balanced Iterative Reducing and Clustering using Hierarchies)、CURE(Clustering Using Representatives)法等；基于网格的方法有STING(Statistical Information Grid)、WaveCluster等；基于密度的方法有DBSCAN(Density-Based Spatial Clustering of Applications with Noise)、OPTIC(Ordering Point to Identify the Cluster Structure)等；基于模型的方法有竞争学习、SOM(Self-Organizing Map)等[16]。此外，主分量分析(Principal Component Analysis,PCA)也是一种能够发现数据模式和结构的无监督聚类方法[17]。

无监督聚类算法多种多样，每种方法都有其优缺点。比如，基于模型的聚类方法SOM具有可视化、拓扑结构保持以及概率保持等优点[18]，被广泛地应用于语音识别、模式聚类、组合优化等众多信号处理领域。但也存在着许多不足[19]：当样本数据维数较高时，其从高维到低维的映射会出现较大的畸变；而且聚类结果容易受连接权向量的初始状态的影响；“死神经元”现象导致学习效率低，收敛时间长。杨松等[20]针对 SOM 网络在分类中由于其初始权值的随机性而导致的训练次数过多且易陷入局部最小的问题，提出了利用遗传算法改进网络初始权值的设置。邹瑜等[21]针对SOM在图像分割中，随着神经元数量增加，网络分割性能变差，且无法分割噪声强度过大的图像的问题，提出将有限脉冲响应(FIR)加入SOM，把每个神经元作为FIR系统，分割效果优于基于SOM的方法。陶刚等[22]提出了一种改进的SOM聚类离散化算法，利用SOM实现初始聚类，以初始聚类中心为样本，通过层次方法BIRCH进行二次聚类，有效地解决了大样本，高维数据离散化问题。此外，大部分无监督聚类方法在聚类过程中仅考虑类内元素的关系而忽略了类间元素的关系，从而丢失掉了类间元素的相对位置以及距离信息[23]。

针对上述无监督聚类算法中存在的问题，本文提出了一种基于分子结构设计理论的聚类分析方法。该方法将故障样本空间看作分子系统，将故障样本看作分子系统中的原子，以故障样本之间的差异度作为分子势能的度量指标，在故障样本间“相互作用势”的影响下，以样本间“势能”最小为依据，调整故障样本在映射平面上的位置，从而获得最佳的聚类效果。本文以滚动轴承和柴油机的故障数据为例进行聚类分析，并与SOM聚类方法进行对比，验证所提方法的有效性。

1 分子结构设计理论

分子力学是模拟分子行为的一种计算方法，分子力学认为分子体系的势能函数是分子体系中原子位置的函数[24]。这些原子在空间上过于靠近，便互相排斥；但又不能远离，否则连接他们的化学键以及由这些键构成的键角等会发生变化，引起分子内部应力的增加。分子力学从本质上说是能量最小值方法，即在粒子间相互作用势的作用下，通过改变粒子分布的几何位型，以能量最小为依据，从而获得体系的最佳结构[25]。

分子结构设计的流程如图1所示，首先给出分子中各原子的初始坐标及其连接关系；其次按不同的联接关系，选择不同的势能函数以及势能场参数；计算分子空间内的总势能，即原子间势能的叠加；然后求出分子空间内势能场的最小值点；更新原子在分子空间的坐标，并进行循环迭代直到原子位置收敛。

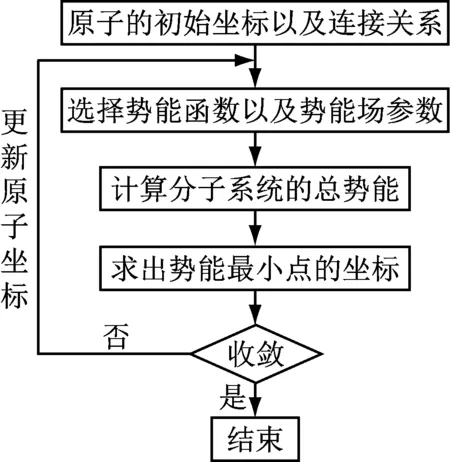
图1 分子结构设计的流程

2 基于分子结构设计理论的聚类分析方法的原理

借鉴分子结构设计的思想，提出一种新的聚类分析方法。该方法由两层网络结构组成:第一层为输入层，节点数目与数据样本维数相同；第二层为决策层(决策平面)，其形式可以是二维棋盘平面，也可以是三维空间结构。本文以二维棋盘平面为例进行说明，其结构示意图如图2所示。

图2 基于分子结构设计理论的聚类方法的结构图

Fig.2 The structure of clustering method based on the theory of molecular structure design

以滚动轴承的故障模式聚类为例，假设共有N组，每组数据M维特征的故障特征集X={xn,n=1,2,3,…,N}。

(1)

(2)

将滚动轴承振动数据样本空间看作分子系统，将每个故障样本看作分子空间中的原子，以故障样本之间的差异度作为原子间相互作用势能的度量。

类似的，设样本之间的势能函数为

E=|s-d|a

(3)

式中：E为样本间的势能；s为故障样本在决策平面上的欧氏距离；d为势能场参数，此处为样本间的差异度；a用于控制样本间势能场随距离增减的幅度。当a=1时，势能函数为线性函数，适用于样本间差异比较明显的情况;当a≥2时，势能函数为非线性函数，适用于样本间差异不是很明显的情况。其示意图如图3所示，示意图中参数a设为2。从图中曲线的趋势可以看出当故障样本在决策平面上的距离较小时，样本间的势能较大。随着故障样本在决策平面上的距离逐渐增大，样本间的势能逐渐减小；当故障样本在决策平面上的距离达到一定程度时，样本间的势能将达到最小；然后随着故障样本在决策平面上距离的增大，样本间的势能同时也增大。参数d作为样本间的差异度指标，从图3中可以看到当d较小时，势能函数的最小值点对应的样本间距离较小；当d较大时，势能函数的最小值点对应的样本间距离较大。势能函数的这些性质保证了相似的样本会被放置在较近的位置，而不相似的样本则会被放置在较远的位置。

图3 样本间相互作用示意图

本文方法的流程与图2所示的分子结构设计流程相似。首先对每个故障样本在决策平面的坐标进行初始化，在给定的势能函数以及势能场参数的情况下，计算某个故障样本与其他所有故障样本相互作用产生的势能场，计算这些势能场的矢量和，求出势能场内的最小值，此点即为在其他故障样本的共同作用下与该故障样本势能最小点的位置，并以此位置更新该故障样本在决策平面的坐标。类似的，计算其他样本的势能最小点的位置，并以此更新该故障样本的坐标。在将所有故障样本的坐标更新完成之后，重新计算上述过程，直到故障样本在决策平面的坐标收敛。

收敛准则可以描述为

(4)

式中:P,P′分别为算法中样本点在上次迭代和本次迭代的坐标；MapX为决策平面的边长；m的值建议选为1/MapX，本文中取m=0.1。

在故障样本的坐标收敛后，相似的样本被放置到比较近的位置，差异较大的故障样本则被放置到较远的位置，完成故障样本的聚类。假设有N组，每组数据M维特征的滚动轴承振动信号故障特征集，本文方法的具体步骤如下：

步骤1将N组故障样本按照式(2)进行标准化，然后按照式(1)计算样本之间的差异度，并初始化N组样本在决策平面上的坐标；

步骤2按照式(3)选择势能函数，设置势能场参数a；

步骤3①第1组故障样本与其他样本相互作用产生的势能场为

E1=E1,2+E1,3+…+E1,n+…+E1,N

(5)

式中：E1,n=|S1,n-D1,n|a，S1,n为样本1和样本n在决策平面上的欧氏距离

(6)

②求出当势能E1取最小值的坐标，并以此坐标更新第1组故障样本在决策平面上的坐标；

③重复①、②更新所有故障样本在决策平面上的坐标；

步骤4对比故障样本更新前后的坐标，如果坐标不再变化，结束算法；否则，重复步骤3直到所有样本点收敛。

如前面分析，在SOM聚类过程中网络连接权值的初始状态对网络的收敛性能有较大的影响。本文方法虽然需要对故障样本的初始位置进行初始化，但是无论故障样本的初始位置如何，由于故障样本之间的差异度确定，在多次迭代后样本的相对位置固定，因此减少了初始状态对聚类结果的影响。并且势能函数保证了相似的样本会被放置在较近的位置，而不相似的样本则会被放置在较远的位置，降低映射过程中的畸变。本文方法不仅考虑类内元素的关系而且考虑了类间元素的关系，因此能够保留原始样本不同模式间的相对位置以及距离信息。

3 滚动轴承振动测试实验

本次实验使用实验台如图4所示。该滚动轴承实验台由直流电机、滚动轴承安装架、加载装置和滚动轴承等部分构成。实验轴承选用了四种状态的6308深沟球轴承，分别是正常、内圈剥落、外圈剥落和滚动体剥落。实验时轴承内圈转速为1 200 r/min，传感器为IMI的601A11加速度传感器，数采卡为UA300系列数据采集卡。采样频率10 kHz，采样时间持续10 s。

图4 滚动轴承实验台

每种状态采集8组数据，共有32组数据。本文提取了滚动轴承振动信号的均方幅值、峰值、平均幅值、峰值指标、峭度指标、K因子、脉冲指标、波形指标等8个时域参数。

首先使用SOM聚类方法对轴承故障数据进行聚类。将特征向量进行归一化作为SOM神经网络的输入，输入层神经元数目为8，输出层神经元数目为100。SOM神经网络使用Mexihat函数调整侧向抑制的邻域，更新权值学习率的函数采用式(7)

(7)

式中：α0为初始的学习率；α为当前步的学习率；t为当前迭代的步数；T为设定的总的迭代步数。

SOM对轴承数据特征的聚类结果如图5所示，图中四种颜色分别表示四种类型的轴承故障。从图中可以看到四种类型的故障基本能够被区分开，但是其中属于同一种故障模式的样本在图中的距离较远，比如点25和点28；而不属于同一种故障模式的样本在图中的距离较近，如点5和点25。第25组样本与第28组样本都属于滚动体剥落，其欧式距离为0.078 4。第5组样本与第25组样本属于不同的故障模式，其欧氏距离为0.344 0。在原样本空间，第5组样本与第25组样本距离较远，第25组样本与第28组样本距离较近。但是在经过SOM映射到二维平面，样本间的位置关系出现了畸变。

本文方法设置决策平面大小为10×10，势能函数选为线性函数E=|s-d|。使用本文方法的聚类结果如图6所示，图中椭圆图形是为了方便观察而加上的。从图中可以看到四种类型的故障样本被很好的区分开，而且同种故障模式的样本在映射到决策平面后，其在平面内的距离较近；不同种故障模式的样本在映射到决策平面后，其在平面内的距离较远。说明本文方法有效的降低了故障样本从高维到低维映射时产生的畸变。

图5 SOM对轴承数据的聚类结果

图6 本文方法对轴承数据的聚类结果

Fig.6 The proposed method clustering of the rolling bearing data

评价聚类结果优劣的过程称为聚类有效性分析，过程中所使用的指标称为聚类有效性指标。一个好的聚类方法应尽可能反映数据的内在结构，使类内样本尽可能相似，类间样本差异尽可能大[26]。DB(Davies-Bouldin)指标是基于样本的类内散度与各聚类中心间距的测度。

(8)

式中：DWi为聚类Ci的所有样本到其聚类中心的平均距离;DCij为聚类Ci和聚类Cj中心之间的距离;k为k个聚类。由式(8)可以看出，DB指标的数值越小，表示聚类效果越好。计算得SOM聚类有效性指标DB值为0.690 6，本文方法的聚类有效性指标DB值为0.351 9。本文方法的DB值比SOM方法的DB值减小了49.04%。

由于SOM聚类方法需要对输出层各权向量赋随机数进行初始化，在随后的迭代过程中，是通过调节权值来使神经元与输入向量更加匹配，所以故障样本所激活的神经元的位置是不可预知。因此权值向量初始化的不同将会导致最终聚类结果的不同。在本文方法中，通过计算样本之间的相互影响调节样本的位置，从而使故障样本在决策平面的位置坐标收敛，因此故障样本总能在决策平面收敛到相对固定的位置。本文方法的这些特点保证了算法输出结果的确定性，即多次训练后不同故障模式在决策平面的最终的相对位置是固定的。图7是多次运行的某次聚类结果，对比图6和图7发现，将图7向右旋转90°之后，两图中各故障模式之间的相对位置相同。

图7 本文方法对轴承数据的特征的聚类结果

Fig.7 The proposed method clustering of the rolling bearing data

4 柴油机振动测试实验

柴油机振动测试实验的实验数据来源于新加坡国立大学小波近似和信息处理中心[27]。柴油机为ISUZU C240型四冲程四缸柴油机。交流发电机和电力负载箱与柴油机相连为其提供载荷，信号采集使用B&K的4393型加速度传感器和2635型电荷放大器。采样频率为20 kHz，采样过程由安装在发电机轴末端的编码器触发。实验过程中柴油机转速1 800 r/min，所加载荷为最大载荷的40%。在第四缸模拟了四种运行状态：缸套和活塞环磨损造成的漏气；喷油嘴阻塞造成的喷油压力过大，喷射压力为160 kg/cm2；针阀和喷嘴磨损造成的喷油压力过小，喷射压力为80 kg/cm2；喷油压力正常，喷射压力为120 kg/cm2。

实验分析数据为柴油机一个工作循环周期0.067 s的振动信号。每种状态的数据采集30组，共有120组数据。提取8维数据特征作为本文方法的输入，决策平面大小为11×11，势能函数选为线性函数E=|s-d|。使用本文方法对柴油机四种状态的振动信号的聚类结果如图8所示，图中椭圆图形是为了方便观察而加上的。其聚类有效性指标DB值为0.150 6。从图中可以看到四种状态的信号被很好的区分开，并且同种状态的样本在决策平面上的位置较近，不同状态的样本在决策平面上被放置到了较远的位置。不仅如此，本文方法在映射的同时还能保持故障样本在原样本空间的距离关系。由势能函数E=|s-d|可知，当样本间的相似性度量d较小时，势能函数的最小值点在距离较近的位置；当样本不相似时，即相似性度量d较大时，势能函数的最小值点在距离较远的位置。该方法在确定样本在决策平面上的位置时，不仅考虑了相似样本间相互关系，而且考虑了不相似故障样本间的相互关系，因此该方法能够保留不同类型故障样本间的距离信息。

图8 本文方法对柴油机振动信号聚类结果

图9所示为使用PCA对柴油机四种类型状态振动信号的特征降至2维。其聚类有效性指标DB值为0.158 2。将PCA应用于聚类分析时，其在力保数据信息丢失最小的原则下，将数据从高维变量空间映射到低维变量空间[28]。对比图8和图9可以发现，两张图中不同故障类间的相对位置是相同的。说明本文方法在聚类时不仅能够将相似的样本聚集到一起，而且能够保留不同样本间的相对位置信息。

图9 主分量分析聚类结果

5 结 论

本文分析了无监督聚类算法存在的一些问题，针对这些问题，提出了一种基于分子结构设计理论的聚类分析方法，并给出了其原理和算法。将本文提出的方法应用于滚动轴承振动数据的聚类中，相比于使用SOM聚类算法，本文方法将聚类有效性指标DB值降低49.04%。将本文方法应用于柴油机振动数据的聚类中，实验结果表明聚类效果良好，本文方法能够有效地应用于故障模式的聚类，并得到结论如下：

(1) 本文方法有效的降低了故障样本从高维到低维映射时产生的畸变。

(2) 本文方法不需要事先设置聚类数等初始参数，避免了初始参数的设置对聚类结果的影响。

(3) 本文方法在聚类过程中，对相似数据聚类的同时，保留不同样本间的相对位置和距离信息。