核磁共振陀螺磁屏蔽罩内静磁场系统优化设计

李 攀，刘元正，严吉中，张 伟

（1. 航空工业西安飞行自动控制研究所，西安 710065；2. 驻210研究所军事代表室，西安 710065）

核磁共振陀螺（Nuclear Magnetic Resonance Gyroscope, NMRG）是一种利用核磁共振原理工作的全固态陀螺仪[1-3]。它没有运动部件，性能由原子材料决定，理论上动态测量范围无限，综合运用了量子物理、光、电磁和微电子等领域中的技术，是未来陀螺仪发展的新方向[4-5]。原子自旋可以在惯性参考系中保持其初始指向，类似于传统机械陀螺中的转子，所以原子自旋也可以用于敏感转动。欧美国家从20 世纪60 年代就已经开始研究核磁共振陀螺，Litton 公司和 Singer-Kearfott公司在 1979 年分别开发出了核磁共振陀螺原型机，均达到了导航级精度[6]。

进入 21 世纪以来，微型原子器件的显著进步证实了原子MEMS 的可行性[7]。2005 年，美国国防先进研究计划局（DARPA）提出了导航级集成微陀螺（NGIMG）概念，在定位、导航和授时微技术（Micro-PNT）项目中对美国 Northrop Grumman 公司的核磁共振陀螺研究给予了支持[8]。到2012年，美国Northrop Grumman公司实现了导航级核磁共振陀螺工程样机的研制，其零偏稳定性达到0.01 (°)/h，成为目前世界上体积最小的导航级陀螺，标志着高精度、小体积陀螺技术领域取得了突破性研究进展[9]。

核磁共振陀螺利用检测磁场中原子核自旋进动频率的改变确定载体角速度。该陀螺所涉及的磁场包括纵向静态磁场和横向振荡磁场，原子核自旋绕静磁场进动，振荡磁场频率与原子核进动频率相同。在进行陀螺设计时，必须保证静态磁场纵向分量在气室范围内均匀分布，横向分量近似为零，振荡磁场横向分量在气室范围内均匀分布，纵向分量近似为零。从陀螺原理可以看出，核磁共振陀螺的陀螺精度与静磁场的均匀性、稳定性密切相关，进行核磁共振陀螺静磁场设计方案分析很有必要。

目前，在核磁共振领域得到工程应用的均匀磁场产生方案一般有两种：1）亥姆霍兹线圈，这是目前商用核磁共振仪常用的磁场结构，缺点是在特定范围内产生均匀磁场所需的线圈尺寸过大；2）螺线管，该结构能够在较小的体积内产生均匀度高的磁场，是核磁共振陀螺工程化生产所需的理想磁场结构。基于上述论断，本文主要研究利用螺线管产生均匀磁场。

1 理论分析

1.1 载流环形线圈的磁场

载流环形线圈如图1所示。以线圈中心为坐标原点建立直角坐标系，z轴与线圈平面垂直，电流I以逆时针方向绕z轴旋转。根据毕奥-萨伐尔-拉普拉斯定律，线圈上任一长度dl处电流元Idl在点P形成的磁场可以表示为

图1 环形电流磁场Fig.1 Ring current magnetic field

其中，r为元电荷指向点P的矢量，μ0为真空电导率。

由于线圈具有轴对称特性，可以将点P放置在xz平面上以减少计算步骤。考虑位于S点的电流元Idl，OS与x轴的夹角为φ，则有：

由图1可知：

将式(2)(3)代入式(1)可得：

化简，可得：

若点P位于z轴上，则θ=0，r0=z，于是：

1.2 通电螺线管的磁场

为顺应核磁共振陀螺微小型化的发展趋势，核磁共振陀螺所使用的螺线管通常用挠曲电路工艺制造——先采用双层挠曲电路工艺将线圈制造在一个平面基底上，再将挠曲线圈卷成圆柱形，形成螺线管，如图2所示(加州大学Irvine分校，2008)[10]。

这种方法形成的螺线管是疏绕螺线管。设螺线管长为L，半径为R，单位长度的匝数为m，电流强度为I。螺线管的磁场基本可以看作一系列圆形线圈磁场的叠加。考虑轴线上某点O的磁感应强度，取该点为坐标原点，Oz沿轴线并与电流方向满足右手定则，如图3所示。

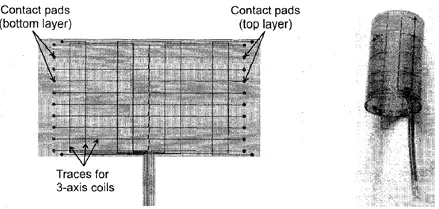
图2 使用平面挠曲电路制造的三轴线圈Fig.2 Three-axis coils fabricated on planar flex circuit

图3 螺线管轴上的磁场Fig.3 Magnetic field on the solenoid axis

在位置z处长度dz内共有mdz匝线圈，它在原点产生的磁感应强度只有z方向分量，由式(6)可以得到其大小为：

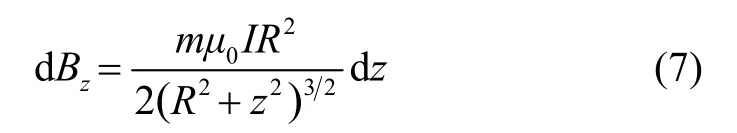
整个螺线管在原点产生的磁感应强度为：

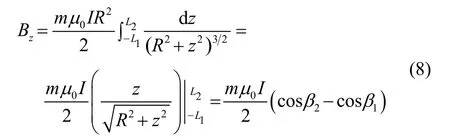
其中，β1和β2如图3所示，为点O与螺线管两端的夹角。

1.3 静磁系统初步设计

国内外对核磁共振静磁系统的研究不多，也未做更深一步的探讨。国内研究机构采用密绕螺线管或亥姆霍兹线圈设计居多[11-14]；而国外研究机构更多采用疏绕螺线管设计[10,15-16]，如图4所示，图中的疏绕螺线管包含横向补偿线圈。

图4 疏绕螺线管（美国普林斯顿大学，2011年）Fig.4 Unwinding solenoid (Princeton University, 2011)

螺线管的常规设计一般只需要关注几项指标，包括螺线管半径、螺线管长度和螺线管的匝数。定义磁场均匀性指标δ=std(B)/mean(B)，取值越小代表磁场越均匀。简单计算可以得到，在常规长径比范围内的螺线管，其磁场均匀性通常满足下列规律：

1） 螺线管半径越大，均匀性越好；

2） 螺线管长度越长，均匀性越好；

3） 螺线管匝数与磁场均匀性无关，但影响磁场大小。

以气室尺寸为4mm×4mm×4mm为基准，结合实际情况和陀螺结构，初步设计螺线管指标为：螺线管半径R=25 mm，长度L=50 mm，总匝数n=5，通电流I=1.3A。取气室尺寸范围内计算磁场均匀性δ=4.27× 10–4，沿z轴的磁场分布如图5所示。

图5 螺线管的磁场分布Fig.5 Magnetic field distribution of the solenoid

2 磁屏蔽罩对陀螺静磁场均匀性的影响

在典型的实验室磁场（1～10 T）中，核磁共振陀螺中工作原子的核自旋对应的拉莫尔频率大多数情况下在10～100MHz量级内[17]。这个数值必须与用核磁共振陀螺检测的典型旋转速度相匹配，以地球自转速率为参考ωearth=7.27×10−5rad/s，此旋转速率大约比典型的实验室中的普通拉莫尔频率小12～13个数量级。如果核磁共振陀螺需要检测出低于地球自转3～4个数量级的角速度，则静磁场数量级要求更低。为保证静磁场的稳定性，防止外部磁场的干扰，必须对核磁共振陀螺进行磁屏蔽[18]。

由于核磁共振陀螺磁屏蔽罩通常由高磁导率（>104）的软铁磁材料制造，通电电流会在材料表面形成感生磁场。根据静磁场的惟一性定理，可以将螺线管磁场在磁屏蔽罩端面产生的磁化电流等效为“磁像”的虚拟电流，类似于镜面。由于磁屏蔽罩和其内螺线管安装的实际情况，磁力线会在磁屏蔽罩两端面之间来回反射，可以用多轮迭代的方法来计算。对于一轮迭代（对应反射一次），其磁场相当于3个螺线管的叠加，如图6所示；对于两轮迭代（对应反射两次），磁场相当于5个螺线管的叠加，以此类推。为便于计算，假设螺线管完美排列，磁屏蔽罩屏蔽因数无限，此时“磁像”的虚拟电流不发生衰减。

图6 磁力线在磁屏罩内反射一次Fig.6 Magnetic lines reflecting once in the magnetic shield

综合考虑计算精度和计算效率，计算过程共进行100轮迭代，计算201组螺线管。继续增加迭代数量对计算结果贡献不大，因为此时的“磁像”螺线管距离计算区域过远。螺线管指标暂定为R=25 mm、L=50 mm、n= 5、I=1.3 A，螺线管距磁屏蔽罩的距离d=5 mm，此时d=1.453×10-4，沿z轴的磁场如图7所示。可以看出磁屏蔽罩对螺线管产生磁场的均匀性有所改变。

图7 磁屏蔽罩改变了螺线管的磁场分布Fig.7 Effects of the magnetic shield on magnetic field distribution

固定其余参数并分别改变螺线管端面距磁屏蔽罩距离d、螺线管匝数n、螺线管长度L和螺线管半径R，以确定单一结构参数对螺线管产生磁场的均匀性δ的影响，如图8所示。

图8中的 (a)(b)(c)(d)图分别为螺线管端面距磁屏蔽罩的距离d、螺线管线圈匝数n、螺线管长度L和螺线管半径R对磁场均匀性d的影响。从图8的(a)(b)(c)中可以看出，磁场均匀性的极小值点分别出现在d=6.15 mm、n=6、L=40 mm点，其共同特征是此时线圈距磁屏蔽罩的距离大致等于线圈间距一半。简单推论易知，理想情况下磁屏蔽罩端面会将有限长疏绕螺线管扩展到无限长，此时磁场均匀性δ=0。然而，图8(a)中d=6.15 mm并不严格等于线圈间距的一半6.25 mm，图8(c)中在L=72 mm处又出现了一个极小值点。而图8(d)中磁场均匀性随着螺线管半径R的增大，总的来说逐渐减小，但在R=19 mm处出现了一个极小值点，这是由于计算磁场均匀性的取样范围有限，如果将取样范围扩大（如图9所示），此时最优点就逼近理论值，即螺线管端面距磁屏蔽罩的距离d大致等于线圈间距一半。

图8 螺线管参数对磁场均匀性的影响Fig.8 Effects of the solenoid parameters on magnetic field uniformity

从图9中可以得出另一个结论，对于有限长螺线管，通过将线圈间距从等间距改变为不等间距可以在一定区域内进一步优化磁场均匀性。

图9 大取样范围下的磁场分布Fig.9 Magnetic field distribution over a large sampling range

3 螺线管结构参数加工误差分析

考虑到实际使用情况，确定螺线管设计指标为：线圈半径R=25 mm，长度L=50 mm，匝数n=5，螺线管端面距磁屏蔽罩的距离d=6.152 mm，螺线管通的电流I=1.3A。取气室尺寸范围内计算磁场均匀性d=1.10× 10–7。沿z轴的磁场如图10所示。

图10 改进螺线管的磁场分布Fig.10 Magnetic field distribution of the improved solenoid

如图11(a)所示，磁场均匀性d随A的绝对值的增大线性增加，在零位两侧近似对称。

再考虑螺线管与屏蔽罩中心对准误差B，此时螺线管两端距磁屏蔽罩的距离为dB+。从图11(b)中可以看出，与误差A类似，磁场均匀性d随B的绝对值的增大线性增加，在零位两侧近似对称，但B对磁场均匀性d的影响比A大致高了一个量级。

图11 螺线管加工误差对磁场均匀性的影响Fig.11 Effects of the solenoid’s machining errors on magnetic field uniformity

最后考虑疏绕螺线管间距存在加工误差C，该误差与上述两个误差A和B无法完全分离，所以将其综合在一起分析。对螺线管各线圈的位置随机加减一个不大于C的数，进行多轮计算（1000次）后取其最大值（最差值），来判断C对磁场均匀性d的影响。

从图11(c)中可以看出，磁场均匀性d随C的增大线性增加。

综合考虑实际加工、装配难度和磁场均匀性要求，确定螺线管加工误差限为 0.01 mm，此时磁场均匀性d≤ 1.11×10–5（均值 3.69×10–6），较优化前至少提高了一个量级。

4 结 论

作为一种新型微型陀螺仪，随着MEMS技术和微型原子器件的发展，核磁共振陀螺仪有望在中低精度导航和制导领域得到应用，其潜在应用方向包括小型飞行器、无人飞行器、无人水下潜艇、地面车辆、战术导弹等。本文从核磁共振陀螺静磁场分布的理论分析出发，通过数学计算和计算机仿真，分析和研究了磁屏蔽罩对静磁系统的影响，通过综合调整螺线管与屏蔽罩的交互参数，对静磁系统进行了优化设计，同时还确认了加工误差对系统性能的影响。设计的核磁共振陀螺静磁系统磁场优于 1.11×10–5（均值3.69×10–6），较优化前提高至少一个数量级，满足核磁共振陀螺的使用需求。该工作为核磁共振陀螺仪设计和制造提供了一定的理论依据和参考价值。