高超声速机动目标的强跟踪UKF自适应交互多模型算法

戴洪德，方 君，唐 亮，王希彬

（1. 海军航空大学，航空基础学院，烟台 264001；2. 海军驻汉中地区航空军事代表室，汉中 723213；3. 91213部队，烟台 264007）

一直以来，机动目标跟踪都是目标跟踪领域的难点问题[1]。而超高速强机动目标，如美国陆军与桑迪亚国家实验室联合发展的“先进高超声速武器”（AHW），期望能够在 30 min内打击地球任意目标，平均速度达到近 10 Ma。相对常规目标，这类高机动目标具有多种运动状态，而且各运动状态间的切换更复杂、更突然，快速高精度跟踪的难度也就更大。虽然学者们提出了很多单模型算法并进行了一系列改进，但单一的模型不可能描述高机动目标的所有运动状态，当运动状态和模型差别较大时，就会导致目标跟踪滤波器发散，目标跟踪失败[2-3]。

针对以上存在的问题，文献[4]以广义伪贝叶斯算法为基础，提出了交互多模型算法（IMM），较好地解决了单模型算法存在的滤波器发散等问题。之后学者们对IMM算法进行了深入的研究[5-7]，并将其应用于目标跟踪领域。近年来，学者们通过对 IMM 算法性能进行分析，提出了基于模型概率更新的改进算法[8-9]。对常规机动目标而言，这些算法的跟踪精度均有提高，但并不能实现对超高速强机动目标的精确跟踪：一是模型集的选择没有针对性[10]，1997年Kishore借鉴Singer模型，首次提出了Jerk模型算法[11]，文献[12]借鉴“当前”统计思想，提出了“当前”统计Jerk模型，在此基础上学者们提出了一系列改进方法[13-14]，但这些模型还很少被选作 IMM 算法的子模型进行研究；二是 IMM 算法中模型概率与模型匹配度之间仍存在偏差，算法的自适应性不高。

在目标跟踪中，系统模型一般是在直角坐标系下建立的线性模型，而量测数据通常是由定义在极坐标系里雷达系统观测得到的，所以量测模型为非线性模型，必须采用非线性滤波算法进行目标状态的估计。基于非线性模型线性化的扩展卡尔曼滤波（Extended Kalman Filter，EKF）是最早获得成功应用的非线性滤波算法，但对于非线性较强的系统，常常因为线性化带来的误差较大而导致滤波发散。基于UT变换（Unscented Transformation）的UKF（Unscathed Kalman Filter）是对非线性概率密度进行逼近，相比EKF精度更高，但UKF在模型误差、干扰、噪声比较大时，滤波精度和鲁棒性不够。Xia[15]为克服微惯性传感器的大漂移特性，提出了神经网络辅助强跟踪滤波方法，利用强跟踪滤波实现状态预测，利用二阶EKF实现测量更新，结合神经网络技术完成对状态预测的修正。王晓旭等[16]结合强跟踪滤波（Strong Tracking Filter，STF）的思想，由正交性原理，提出了STUKF，文献[17-18]根据强跟踪滤波器成立的充分条件，经推导证明得到改进的STUKF。

本文在前人研究的基础上，针对超高速强机动目标跟踪问题，提出了一种新的 IMM 跟踪算法。首先针对目标的强非线性特点，推导了引入多渐消因子的强跟踪UKF算法；其次合理地选择模型集，将一种改进的CS-Jerk模型引入到IMM算法；最后对标准IMM算法进行改进，利用各个模型的残差向量修正模型转移概率矩阵，避免了由于人为设定马尔科夫矩阵而影响模型之间的交互与切换。仿真结果表明，与标准IMM算法相比，本文提出的IMM算法通过实时更新模型转移概率，改进模型概率更新方法，合理地选择模型集，能够明显提高超高速强机动目标的跟踪精度。

1 基于多重渐消因子的强跟踪UKF算法

1.1 强跟踪UKF

设非线性系统的状态方程和量测方程为：

当滤波器正常工作时，残差具有正交性，而当系统状态发生突变时，残差失去正交性，滤波误差增大。强跟踪滤波器（STF）通过引入时变的渐消因子，在线调整滤波器增益矩阵，使输出残差近似正交。其核心思想就是在线实时调整增益矩阵以满足条件：

文献[17]在对文献[16]分析之后证明，当按照式(4)在中引入渐消因子若状态估计使用未引入渐消因子时的残差则无法保证式(2)成立，若状态估计使用引入渐消因子后的残差则无法保证式(3)成立，基于此得到改进的STUKF算法。本文考虑高超速强机动目标准确建模困难，而且强机动时量测噪声增大的特点，提出进一步改进的STUKF，在滤波过程中只对非线性状态进行一次采样，降低了计算量。在计算误差方差阵时引入多重渐消因子，克服了单一渐消因子忽略不同状态之间差异影响滤波精度的局限性。其步骤如下：

2）确定滤波采样点：

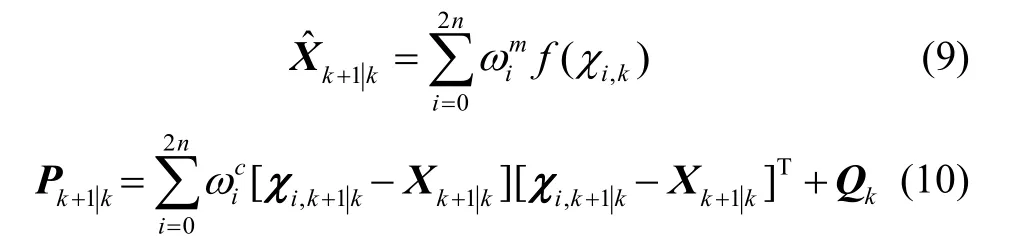
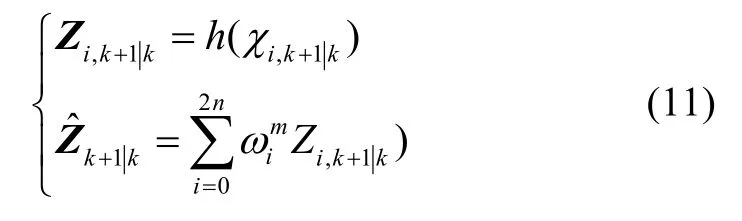
5）计算残差及引入多重渐消因子的量测协方差和互协方差。文献[16]和文献[17]中的强跟踪UKF算法均采用单一的渐消因子，但超高速强机动目标系统模型不确定性更大，对不同状态的影响也不同，采用单一渐消因子难以对每个状态都实现高性能跟踪，多重渐消因子则可以很好地解决这一问题。

与文献[17]中的强跟踪UKF算法相比，本文算法引入多重渐消因子克服了单一渐消因子的局限性，而且只需进行一次UT变换，计算量更小。

1.2 多重渐消因子矩阵的计算

文献[17]中已经推导了单一渐消因子的确定过程，在此基础上，多重渐消因子矩阵的计算方法如下：

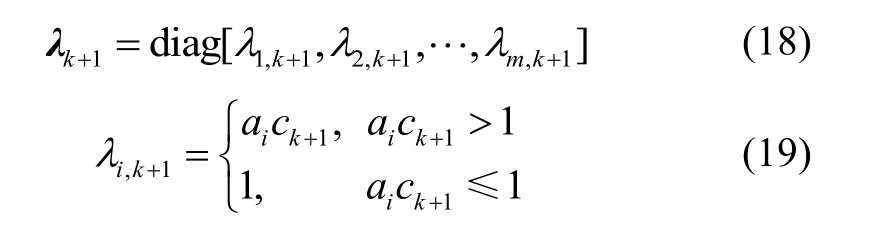
式中：m为观测向量维数；为根据先验信息确定的常数，当量测量噪声变化较大时，较大，否则可均取为1；为根据滤波器性能在线自适应确定的因子，即

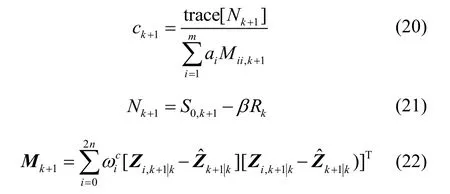
2 STUKF-IMM算法

对于一个超高速强机动目标，由于 IMM 算法中模型数是有限的，模型集中所有模型都不能绝对准确描述目标运动，然而合理的模型集中，任一时刻总有一个模型与目标的匹配度最高，所以模型集的选择必须合理。已有的匀速模型（Constant Velocity，CV）、匀加速模型（Constant Accelerater，CA）、Singer模型、当前统计模型（Current Statistical，CS）以及Jerk模型等均适用于不同的场景，其中，CV、CA适用于目标进行非机动运动的情况，Singer、CS等三维模型能够精确跟踪目标的常规机动，而Jerk模型作为已有的阶数最高的模型，其主要价值是跟踪强机动目标。高速强机动目标在运动过程中，会出现匀速、加速，甚至是加加速等多种运动状态，IMM算法所选择的模型集要尽可能考虑到目标机动的所有情形，尤其是目标高速强机动运动阶段，由于目标以很大的加速度甚至是加加速度机动，与之对应的子模型也应该更符合实际情况。

2.1 基于假设检验的参数自适应CS-Jerk模型

文献[12]已经证明，相比Jerk模型，CS-Jerk模型更能有效跟踪目标的强机动，但是 CS-Jerk模型中，目标的机动频率、极限机动加加速度必须要预先设定，根据这些值来确定过程噪声协方差阵，当目标机动频率和极限加加速度变化时，该模型会产生较大的模型误差。

本文提出一种参数自适应 CS-Jerk模型，并作为IMM算法的子模型之一。自适应调节一般都是基于滤波新息的闭环过程。目标机动反映在滤波结果中是新息向量的变化，而反映在状态方程中就是状态转移矩阵和状态噪声协方差阵的变化。改进的模型由新息向量构造活化函数[19]，生成活化因子，实时修正目标的机动频率和最大、最小机动加加速度以实现状态转移矩阵和状态噪声协方差阵随目标机动自适应调整。

由文献[20]可知，n维高斯随机向量的协方差矩阵的迹是自由度为n的分布。新息向量为其协方差矩阵为当目标不发生机动时，新息向量为零均值的高斯白噪声；当目标机动时，新息向量的正交性被改变，不再服从零均值高斯分布。目标跟踪过程中，根据新息协方差矩阵的迹来判读目标跟踪滤波器是否正常，具体步骤为：

1）模型匹配时新息协方差矩阵的迹服从自由度为m的

2）假设检验准则为：

4）活化因子的引入函数如下：

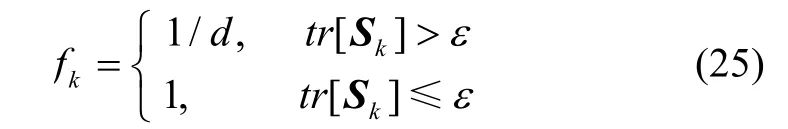
这样就可以得到改进模型中机动频率的更新式为

同时，机动加加速度方差的更新式为

2.2 STUKF-IMM算法

交互式多模型算法主要包含四个部分：模型交互输入、滤波计算、模型概率更新、模型输出融合。将STUKF作为IMM算法中的滤波器，即可得STUKFAIMM算法。

其中：第j个模型的系统方程为系统噪声均值为零，协方差矩阵为第j个模型的量测方程为量测噪声的均值为零，协方差矩阵为

交互多模型转移概率矩阵为

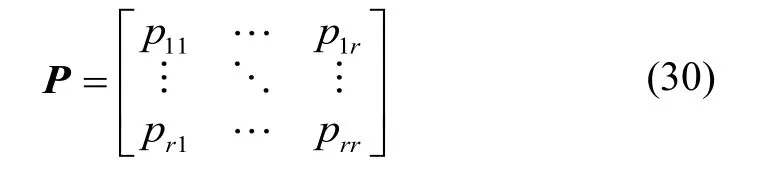
则IMM算法的递推过程为：

1）多模型状态估计融合

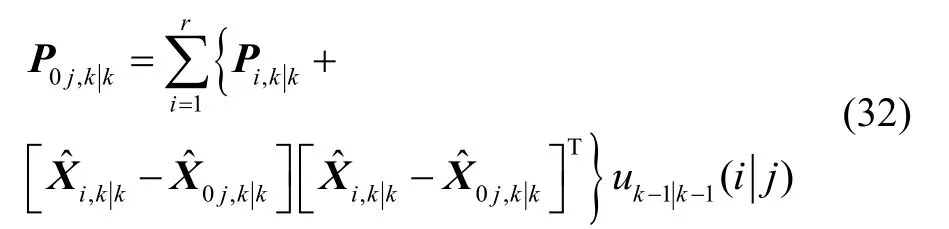
2）状态更新

3）模型概率更新

对于第j个模型，时刻其最大似然函数如下：

模型j对应的后验概率为

4）模型融合输出

3 模型转移概率的实时修正方法

标准的 IMM 算法假定输入交互过程为一马尔科夫过程，模型之间的转移概率服从：

模型转移概率决定着输入交互即模型新一轮初始化的结果，而在标准的交互多模型算法中，转移概率是根据主观判断或先验信息预先设定的，在整个计算过程中保持不变，且假设各子模型的新息序列均为零均值的高斯白噪声，这与实际必然存在偏差。当目标发生机动，运动状态出现突变时，由于预先设定的转移概率与目标实际运动状态不匹配，目标状态的估计就会产生较大的误差。因此，需要寻找一种方法，能够根据目标状态的变化，实时调整各模型间相互转移的概率，以实现对目标的精确跟踪。

为了解决上面提出的问题，本文引入调整因子，对模型的转移概率进行实时自适应调整，残差作为滤波算法中的后验信息，充分反映了目标当前时刻的状态变化。假设IMM算法中有个子模型，时刻个子模型滤波得到的残差分别为。定义残差的范数为：

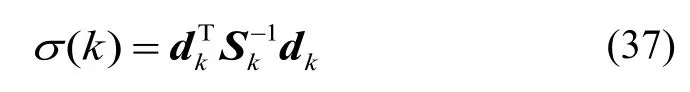
系统由子模型i转移到子模型的概率为进行更新，即：

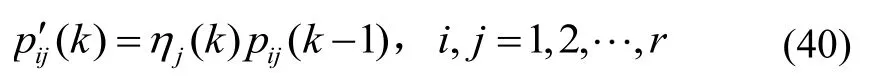
4 仿真验证

选择CA、CS和本文提出的改进CS-Jerk模型作为IMM算法的模型集（对于低维模型，需要进行增广处理），目标初始条件设为目标机动频率的初始值为在CS模型中，x、y方向上的最大、最小加速度分别为在改进 CS-Jerk模型中x、y方向上最大、最小加加速度初始值分别为

采用UKF滤波算法进行蒙特卡罗仿真，仿真次数为100。用目标状态估计值的均方根误差（RMSE）和均值误差（ME）为性能指标来衡量本文提出算法的性能。状态估计值的均方根误差定义为：

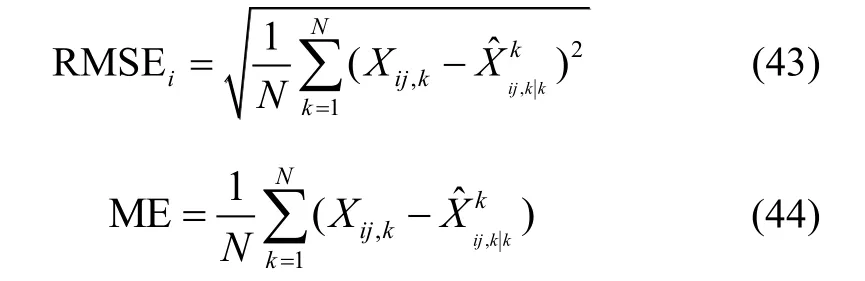
在相同基本条件下，共进行三组仿真实验，分别验证模型集的选择、本文提出的强跟踪UKF算法以及模型概率实时修正方法对IMM算法跟踪性能的提高作用。

仿真1：以CA、CS模型为基础，分别与Jerk、CS-Jerk、本文提出的改进 CS-Jerk模型组成 IMM 模型集，并采用文献[16]中的STUKF进行滤波，对比三种 IMM 算法对目标的跟踪精度。取模型初始概率为马尔科夫模型转移概率矩阵为进行100次Monte Carlo仿真，目标的跟踪轨迹如图1所示，x方向上目标位置和速度估计值的均方根误差曲线如图2和图3所示，y方向上目标位置和速度估计值的均方根误差曲线如图4和图5所示。

分析图2、图3可以发现，引入Jerk模型的IMM算法，其位置、速度均方根误差最大值分别超过400 m和600 m/s；而基于本文提出的改进CS-Jerk模型以及引入CS-Jerk模型的IMM算法目标位置、速度的均方根误差均显著减小，显然本文算法的误差最小。图4、图5表明，在y方向上目标不发生机动时，三种算法的精度相当，但基于改进CS-Jerk模型的IMM算法对目标位置和速度的跟踪精度仍然更高。

图1 估计轨迹与真实轨迹Fig.1 The estimated trajectory and the real trajectory

图2 仿真1：x方向位置均方根误差Fig.2 Simulation 1: the mean square root error of position x

图3 仿真1：x方向速度均方根误差Fig.3 Simulation 1：the mean square root error of velocity x

图4 仿真1：y方向位置均方根误差Fig.4 Simulation 1: the mean square root error of position y

图5 仿真1：y方向速度均方根误差Fig.5 Simulation 1: the mean square root error of velocity y

仿真2：以本文提出的改进CS-Jerk模型与CA、CS模型组成模型集，对比本文设计的多重渐消因子强跟踪UKF与文献[16]中单一渐消因子强跟踪UKF的滤波性能。经过100次Monte Carlo仿真，x、y方向位置和速度的误差见图6～9。结果表明与已有的STUKF算法相比，采用改进的STUKF进行滤波计算时，x方向上目标状态估计误差相当，y方向上目标状态估计精度明显提高，故本文的滤波算法更好地解决了强非线性滤波问题。

图6 仿真2：x方向位置均方根误差Fig.6 Simulation 2: the mean square root error of position x

图7 仿真2：x方向速度均方根误差Fig.7 Simulation 2: the mean square root error of velocity x

图8 仿真2：y方向位置均方根误差Fig.8 Simulation 2: the mean square root error of position y

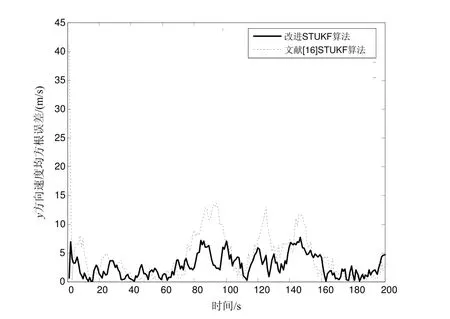
图9 仿真2：y方向速度均方根误差Fig.9 Simulation 2: the mean square root error of velocity y

仿真3：选择改进CS-Jerk模型与CA、CS模型组成模型集，应用于本文提出的自适应 IMM-STF-UKF算法中。对比模型概率和模型转移概率矩阵取不同的初始值时，自适应IMM算法与标准IMM算法跟踪性能。假设有初始条件：

真，表1、表2分别为三种初始条件下x、y方向上状态估计值的均值误差。

表1、表2的仿真结果表明，在仿真1和仿真2的基础上，若采用标准的 IMM 结构，当初始条件为条件2时，目标的跟踪精度最高；而采用自适应IMM结构时，在三种初始条件下，x方向上目标位置估计值的平均误差分别减小了 22.9%、12.05%和 12.33%，速度估计值误差分别减小19.34%、11.89%、14.54%；y方向上目标位置跟踪的平均误差分别减小了20.99%、16.61%和27.74%，速度跟踪平均误差分别减小42.52%、35.74%、47.91%。

表1 仿真3：x方向上目标状态估计值的平均误差Tab.1 Simulation 3: the mean error about state of target in x

表2 仿真3：y方向上目标状态估计值的平均误差Tab.2 Simulation 3: the mean error about state of target in y

相比标准的IMM算法，自适应IMM算法的跟踪精度明显提高，且在不同的初始条件下目标状态估计值的平均误差相当，减小了预设马尔科夫矩阵对算法跟踪性能的影响。

5 结 论

针对超高速强机动目标的机动具有突发性、强度高、变化复杂，使得跟踪精度降低甚至失败的问题，本文提出了一种基于UKF的自适应交互多模型算法。该算法首先在分析已有强跟踪UKF算法后，提出了新的强跟踪UKF滤波；然后通过分析新息的统计学特性，找到一种改进 CS-Jerk模型的方法；之后针对标准IMM 算法的缺陷，给出模型转移概率矩阵自适应的IMM结构，并实现了改进CS-Jerk模型与自适应IMM结构的有机结合。改进 CS-Jerk模型能够实现对目标强机动阶段更准确地建模，而自适应 IMM 结构克服了标准 IMM 算法马尔科夫矩阵预设不准确，且先验确定难度大的问题，这两者的结合为研究超高速强机动目标的跟踪提供了一种新思路。计算机仿真表明，所提出的算法显著提高了高超声速强机动目标的跟踪精度，具有重要的工程应用价值。