移动双弥散信道建模及Matlab仿真测试*

梁 源,达新宇,徐瑞阳,倪 磊,刘慧军,张 喆

(空军工程大学信息与导航学院,西安 710077)

0 引言

由于移动通信具体快速、高效、灵活的特点,一经提出研制并投入商用就获得用户的广泛青睐,给人们的通信与交流方式带来了前所未有的快捷与便利。与此同时,随着人们对于通信语音话质需求的提高,并伴随着图片、视频等业务类型多样性需求,移动通信对于传输数据的带宽、载体移动性、传输效率等方面提出了更高要求。特别是,目前正紧锣密鼓研制中的5G移动通信,作为其三大基本定义场景之一的“增强移动宽带”(EMBB,enhanced Mobile Broadband),对于数据速率及抗载体移动、抗信道多径提出了更为严苛的要求[1]。

关于移动通信相关技术的研究,很重要的一点就是对于通信环境中信道的研究,结合具体的信道特点采用相应的信道均衡技术来最大程度的减少信道干扰,提升通信系统的可行性。关于移动通信衰落场景,主要可以分为两类:平均路径衰落和阴影衰落引起的大尺度衰落,以及由多径、多谱勒频移引起的小尺度衰落[2]。大尺度衰落在一定的时间与地域具有相对稳定的特点,其分析与计算过程基本保持不变,因而目前关于信道的研究多集中在以多径、多谱勒引起的小尺度衰落上,并且在小地区与短时间范围内呈现了很大差异。针对由多径引起的时延扩展,相应表现为时间弥散特性;以及传播过程各路径中由于相对运动带来的多谱勒扩展,相应表现为频域弥散特性。因而可以将上述小尺度的信道模型统称为双弥散信道模型。

文中旨在对移动双弥散信道进行建模分析,并从频域与基带等效、卷积、滤波等数字信号处理的基本原理出发,并对其Matlab中编程实现进行定性与定量的分析研究,提出通用的移动双弥散信道建模与Matlab仿真技巧。

1 双弥散信道基本建模

对于实际无线信道而言,由于建筑物、高山、丛林等的遮挡、散射、衍射,最终从发射机到接收机的信号实际上是由多条路径组合而成的。通过分析多径合成信号的包络情况,并根据是否存在直视信号,将多径衰落分为瑞利衰落和莱斯衰落,其中瑞利衰落对应无直视信号的情况[3]。

而针对于多径信道,常见的建模类型有抽头时延线模型(tapped-delay line，TDL)模型和基扩展模型(basis expansion model，BEM)[4-5]。由于TDL模型与经典的数字信号处理形式具有一致性,因此文中主要以TDL模型展开分析研究。图1给出了可变时延间隔的TDL模型,[a1(t),a2(t),…,aK(t)]分别是时延[τ1,τ2,…,τK]对应的复系数[3]。由al(t),l=1,2,…,K是关于时间t的函数,因而一般情况下,认为抽头系统都是时变的。

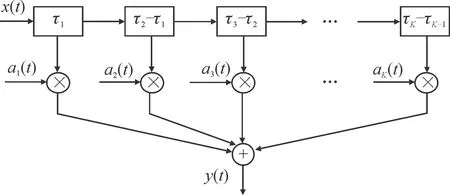
图1 可变时延间隔TDL基本模型

图1对应信道瞬时冲激响应c(τ,t)表达式为:

(1)

从而输入信号x(t)经过信道c(τ,t)得到输出y(t)的表达式为:

(2)

由于实际过程中,时延[τ1,τ2,…,τK]对应不一定是系统采样周期的整数倍,因而在实际处理过程中必须进行相应的等效处理来使得最终的抽头时延等效在整数倍周期采样点上。由文献[6]可知,利用sinc函数的内插处理可以实现这一目的。从而可以得到等效抽取系数gn(t)的表达式为:

(3)

此处,B为等效基带信号带宽,B=1/TS,sinc是采样函数,且sinc(·)=sin(π(·))/(π(·))。理论上,当n取-∞至+∞范围的整数时,gn(t)与ak(t)在实现功能上可以完全等效,但是考虑实际情况,只要在精度允许范围内。可令n∈[-N1,N2],且n为整数,gn(t)在n小于-N1或大于N2时取值足够小即可。这样图1中的可变时延扩展模型就转化成了图2中的固定间隔周期采样抽头线模型。

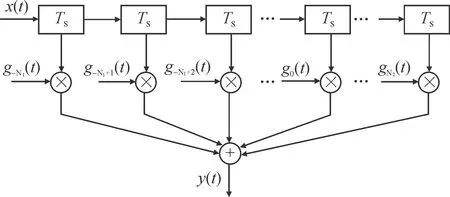
图2 等效固定时延间隔TDL基本模型

图2中输出y(t)与输入x(t)的对应关系式为:

(4)

式中：*表示卷积符号；(τ,t)为瞬时冲激响应,满足如下表达式:

(5)

由上述关于双弥散信道的基本模型及理论公式可知,关于双弥散信道的研究重点在于对其冲激响应的研究,而冲激响应又与TDL时延系统直接相关。

2 信道等效处理及Matlab仿真思路

通过上一节中关于TDL建模及输入输出的理论分析,特别是结合图2与式(4)的研究分析可知,关于信道的实际处理过程可以对应转化为周期采样点上数字信号的处理过程。下面通过实际的Matlab处理技巧,结合带通与低通复等效过程、卷积定理在数字信号处理的具体实现两方面,来进一步论证Matlab的仿真理论基础。

2.1 带通与低通复等效

令x(t)表示中心频域为fc的频带信号,xbase(t)对应为其等效基带信号[7]。相应根据带通信号低通复等效原理,存在如下关系式:

(6)

从式(6)可知,除了载波参数fc以外,xbase(t)包含了x(t)中包括幅度、相位的全部有用信息。与信号复等效对应的是系统复等效,如式(7)所示为输入信号经过冲激响应为h(t)的系统得到输出信号y(t)的过程[8]:

y(t)=x(t)*h(t)

(7)

x(t)、h(t)和y(t)分别是原始数据信号、信道冲击响应、经过信道处理的输出信号。频带卷积定理的等效基带形式为[9]:

ybase(t)=xbase(t)*hbase(t)

(8)

式中：xbase(t)的表达式如式(6)所示；hbase(t)和ybase(t)的表达式如式(9)、式(10)所示:

(9)

(10)

且式(9)、式(10)中的希尔波特变换及载波形式及基本运算符号与式(6)中具有一致性。

上述关于频带信号与基带信号的复等效及其卷积定理的复等效分析,说明了Matlab中基带等效仿真是合理可行的。且在理想情况下,基带处理与频带处理过程完全等效。

2.2 信道处理的Matlab仿真思路

考虑到实际通信信号处理以离散信号处理为主,而卷积形式与有限冲激响应(finite impulse response,FIR)滤波器具有一致性,并且可以利用Matlab中分母项为1,分子项为信道复系数的滤波器来等效实现[10]。filter的等效结构如图3所示。

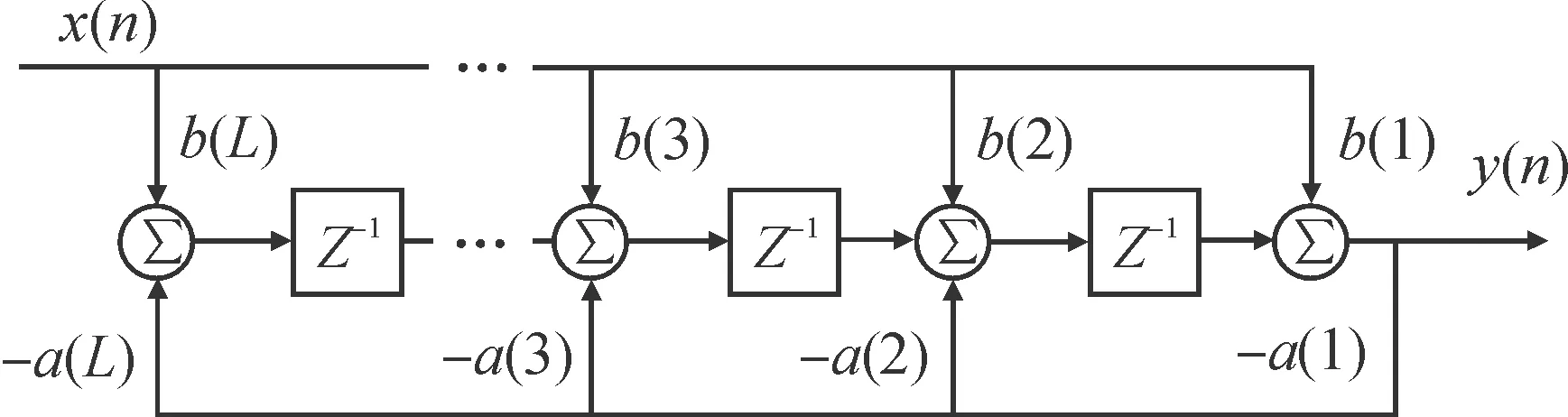
图3 数字滤波器结构示意图

从数字信号处理角度分析,对应z变换域的输入输出关系式为:

(11)

其中,z为相应变换域的基本符号,且满足z=e(-j2π/N)。与FIR结构相一致。

由图1及图2可知,相应的实现过程实则为一特定情形的FIR滤波器,且滤波器的分母系数为1,则相应的信道分析过程,对于输入信号x经过信道系数为chan的衰落信道,则可以利用filter(chan,x)来实现(此处调用filter,默认了分母项系数恒为1)。结合TDL模型结构特点,且可以利用filter进行卷积处理。对于连续时间信号,结合式(7),由卷积定理可以得出相应的频域与表达式为:

Y(jω)=X(jω)H(jω)

(12)

其中,X(jω)、H(jω)和Y(jω)分别是x(t)、h(t)和y(t)的连续傅里叶变换。

而在实际的数字信号处理过程,卷积定理的描述为:“循环卷积对应频域相乘”[11],即具体实现如式(13)、式(14)所示:

(13)

式中：○N表示N点循环FFT变换符号；(·)〈N〉表示数据的N点循环右移。

Y(k)=X(k)H(k)

(14)

由式(12)与式(14)的形式可知,时域上的卷积对应频域上的相乘,这说明频域上进行信道均衡可以将复杂的卷积形式利用乘法来等效实际。卷积定理的提出及使用,为信道均衡提供了一种简单易行的实现方案,在第3部分的试验3中予以详细的仿真测试论证。同时,该方案也为信道估计提供了一种简单易行的解决方案。

综合上述关于带通与低通复等效的关系,以及FIR滤波器与卷积及卷积定理的定量关系式,可以推知利用Matlab进行信道衰落及性能分析的基本处理思路。由于Matlab自带的模块化编程工具Simulink与Matlab代码编程具有一致性,只是在Simulink中用户能够更加直观而简便的调用各种接口与参数而已[12-13]。因此,下面仅从Matlab代码层面以rayleighchan代表的瑞利信道阐明仿真测试分析基本思路:

1)信道复系数的设计

结合双弥散信道的具体时延向量tau(以s为单位)及延时功率分布特点得出的时延对应信号功率pdb(以dB为单位),并结合实际通信系统中最大多谱勒时延fd、系统采样周期ts,最终利用函数h=rayleighchan(ts,fd,tau,pdb)来产生与tau维数相一致的多径系数。需要注意的是,此处产生的系数是与式(2)中ak(t)相对应的系数。pdb一般由时延功率谱决定,且以指数或者均匀分布的最为常见[14]。

2)对输入信号x进行衰落处理

y=filter(h,x),此处调用filter函数,默认产生的复系数h作为FIR滤波器(如式(11)所示)的分子项系数,而分母项系数默认只有a(1),且a(1)=1。

3)结合卷积定理进行信道估计及均衡处理

利用式(13)与式(14)对应的处理技巧,对于衰落进行估计,从而完成信道估计及进行后续的信道均衡等操作。

3 Matlab仿真测试

为了验证图中时延采样模型及等效基带复处理,以及Matlab中利用filter及卷积定理进行相关的仿真处理的正确性,结合第2部分关于双弥散信道的具体处理思路,进行了如下3个仿真实验。下面3个仿真实验都以瑞利衰落为通信场景,且默认采用jakes的功率谱分布形式。

试验1抽头系数等效变换

仿真条件:

数据速率:50 Kbit/s,最大多谱勒频移:80 Hz,单次测试数据长度为500,基带调制方式为2PSK。令多径时延不为采样间隔整数周期倍,对应的时延与衰落因子分别是:[0 2.3e-5]s,[-3 -3]dB,则信道具体函数形式为:

c1=rayleighchan(5e+4,80,[0 2.3e-5],[-3 -3])

结果分析:

利用Matlab自带的图形用户接口(graphical user interface,GUI)工具进行信道性能测试分析[15],图4给出了相应冲击响应(impulse response,IR)幅度的分布图。由于此时多径时延不为采样间隔整数周期倍,因而在带限情况下的等效点取值是实际IR点对应的sinc函数内插求和[16],其中求和的长度为实际IR点数(此处为2),内插sinc的范围是带限等效点数(此处为10)。

为了进一步论证图4结果的正确性,对试验1的c1处理数据前后的结果进行定量分析。表1与c1对应,并对x、y分别对应c1信道处理前后的数据,分别取28、29个数据点对应的信道IR参数,得到的信道IR点组分别为[h1(28)h2(28)]、[h1(29)h2(29)]。g(27)、g(28)是[h1(28)h2(28)]、[h1(29)h2(29)]分别对应的带限等效点取值,此时g(27)、g(28)都是包含10个元素的数组。利用式(13)中卷积运算来求解等效的输出:

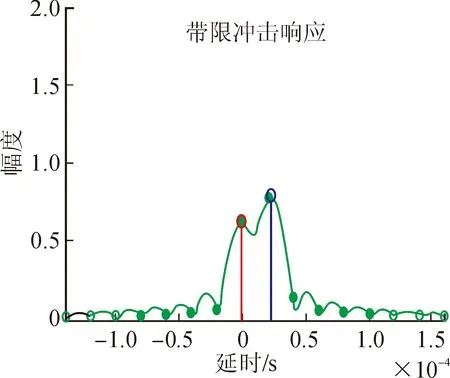
图4 信道冲激响应幅度谱

(15)

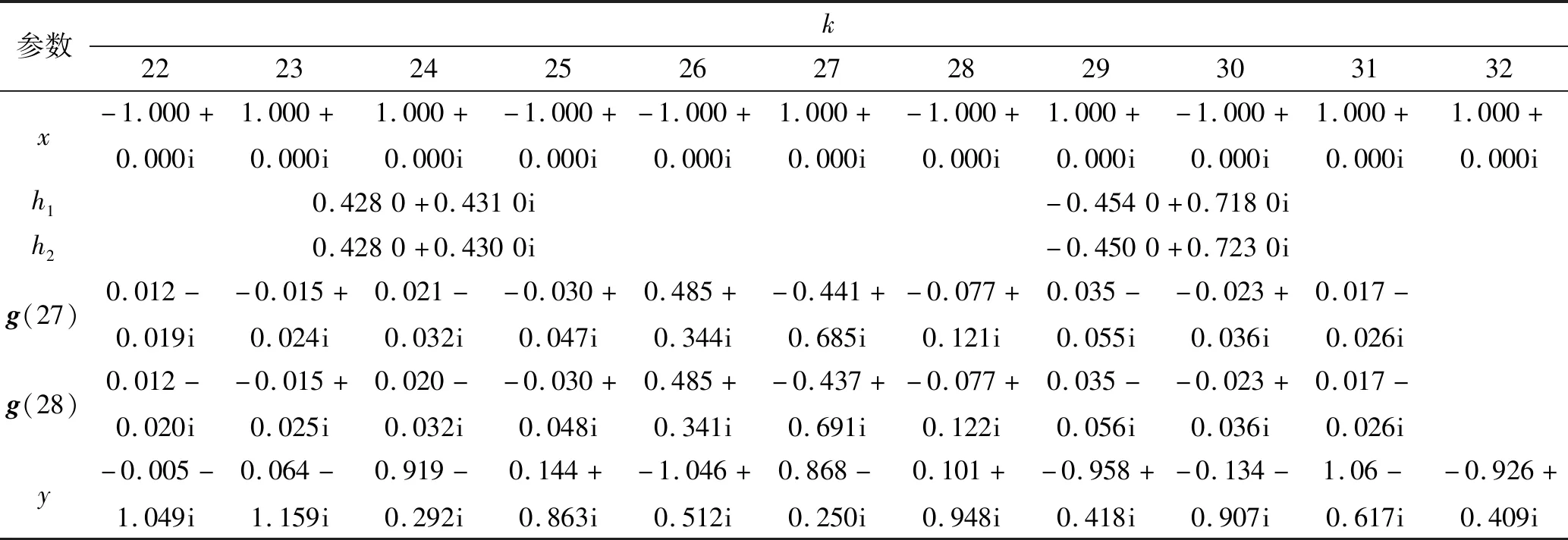
表1 时延为整数倍周期采样时衰落处理结果

试验2理论衰落特性验证

仿真条件:

利用Matlab自带的berfading调用2DPSK基本模式进行理论衰落信道曲线性能测试,而其仿真的前提是认为两个符号之间的衰落变化很微小,即相应信道复系数变化不大[14]。为了使得单个处理符号内的数据满足准静态过程,即令1/(fd×100×bitRate)始终为1,从而令数据速率为bitRate=20 Kbit/s,最大多谱勒频移fd=200 Hz,进而准静态过程维持在一个符号间隔内,此处,信噪比取值范围是:EbN0=[0∶2∶20]dB。

结果分析:

相应仿真结果如图5所示,由于1/(100×fd)=1/(20 000)时间内对应系统的准静态过程,而信号传输的符号率为20 000 bit/s,这样相应的两个符号内可以认为衰落变化非常缓慢,从而满足Matlab中berawgn关于2DPSK“两个符号之间的衰落变化很微小”的前提假设,从而图5中实测得到的误比特率(bit error rate,BER)性能与理论的性能基本一致。

图5 2DPSK衰落性能对比图

试验3OFDM双弥散信道估计与频域均衡

仿真条件:

采用文献[17]中的典型城市(typical urban,TU)衰落场景,时延向量为tau=[0 0.2 0.4 0.6 0.8 1.2 1.4 1.8 2.4 3.0 3.2 5.0]×10-6s,延时功率谱向量为pdB=[-4 -3 0 -2 -3 -5 -7 -5 -6 -9 -11 -10]dB;仿真帧数Nfrm=10 000,信噪比EbN0=[0∶2∶30]dB。一个OFDM符号长度为64(即IFFT变换长度为64),循环前缀(cyclic prefix,CP)长度为16,其总长度为80。在单次循环中每6个OFDM符号前面插入一训练符号(为相应的频域信号形式)用于进行信道估计,同样相应添加长度为16的循环前缀。循环前缀一方面是为了克服OFDM符号间的干扰,另一方面为了使得卷积变成循环卷积。OFDM符号速率为10 000帧/s;则相应的系统采样周期为:1/(80×10 000)=(1.25e-6)s。通过分析可知该情况下,循环前缀的总时间长度大于多径的最大时延长度。对于解调过程的均衡采用最小均方误差(MMSE,minimum mean square error)方式。基带调制方式选用QPSK和16QAM。

结果分析:

为了分析多谱勒频移对于确定信道模型下系统接收性能的影响,分别取多谱勒频移fd=[10 60]Hz,得到最终的接收性能如图6所示。从图6结果可知,对于不同的基带调制方式,在相同的通信场景下,QPSK的抗双弥散干扰性能要优于16QAM,这主要是因为从基带星座图角度考虑可知,16QAM星座点间的等效距离要大于QPSK,因而16QAM具有的抗噪声及干扰能力更差。

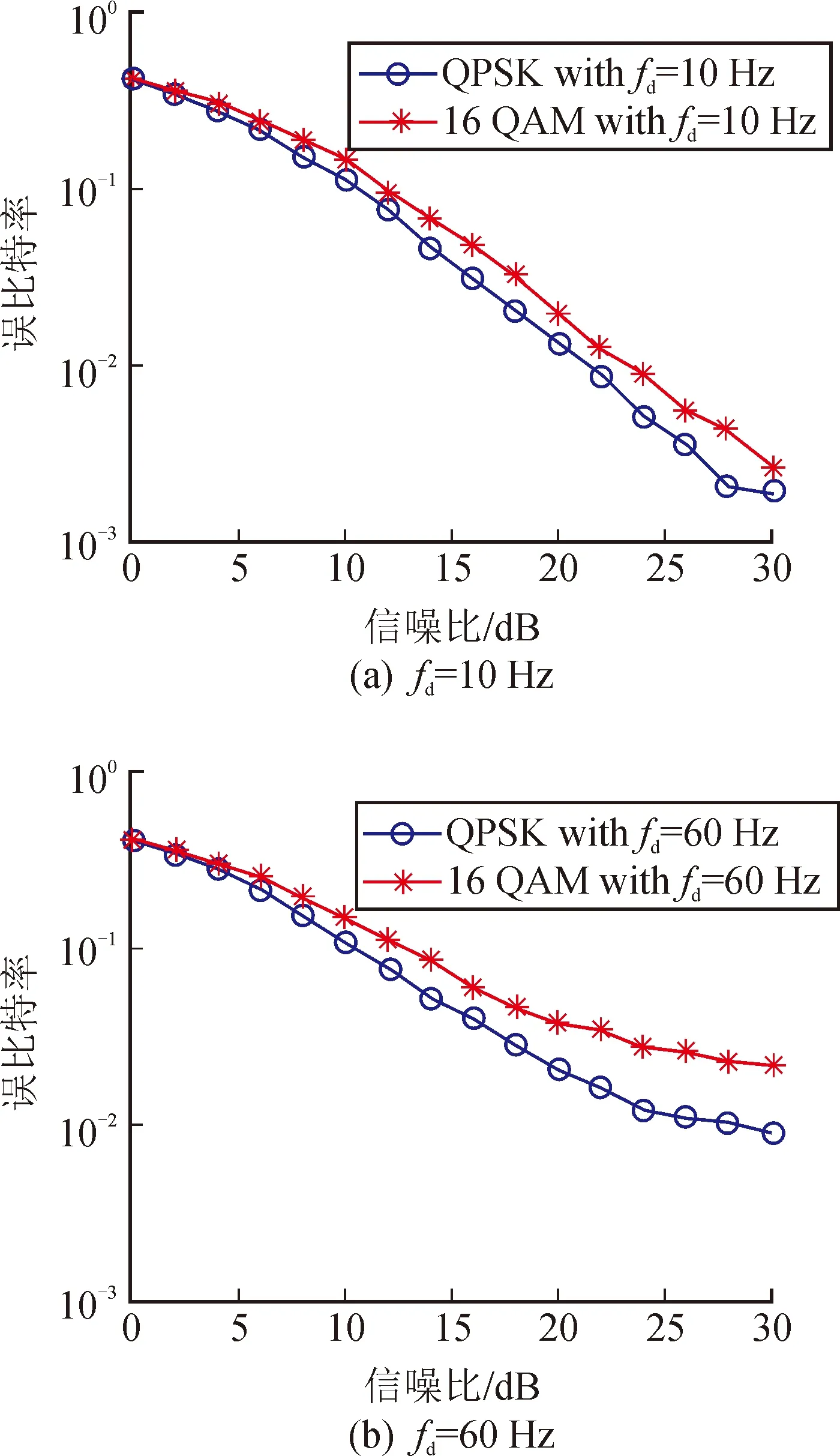
图6 OFDM均衡接收性能对比图

同时对比图6(a)、图6(b)中不同fd情况下系统BER性能可知,当fd大于60 Hz时,对应的BER性能已经出现10-2的误码平层,这主要是由于仿真2中提及的准静态过程所引起。由于fd变大,通信系统相应的准静态过程不断变小,而试验测试中的基本前提假设是6个OFDM符号对应时间内信道特性基本保证不变。因而,当fd增大时,使得系统信道出现较快的衰落波动,原始的信道估计必然不能实时准确地反映出通信系统真实的信道衰落情况,因而最终的频域均衡效果并不理想。

4 结论

文中通过对移动双弥散信道的模型构建,结合复等效处理、卷积及滤波等相关数字信号处理理论,提出了双弥散信道Matlab仿真的基本思路。该处理思路去除复杂的相关时间、相关带宽概念,建立了实际信道在Matlab仿真的对应技巧。仿真结果表明处理思路的正确性,能为通用的双弥散信道建模与仿真提供重要参考。下一步工作计划是对于信道的fd、多径数以及复杂的延时功率分布综合考虑,来更加定量化地分析双选信道,从而实现通信系统性能最优化。