基于滑动统计特征的信号非平稳度评价和比较

何浩祥， 张小福， 王小兵

(北京工业大学工程抗震与结构诊治北京市重点实验室 北京，100124)

引 言

大量实测数据及相关研究表明，从自然界及工程应用中获取的信号由于自身特性和噪声影响通常为随机信号。由于随机信号不能用确定性的时间函数描述，也不能被准确重现，因而必须采用统计方法进行研究。在不同领域，研究者需要根据各自需求获取能够表征时变随机信号的物理参数或统计特征并进行信号辨识或诊断，因此提取能够充分反映信号随机特性的统计量具有重要意义。

常用的随机信号统计量包括均值(一阶统计量)、方差和相关函数(二阶统计量)，此外还有三阶、四阶等高阶矩、高阶累积量以及高阶谱等高阶统计量。当统计量的变化与时间无关时，该信号被称为平稳信号。当统计量随时间改变时，该信号被称为非平稳信号[1-3]，工程中的随机信号往往是非平稳的。当平稳信号混入非平稳噪声时，可采用滤波或平滑技术将非平稳部分去除，还原信号的真实信息。当信号的非平稳性能够表征信号源的物理特性或本质特征时，需要对其时频变化特性进行研究并提取有效信息，为特征识别和频谱分析等提供技术支持。当信号的非平稳性能够反映信号短时或长期的变化规律时，需要关注其时变特征、局部畸变程度、趋势项及包络特征，为信号分类及故障诊断等提供依据。

虽然关于信号平稳性和非平稳性的定义相对明确，但实际评判过程较复杂，缺乏普遍适用的量化指标。有鉴于此，笔者对多种非平稳信号判定方法的优缺点进行比较，提出了基于滑动统计特征的信号非平稳性判定方法。该方法具有良好的识别能力，能够较细致地表征信号非平稳性。

1 非平稳度评价方法

针对如何判断指定信号是否具有非平稳性以及评价非平稳性的强弱即非平稳度，在不同研究领域存在不同的方法。例如，计量经济学中采用单位根检验方法[4-5]和平均熵理论[6]等；在非线性系统分析中常采用递归图进行判断[7-9]；在股票分析中采用Hurst指数[10]；对地震动信号分析采用穿零率[11]和非线性交叉预测法[12]。上述方法的优势和不足各不相同，实际应用中应根据工程需求和特点选择合适的方法。总体来讲，上述信号非平稳度的评定方法分为整体评价法和局部评价法。前者关注信号整体的非平稳性，只采用单一量值进行评定；后者能够适当反映信号局部或细节的非平稳程度，其数值是一组向量。为了根据信号特征需求选择合适的非平稳度评价方法，笔者对典型算法的适用范围和应用特点进行分析。

1.1 信号整体非平稳性评价方法

信号整体的非平稳性评价方法主要是根据相关指标判断信号非平稳性，并对其强弱进行简要评定。信号整体非平稳性的判定方法操作简便，可直观定性地反映信号的非平稳性。信号整体非平稳性评价方法主要包括自相关函数法、单位根检验、信息熵法及递归图法等。

自相关函数可刻画时间序列相邻变量之间的相关性，表达了同一过程不同时刻的相关程度。若某一时间序列信号的自相关函数随着延迟的增加迅速降为0，可认为该序列为平稳序列。如果自相关函数随着延迟的增加没有迅速下降为0，则可认为该序列是非平稳序列。自相关函数法简单易行且较为直观，但由于实际信号均是有限持时和有界的，随着延迟的增大，能够参与计算的数据维数不断减少，此时自相关函数已难以充分、准确地评估信号后期的平稳性。

单位根检验是指通过检验序列中是否存在单位根来判定序列的非平稳性[4]。序列中若存在单位根，信号即为非平稳的。单位根检验包括ADF(augmented Dickey-Fuller)检验、PP(Phillips-Perron)检验及NP(Ng-Perron)检验等。然而，单位根检验不能用于不同的非平稳随机过程的非平稳性的比较。

基于信息熵的非平稳度是通过提取原始信号中稳定信息结构中的信息熵的上确界，来判定信号的非平稳性[13]。一般情况下，相应的非平稳度量值界限不够明确，且不同非平稳信号的非平稳度量值差别很小，导致其应用和推广受到限制。

递归图分析是采用相空间重构原理显示系统递归特性的信号处理方法，主要通过相空间可视化的周期性轨迹来测定时序非平稳性[8]。递归图对状态空间中系统轨迹随时间的变化非常敏感，可对高维空间中的轨迹进行可视化、直观化的分析，但对部分非平稳性较强的长时信号的评价能力仍然有限。

1.2 信号局部非平稳性评价方法

虽然信号的整体非平稳性判定方法可以定性判定信号的非平稳性，但不能描述信号的时变特征，无法满足精度需求。有些随机信号从整体上看是平稳的，但在局部上表现出非平稳性和突变性。为了全面细致地判定信号的平稳性变化，需要同时观测信号的整体波动和局部突变，采用局部非平稳性评价方法对信号的统计量变化进行计算。典型的信号局部非平稳性评价方法主要包括非线性交叉预测法、基于希尔伯特-黄变换(Hilbert-Huang transform, 简称HHT)的平稳度法、穿零率以及Hurst图法等。

基于非线性交叉预测法将信号划分为若干相邻段，利用各分段之间的交叉预测误差表征各分段时序间的差异程度和平稳度。该方法的优点在于非平稳度时的计算不仅考虑了周期性波动，还考虑了时序趋势随时间变化情况，比较容易获得序列稳定的计算结果。由于对幅值较敏感且缺乏明确的判别阈值，该方法只能作为辅助方法。

穿零率表示单位时间内信号穿过零点的次数，可以用来反映信号的频率或周期随时间的变化特征，因而能够表现短时内的频率非平稳性。如果信号中高频部分突出，且与零线不完全相交，则很难通过穿零率鉴别出来，易发生高频遗漏现象。因此，用穿零率表示信号的非平稳性不够精准，一般需要和其他方法结合后进行综合判断。

Hurst指数是一种判断时间序列数据遵从随机游走还是有偏随机游走过程的指标，由重标极差分析方法计算得到[10,14]。另外，Hurst指数可以度量信号的趋势强度和噪声水平随时间的变化情况，可作为信号非平稳度的评定依据。首先，Hurst指数的计算按下式获得信号的累计离差xi,a

(1)

其中：ma为第a个区间内xu,a的平均值；xu,a为第a个区间内第t个元素的累计离差。

令极差Ra为累计离差xt,a的最大值与最小值之差。若以Sa表示第a个子区间l的样本标准差，可定义重标极差Ra/Sa，则所有A个重标极差的均值为

(2)

若子区间长度l是可变的，则

(R/S)l=KlH

(3)

其中：K为常数；H即为Hurst指数。

对式(3)两边取对数得到

log((R/S)l)=log(K)+Hlog(l)

(4)

可见，根据非线性时序的重标极差分析法得到的Hurst指数能有效地对时间序列做出预测，反映了数据的自相似程度及其二阶统计特征，可以用于对随机过程的非平稳性判定。

HHT从信号自身特征出发，用经验模态分解(empirical mode decomposition, 简称EMD)方法将信号分解成一系列的本征模态函数，对本征模态函数分量进行Hilbert变换，得到时-频域的能量分布，即Hilbert谱图H(ω,t)[15-17]。在此基础上，Huang提出了能量谱IE(t)和频域非平稳度Ds(t)的概念，用来反映信号在频域上的分布变化，具体计算过程如下。

对H(ω,t)进行时间t积分，得到Hilbert边际谱h(ω)，用来表示信号能量随频率ω的分布状态

(5)

计算平均边际谱n(ω)

(6)

频域非平稳度Ds(ω)为

(7)

类似于式(7)的定义，可以将平稳度定义为时间的函数。通过对H(ω,t)在频域积分得到Hilbert能量谱IE(t)，表示信号能量随时间的变化。

(8)

平均能量谱n(t)的计算方式为

(9)

信号的时域平稳度Ds(t)为

(10)

虽然HHT方法利用振幅-频率-时间三维分布可以直观反映信号的平稳性，但理论上还存在局限，尤其EMD分解没有明确的数学机理，信号分解稳定性和完备性的实现缺乏理论依据。因此，基于HHT的非平稳度分析需要进一步研究和深化。

对各种非平稳性评价方法的特性和不足进行整理和比较，如表1所示。可见，各种方法均有各自特点，同时也有很多局限和不足，需要改进。

表1非平稳性判定方法适用范围对比

Tab.1Comparisonoftheapplicablescopeofthemethodofnon-stabilitydetermination

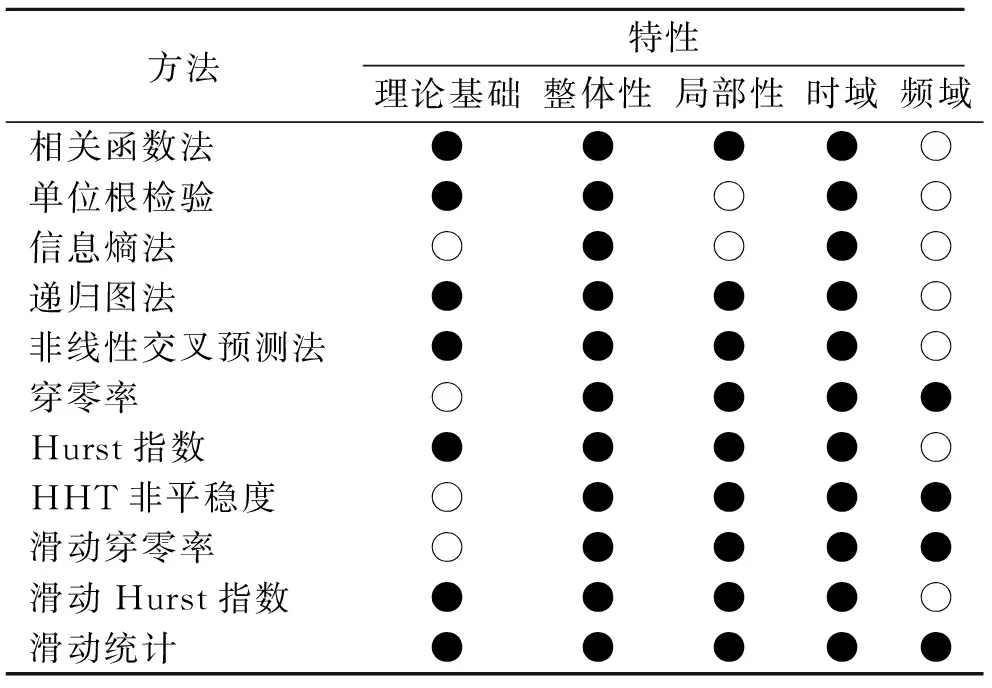
方法特性理论基础整体性局部性时域频域相关函数法●●●●○单位根检验●●○●○信息熵法○●○●○递归图法●●●●○非线性交叉预测法●●●●○穿零率○●●●●Hurst指数●●●●○HHT非平稳度○●●●●滑动穿零率○●●●●滑动Hurst指数●●●●○滑动统计●●●●●

●表示具备相应性能；○表示不具备相应性能

2 基于滑动统计特征的非平稳性评价方法

尽管各工程领域的实际信号表现出随机特性，但受产生机制和噪声特性影响，信号中的每个点都与附近的点相关。对大多数信号而言，一般都是邻近的信号对中心点的影响较大，距离较远的信号对中心点的影响较小，综合考虑信号点之间的关系和影响能力可以全面综合地评价随机信号的非平稳性。为了反映以上特性，通常采用加权滑动统计的方法对信号中的各点进行计算，即通过对指定范围内的信号点配以权重并采用相应范围内的统计值代替该点的方法实现数据平滑，以获取更为有效的信号特征。采用加权滑动统计方法对信号进行处理，相当于对信号进行了低通滤波，且相应的滤波器具有从通带到阻带平缓过渡的特点，因此可削弱瞬时随机波动对信号趋势的影响，反映局部变化特征并凸显整体规律。

笔者基于加权滑动统计方法提出了信号非平稳性评价方法。该方法根据信号分析的不同精度需求，对权重以及加权范围进行适当选取和调整，并以均值、方差和标准差、变异系数、穿零率及Hurst指数等作为滑动统计量，通过对上述统计量的分析和对比得到信号的波动和突变，对原始信号进行明确、定量的刻画，和对信号特征变化的发生时间和次序、严重程度及发展过程等细节进行描述，从而评定信号的局部和整体非平稳度。该方法简单实用，具有较好的适用性、敏感性和抗噪性。

2.1 滑动均值及滑动标准差

加权滑动均值是反映信号滑动变化规律的最基本统计量。对于信号的某点数据，将其及邻近的数据点做加权滑动平均，获得相应的加权滑动均值，即

(11)

其中：xi为信号中心点数值；m为xi时间轴两侧分别参与加权计算的点数；xj为需要考虑信号点数值；1-α为一阶权重；mi为i点处的滑动均值；k为在与xi距离长度为k点的权重阶数。

滑动标准差是对经过加权滑动法处理过的信号的标准差，反映了信号区间内考虑邻近信号影响的数据离散程度，公式为

(12)

其中：σi为i点处的滑动标准差，其他参数意义与式(11)中的相同。

信号本身受复杂因素以及内部互相联系的影响，对指数加权的思想是通过对较近的数据赋予较大的权重, 对较远的数据赋予较小的权重，保留了原始信号的真实性，能够有效反映信号的整体变化特征和局部突变大小。

2.2 滑动变异系数

变异系数是指标准差与其均值的比值，相当于按照其均值大小进行了标准化，与标准差一样反映信号的离散程度。当多个信号的度量单位或幅值不同时，采用滑动标准差表示不同信号的离散程度或非平稳性并不全面，而采用滑动变异系数可以进行更细致和客观的比较。笔者在滑动均值与滑动标准差的基础上提出了滑动变异系数的概念，用来表征信号局部离散特性和局部平稳性的变化，分析信号的变化趋势，确定信号的非平稳度。根据不同的工程需求，笔者提出了两种改进型滑动变异系数。

滑动变异系数μ为滑动方差与滑动均值的比值，即

μi=σi/mi

(13)

其中：mi为i点处滑动均值；σi为i点处滑动标准差。

在实际计算过程中，由于滑动均值往往出现零点或极小的数值，容易导致滑动变异系数的计算结果不收敛，从而无法直接用于判断随机过程的变化规律。因此，笔者对滑动变异系数的公式进行适当调整，提出了两种表达随机过程波动和突变的改进型滑动变异系数μ1和μ2，计算公式分别为

其中：a和b根据具体信号特点确定；a选取偏大的数值；b值选取的目的是使分母偏离零点，从而使变异系数收敛，因此宜选取较小的数值。

2.3 滑动Hurst指数

滑动Hurst指数是在传统Hurst指数计算方法的基础上，通过设定滑动维数m，将任一点i的有效滑动区间定为[i-m,i+m]，并计算区间内Hurst指数，最终得到整个时长的指数曲线。根据式(7)，滑动平均hurst指数的计算公式为

(i=m+1,,n-m)

(16)

滑动Hurst指数可以体现时变过程中某二阶统计量的变化，具有表达信号前后相似程度的能力，可直观描述信号变化过程中的非平稳性变化特性。

2.4 滑动穿零率

选取有效滑动区间[i-m,i+m]，通过计算该区间的穿零率得到i点处的滑动穿零率Pi。不断移动滑动区间的位置，得到不同滑动区间的穿零率。计算公式为

(17)

其中：i为矩形窗中心的位置；Pi为i点处的穿零率；Ni为滑动区间的穿零总数。

随着滑动区间的变化，滑动穿零率在一定程度上反映了不同时刻频率特性的变化规律，提取随机信号的时变特性，可用于判断信号的非平稳性变化。

3 不同信号非平稳性评价方法的对比

3.1 正弦叠加白噪声信号分析

选取正弦信号和白噪声信号的叠加信号进行非平稳性分析，以便反映各种评价方法的抗噪能力以及表征信号周期变化的能力。选取的正弦叠加白噪声信号的信噪比为30.24。对信号进行单位根检验，其单位根值为-1.11。检验结果表明，检验统计量值大于相应的DW临界值，从而接受H0，表明信号存在单位根，为非平稳随机过程。对正弦叠加白噪声信号非平稳性分析的结果如图1，2所示。

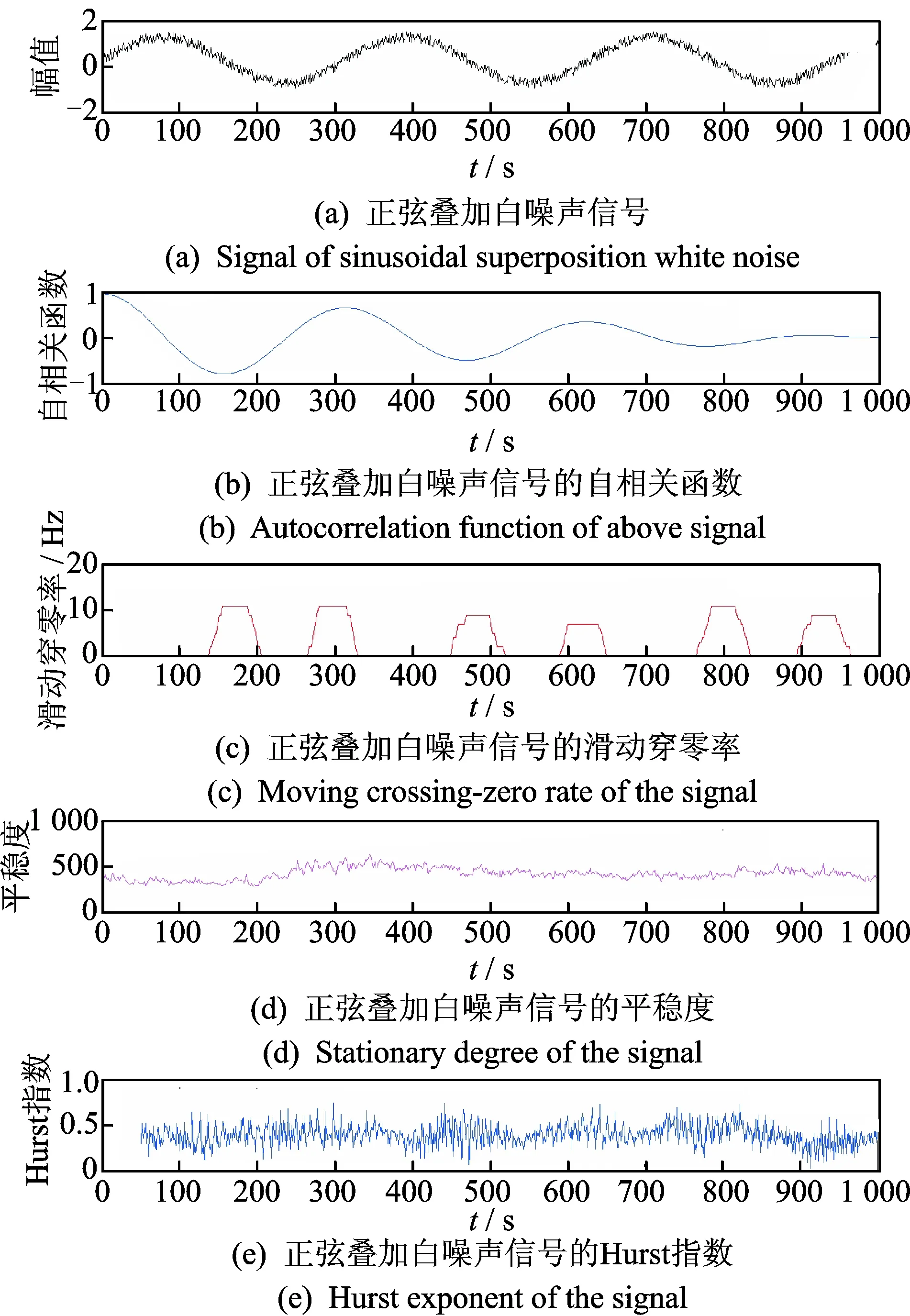
图1 基于典型算法的正弦叠加白噪声信号非平稳性分析Fig.1 Analysis of time invariant signal based on typical algorithms

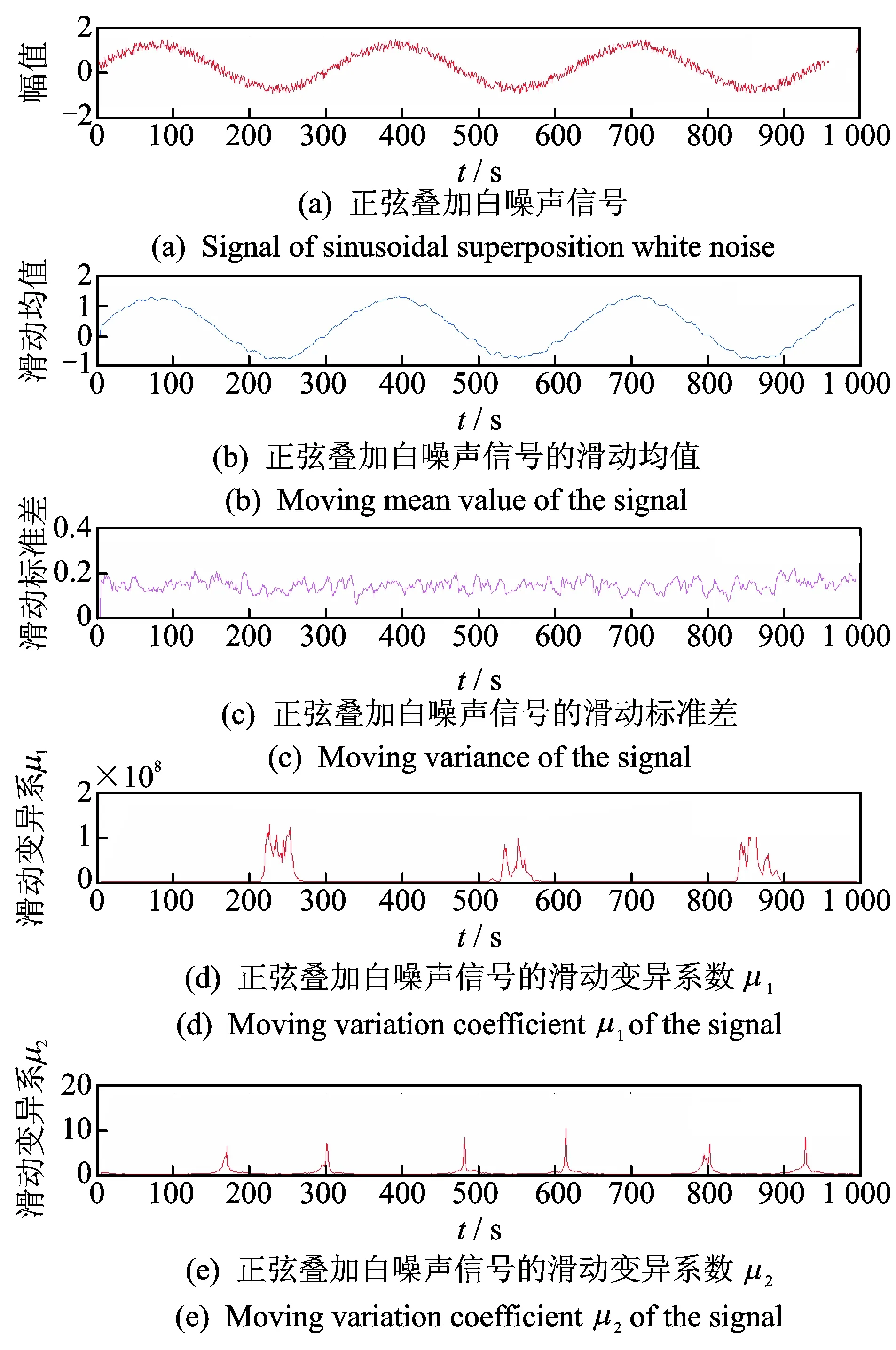
图2 基于滑动统计算法的正弦叠加白噪声信号非平稳性分析Fig.2 Analysis of time invariant signal based on movingalgorithms

图1中，自相关函数的数值衰减较缓慢且波动规律，表明信号具有平稳性和周期性。从滑动穿零率可以看出信号具有周期性，但高频噪声的变化特点没有得到表达。滑动Hurst指数和HHT平稳度的变化表明该信号是平稳的。图2中，滑动均值反映了信号的周期波动性，因滑动标准差变化较小，可判断信号是平稳的。每当原信号到达波谷时，滑动变异系数μ1发生较大的波动，从滑动变异系数μ1可以看出信号具有周期性。原始正弦信号变动速度最大的位置与滑动变异系数μ2突变的位置相同，但由于白噪声影响的随机性，突变大小不尽相同，信号的抗噪性在滑动变异系数μ2中凸显出来。由此可见，滑动变异系数具有准确表达周期性变化和突变的能力。

3.2 机械故障信号分析

机械设备振动信号的频率成分较丰富，具有典型的非平稳性和非线性，且各种激励间存在干涉、耦合和瞬态响应等影响，传统方法不能正确定位故障。为了及时、准确地对机械设备的各种异常状态或故障状态做出诊断、预防或消除，需要对设备振动信号进行分析。笔者选取美国西储大学轴承数据中心网站公开发布的轴承探伤测试数据集中的典型信号，振动信号由3组不同的机械故障损伤信号组合而成，每组信号的长度为1 000个数据点。

对选取的机械故障信号进行单位根检验，3段故障信号及其组合的单位根值分别为-7.48，-7.64，-11.7和-14.1。都在1%的显著水平下拒绝原假设，即4组信号都不存在单位根，为平稳随机过程。这些信号从表观上看具有较明显的非平稳性，可见，用单位根检验方法进行信号局部平稳性分析易出现误判，需要联合其他方法使用。

利用其他典型的非平稳性算法分析信号的非平稳性结果如图3，4所示。典型算法对机械故障类型均有一定的区分能力。HHT平稳度可以明显区分不同类型的信号特征，滑动Hurst指数也具有良好的效果。滑动均值和滑动标准差的结果使得原始信号的非平稳变化特征被凸显，其中滑动变异系数μ2刻画信号局部非平稳性的能力更强。

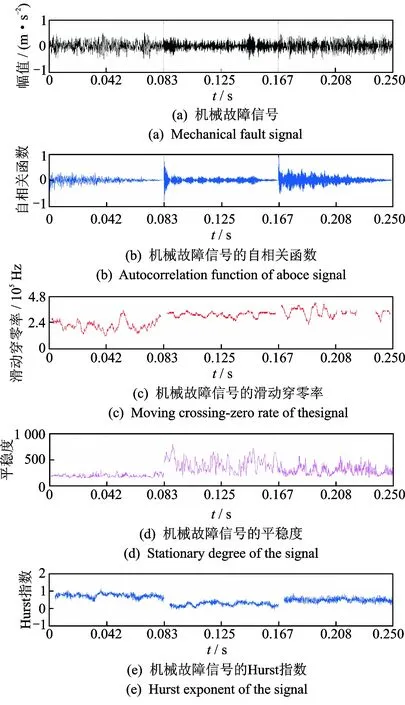
图3 基于典型算法的机械故障信号非平稳性分析Fig.3 Analysis of mechanical signal based on typical algorithms

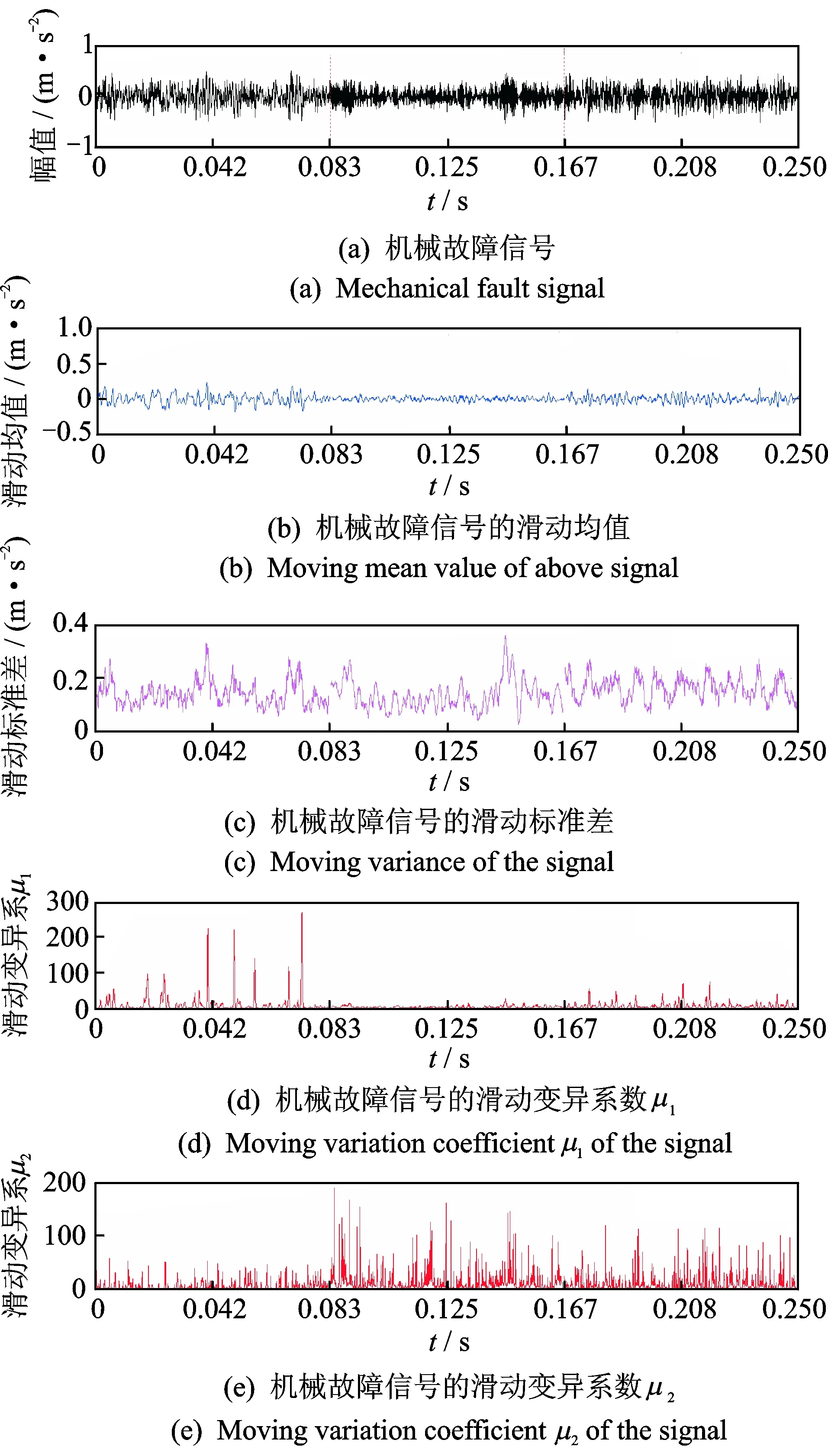
图4 基于滑动统计算法的机械故障信号非平稳性分析Fig.4 Analysis of mechanical signal based on moving algorithms

3.3 心电图信号分析

心脏病是威胁人类健康的最严重疾病之一，其诊断分析依据主要是通过记录心电信号的心电图(electrocardiogram, 简称ECG)。心率变异性就是指主次心跳期间的时间差异，可用来预测心脏性猝死、评价心脏自主神经的均衡性以及相关的病理状态。笔者选取MIT-BIH心律失常数据库中3段具有不同病状心脏病病人的ECG信号，组成一组信号，每段心脏病状的信号长度为2 048个数据点。可以看出，组合信号中3段不同病变的信号没有明显的视觉差异，心率的变异性和病症结果很难用肉眼进行直观判断。对选取的ECG信号进行单位根检验，结果表明3段故障信号及其组合的单位根值分别为-13.46，-10.57，-6.96和-16.0，都在1%的显著水平下拒绝原假设，所以认为4组信号都不存在单位根，为平稳随机过程，仍然出现了误判。

为了在实际过程中准确诊断心脏变异的时刻并区分不同的症状，利用多种信号非平稳性评定方法对ECG组合信号的非平稳性进行分析，如图5和图6所示。可以看出，不同评定方法的区分能力具有显著差异。与机械故障信号的区分能力相比， HHT平稳度和滑动Hurst指数不易区分不同组信号，但滑动穿零率有相对较好的区分能力，能判断出心脏信号的变异时刻。滑动均值和滑动标准差使原始信号变化特征被凸显。滑动变异系数的表现能力最出众，滑动变异系数μ1能够区分不同变异状态以便得到变化的时刻，而滑动变异系数μ2可以得到心率变异性以及心脏突变的时间点和大小，有助于专业人员对心律不齐、心肌炎等病状的诊断。

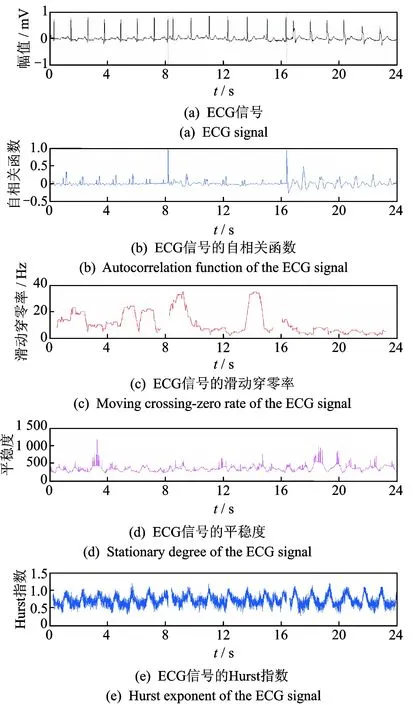
图5 基于典型算法的ECG信号非平稳性分析Fig.5 Analysis of ECG signal based on typical algorithms

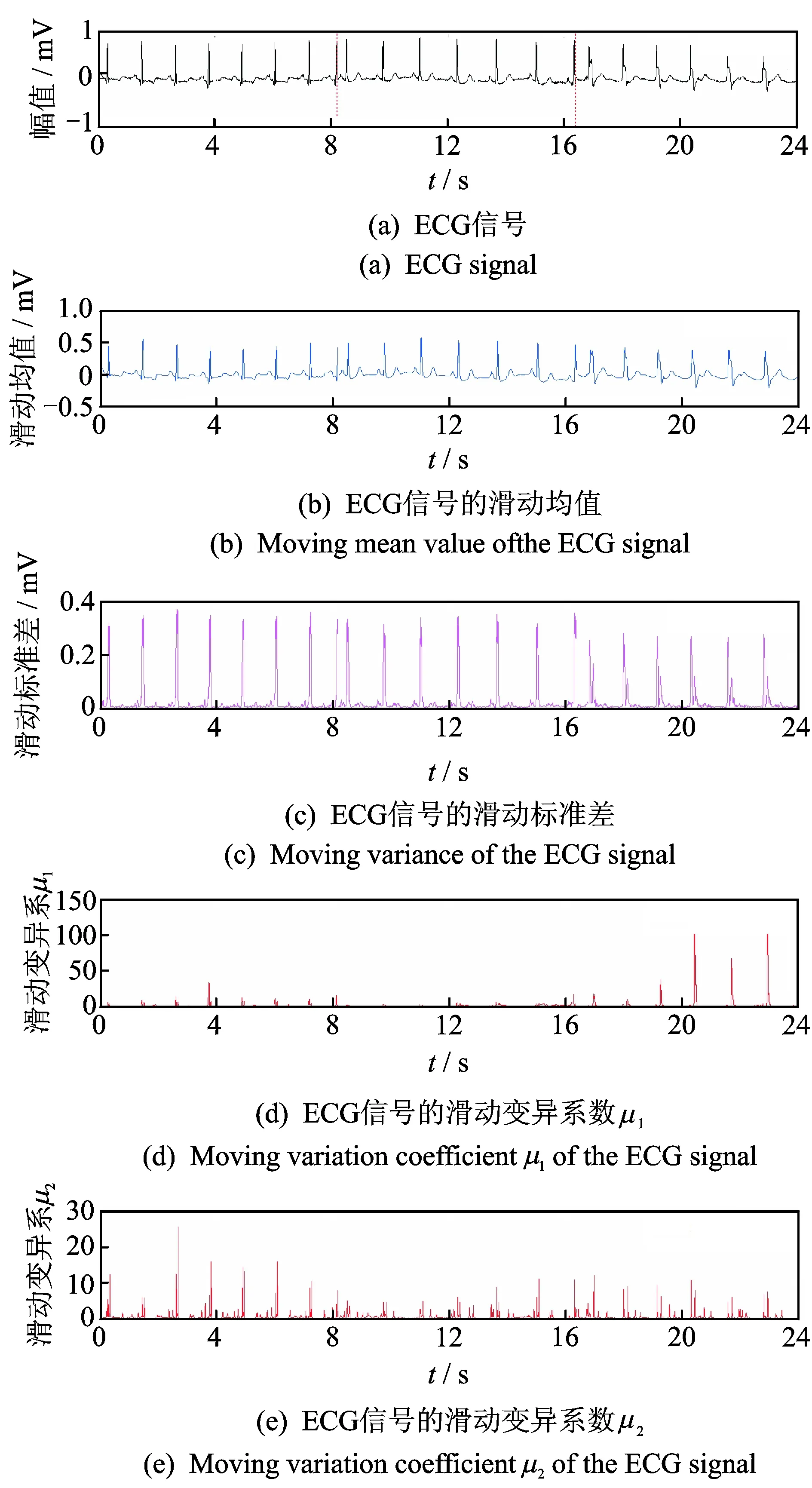
图6 基于滑动统计算法的ECG信号非平稳性分析Fig.6 Analysis of ECG signal based on moving statistic algorithm

3.4 基于不同平稳度的信号识别能力比较

上述实例分析主要从表观差异性比较不同平稳度分析方法反映信号非平稳特征的能力，在实际应用中往往需要针对工程需求实现信号分类或故障诊断的自动化、实时化和智能化，因此通常需要利用模式识别方法快速准确地根据信号特征进行分类和识别。如果采用平稳度方法，需要选择性能优异的模式参数并建立有效的特征向量，可选择区分能力较强的滑动穿零率、HHT时域平稳度、滑动Hurst指数、滑动变异系数μ1和μ2作为模式参数。由于信号能量即信号幅值平方之和是信号的基本特征且物理意义明确，笔者对机械故障信号和EGG信号的不同部分进行模式参数计算并获得相应的信号总能量。为了消除不同参数的量纲效应，对每种参数的信号总能量分别进行归一化处理，如图7和图8所示，并进行区分能力对比。

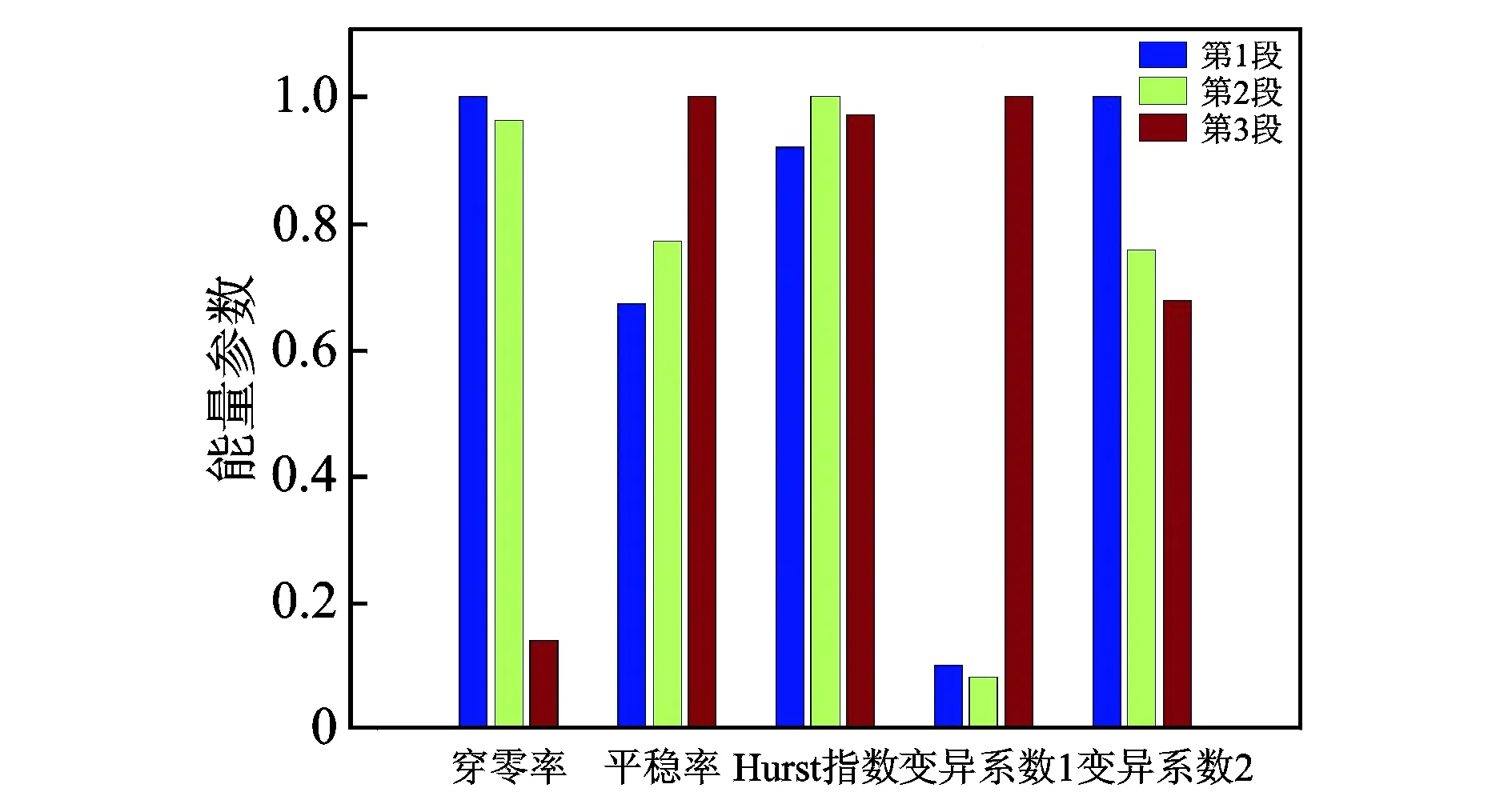
图7 机械故障信号非平稳性能量参数Fig.7 Nonstationarity index of mechanical fault signal

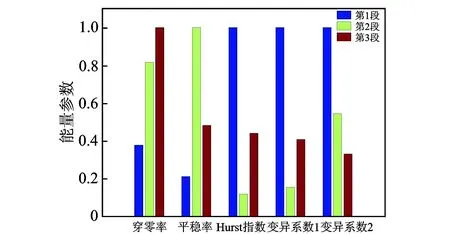
图8 ECG信号非平稳性能量参数Fig.8 Nonstationarity index of ECG signal

结果表明：在机械故障信号的分析中，HHT平稳度、滑动Hurst指数和滑动变异系数的信号能量均有较好的区分能力，但滑动穿零率略差；在ECG信号的分析中，仅有HHT平稳度和滑动变异系数μ2的信号能量具有良好的区分能力。因此，对于不同类型的信号，HHT平稳度和滑动变异系数μ2的信号能量区分度较大，利于实现模式识别。此外，由于滑动变异系数μ2的表观区分度也较好，故将其作为信号平稳度分析的重要指标，并在故障诊断和模式识别中加以应用和推广。

4 结束语

非平稳信号的统计特征具有时变性，准确而全面地提取其必要的统计信息并实现非平稳性评价可为信号诊断提供有效工具。现有的非平稳性评价方法均有各自的特点和局限性。笔者根据滑动统计分析的思想提出滑动变异系数和滑动Hurst指数等概念和计算方法，力求充分表征信号的时变细节和不同信号的差异，从而为非平稳度分析提供有效的支持。通过对不同领域信号的计算、区分和诊断，并与其他典型非平稳性评价方法进行比较，结果表明，滑动变异系数可以准确可靠地反映信号的波动和变异情况，对非平稳信号的平稳性具有良好的辨识能力，基于滑动统计特征的信号非平稳度计算方法具有较强的实际应用前景。