基于过桥车辆响应的遗传算法桥梁损伤识别

毛云霄， 王英杰, 2， 肖军华， 时 瑾, 2

(1.北京交通大学土木建筑工程学院 北京，100044) (2.北京交通大学轨道工程北京市重点实验室 北京，100044) (3.同济大学道路与交通工程教育部重点实验室 上海，201804)

引 言

车辆运行速度、轴重的不断提高，加速了对桥梁结构的冲击破坏，如何对其进行健康监测并开展损伤识别已成为当前极具现实意义的研究课题之一[1]。当车辆在桥梁上运行时，由于受到车辆荷载的作用桥梁将产生振动并发生变形，而桥梁的振动变形又会回馈到车辆上，从而引起运行中车辆的振动变形。因此，在车辆过桥引起的车桥耦合振动问题中，桥梁和车辆的动力响应都包含桥梁结构模态或几何参数信息，可以单独采用桥梁响应或车辆响应对桥梁损伤进行识别。

在利用桥梁响应进行损伤识别方面已有大量研究成果。He等[2]建立了车桥耦合振动有限元模型，利用遗传算法调用桥梁动力响应，通过匹配最佳损伤模式对桥梁损伤进行了识别。单德山等[3]采用模式识别的聚类分析法将实测桥梁响应与预设损伤模式进行对比，有效估计了桥梁结构的损伤位置和损伤程度。刘宇飞等[4]采用缺口平滑拟合技术，利用移动荷载引起的结构动力响应分析了桥梁结构的平均曲率模态，对桥梁结构局部损伤进行了定位。赵俊等[5]研究了移动荷载作用下简支梁动态响应特征，并基于小波分析多变率方法利用梁上某点振动信号识别了单个或多个裂纹损伤的位置。以上研究采用桥梁响应数据成功识别了桥梁损伤位置及损伤程度，然而在实际应用中由于测试条件的限制，不可能对所有桥梁开展动力响应测试以获得响应数据。随后，不少学者开展了利用过桥车辆响应识别桥梁损伤的研究。Li等[6]从车辆响应中提取桥梁频率对损伤位置进行初步识别，利用GA算法进行二次识别。战家旺等[7]构建了列车动力响应对桥梁刚度下降率的灵敏度方程，利用约束优化方法求解实现了桥梁损伤诊断。王树栋等[8]利用实测过桥车辆动力响应，以桥梁单元刚度损伤为识别因子，结合最小二乘法和正则化方法识别了桥梁损伤。以上研究均从车辆动力响应入手，运用不同方法实现了桥梁损伤的识别，取得了大量研究结论。

笔者在考虑线路不平顺的基础上将简支梁划分为有限单元，建立了移动车辆过桥耦合系统模型。通过车辆动力响应的有限元计算数据和模拟实测数据构建目标函数，以损伤位置和损伤程度作为识别因子，利用GA算法实现桥梁不同损伤状态的识别。针对单目标和多目标桥梁损伤识别工况，运用统计方法开展多次独立重复计算，采用成功率及首次出现最优解平均迭代代数分析了GA算法对桥梁损伤状态的识别效率。

1 移动车辆过桥模型

如图1所示，本研究主要研究采用车体加速度响应来识别桥梁结构损伤的可行性，因此在建立移动车辆过桥模型时，采用如下假设[9-10]：a. 采用多刚体动力学理论建立车辆模型，其中车体、转向架和轮对模拟为刚体，一系和二系悬挂系统按线性弹簧、阻尼考虑；b. 为便于桥梁损伤位置和程度的识别，采用有限元法模拟简支梁变形，且桥梁损伤仅考虑抗弯刚度的降低；c. 忽略轨道结构对车桥系统振动的影响，且采用轮轨密贴接触假定，不考虑轮轨分离对车桥系统动力响应的影响；d. 线路不平顺采用我国铁路实测数据，以充分考虑其对车桥系统动力响应的影响；e. 初始时刻第1轮对位于桥梁左端，且假定车辆以恒定速度v匀速通过桥梁。

图1 移动车辆过桥模型Fig.1 Vehicle/bridge system model

1.1 车辆模型

如图1所示，车辆模型只需考虑6个自由度，即车体、前后转向架的沉浮运动Zv,Zt1,Zt2和车体、前后转向架的点头运动θv,θt1,θt2。根据达朗贝尔原理建立车辆运动方程。

车体的沉浮和点头运动方程为

(1)

(2)

其中：mv，Iv分别为车体的质量和点头转动惯量；ks，cs分别为二系悬挂的刚度和阻尼；lt为车辆定距之半。

前后转向架的沉浮和点头运动方程为

(3)

(4)

其中：mt，It分别为前后转向架的质量和点头转动惯量；lw为前后转向架固定轴距之半；s=1-4代表第s位轮对；j=1-2代表前后转向架。

Ftj为转向架作用在车体上的力

(5)

Fws为第s位轮对作用在转向架上的力

(6)

其中：s=1-2时，j=1；s=3-4时，j=2；Zb(xws,t)为第s位轮对所对应的桥梁位移；r(xws)为第s位轮对所对应的线路不平顺。

1.2 桥梁模型

简支梁跨度为L，抗弯模量为EI，单位长度质量为m。为考虑简支梁损伤对车桥系统动力响应的影响，采用有限单元法建立桥梁模型，将简支梁划分为长度为l的Nb个有限单元，如图2所示。

图2 梁单元及荷载Fig.2 Degree of freedom of beam element and applied loads

假设t时刻第s位轮对位于第i个梁单元上，且其距离其所在单元左端的相对距离为ξws，此时该轮所在位置处简支梁的竖向位移[11]可表示为

yi(ξws,t)=Niqi

(7)

其中：qi为节点位移向量，即qi=[ui,θi,ui+1,θi+1]；Ni为梁单元的形函数，采用Hermitian三次插值函数，即

(8)

梁单元的质量和刚度矩阵分别为

(9)

(10)

如图2所示，fs为作用在第i个梁单元上的外荷载，包括车体、转向架和轮对的重力、轮对的惯性力以及悬挂系统产生的弹性力和阻尼力[9, 12]，即

(11)

通过组装简支梁单元刚度、质量矩阵及计算等效节点荷载，得到简支梁的运动方程为

(12)

其中：MB，KB，CB分别为简支梁的质量、刚度和阻尼矩阵；阻尼矩阵采用Rayleigh阻尼表示。

qB为简支梁各单元节点向量，即

qB=u1,θ1，，ui,θi，u2Nb+1,θ2Nb+12Nb+1×1

(13)

FB为等效节点向量，即

(14)

将式(8)，(11)代入式(12)，将等式右边的未知加速度、速度和位移项移动到左边；将式(5)，(6)代入式(3)和式(4)，将等式左边的线路不平顺项移动到右边，同时与式(1)，(2)联立，得到移动车辆过桥的运动方程，其矩阵表达式为

(15)

对于移动车辆过桥系统，在任一时刻需要重新组装式(15)的质量、刚度和阻尼矩阵，且计算外荷载向量都在发生变化。根据车桥耦合系统的时变特性，笔者采用Newmark-β数值积分法求解每一时刻车桥系统的动力响应。

2 遗传算法识别

遗传算法是建立在自然选择和种群遗传基础上的迭代进化，具有广泛适用性的随机性优化搜索方法[13]。笔者基于过桥车辆动力响应的遗传算法桥梁损伤识别主要包括两部分：a. 利用车桥耦合系统有限元模型计算车辆动力响应；b. 利用遗传算法对桥梁损伤位置和程度进行识别。如图1所示，将简支梁划分为Nb个有限单元用于损伤定位，各损伤位置采用GA编码方式进行编码；单元损伤程度仅仅考虑刚度损伤，假定有Nd组损伤程度需要识别，同理对损伤位置进行编码。本遗传算法的目标函数(objective function，简称OBJ)定义为有限元计算响应与实测响应之间的方差平方均值

(16)

其中：f(i)为实测数据；f*(i)为有限元计算数据；i和t分别为每一离散时刻车辆从桥梁左端到桥梁右端的总时间。

本研究中，实测数据采用模拟实测数据，假定桥梁存在某一特定损伤时，利用车桥有限元模型计算该状态下车辆动力响应，并在此基础上添加一段实测噪声作为模拟实测车辆动力响应f(i)。有限元分析数据f*(i)同样利用车桥有限元模型计算得到车辆动力响应，不同之处在于此时的桥梁损伤状态是通过GA算法在搜索空间内随机产生的。

将式(16)作为遗传算法识别桥梁损伤的目标函数，以此为依据计算适应度函数。分析可知，当GA识别的损伤状态与预设实际损伤状态吻合时，式(16)的目标函数值最小，此时对应的适应度函数值最大。本研究遗传算法搜索过程属于最小化优化问题，即为寻找目标函数的最小值，即目标函数越小，个体适应度值越大。

笔者以车辆过桥动力响应作为输入数据，采用遗传算法对不同桥梁损伤状态进行识别，识别流程如图3所示。

1) 预设某种桥梁损伤状态，利用车桥模型计算该状态下车辆响应，并考虑噪声影响形成模拟实测数据f(i)。

2) 利用GA算法在可能损伤位置(1～Nb)、可能损伤程度(0～Nd)解空间中产生n个初始种群(父辈)，每一个初始种群代表一种损伤状态，对其进行格雷编码。

3) 对第2步产生的n个父辈个体，计算父辈所对应损伤状态下车辆过桥动力响应f*(i)，与第1步模拟实测数据f(i)对比，按照式(16)计算父辈目标函数OBJ，得到父辈适应度函数。

4) 根据适应度函数值对父辈编码进行选择、交叉、变异和重组。

5) 生成第i代子代，子代中每个个体对应新的损伤状态。

6) 计算第i代子代个体所对应损伤状态下车辆过桥动力响应分析数据f*(i)，同理与模拟实测数据f(i)对比得到子代目标函数及其适应度函数。

7) 当子代代数i小于最大遗传代数Maxgen时，该子代成为新一代父辈重复步骤4～6，直到子代代数i达到最大遗传代数，结束识别。输出最大遗传代数Maxgen内每一代最优识别状态并计算其目标函数，找出所有代中最小目标函数对应状态，即为GA识别结果。

图3 遗传算法流程图Fig.3 Flow-chart of GA method

在采用遗传算法对桥梁损伤进行识别过程中，计算结果具有一定的随机性、跳跃性[14]。这可能是在某一代计算过程中已经找到最优解，但由于尚未达到最大遗传代数Maxgen，后续计算中可能跳出最优解找到次优解，经历几代后又再次跳回最优解，所以在特定最大遗传代数Maxgen内可能多次找到最优解，也可能一直没有找到最优解。同时，遗传算法在求解进化问题过程中虽然存在一定随机性，但又具有一定稳定性，可通过多次重复计算对结果进行统计分析[15]。因此，笔者对各工况下桥梁损伤识别过程进行多次独立重复计算，统计多次计算中成功找到最优解的次数及每次计算中首次出现最优解迭代代数，采用识别成功率和首次出现最优解平均迭代代数来表示GA算法识别效率。为方便表述，采用识别效率参数EP1表示识别成功率，即多次独立重复计算中成功找到最优解的次数占计算总次数的比值；采用识别效率参数EP2表示首次出现最优解平均迭代代数，即多次成功损伤识别中首次出现最优解的平均迭代代数。

3 数值算例

线路不平顺是影响车辆动力响应的主要因素之一[16]，也是车桥耦合振动系统的激励源，本研究采用一段我国铁路实测线路不平顺样本，如图4所示。

图4 线路不平顺Fig.4 Track irregularity

笔者考虑3跨简支梁连续布置，采用一节车辆完全通过中间跨简支梁全过程中车体质心处的垂向加速度数据识别桥梁损伤，即第1位轮对上桥至第4位轮对下桥。先计算得到桥梁不同损伤工况下的车体加速度响应，以此作为输入数据并与GA识别方法相结合，实现简支桥梁损伤识别[17]。如图1所示，假设车辆以15m/s的速度通过简支梁，计算采用的桥梁、车辆参数[18]及GA算子参数[19]如表1所示。

3.1 单目标识别

在单目标识别中假设只有一个单元发生损伤，且仅仅识别损伤单元的位置或程度。首先分析损伤单元位置的识别。假设损伤单元位置未知，而损伤单元程度已知，均为30%。如表2所示的工况1～3，单个损伤单元位置分别假设为1，63，96，代表桥梁端部、跨中及3/4跨位置，以判断GA算法对桥梁损伤单元位置的识别效率。由表1可知，此时Nb=128，识别目标将从128个可能位置中寻找。在损伤单元位置识别中选取初始种群数量为4，最大遗传代数Maxgen为50，每种工况独立重复计算300次。对300次识别中GA识别效率参数EP1和EP2进行统计，如表2所示。

由表2可知，对于单个损伤单元位置识别，3种计算工况都能成功识别出损伤单元位置。针对不同位置的识别，识别成功率(EP1)均在90.00%以上，说明GA算法对损伤单元位置的识别效率显著。统计得到首次出现最优解平均迭代代数(EP2)均在20代以内，说明GA算法在平均迭代20代内即可找到单个损伤单元位置，这为设定最大遗传代数Maxgen提供了一定依据。

表1车桥模型及GA算子参数

Tab.1Parametersofvehicle/bridgesystemandGAoperators

类别参数数值桥梁跨度L/ m32弹性模量E/(N·m-2)3.45×1010惯性矩I/ m411.1 单位长度质量m/(kg·m-1)22 425梁单元长度l/ m0.25 有限单元个数Nb128车辆车体的质量mv/ kg38 884 车体点头转动惯量Iv/(kg·m2)1.91×106转向架质量mt/ kg3 060 转向架点头转动惯It/(kg·m2)3.2×103轮对质量mw/ kg1 517一系悬挂刚度kp/(N·m-1)1.772×106 二系悬挂刚度ks/(N·m-1)4.5×105一系悬挂阻尼cp/(N·s·m-1)2×104二系悬挂阻尼cs/(N·s·m-1)2×104车辆定距之半lt/m8.75转向架固定轴距之半lw/m1.25损伤参数损伤位置编码方式7位格雷码损伤程度步长δ/%10损伤程度区间[a , b]a=0%, b=70%损伤程度编码方式3位格雷码GA算子初始种群数量n视不同计算工况而定选择方式轮盘赌选择交叉方式两点交叉交叉率0.6变异方式离散变异变异率0.1Maxgen视不同计算工况而定

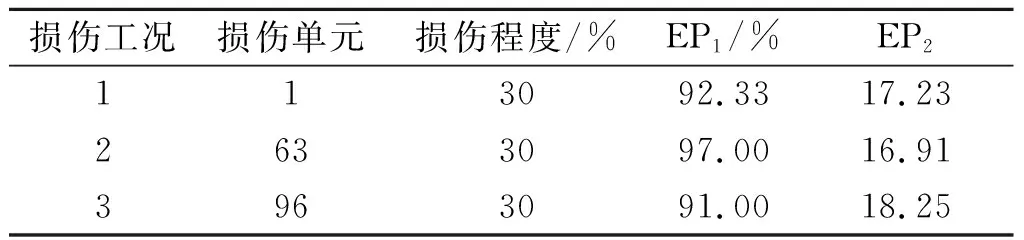
表2 单目标识别(损伤单元位置)

针对工况1～3，统计上述300次独立重复计算中识别位置的变化如图5所示。可以看出，工况2和工况3的识别结果有小部分浮动，但基本在目标损伤单元63和96附近浮动，即识别结果与既定损伤工况基本一致；而工况1的识别结果绝大部分定位在目标损伤单元1，少量识别结果跳跃到了损伤单元128。可见，GA算法对跨中及3/4跨处的损伤识别效果较桥梁端部损伤更为稳定，这可能由以下两点原因造成：a. 与桥梁中部发生损伤相比，桥梁端部发生损伤对车辆加速度响应影响较小；b. 由于简支桥梁的对称性，其左端或右端发生损伤时，车辆过桥响应同样存在对称性所致。

图5 损伤位置识别结果Fig.5 Results of damage location detection

同理，分析单目标识别中损伤单元程度的识别，假设损伤单元程度未知，而损伤单元位置已知。如表3所示的工况4～6，损伤单元1，63和96分别对应的损伤程度为30%，70%和50%，以判断GA算法对桥梁损伤单元程度的识别效率。由表1可知，此时Nd=8，识别目标将从8个可能程度中寻找损伤程度。选取初始种群数量为4，最大遗传代数Maxgen为50，每种工况独立重复计算300次。对计算结果进行统计分析得到识别成功率EP1及首次出现最优解平均迭代代数EP2，如表3所示。

表3 单目标识别(损伤单元程度)

由表3可知，对于单个损伤单元程度识别，3种计算工况都能成功识别出损伤单元程度；针对不同程度的识别成功率(EP1)均在99.00%以上，且能在5代以内首次找到最优解。与单个损伤单元位置的识别相比，GA算法对损伤单元程度的识别效率更为显著。这是由于对损伤单元位置进行识别时，其GA搜索空间大小由损伤位置的128减少到损伤程度的8，因此能很快找到最优解。

针对工况4～6，统计上述300次独立重复计算中识别程度的变化如图6所示。可以看出，针对工况4和工况6，300次的识别结果都与既定损伤工况一致，工况5在300次识别中仅出现两次错误识别，进一步说明了GA算法识别效率与搜索空间大小关系密切。

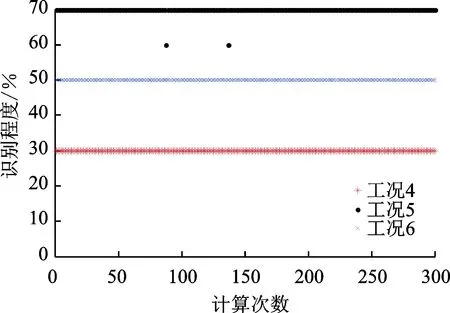
图6 损伤程度识别结果Fig.6 Results of damage degree detection

3.2 多目标识别

在多目标识别过程中假定损伤单元位置、损伤单元程度和损伤单元数目均未知，此时搜索空间将迅速扩大，例如有m个单元发生损伤，则搜索空间基数从单目标识别的8或128变为(8×128)m。此时为了识别桥梁损伤状态，若每次直接采用排列组合并利用有限元模型计算响应数据，再而搜索解空间，将耗时耗力，而GA算法可实现多点寻优，显著减小有限元模型计算量。

为观察多目标识别过程中目标函数的变化，以63单元刚度损伤30%为例，在识别过程中损伤单元位置和程度分别存在128和8种可能，GA算法搜索空间域大小为(8×128)1=1 024。针对1 024个备选可能，计算其目标函数并取对数绘图，如图7所示。可以看到明显的峰值点，该点所对应的损伤单元位置为63，损伤单元程度为30%，即为GA算法搜索目标函数最小值所对应的点。

图7 目标函数对数值Fig.7 Logarithm value of OBJ

多目标识别过程中，最大遗传代数Maxgen仍取50，但由于搜索空间域明显增大，初始种群数量取4可能无法同时满足计算效率及识别效率的要求。为此，同样以63单元刚度损伤30%为例，将初始种群数量由4变化到64，步长取4，研究初始种群数量对识别效率的影响，如图8所示。

图8 初始种群数量对识别效率的影响Fig.8 Effect of initial population number to detection efficiency

从图8可以看出，当初始种群数量由4增加到12时，识别成功率(EP1)明显提高，由46.33%提高到94.33%。此后，随着初始种群数量的增加，识别成功率(EP1)缓慢增加，直到取24时达到100.00%，此后一直保持100.00%。另外，首次出现最优解平均迭代代数(EP2)随初始种群数量增加整体呈下降趋势。由此可见，桥梁损伤识别成功率(EP1)和首次出现最优解平均迭代代数(EP2)受初始种群数量影响较大。图8中交点位置对应的初始种群数量为8，识别成功率(EP1)约为85%，首次出现最优解平均迭代代数(EP2)约为22。综合考虑损伤识别成功率(EP1)达到90%以上，首次出现最优解平均迭代代数(EP2)小于最大遗传代数一半，故多目标识别GA算法选取初始种群数量取16。

在以下算例中选定初始种群数量为16，首先分析仅有一个单元发生损伤(即损伤单元位置和损伤程度均未知)的情况，设定工况7，8，9和10，具体损伤单元位置及损伤单元程度如表4所示。

表4 多目标识别(损伤单元位置+损伤单元程度)

采用前文所述车桥系统参数及GA算子参数对工况7～10进行计算，识别结果如表4所示。由表4可知，对于多目标损伤识别，4种计算工况都能同时成功识别损伤位置和程度。从计算结果来看，工况7识别成功率(EP1)明显小于工况8，9和10，这是由于GA算法对桥梁端部损伤识别效率不及桥梁跨中及3/4跨，与单目标损伤识别中位置识别类似。4种工况首次出现最优解平均迭代代数(EP2)在20代内，这也与单目标损伤识别中位置识别结果一致，主要是由于GA算法对损伤程度识别效率较高(见表3结果)，在对某单元损伤位置和程度同时识别时并不因增加程度识别而降低识别效率。对比工况8和工况10可以看出，不同损伤程度对多目标损伤识别效率影响不大。

针对工况7～10，同样统计上述300次独立重复计算中识别结果的变化如图9所示。可以看出，工况8，9和10识别结果基本在目标损伤位置和损伤程度附近浮动，与既定损伤工况基本一致；而工况7的识别结果绝大部分定位在目标值(损伤单元1、损伤程度30%)，部分识别结果的损伤单元或损伤程度附近发生了漂移，相比其他3种工况识别结果稳定性较差。这进一步说明了该算法对端部损伤识别成功效率较低。

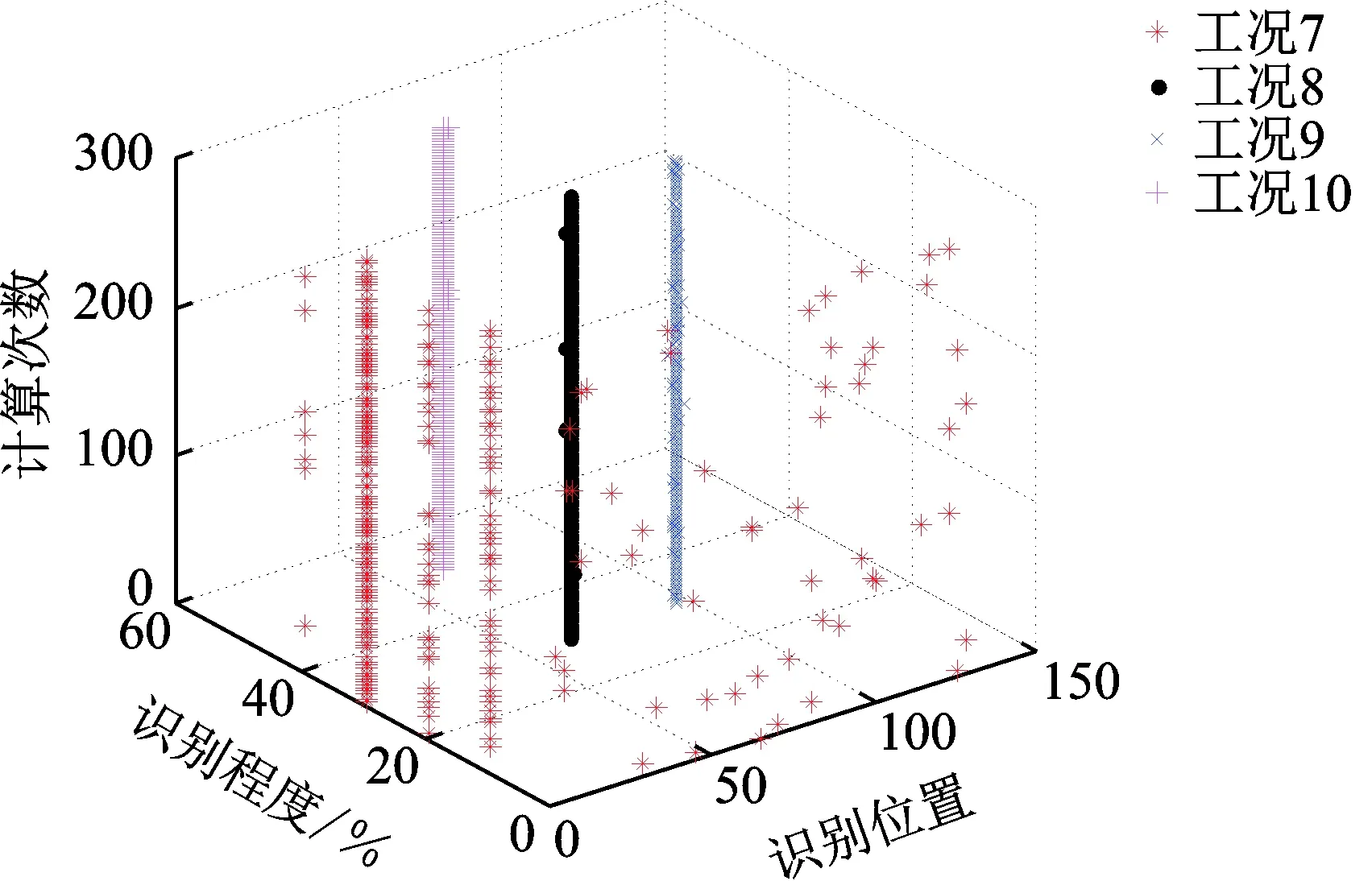
图9 多目标识别结果Fig.9 Results of multi-objective detection

综合以上单目标损伤位置、损伤程度及多目标损伤识别结果，可以看出GA算法对单个损伤单元的识别，基本能在20代以内识别成功。当损伤单元数量增加为两个且损伤程度均未知(待识别变量为4个)时，此时GA算法搜索空间域大小为(8×128)2≈105万，搜索空间域显著增大将带来识别效率的降低。假设损伤单元为第63，120单元，损伤程度分别为50%，30%，设定初始种群数量为50，最大遗传代数Maxgen为400，通过计算发现在400代损伤识别过程中，只在第252代找到最优解。由于GA算法搜索空间域增大而导致识别运算量增多，也增加了车桥有限元模型的计算耗时。可见，GA算法对更加复杂的损伤状态识别效率将有所降低，此时可考虑减小有限单元划分数量来初步识别损伤状态，或结合其他识别方法进行损伤初步识别，再运用GA算法进行二次识别以确定损伤状态。

4 结 论

1) 无论对于单目标识别(单个损伤位置或损伤程度)还是多目标识别(同时识别损伤位置和损伤程度)，采用笔者所提GA算法都能以较高的识别效率成功识别。

2) 对于单目标识别，经过多次独立重复计算发现，GA算法在识别过程中，搜索空间大小对识别效率产生较大影响。以本算例来看，当初始种群数量为4时，单个损伤程度识别搜索空间大小为8，基本在5代以内识别成功；单个损伤位置识别搜索空间大小为128，基本在20代以内识别成功。

3) 对于多目标识别，当对单个损伤位置和程度同时识别时，随着初始种群数量的增加，损伤识别成功率(EP1)显著提高，首次出现最优解平均迭代代数(EP2)明显降低。以本算例来看，初始种群数量取16较为合理，此时基本能在20代以内成功识别桥梁损伤，这为最大遗传代数的设定提供了一定依据。

4) 本研究中GA算法对桥梁跨中及3/4跨位置的损伤识别结果较桥梁端部更为稳定，端部损伤识别过程中可能会出现无法判断损伤发生桥梁左端还是右端的情况，可考虑采取二次识别以完善GA算法。