电磁力参数快速寻优的转子多频振动抑制研究

姚剑飞， 刘 亮， 王维民

(北京化工大学机电工程学院 北京，100029)

引 言

旋转机械结构复杂、运行工况苛刻，转子振动问题突出，且振动频率成分复杂和多样化，如不及时有效抑制过大的转子振动，可能导致振动状态将进一步恶化最终造成停车事故。因此，研究旋转机械转子复杂振动的主动抑制对大型旋转机械的长周期可靠运行具有重要的意义[1]。

对于旋转机械通过施加主动控制力抑制振动和噪声，受到了学者们的广泛关注。国内外学者采用主动悬架[2]，基于电流变液[3]、压电材料[4]及形状记忆合金[5-6]等作动器对转子振动进行主动控制研究做了大量工作。文献[7-9]介绍了国内外学者在电磁轴承支承的转子系统的振动主动控制方面的研究工作。Fang等[8]对于转子-电磁轴承系统中不平衡振动问题，提出了一种陷波滤波和前馈补偿算法，采用修正器自适应调整控制器增益和相位。Roy等[9]提出一种简单比例结合有限高频带微分的控制律，用于转子-电磁轴承系统的转子不平衡振动主动抑制。当前对于转子-电磁轴承系统的转子不平衡振动的主动控制研究相对较多，对于转子产生的具有多个频率成分的复杂振动的主动抑制研究则相对较少。文献[10-11]通过频率匹配控制信号实现了柔性转子-电磁轴承系统的多频振动的平行动态反馈控制，提出了一种基于转子离散振动成分反馈的鲁棒控制方法进行多频振动控制。Jiang等[12]提出了一种基于时域有限长脉冲响应滤波器的主动电磁轴承转子系统多频周期振动补偿方法。大多数研究集中在电磁轴承支承的转子系统中，在实际旋转机械中改变支承结构十分困难，而安装用于转子振动控制的作动器还有一定的可操作性，因此将电磁轴承仅作为作动器对转子振动进行主动抑制研究是十分必要的，目前这方面的研究文献相对较少。文献[13-15]将电磁轴承用于作动器进行转子振动的主动抑制研究，提出了转子单频及多频率成分振动的主动抑制方法。

为抑制转子-轴承系统的多频振动，笔者建立了转子-轴承-电磁作动器系统动力学模型，提出了一种电磁力参数快速寻优的转子系统多频振动主动抑制方法。该方法采用变步长寻优策略，快速获取电磁作动器控制电流的最佳参数。在转子上施加多个与转子振动频率相匹配的旋转电磁力，抑制转子复杂振动，并搭建实验装置进行了实验研究。

1 转子实验台动力学建模及分析

1.1 实验台简介

转子-轴承-电磁作动器系统实验台主要由轴、圆盘、电磁作动器、滑动支承轴承、传感器、驱动电机、数采及控制系统等组成。主要参数如表1所示，装置实物如图1所示。

图1 转子振动抑制实验台Fig.1 Test rig of rotor-bearings system with electromagnetic exciters

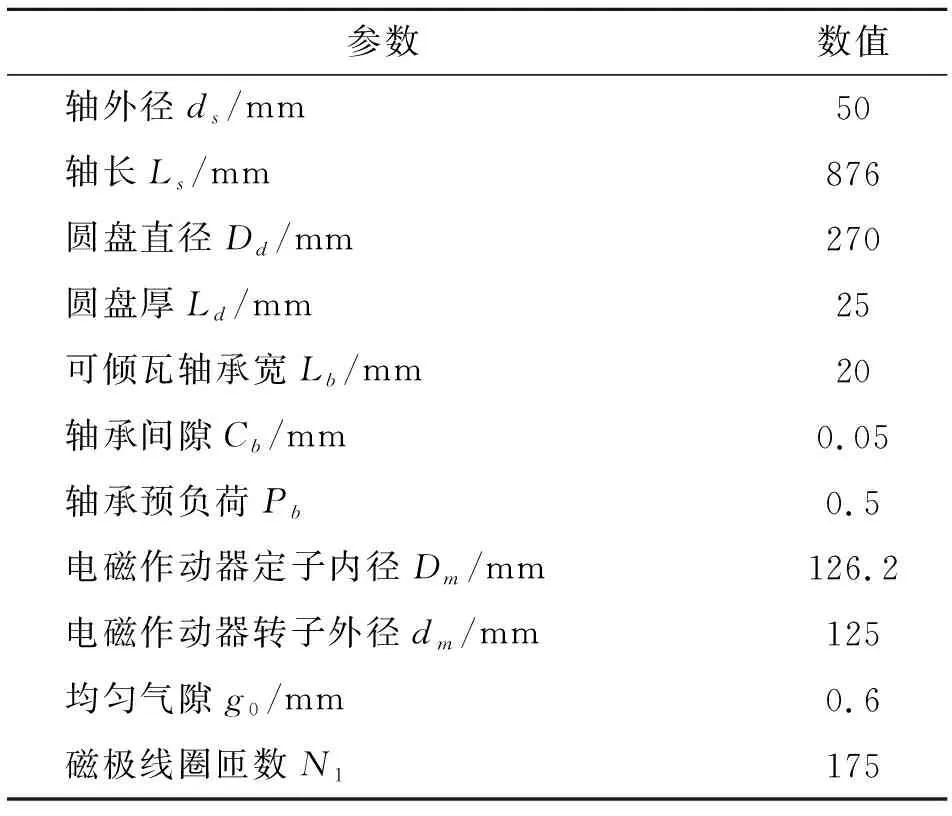
参数数值轴外径ds/mm50轴长Ls/mm876圆盘直径Dd/mm270圆盘厚Ld/mm25可倾瓦轴承宽Lb/mm20轴承间隙Cb/mm0.05轴承预负荷Pb0.5电磁作动器定子内径Dm/mm126.2电磁作动器转子外径dm/mm125均匀气隙g0/mm0.6磁极线圈匝数N1175

1.2 实验台动力学建模及分析

基于有限元法建立如图2所示的转子系统动力学模型为

(1)

其中：y为位移向量；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Q为广义力向量；Qmag为控制力向量。

(2)

图2 转子系统动力学模型Fig.2 The model of rotor-bearings system with electromagnetic exciters

基于该实验台转子系统模型，计算了可倾瓦滑动轴承刚度、阻尼特性以及系统的前3阶无阻尼临界转速及振型，如图3，4所示。计算得到的实验台转子系统一阶临界转速为4 820 r/min，实测转子系统的一阶临界转速为4 900 r/min左右，误差为1.6%，验证了模型的准确性。

图3 实验台转子系统轴承刚度、阻尼特性Fig.3 Dynamic stiffness and damping coefficients of bearing with the speed increase in test rig

图4 转子系统实验台的前3阶振型Fig.4 Critical speed shape of rotor-bearings system with electromagnetic exciters

2 电磁力参数快速寻优的多频振动抑制方法

2.1 转子-轴承系统多频振动抑制策略

基于系统干扰与响应是线性关系的假设，则激励力频率成分与相应的振动响应频率成分具有一一对应的关系。笔者采用电磁作动器产生的具有多个频率成分的电磁力来抑制转子的多频振动。其方法是通过给电磁作动器施加试探控制电流，在线分析转子振动响应，将振动幅值作为寻优目标函数，搜索电磁作动器线圈控制电流的最优幅值和相位，使转子振动响应幅值最小，进而电磁作动器产生与转子振动频率相匹配的电磁力，抑制转子的多频振动。笔者提出的快速寻优策略主要有两大步骤：a. 确定多频电磁控制力的正、负作用区域；b. 在正作用区域内采用小步长搜索方式，准确定位最佳的控制电流相位和幅值。该策略缩小了搜索空间，提高了搜索效率，为转子多频振动的快速抑制提供了可能。

2.2 电磁力参数变步长快速寻优算法

2.2.1 寻优目标函数建立

令转子系统上有k个测点，s个电磁作动器，设具有m个频率成分的激励作用在第j个节点处，将此节点处的第i个频率成分的激励激起的响应幅值Zji(Aji,φji)作为目标，得到寻优模型为

(3)

其中：Aji={Aji1,Aji2,,Ajih}T，为线圈电流的幅值；φji={φji1,φji2,φjih}T，为线圈电流的相位；h为线圈数；A0为线圈所能承受的极限电流。

令第j个节点处的电磁作动器线圈电流幅值向量为A，初始相位向量为φ，则有

A={Aj1,Aj2,,Ajm}T

(4)

φ={φj1,φj2,,φjm}T

(5)

式(3)的寻优可行域为

(6)

令

Z(A,φ)={Zj1(Aj1,φj1),Zj2(Aj2,φj2),,Zjm(Ajm,φjm)}T

(7)

则第j个截面处的寻优目标函数为

J=min(A,φ)∈XZ(A,φ)

(8)

2.2.2 寻优步长确定

电磁控制力作用到转子上，对转子原始的振动起到抑制或加剧的作用，关键取决于控制力与原始激振力间的相位关系。定义起抑振作用的控制力相位区域为正作用区域，起激振作用的控制力相位区域为负作用区域。

图5 电磁力参数快速寻优示意图Fig.5 The diagram of fast optimizing search algorithm about the electromagnetic force

令

则有

(9)

由图5可知，用βj的取值表示原始激振力与试探控制力合成后的合力与原始激振力的大小关系：

2.2.3 快速寻优流程

采用坐标轮换与变步长相结合的多目标多变量寻优方法。对于每个坐标下的寻优，首先，进行控制电流相位的大步长搜索，通过1～2次相位跳转，试探电磁力就可进入正作用区域；然后，采用小步长搜索方式进行精确搜索；最后，完成控制电流幅值的等步长寻优，如图6所示。令第j个截面处的第i个频率成分振动幅值为Zji；初始状态为Zji0；初始幅值和相位为Aji0和φji0。

图6 快速寻优流程图Fig.6 Flow chart of the fast optimizing search algorithm

ΔZji1=Z(Aji0,φji1)-Z(Aji0,φji0)

(10)

根据ΔZji1的符号和大小确定是否进入抑振区。如未进入抑振区，则进行第2次大步长搜索。

令φji2=φji1+ΔφA，则

ΔZji2=Z(Aji0,φji2)-Z(Aji0,φji1)

(11)

最多经过两次大步长搜索即可进入抑振区域，记录该振动状态下的参数φji的值。

最后，进行幅值寻优，令Aji1=Aji0+ΔAji，ΔAji为幅值寻优步长，则

(12)

(13)

以此类推，得到最佳控制状态，即

(14)

3 实验及分析

根据上述分析编写了快速寻优策略的程序，在转子振动抑制实验台上进行了实验验证。分析结果如下： a.提出的快速寻优策略能够及时确定电磁力参数，实现转子多频振动的快速、有效抑制；b.如图7所示，该策略对控制过程中出现的超调现象还无法避免；c.如图8所示，转子各个频率的振动成分在不同转速下的抑制效果略有不同，其中的深层次机理问题还需进一步探究；d.与文献[15]提出的整周寻优策略对比，快速寻优策略的控制时间明显少于整周寻优策略，如图9所示。

图7 转速分别为1 200，1 500和1 800 r/min时的振动抑制效果Fig.7 Rotor displacement response at the speed of 1 200, 1 500 and 1 800 r/min before and after controller activation

图8 转速分别为1 200，1 500和1 800 r/min时各频率成分的振动抑制效果图Fig.8 Rotor vibration magnitude spectra at rotational speed of 1 200，1 500 and 1 800 r/min with and without control of Ω×1,2,3,4 frequencies

图9 多频振动抑制的整周寻优与快速寻优控制时间对比Fig.9 Time of vibration control at different rotational speeds for the whole circle search algorithm and fast optimizing search algorithm

4 结束语

建立了安装有电磁作动器的转子系统动力学模型，提出了一种基于电磁力参数快速寻优的转子多频振动主动抑制方法。采用控制电流相位变步长搜索策略，快速获取控制信号参数，并通过实验验证了该方法的有效性。相比等步长的整周寻优策略，快速寻优策略用时更短，不足是该策略对控制过程中出现超调现象还无法避免。总之，本研究方法能够实现转子多频振动主动抑制，缩短了控制时间，实验效果明显。