基于Hilbert变换的裂纹叶片时变物理参数识别

孙佳兴， 曹树谦,3， 郭虎伦,3， 李利青,3

(1.天津大学力学系 天津，300072) (2.天津市非线性动力学与控制重点实验室 天津，300072) (3.天津大学内燃机燃烧学国家重点实验室 天津，300072)

引 言

在航空发动机中，压气机叶片和涡轮叶片是关键零件之一。由于工作环境恶劣，叶片故障占到发动机零件疲劳故障的30%～40%，严重影响了发动机的安全[1-2]。因此，越来越多的研究致力于寻找结构非破坏性的裂纹检测手段，依靠振动的裂纹检测技术提供了一种快速有效的方法[3]。此类方法的应用前提是建立一个合理的能够反映损伤机理的动力学模型，这样得到的测试信息才能反映结构真实的损伤特征。

裂纹叶片在振动过程中会出现“张合”过程[4]，使裂纹叶片的弯曲刚度出现时变特征，这是裂纹结构振动出现非线性现象的主要原因。然而，真实描述这个过程的开合函数却很难获得，以往的研究对于呼吸裂纹的处理模型大致分为方波开合函数和曲线型开合函数两种。前者是为了简化计算，将裂纹的开合过程描述成方波函数[5]，即在振动的前半周期处于全开状态，后半周期则全闭。方波函数描述的开合过程是阶跃性的。在之后的研究中，通过实验证明了裂纹由开启到闭合是经历平滑的过渡过程。依据这个事实，文献[6]提出了用余弦函数模拟部分开启时的状态。与前者相比，能够更合理地描述开合过程，但也只是近似模拟。杨海燕等[4]采用余弦函数模拟裂纹的开合过程，以带疲劳裂纹悬臂梁为例，研究疲劳裂纹对叶片固有频率及强迫振动响应的影响，并进行裂纹试件实验。刘文光等[7]考虑了振动与疲劳的耦合，通过数值方法计算得到裂纹摩擦阻尼对疲劳裂纹扩展的影响。Rezaee等[8]把悬臂梁裂缝处刚度降低等效为一刚度变化的弹簧，通过梁端振幅控制弹簧刚度大小，用能量平衡法分析了裂纹梁每一时刻的动态响应。

目前，呼吸裂纹模型大多是在一些准静态实验现象的基础上，用简单函数描述裂纹的开启-闭合行为，很难还原实际的物理参数变化规律。裂纹在运动过程中存在各种复杂且相互耦合的因素，以正问题的方法将其确定比较困难。笔者从反问题出发，将基于动态响应测量的物理参数识别应用于裂纹结构，在文献[9-11]的基础上，针对裂纹叶片的实际背景，分析实验测得的响应和激励信号，验证基于Hilbert变换的方法可以有效识别时变刚度和阻尼。根据实验发现的新现象对原物理参数模型进行修正，研究新模型中的各参数随外界条件的变化情况。数值和实验结果对比表明，修正后的模型更加符合真实裂纹的开合过程。

1 理论基础

1.1 基于Hilbert变换的参数识别方法

对于单自由度系统，时变刚度和阻尼的表达式[10]为

其中：m为系统质量。

h0(t)和ω0(t)分别为

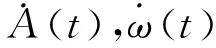
ξ(t)和η(t)为激励力和响应比值的实部和虚部

其中：F(t)和Y(t)分别为外激励和位移响应经Hilbert变换后得到的解析信号，公式中各参数的表达式详见文献[10]。

1.2 呼吸裂纹叶片模型

不考虑叶片的旋转运动，用一个带裂纹的等截面悬臂梁研究其振动规律。一个均质的悬臂梁，长度为l，裂纹位置如图1所示。外激励形式为正弦函数。

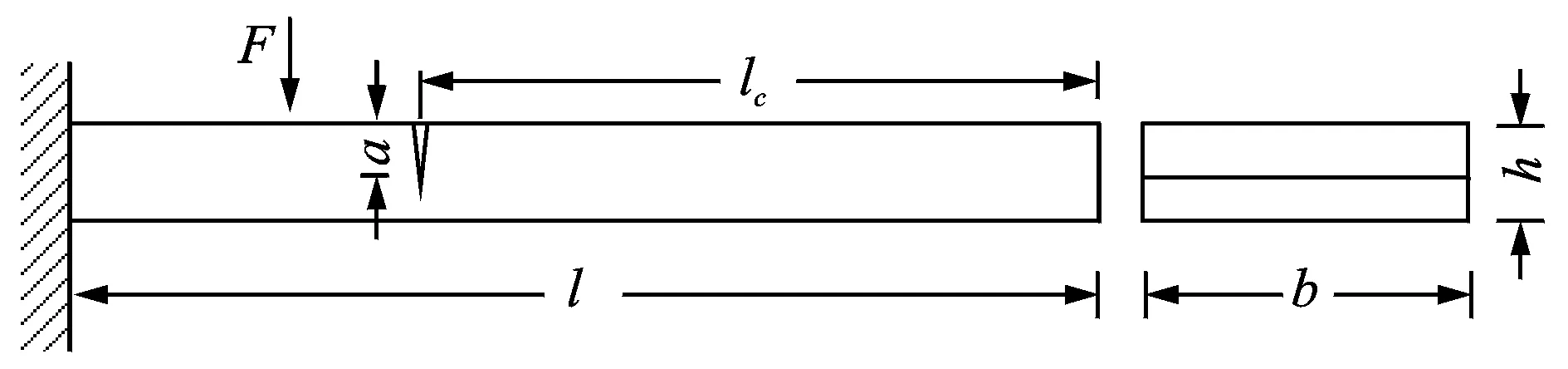
图1 裂纹悬臂梁Fig.1 The cracked cantilever beam

本研究的主要目的在于获得由于裂纹开合引起的物理参数时变特性，揭示叶片作为一个整体的动态行为，根据实际情况可以认为系统的外激励频率应与系统第1阶模态频率相接近。为了简化计算，只考虑第1阶模态对裂纹叶片振动性态的影响，将悬臂梁简化为单自由度系统。在实际操作中总会存在测量误差，需要测量的参数越多，累计的误差越大，简化为单自由度降低了研究参数的数目，提高参数识别精度。

强迫振动的系统运动方程为

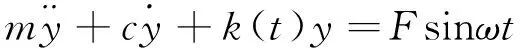
(7)

其中：c为阻尼系数；F为激励力幅值；y为自由端的横向位移;m为梁的广义质量且m=0.228m′l；m′为梁单位长度质量。

余弦开合模型是将时变刚度表示为简单周期函数，形式[6]为

其中：ω为外激励频率；kO和kC为梁完全张开和闭合时的刚度

其中：C为无裂纹梁的柔度；ΔC为由于裂纹存在导致梁柔度的改变量；I为截面惯性矩；E和ν为材料的弹性模量和泊松比；b和h分别为梁的宽度和厚度；lC为裂纹到根部的距离。

(14)

其中：a为裂纹深度。

2 裂纹梁物理参数识别实验

笔者设计了悬臂梁实验，验证基于Hilbert变换的识别方法能够有效识别裂纹结构的时变物理参数，并将识别结果与现有文献中的余弦开合函数模型进行对比分析。

2.1 实验装置和参数识别结果

如图2所示，搭建了用于物理参数识别的裂纹悬臂梁实验台。试件裂纹采用文献[12]的制作方法：用数控线切割机预先加工1.80 mm深的槽，槽宽介于0.20～0.23 mm之间，然后用胶单边固定0.20 mm的相同材质金属片，用来模拟真实裂纹。虽然与实际疲劳裂纹有差距，但能够较好控制裂纹的深度和宽度。

图2 裂纹悬臂梁实验台Fig.2 Experimental equipment of cracked cantilever beam

实验采用的悬臂梁基本参数如表1所示。在自由端安装加速度传感器，激振点到根部的距离为87.0 mm，激励频率为10 Hz，幅值为3.20 N，外激励的时频曲线如图3所示。自由端的加速度响应和频谱图如图4所示。

表1悬臂梁基本参数

Tab.1Physicalparametersofthecantileverbeam

l/mmb/mmh/mmlc/mm390.016.04.0259.0a/mmE/(N·m-2)νρ/(kg·m-3)1.802.1×10110.276 686

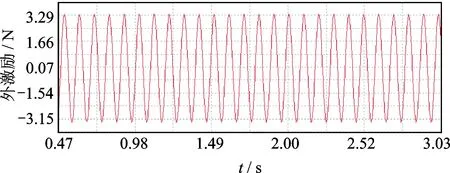
图3 外激励时域图Fig.3 The time history of external excitation

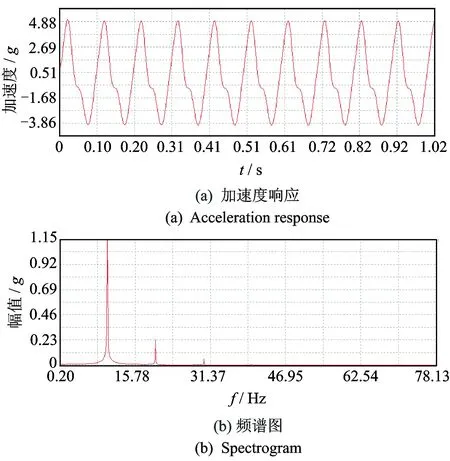
图4 自由端响应信号Fig.4 The signal of the free end

可见，悬臂梁自由端的加速度响应有明显的波形畸变，且频谱图中出现了二倍频和三倍频。在文献[13-14]中，呼吸裂纹的非线性行为也具有相似的现象。获得自由端的响应和激励力的信号后，笔者用基于Hilbert变换的参数识别方法进行识别，结果如图5所示。

图5 物理参数识别结果Fig.5 The result of parameter identification

从图5(a)可看出，通过识别得到的刚度随时间变化更接近余弦函数，刚度的波动范围在863.01～944.09 N/m之间。根据式(10)，(11)计算得到裂纹完全闭合时的刚度为919.59 N/m，完全张开时的刚度为890.32 N/m，二者的误差在3.07%以内。基于Hilbert变换的方法在识别时变物理参数的过程中，阻尼系数的估计精度小于刚度系数的估计精度[10]。在阻尼比较难测量的实际情况下，图4(b)的识别结果可以作为一个参考值，阻尼系数的均值为0.14 Ns/m。因此，实验中的裂纹制作方法可以模拟真实裂纹，Hilbert变换的方法可以有效识别裂纹产生的时变刚度和阻尼。

2.2 裂纹结构时变刚度模型改进

对图5(a)中刚度的时域图进行快速傅里叶变换，得到其频域图，如图6所示。发现刚度在随时间变化的过程中，由两个频率的余(正)弦波叠加而成，其中低频与强迫激励的频率相同，高频为低频的2倍。以往文献中的余弦模型用简单的单周期函数模拟裂纹开闭过程，不能完全反应真实的裂纹开合过程。根据两个峰值对应的相位差情况，笔者提出一种改进的余弦刚度模型

k(t)=kO+kΔC(1+cosωt-γsin2ωt)

(15)

其中：kO为裂纹完全张开时的刚度；kΔC为刚度变化量；γ为裂纹刚度变化过程中，高频幅值与低频幅值的比值。

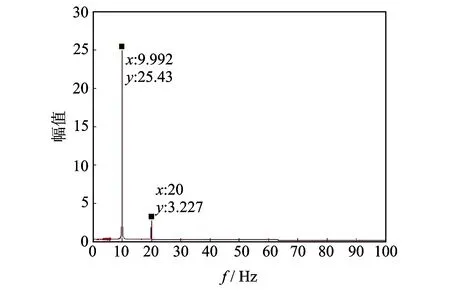
图6 时变刚度频谱图Fig.6 The spectrogram of the time-varying stiffness

3 外界条件对识别参数的影响

3.1 激励力幅值

激振频率为10 Hz，激励力的幅值分别为3.30, 5.28, 6.25和7.40 N，其他实验条件不变，时变刚度识别结果如图7所示。可以看出，各激振力下时变刚度的识别结果基本相同，误差主要体现在幅值上。为了定量描述这种差异，采用最小二乘法拟合式(15)中各参数值，如图8～10所示。可见，在不同外激励幅值条件下，kO和kΔC的识别结果基本保持不变。由式(11)计算的kO理论值与实验拟合值一致。外激励幅值对γ值的影响比较小，基本成一条水平直线，即刚度随时间变化的过程中，高频所占的比值不会随着外界激振力幅值的改变而变化。

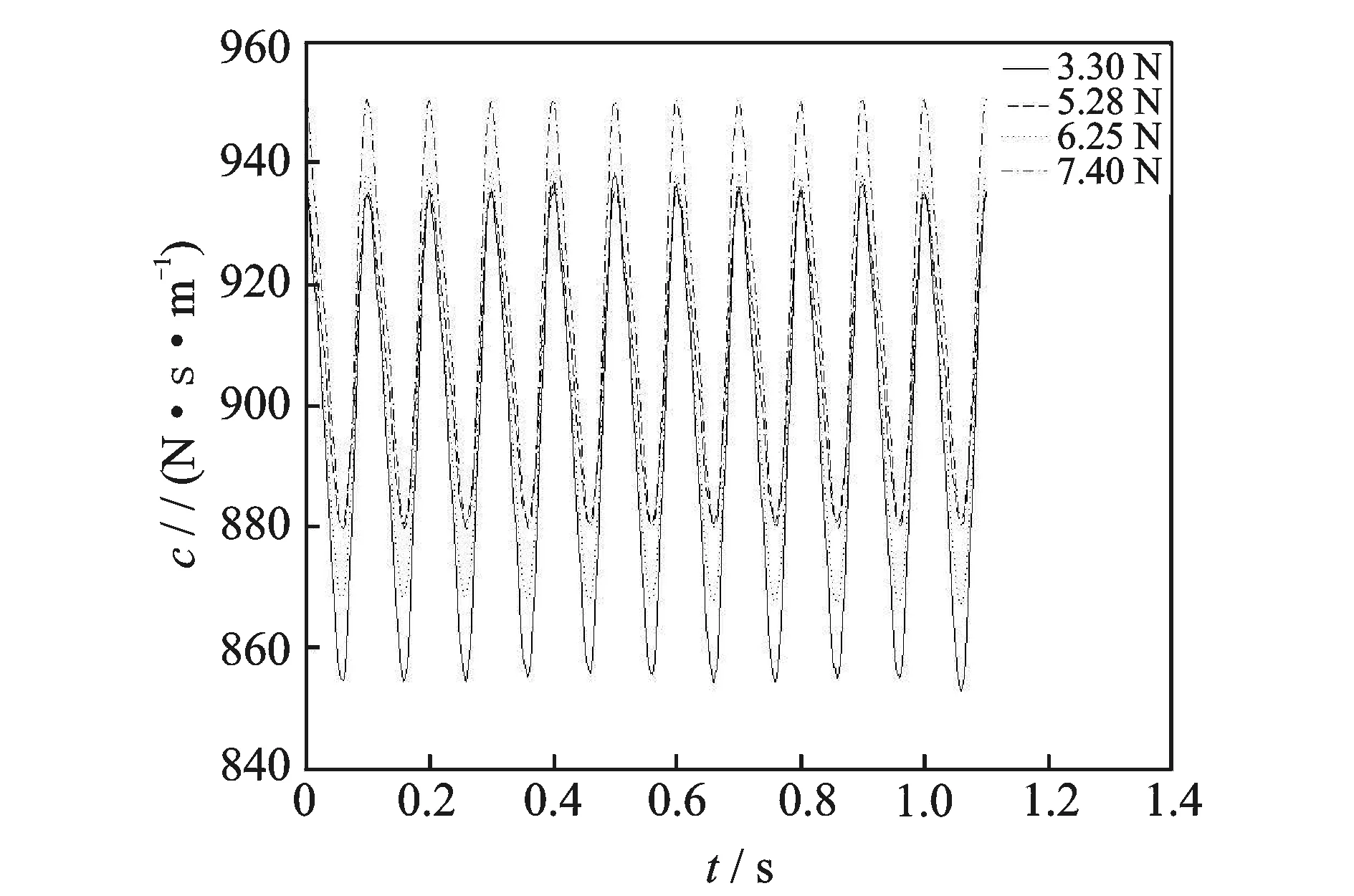
图7 不同激振力幅值下的刚度识别结果Fig.7 The stiffness identification results under different excitation amplitude

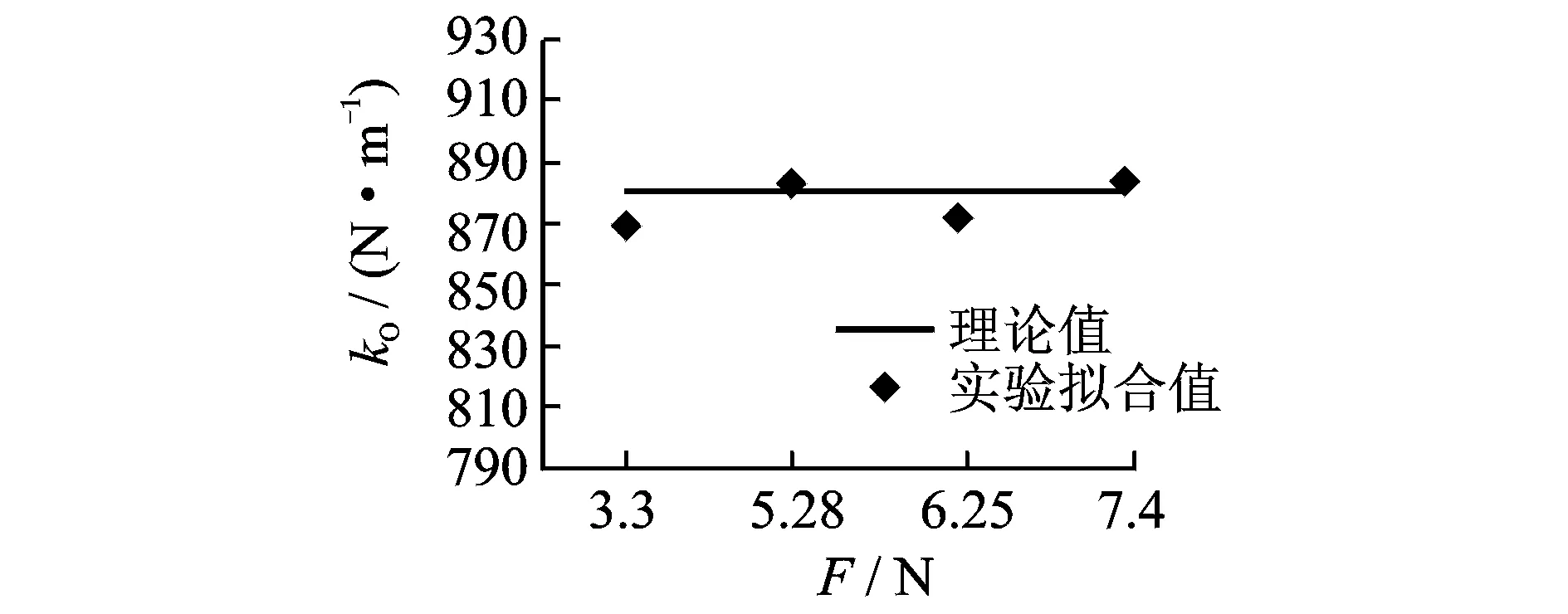
图8 不同激励幅值下kO值Fig.8 The value of kO under different excitation amplitude

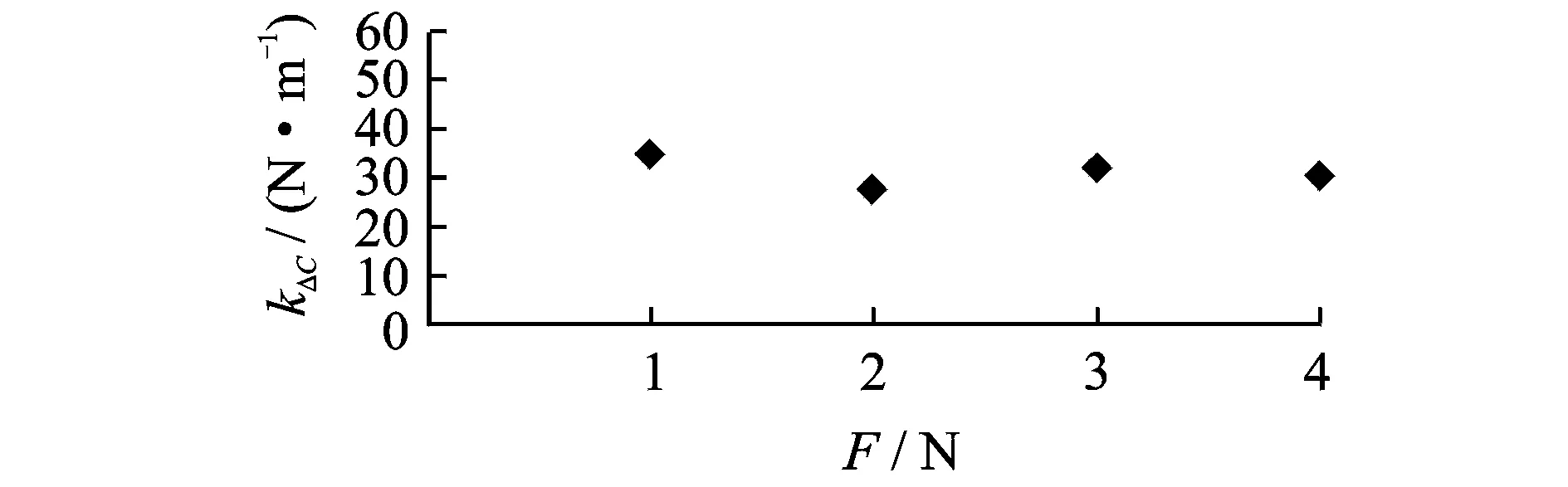
图9 不同激励幅值下kΔC值Fig.9 The value of kΔC under different excitation amplitude

图10 不同激励幅值下γ的拟合值Fig.10 The fitted value of γ under different excitation amplitude

3.2 激励频率

测得悬臂梁的固有频率为15.87 Hz，研究激振频率小于固有频率的情况。固定外激励力幅值为6.29 N，激振频率分别为5，7，10和13 Hz。采用相同的处理方法得到各参数的拟合结果如图11～13所示。

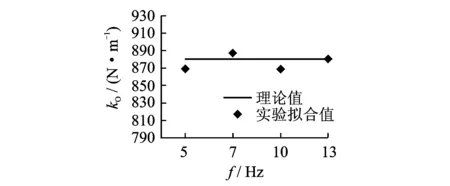
图11 不同激励频率下kO值Fig.11 The value of kO under different excitation frequency

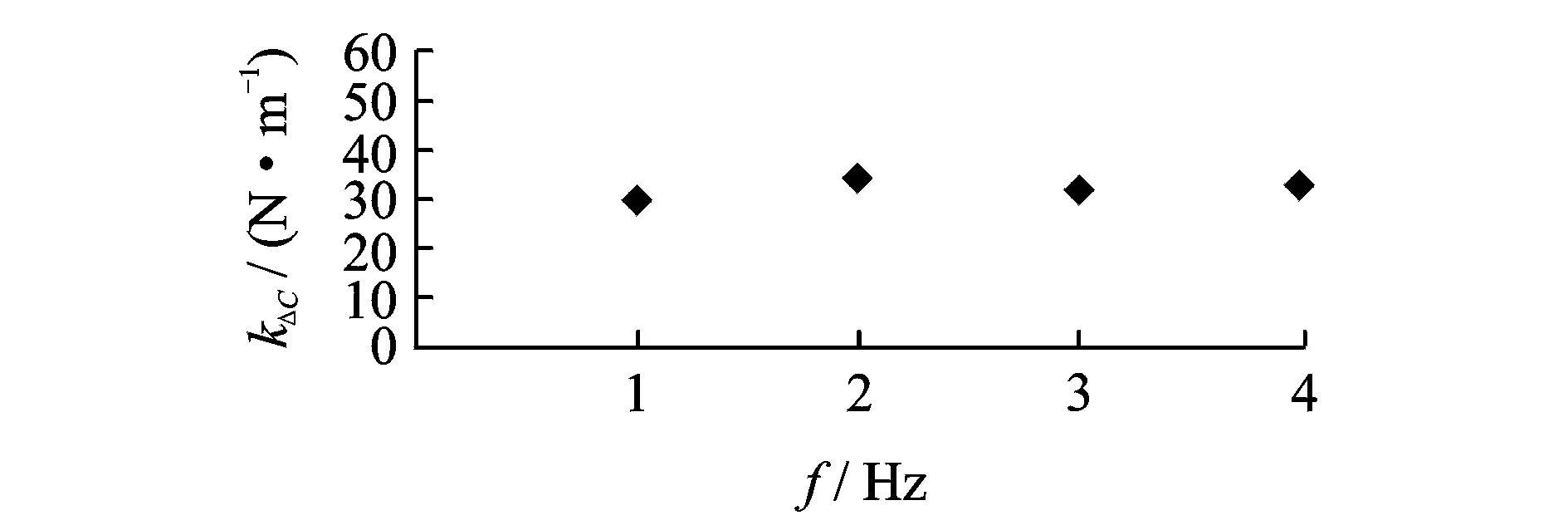
图12 不同激励频率下kΔC值Fig.12 The value of kΔC under different excitation frequency

图13 不同激励频率下γ的拟合值Fig.13 The fitted value of γ under different exciting frequency

从图11，12可以看出，kO的实验拟合值在理论值附近，且kO和kΔC的实验拟合值对外激励频率变化并不敏感。图13的结果显示，在不同的外激励频率情况下，γ值的拟合结果基本不变，呈现一条水平直线，即刚度随时间变化的过程中，高频所占的比值不会随着外界激振频率的改变而变化。

通过这两组实验可以发现，修正后的模型中，参数γ与外界激励的频率和幅值无关，是反应裂纹结构运动过程特性的物理量。

4 数值计算

为了验证哪个模型更符合实际情况，笔者将修正前和修正后的模型代入运动方程，分别用Matlab进行数值计算，将得到的响应与实验结果进行对比。

式(7)为运动方程，时变刚度k(t)的表达式分别为式(8)和式(15)。将各参数代入表达式，γ取均值0.14，用四、五阶Runge-Kutta法计算响应，得到的结果如图14，15所示。可见，两个模型得到的自由端时域图差别不大，频谱图有较大区别：由余弦刚度模型得到的响应频谱图存在工频和二倍频；而改进的余弦刚度模型计算得到的频谱图存在明显的工频，二倍频和三倍频。同实验得到的图3(b)对比可以发现，改进后的余弦刚度模型更加符合真实的裂纹结构开合过程，对于实验中响应出现的三倍频，原来的余弦模型并不能很好的解释，而改进的模型可以解决这个问题。

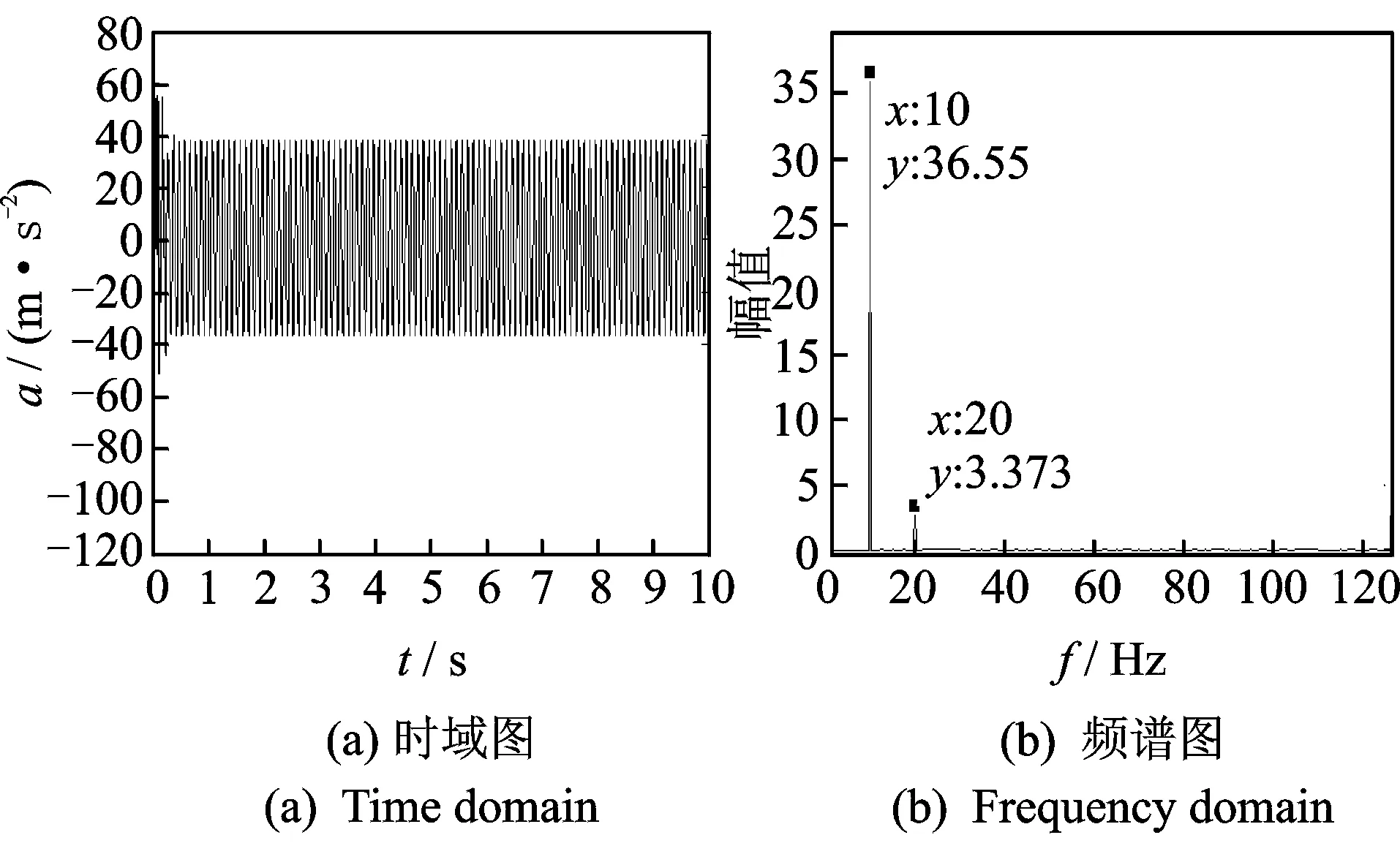
图14 余弦刚度模型响应Fig.14 The response of the cosine stiffness modal

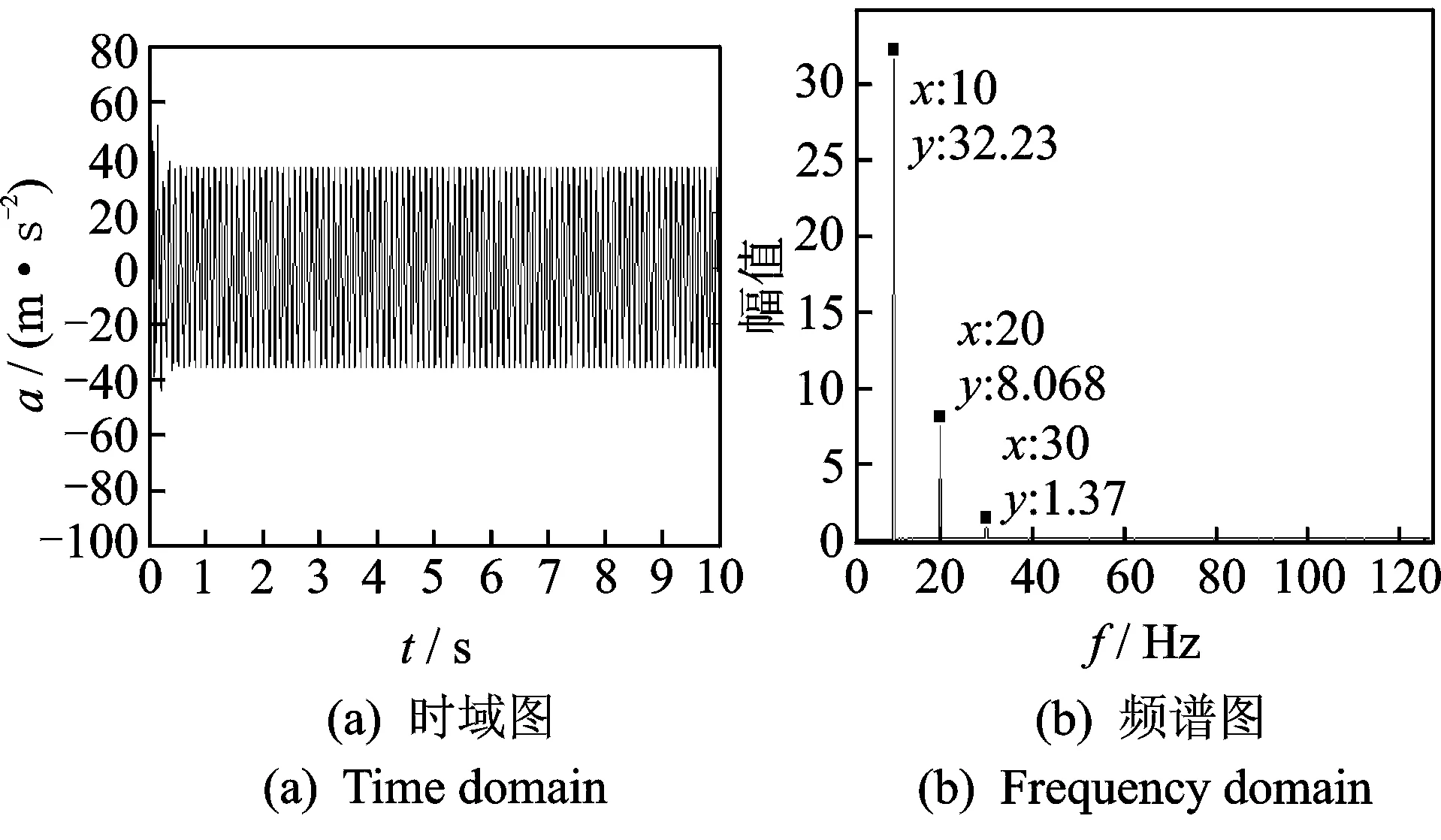
图15 改进余弦刚度模型响应Fig.15 The response of the modified cosine stiffness modal

5 结 论

1) Hilbert变换方法能有效识别时变系统结构物理参数，在质量已知的情况下，测得系统的响应和激励信号，可以较好识别裂纹结构时变刚度和阻尼。

2) 识别得到的时变刚度由两个频率的余弦波叠加而成，基于实验结果对原有模型进行修正，更加符合真实裂纹的开合过程。

3) 改进模型中的参数γ与外界激励的频率和幅值无关，是反映裂纹结构在运动过程中自身特性的物理量。

4) 通过数值计算两种模型下的动力学响应，并与实验结果对比，验证了提出的改进余弦模型更加符合真实情况，优于以往的余弦模型。