农户供应不确定下龙头企业采购决策研究

税文兵，杨汉卿，何 民

（昆明理工大学 交通工程学院，云南 昆明 650500）

0 引言

订单农业，又称合同农业或契约农业，是指在农业生产之前，农户与企业或中介组织签订具有法律效力的确定双方权利与义务关系的产销合同，农户根据合同组织生产，企业或中介组织按合同收购农户生产的产品的一种农业协同经营形式[1]。从供应链管理角度看，订单农业本身就是一种通过契约实现买方（农业企业）和卖方（农户）之间协调的农产品供应链，因此在学术界又被称为订单农业供应链[2]。订单农业供应链不仅能够显著增加农户收入[3]，而且还有助于实现农业企业原材料的稳定供应，因此在全世界范围内都得到广泛推广和普及[4]。在我国，超过180亿公顷的土地是在订单农业供应链模式下耕种的[5]。

然而，在订单农业供应链实际运营中，农户实际供应量与合同签约量相违背成为困扰农业企业的重要问题。如2010年10月，乌鲁木齐洋葱普遍减产，市场洋葱价格上涨，签订契约的种植农户为了获得更高的经济利益，普遍抬高洋葱的收购价格，或者转卖给其他高价收购商，造成了农户大规模的违约现象，洋葱的供应不确定结果导致洋葱的收购方以高于合同价的市场价格收购，造成了市场及收购方巨大的经济损失[6]；2012年，陕西省西眉县奇峰公司在四、五月份和猕猴桃果农签了订单交了定金，到10月份收购季，当市场价格高于合同价的时候，果农把订单合同丢到一边，将猕猴桃卖给其他高价收购商，奇峰只好与果农重新商谈价格；而且，果农签约后，由于技术条件有限，果农无法达到订单标准的质量，这些猕猴桃数量或质量供应的不确定最终导致公司巨大的经济损失[7]。签约农户实际供应不足，企业就要承担缺货带来的额外采购成本或直接的销售损失；签约量过多，则会发生较高的库存管理成本或农产品超过保质期腐烂变质损失。因此，如何确定恰当的签约量成为影响农业企业经济效益和订单农业供应链稳定发展的重要问题。

目前，针对订单农业供应链中农产品供应问题的研究，主要集中在如何通过完善农户和企业之间的契约降低故意违约率[8-12]，较少涉及签约量的研究。订单农业生产具有典型的单周期、多源供应（多个农户与农业企业签定契约）和实际产出不确定的特点，因此，订单农业供应链中的签约量决策问题与供应不确定下的多源（超过两个供应商）报童问题类似。Agrawal等首先研究了产出随机下有多个供应商的报童问题，假设供应商的实际供应服从正态分布，考虑了供应商的固定签约成本，建立了以期望利润最大化为目标，同时对供应商的数量和每个供应商的签约量进行决策的数学规划模型[13]。Dada等同样研究了随机供应下的单周期多源报童模型，假设需求也是随机的，但没有考虑供应商的固定签约成本[14]。Federgruen等建立了两种随机供应下的多源采购模型：一是以采购成本最小化为目标，确保需求以一定的概率被满足；二是以总的期望成本最小为目标，同时对每个供应商的采购量进行决策[15]。两个模型都没有考虑固定签约成本和供应商生产能力。Yang等设计了基于非线性规划技术的算法求解随机多源供应下的报童模型[16]。Merzifonluoglu等同时考虑了供应商的固定签约成本和生产能力约束，模型除对订货量进行决策外，还对供应商的选择进行决策[17]。

上述供应不确定下的多源报童问题研究是在一般生产制造背景下，从对基本报童模型拓展的角度展开，并不能满足订单农业供应链中最佳签约量决策的需要。这主要表现在三个方面：一是没有考虑农户（供应商）最小生产量的约束；二是模型的目标函数没有包含农业企业对农户的生产服务成本；三是缺乏有效算法求解存在大量农户时的模型。本文针对这些不足，建立考虑农户固定签约成本、农户生产服务成本和生产能力上下限约束，同时对农户选择和订单大小进行决策的数学规划模型；设计能够在较短时间内求解大规模算例的遗传算法和粒子群算法，并对两种算法的性能进行比较。本文的研究一方面有利于完善供应不确定下的多源报童模型研究；另一方面可以帮助农业企业在农户供应不确定下更好地确定签约量。

1 模型构建

1.1 问题描述

农业企业为满足未来零售市场的需求，在农产品的生产和销售季节到来之前，与农户签订双方同意的收购订单。该订单规定了农户的种植规模、种植地点、交售农产品的时期，同时也明确了农业公司的收购价格、种苗价格、技术服务等内容。许多自然和人为的因素会导致在农产品收获期，农户实际提供的农产品数量与根据合同规定的种植规模测算出来的数量相差较大，进而给农业企业带来经济损失。为了降低农产品供应不稳定带来的不利影响，农业企业在与农户签订订单时，需要根据农户的供应特征对其进行筛选，并对筛选出来的农户分配不超过其生产能力的订单。在这一过程中，需要考虑农户固定签约成本、农户生产服务成本、不足需求的缺货成本、过多需求的存货成本和农产品采购成本之间的平衡。

1.2 模型参数和假设

在构建模型之前，提出如下参数假设：

（1） 农户i的实际供应量为签约量与随机系数γi（实际供应比例） 的乘积，随机系数0≤γi≤1，反映了农户实际供应农产品数量与签约量之间的差距，并服从均值为μi，标准差为σi的正态分布；

（2）采购成本为单位采购成本c与企业实际收到的农产品数量的乘积；

（3）缺货成本为单位缺货成本s与缺货量的乘积，缺货量等于需求D与实际供应量的差值；

（4）当实际供应量大于需求时，农业企业需要投入额外从资金进行保管，或者由于超过保质期丧失使用价值，此时产生单位成本为h；

（5）农户固定签约成本与签订的农户数量成正比，单个农户的签约成本为a；

（6）农产品生产服务成本与农户签约量成正比，单位签约量的生产服务成本为k；

（7）考虑农户土地规模限制，单个农户签约量不能低于最小值Mi，也不能超过最大值Ci；

（8）是否与农户签约及签约量的大小是模型的决策变量，分别用Xi（取1表示与农户i签约，否则取0）和Qi表示；

（9）农户的履约行为是独立的。

1.3 模型建立

（1）实际总供应量的均值和标准差

根据正态分布的特性，所有农户实际总的供应量Y也服从正态分布，其均值和标准差的计算如下：

其中：式（1）为实际总供应量的均值；式（2）为实际总供应量的标准差。

（2） 采购成本的均值

采购成本均值的计算如下：

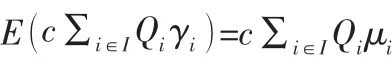
（3） 缺货成本的均值

缺货成本为smax｛ D-Y, ｝0，其均值如下：

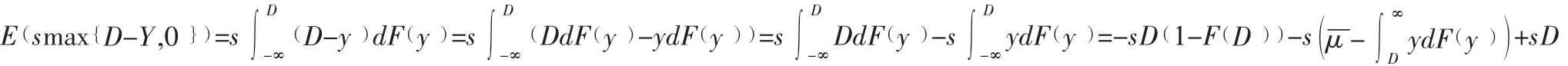
其中：F（·）为概率分布函数。

（4）仓储和耗损成本均值

库存保管和耗损成本为hmax｛ Y-D,｝0，其均值计算如下：

综上，订单农业供应链中农户选择和订单分配模型如下：

其中：式（3）为模型目标函数，包括农户签约成本、生产服务成本、期望采购成本、期望缺货成本和期望库存保管和耗损成本；式（4）表示单个农户签约量不能超过其生产能力；式（5）表示总的签约量不能低于需求量；式（6）表示单个农户的签约量不能小于规定值；式（7）是决策变量的取值范围。

2 算法设计

上述模型目标函数中含有积分项，决策变量中包含0、1整数变量和非负连续实值变量，因此模型属于典型的混合整数非线性规划模型。模型决策变量的组合特性，导致当决策变量数量较大时，很难在较短时间内找到精确解。因此，对这类模型的求解，常采用智能优化算法，如遗传算法（Genetic Algorithms，GA）、粒子群优化（Particle Swarm Optimization，PSO）算法等。本文分别采用遗传算法和粒子群优化算法求解模型，并通过对不同规模算例求解，对两种算法进行比较。

2.1 遗传算法设计

（1） 编 码

一条染色体由农户的选择变量X和签约量Q组成。其中，X自身就是0、1变量，Q是实值变量。为了便于交叉和编译，统一采用二进制编码的方法。因此，仅需将“十进制”变量Q转换为二进制变量，二进制变量的位数由下式决定：

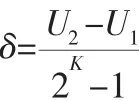
式中：U2、U1为连续变量的上、下界；k为每一个连续变量表示为二进制时的位数；δ为连续变量转换为二进制时的精度要求。签约量的上届U2为总的需求D，下界为0，精度要求为1位。

（2） 初始种群产生

初始种群的产生采用随机的方法产生。由于对约束处理采用惩罚函数的方法，因此，对于每一条随机生成的染色体不需要进行可行性验证。

（3） 适应度函数

采用惩罚函数的方法将有约束问题转换为无约束问题，适应度函数为[18]：

其中：f（x）为原优化问题的目标函数；R为惩罚系数；gk（x）为原优化问题中的第k个不大于0的不等式约束，总的不等式约束个数为p；hl（x）为原优化问题中的第l个等式约束，总的等式约束个数为m。

（4） 遗传操作

包括交叉、变异和选择。

（5） 终止条件

当连续10次迭代的种群均值或种群最小值的标准差不超过规定的数值，且获得最小值满足所有的约束条件时停止迭代。如果上述条件在规定的最大迭代次数内都不满足，则程序停止迭代。

2.2 粒子群算法设计

粒子群算法通过模拟鸟群捕食过程中相互协作从而找到最优路径的行为以获取最优解，关键步骤如下：

（1） 粒子群初始化

包括粒子的编码和群体的生成。此处，粒子统一采用上文遗传算法中染色体的二进制编码，粒子群随机生成，规模为150个。

（2） 确定适应度函数

适应度函数如式（8），同样采用惩罚函数的方法处理约束。

（3） 速度和位置更新

适应度函数确定后，需要计算各个粒子的适应度值，并对个体极值和群体极值更新。然后，对粒子速度和位置进行更新。在离散空间下，速度和位置的更新公式如下[19]：

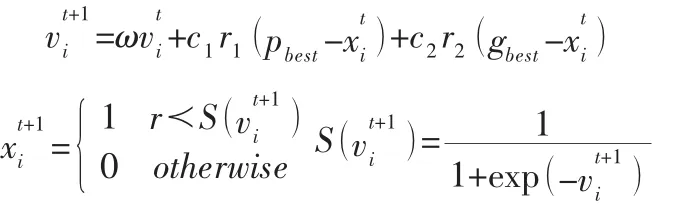
其中：ω称作惯性权重，c1、c2为常数，称作学习因子（也叫加速系数），r1、r2是两个0到1之间的随机数。

（4） 终止条件

与遗传算法终止条件相同。

3 算例分析

3.1 算例设计

为了检验模型的有效性和对两种算法的求解效能进行比较，设计了15个不同规模的算例。这些算例中，总的需求根据历史数据预测得到，算例中取值为2 000kg；单位采购成本为合同规定的最低收购价，取值为8元/kg；单位缺货成本是当农户实际总的供应量不能满足需求时从现货市场购买所产生的成本增加值或者是不能满足需求直接产生的销售损失，取值为9元/kg；农户实际供应比例均值和标准差根据历年农户的实际供应情况统计得到，分别为0.86和0.08；供应关系建立成本和生产服务成本可从农业企业的财务报表得到，分别为1 000元/户、5元/kg；仓储成本是当实际供应量大于需求量时产生的库存管理成本，也包括折价销售或腐烂变质带来的损失，取值为3元/kg；单个农户的最小生成数量取值为5kg/户。

不同算例的区别在于候选农户的数量和每一个农户的生产能力。农户的数量从10、20、30户增加到150户，间隔为10户，分别对应16个算例。每个算例中，单个农户的生产能力为2倍的需求除以农户的数量。

3.2 GA与PSO算法比较

为了对两种算法的计算效能进行比较，选取算法终止时获得的最小成本和所用时间为评价指标。在相同终止条件下，算法终止时的最小成本反映了算法的求解精度，成本值越小，算法求解精度越高；所用时间反映了算法的效率，时间越短，效率越大。

根据算例的参数特征和多次试算结果，确定算法参数。其中，遗传算法关键参数取值如下：二进制位数11，交叉概率1.0，变异概率0.0003，约束违背惩罚系数1.0E+05，停止迭代的标准差为100，最大迭代次数为2 500次。粒子群算法关键参数取值如下：惯性权重c1=2.5、c2=2.0，速度上限为8.0，约束违背惩罚系数为1.0E+05，停止迭代的标准差和最大迭代次数与遗传算法相同。GA和PSO算法程序用MATLAB的M语言编写，所有计算在Intel（R）core（TM）i5-2410M CPU@2.30GHz处理器、4GBRAM的计算机上完成。在上述参数和条件下，不同规模算例两种算法的计算结果如图1和图2所示。

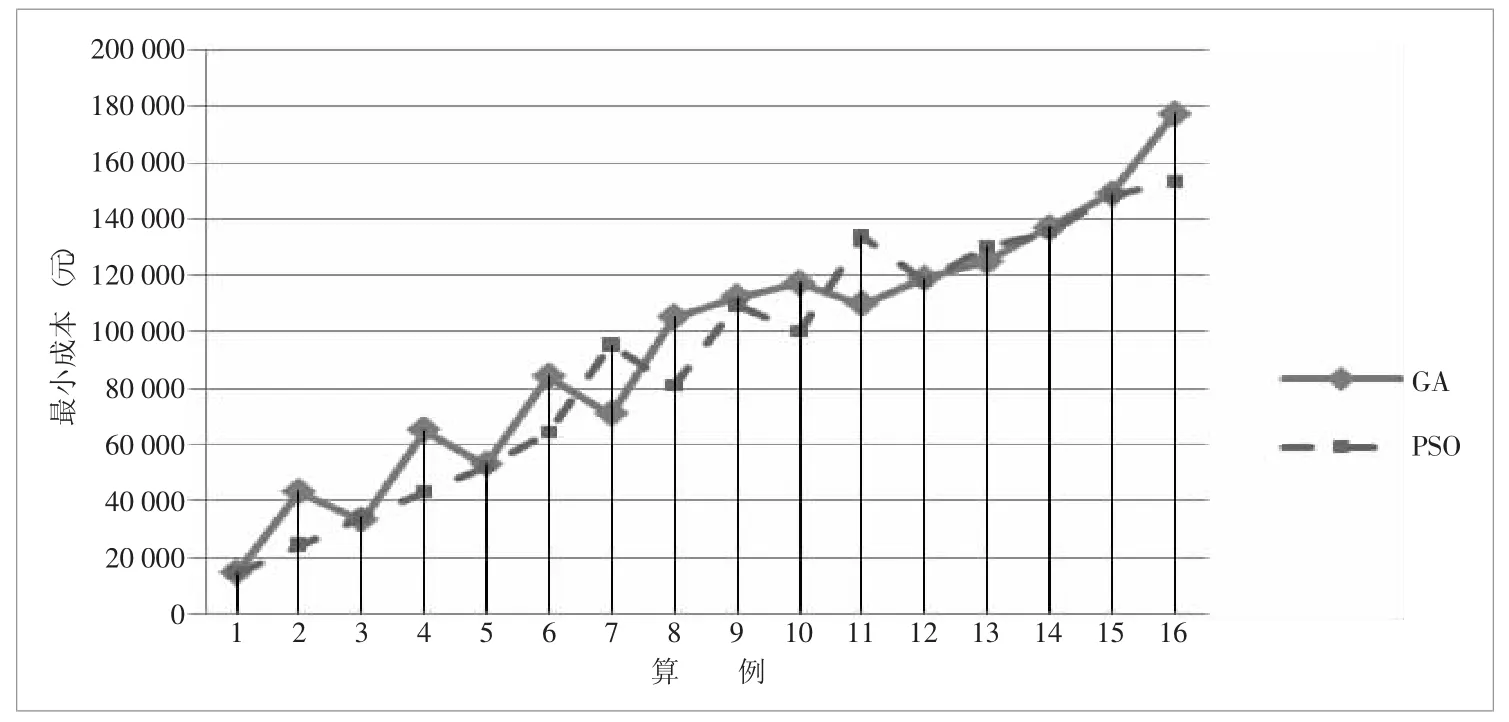
图1 GA和PSO算法在寻优能力上比较

从寻优能力来看（图1），PSO算法明显要优于GA。在16个算例中，算例1、2、4、5、6、8、9、10、12、14、15、16采用PSO算法获得的最小期望成本要小于GA，占到了总数的75%。在这些算例中，PSO算法的最小成本值小于GA的程度最大为43.8%，最小为0.2%。同时，这些算例中既有小规模算例如算例1、2、4，也有较大规模算例如14、15、16，表明PSO算法寻优能力上的优势并不受问题规模的影响。

图2 GA和PSO算法在时间效率上比较

从计算时间效率来看（图2），GA收敛的速度明显优于PSO算法。除算例1、2、3、6外，其余12个算例GA停止迭代的时间均小于PSO算法，占比达到75%。这些算例中，PSO算法所用时间比GA最大多出670s，最小为17s，而且随着算例规模的增大，GA所用时间都要小于PSO算法。

综合来看，有9个算例（占比为56.3%）PSO算法以较长的时间获得了更小的成本；有3个算例（占比为18.7%）PSO算法以更短的时间获得了更小的成本；有3个算例PSO算法用了更多的时间却得到了更大的成本；有1个算例（占比为6.3%）PSO算法用时虽短但得到的成本更大。值得注意的是在第一种情况的9个算例中，虽然PSO算法用时比GA多，但多出时间的最大值仅为670s，是在可接受范围内。因此，综合考虑算法的寻优能力和时间效率，PSO算法更适合于求解所建立的模型。

3.3 农户供应不确定的影响

选取总签约量和期望成本两个指标反映农户实际供应不确定的影响。具体的做法是改变农户实际供应比例的均值和标准差，分别计算在不同均值和标准差组合下总的签约量和最小期望成本。此处，以算例2的参数为基准，采用PSO算法求解。

（1）对总签约量的影响

农户供应不确定对总签约量的影响如图3所示。从图3中可以看出，在不同的供应比例均值和标准差取值下，总的签约量都是大于实际需求的。其中，当实际供应比例均值不超过0.65时，总签约量最小（2 003kg），比实际需求多3kg；当标准差为0.16，均值为0.8时，总签约量最大，达到2 811kg，比实际需求多811kg。这说明农业企业在面对农户供应不确定时，为了实现期望成本最小，应该与农户订购比实际需求更大的量。另外，随着供应比例均值的增加，总签约量先增大后减小，而不是单纯的降低；随着供应比例标准差的增加，总签约量会增大。这表明：一方面农户供应不确定对总签约量的影响是非线性的；另一方面农户供应不确定性越大，企业需要订购更多的量来防范供应不稳定风险。

（2）对最小期望成本的影响

农户供应不确定对最小期望成本的影响如图4所示。从图4中可以看出：随着农户实际供应比例均值的增加，最小期望成本呈现下降的趋势；随供应比例标准差的增大，最小期望成本呈增大趋势，但增加的速度不大。在不同的供应比例标准差取值下，当实际供应比例均值从0.5提高到1.0时，最小期望成本降低的程度均超过了50%；当供应比例均值在0.7以下时，随着供应比例标准差从0.08提高到0.16，最小期望成本没有发生明显变化；当供应比例均值在0.75以上时，随着供应比例标准差从0.08提高到0.16，最小期望成本平均增加约2.4%。这表明：提高农户实际供应数量水平和稳定性，都有利于降低企业的成本；比较而言，提高农户实际供应数量水平对降低企业成本效果更显著。

图3 农户供应不确定对总签约量的影响

4 结论

本文针对订单农业供应链中农户实际供应量与签约量不一致的问题，从农业企业角度提出事前风险控制策略，建立供应不确定下农户选择及订单分配模型，设计求解模型的GA和PSO算法，通过算例对两种算法性能进行了对比，分析了农户供应不确定对总签约量和最小期望成本的影响。研究得到的主要结论如下:（1）综合考虑算法的寻优能力和时间效率，PSO算法更适合于求解所建立的农户选择及订单分配模型；（2） 为了应对农户实际供应不确定，企业与农户的签约量应大于实际的需求；（3） 农业企业的总签约量和最小期望成本随农户实际供应不稳定程度的增加而增大，随实际供应数量水平的提高而降低；（4）相对于减少农户实际供应的波动性，提高农户实际供应数量水平，更有利于企业降低成本。

然而，在订单农业供应链的实际运营中，农业企业不仅要面对农产品供应不稳定的风险，而且还要承担巨大的市场风险。因此，在未来的研究中，可将需求的不确定纳入决策模型中。另外，当农业企业是风险厌恶或风险喜好时，对农户的选择和订单分配决策又有什么样的影响，也值得进一步研究。

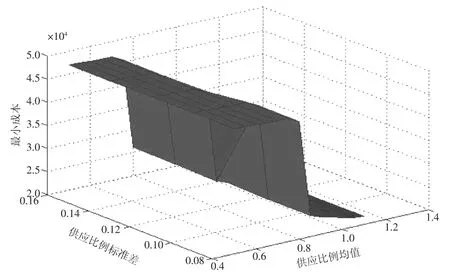
图4 农户供应不确定对最小期望成本的影响