基于改进支持向量机算法的水质监测模型研究

郭 英

（河北省唐山水文水资源勘测局，河北 唐山063000）

城乡经济的快速发展，伴随着污染物的大量排放。加之对污染物的治理措施及管理制度落后，导致水体污染严重，河流生态环境急速下降，严重威胁到水中动植物甚至城乡居民的生命安全，需找出合理的治理措施提高水体水质[1]。现如今，通过水质历时监测数据，找出其中规律，建立水质监测模型，是水环境研究工作和污染治理工作的基础，已逐渐成为了相关部门研究的热点之一[2]。长期对水质进行监测，操作成本高，在偏远地区无法实现，因此，研究水质监测模型具有重要意义[3]。

由于水环境系统涉及到了温度、气候、化学、人为因素等多个方面，是较复杂且较稳定的系统，水质随施加变化是存在一定规律性的[4]。机器学习神经网络模型可通过对基础数据的长时间训练，找出数据内在的规律，达到预测数据的目的，因其原理简单，计算结果精确，已被大量应用于预测模型的建立中[5]。郭小青和项新建[6]基于神经网络模型建立了水质监测及评价系统，验证了人工神经网络模型的精确性；李晓东等[7]同样通过人工神经网络模型建立了水质监测模型，结果精确度较高。

人工神经网络BP模型和支持向量机SVM模型是应用较广泛的机器学习模型。但BP模型虽具有一定的自适应能力，但其存在学习能力弱、收敛速度较慢、易出错等诸多问题，限制了其应用推广[8]。而SVM模型同样存在无法估计预测不确定性的问题，导致其精度较低[9]。本文拟将SVM进行改进，针对具体水质指标长时间实测数据，以水中总磷、总氮、化学需氧量和溶解氧含量为基础，研究改进SVM模型、SVMM模型计算精度，并与BP模型和SVM模型计算结果进行对比，找出最优水质监测模型。

1 研究方法

1.1 BP人工神经网络模型

根据图1所示的神经网络拓补结构，可知BP神经网络为非线性函数。当输入节点数为n，输出节点数为m时，神经网络模型表达了输入节点到输出节点的映射关系[10]。BP神经网络模型需首先训练模型，其具体计算步骤见文献[11]中的描述。

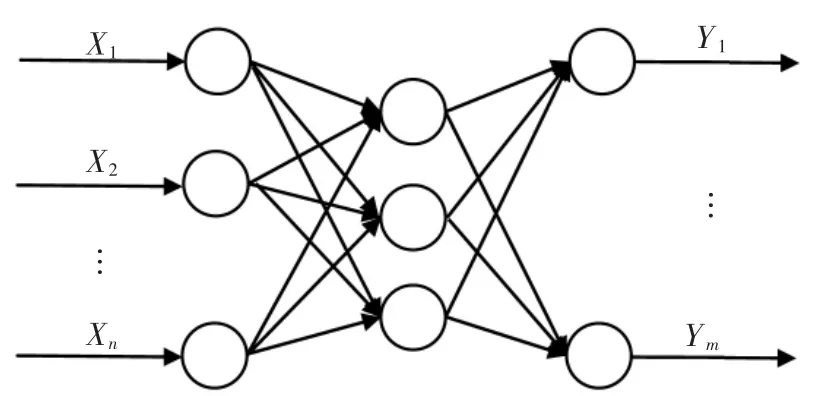
图1 BP神经网络计算原理

1.2 改进SVM模型建立[12]

SVM模型与BP神经网络模型类似，均是通过训练数据，找出数据中存在的内部规律，从而对未来数据进行预测，SVM模型具体计算步骤见文献[12]。粒子群算法（PSO）可用粒子的位置代替解的值，每粒子可由其大小和方向决定其速度矢量，其粒子的速度和位置可由迭代方法计算求得，其计算公式：

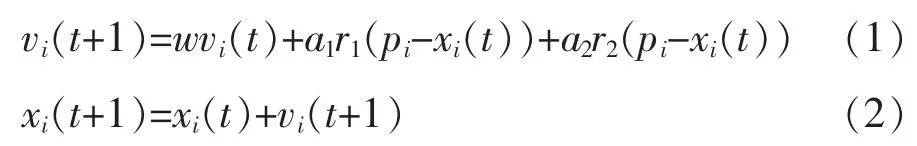
式中vi（t+1），vi（t）分别为粒子在t+1和t时刻的速度；xi（t+1），xi（t）分别为粒子在t+1和t时刻的位置；ω为指标权重；a1，a2为学习因子，取值在[0，2]之间；r1，r2为随机系数，取值在[0，1]之间。

基于PSO原理对SVM模型进行优化，首先对SVM模型中的参数进行优化，根据SVM中的核函数，优化确定SVM模型中的参数值，根据每个粒子的适应度，确定每个粒子的最优位置，由最优粒子代替原有粒子，得出SVM模型最优参数，提高SVM模型的计算精度[13]。

1.3 误差指标计算

判断预测模型计算精度的指标有很多，比如相对误差、绝对误差等。经过相关研究的长时间表明，在判断模型计算精度时，应从计算结果与实际值的误差及一致性两个方面综合考虑。Nash-Sutcliffe系数CD、相对误差RE和Kendall一致性系数K可以较好地反映长时间预测序列与实测值的误差和一致性，是系统性较好的数据评价指标体系。其中，CD与K的值越大、RE的值越小，模型算法与实测值的一致性越好、计算精度越高，具体公式：

式中 P′为模型算法模拟值；Pm为实测值；Pm为实测值的均值；n为样本数量；C为待检验方法与实测结果中拥有一致性元素的对数；D为待检验方法与实测结果中不具有一致性元素的对数。

2 结果与分析

2.1 不同模型模拟结果日值与实测值拟合方程斜率对比分析

表1为不同模型日值模拟结果与实测数据的拟合方程斜率与决定系数。

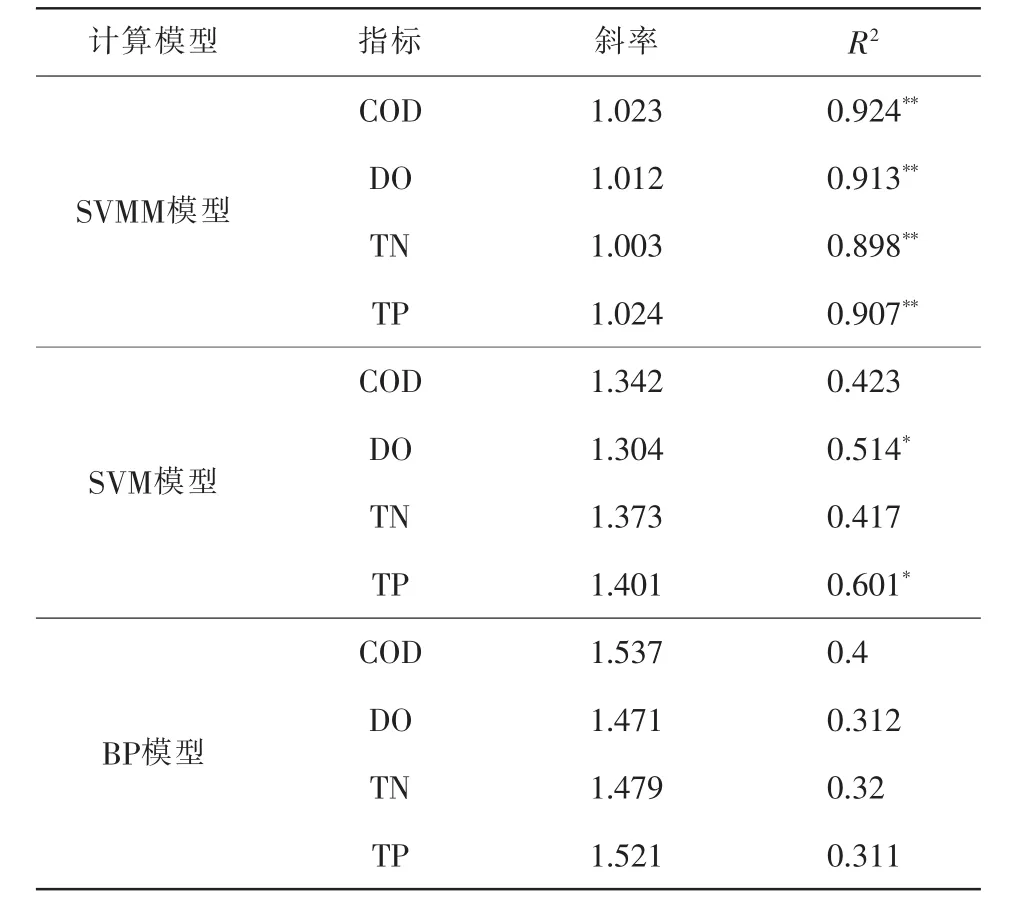
表1 不同模型模拟结果日值与实测值拟合方程斜率

表1显示，模型改进后，在模拟计算4种指标时的精度和一致性均有很大提高。由表1可知，3种模型均高估了4项水质指标值，其中BP模型计算精度最差，其与实测值拟合方程斜率最高达到1.537，而决定系数R2均在0.5以下，且与实测值的相关性均未达显著水平（P＞0.05）；SVM模型虽计算精度较BP模型略有提高，但精度仍较差，在估算TP时，虽决定系数R2的相关性达到显著水平（P＜0.05），但拟合方程斜率达到1.401，精度较差；SVMM模型计算精度最高，4项指标拟合方程斜率均较接近于1，且决定系数R2均达到0.8以上，同时与实测数据的相关性达到极显著水平（P＜0.01）。综上所述，在模拟水质日值时，SVMM模型模拟结果表现出了较高的精度和一致性。

2.2 不同模型模拟结果月值趋势分析

图2为不同模型模拟结果与实测值月值趋势分析。

图2 不同模型模拟结果月值与实测值趋势分析

图2显示，不同水质指标在年内的变化趋势呈现了明显的抛物线型式，均呈现出由升高到降低的变化趋势。不同模型模拟DO含量时，SVMM模型与实测值变化趋势基本一致，且数值相近，而BP模型和SVM模型均在很大程度上高估了DO值，平均误差分别达到59.3%和64.7%；在模拟COD时，SVMM模型与实测值误差仅为11.4%，而BP模型与SVM模型与实测值误差分别达到71.4%和69.8%；在模拟TP时，SVMM模型与实测值误差仅为9.8%，而BP模型与SVM模型与实测值的误差分别达到58.4%和64.2%；在模拟TN时，SVMM模型与实测值误差仅为7.6%，而BP模型与SVM模型与实测值误差分别达到56.4%和61.2%。综上所述，在模拟水质指标月值时，SVMM模型模拟精度最高。

2.3 不同模型模拟结果精度指标对比

表2为不同模型模拟结果与实测值的精度指标对比分析。

表2 不同模型模拟结果与实测值精度指标对比

表2显示，SVMM模型对水质指标进行模拟时，计算误差最低，其RMSE值虽在模拟TN时较高，但仅为0.207，模拟其余指标时，RMSE均低于0.2，而其模拟结果与实测值的一致性最高，K值与CD值均在0.80以上，且与实测值的相关性均达到了极显著水平 （P＜0.01）；SVM模型模拟结果较差，RMSE值普遍在0.4～0.5之间，误差较高，反映一致性的指标K值与CD值在0.4～0.6之间，且K值在除了模拟TN时，CD值除了模拟COD时，其余指标均达到了显著水平（P＜0.05）；BP模型的模拟精度最差，RMSE值均在0.65以上，误差最高，K值与CD值均在0.5以下，且与实测值的相关性均未达显著水平（P＜0.05）。综上所述，SVMM模型的模拟精度最高，SVM模型次之，BP模型最差，与前文结论基本一致。

3 结语

基于PSO算法优化SVM模型（SVMM），以4种水质指标实测值为基础，以期模拟水质指标，得出用于水质监测的模型，将得出的结果与BP神经网络模型、SVM模型做了对比，最终结论可知，在对模拟结果日值、月值和精度指标进行分析后，可知SVMM模型的模拟精度最高，该模型可称为水质监测的基本模型使用。