矩形截面偏心受压构件对称配筋设计判别大小偏心时分歧的探讨研究

谢立安

（山西省交通科学研究院 桥梁工程防灾减灾山西省重点实验室 黄土地区公路建设与养护技术交通行业重点实验室，山西 太原 030006）

当前，矩形截面偏心受压构件对称配筋设计时，对于如何判断大小偏心，主要有以下两种方法：

a）当 ei＞0.3h0且 ξ≤ξb时为大偏心受压；当 ei≤0.3h0，或 ei＞0.3h0且 ξ＞ξb时为小偏心受压[1]。

b）当 ξ≤ξb时为大偏心受压；当 ξ＞ξb时为小偏心受压[2]。

仔细分析上述两种方法后，发现当ei＞0.3h0时，两种方法判别结果相同，但当ei≤0.3h0时，两种方法判别结果将存在分歧，表现在当ei≤0.3h0且ξ≤ξb时，第1种方法判别结果为小偏心受压，而第2种方法判别结果为大偏心受压，因此两种方法间存在的分歧可能会导致完全不同的计算结果。下面运用算例、判别条件的数值解法和判别条件的图解法来说明两种方法间的差别和适用性。

1 算例

例题：某矩形钢筋混凝土偏心受压构件，截面尺寸为b×h=400 mm×600 mm，混凝土强度等级为C30 混凝土（fc=14.3 N/mm2，α1=1.0，β1=0.8），纵向钢筋 为 HRB400 级 钢 筋 （fy=f′y=360 N/mm2,ξb=0.518），纵向钢筋至截面近边缘距离为 as=a′s=40 mm，截面有效高度h0=560 mm，控制截面上轴向压力设计值 N=1 500 kN，对应的弯矩设计值 M=60 kN·m（已考虑二阶效应）。试按对称配筋选择钢筋As和A′s.

解析：依据第1种方法进行求解：

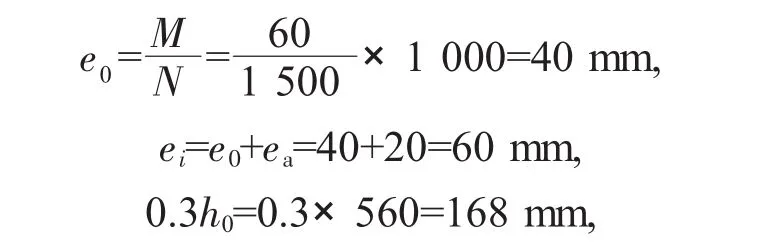
由ei≤0.3h0，判别为小偏心受压。

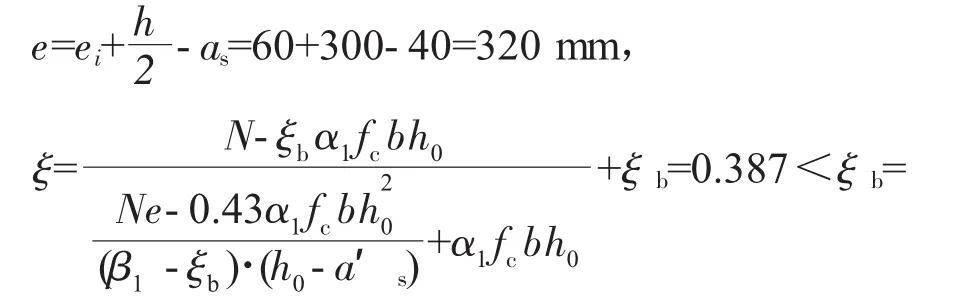
0.518 ，说明不满足小偏心受压条件。

下面依据第2种方法进行求解：

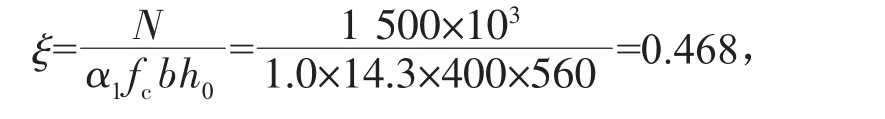
由 ξ＜ξb，判别为大偏心受压。

依据规范[3]第8.5.1条规定，受压构件全部纵向钢筋最小配筋率为0.55%，一侧纵向钢筋最小配筋率为0.2%。若按每侧配筋率为0.275%进行配筋，则全部纵向钢筋最小配筋率和一侧纵向钢筋最小配筋率均满足要求，此时

下面对A′s=As=660 mm2进行复核，以证明第2种方法求解结果可用。

a）情况1 已知N求M.

假定为大偏心受压构件，则：

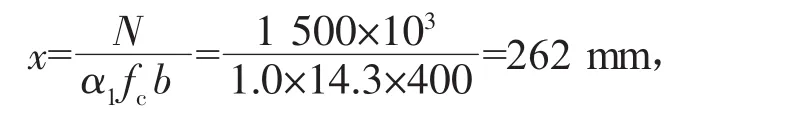
且 2α′s=2×40 mm=80 mm＜x=262 mm ＜ξbh0=0.518×560=290 mm，说明满足大偏心受压条件。

M=Ne0=1 500×231×10-3=347 kN·m＞60 kN·m，满足要求。

b）情况2 已知e0求N.

假定为大偏心受压构件，则：

联立消去N并代入数据后，可得：

x=557 mm＞ξbh0=0.518×560=290 mm，说明不满足大偏心受压条件，应按小偏心受压条件进行计算。

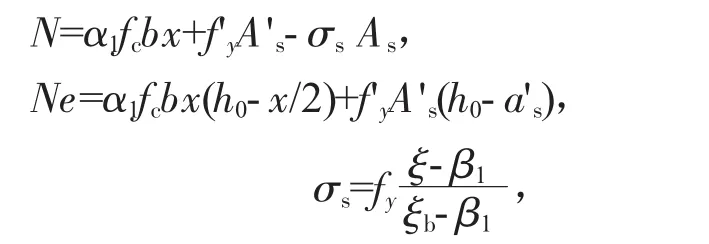
联立消去N并代入数据后，可得：

x=505 mm＞ξbh0=0.518×560=290 mm，满足小偏心受压条件。

N=α1fcbx+f′yA′s-σsAs=3 212 kN＞1 500 kN，满足要求。

2 判别大小偏心的数值解法

由以上算例可以看出，采用第1种方法判别大小偏心时可能会出现误判，而采用第2种方法判别大小偏心时会得出正确结果。

事实上，采用第2种方法判别大小偏心是依据大小偏心受压的定义、破坏特征和界限条件[1-2]得出，是不会发生误判的，而依据第1种方法判别大小偏心是可能会出现误判的，这需要从用ei≤0.3 h0直接确定为小偏心受压的推导过程去解释。具体推导过程如下[1]。

取界限破坏情况下受压区高度x=ξbh0代入大偏心受压基本平衡方程中，并取as=a′s，可得界限破坏时的轴向力Nb和对截面几何形心轴的弯矩Mb：

此时的偏心距（即对截面几何形心轴的偏心距）可称为界限偏心距eb，则相对界限偏心距eb/h0为：

分析上式可知，当截面尺寸和材料强度均确定时，亦即ξb为定值，则相对界限偏心距就是As和A′s的二元函数，且随As和A′s的减小而减小。当As和 A′s按最小配筋率 ρmin和 ρ′min取值时，相对界限偏心距将取得理论最小值。因此当时就属于小偏心受压。如果依据规范取ρmin=ρ′min=0.2%，并取 h=1.05h0，as=a′s=0.05h0，即可得常用等级混凝土和HRB335级及HRB400级钢筋的理论相对界限偏心距最小值，如表1所示。

表1 理论相对界限偏心距最小值

由表1可以看出，对于常用等级混凝土和HRB335级及HRB400级钢筋的理论界限偏心距最小值eb，min均在0.3h0左右，于是就近似0.3h0取作为大小偏心受压的界限。

事实上，上述推导过程中忽视了两个重要问题：

a）当 As和 A′s按最小配筋率 ρmin=ρ′min=0.2%取值时，虽然满足了规范一侧纵向钢筋最小配筋率要求，却不满足规范全部纵向钢筋最小配筋率要求，导致上述理论界限偏心距最小值eb,min取0.3h0偏低，这就使得用ei＞0.3h0直接确定为大偏心受压时会出现误判，因此必须附加截面相对受压区高度ξ和界限受压区高度ξb间的关系，而在用ei≤0.3h0直接确定为小偏心受压时似乎不会出现误判，但却忽略了下述第2个重要问题，即荷载较小时的状况。

b）当荷载较小时，按照平衡方程在理论上求解会得到配筋值As和A′s很小甚至为负值的情况（如前算例中得到的 A′s=As=-870 mm2＜0），此时满足规范最小配筋率要求的理论界限偏心距最小值eb,min将仍由上述推导公式给出，但不考虑规范最小配筋率要求的实际界限偏心距最小值e′b,min，由于具有随As和 A′s配筋率 ρmin和 ρ′min减小而减小的特点，显然会比0.3h0低（仅从数学角度看，这种情况是完全可能存在的），即实际界限偏心距最小值e′b,min＜0.3h0，于是就会出现满足 ei＜0.3h0而不满足 ei＜e′b,min的现象，而这种现象显然按大偏心受压计算是合适的。

综上所述，按照ei和0.3h0间的关系来判别大小偏心受压时，必须附加截面相对受压区高度ξ和界限受压区高度ξb间的关系，否则就可能会出现误判。

3 判别大小偏心的图解法

依据钢筋混凝土受弯构件斜截面承载力计算中确定纵向受拉钢筋弯起位置时抵抗弯矩图的概念，可得钢筋混凝土偏心受压构件的N-M相关曲线实际上相当于该偏心受压构件在某种配筋率ρ条件下的N-M抵抗图，曲线上任一点的坐标代表截面承载力中N和M的一种组合。如任意点P位于曲线内侧，说明截面在该点坐标给出的内力组合下并未达到承载能力极限状态，相反如任意点P位于曲线外侧，说明截面在该点坐标给出的内力组合下承载能力不足。因此通常情况下，配筋率ρ较大的N-M相关曲线将位于配筋率较小的N-M相关曲线的外侧，当截面尺寸和材料强度均确定时，亦即ξb为定值，即各条曲线的界限受压区高度ξb相同，对应的界限破坏时的轴向力Nb=α1fcbξbh0也相同，如图1所示。

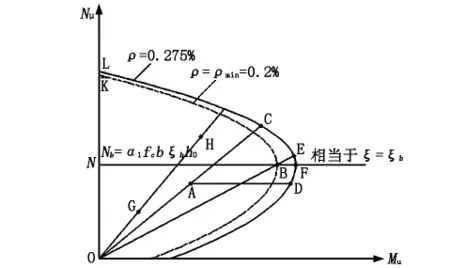
图1 对称配筋偏心受压构件的N-M相关曲线

3.1 配筋设计

当采用第2种方法判别大小偏心时，直线N=Nb（相当于ξ=ξb）将N-M相关曲线分为上下两部分，上部分为小偏心受压，下部分为大偏心受压，而不会出现误判。

当采用第1种方法判别大小偏心时，由于N-M相关曲线中Mu=Nueu，故OB线的斜率为1/euB，那么在配筋率ρ=ρmin=0.2%的N-M相关曲线上，小偏心受压点（即曲线BK上的点）与原点连线的斜率均大于OB线的斜率，即这些点对应的偏心距eu均小于点B的偏心距euB，而点B的偏心距euB正是前述公式中推导出的满足规范最小配筋率要求的理论界限偏心距最小值eb,min。由于各条曲线的Nb值（相当于ξb值）相等，故在配筋率ρ＞ρmin=0.2%的N-M相关曲线族中，除其上部区域（如区域BKLE）中点的eu小于eb,min必为小偏心受压外，还有部分区域（如区域BEF）中的点也为小偏心受压。基于此可知，当任意点P位于配筋率ρ=ρmin=0.2%的N-M关曲线的外侧时，也就是荷载较大时的情况，当ei＜0.3h0时必为小偏心受压，但ei＞0.3h0时就未必全部是大偏心受压，也可能是小偏心受压；而当任意点P位于配筋率ρ=ρmin=0.2%的N-M相关曲线的内侧时，也就是荷载较小时的情况，如图中的G点和H点，可知此时只需按构造要求进行配筋即可，且G点的偏心距eG和H点的偏心距eH相等并均小于0.3h0，但很明显G点为大偏心受压，而H点却为小偏心受压，此时若仅依据ei＜0.3h0而将G点和H点均判别为小偏心受压时，对于G点将会出现误判，通过分析发现，这种误判将主要集中于N≤Nb（相当于ξ≤ξb）的区域ONB中。综上所述，按照ei和0.3h0间的关系来判别大小偏心受压时，必须附加截面相对受压区高度ξ和界限受压区高度ξb间的关系，否则就可能会出现误判。

3.2 截面复核

截面复核时，算例中已知条件是点A的坐标（N，M）和配筋率ρ=0.275%的N-M相关曲线。对照图1，若已知N求M，则实际上试求D点对应的Mu，由于N＜Nb，所以是大偏心受压（算例中情况1中x＜ξbh0说明了这一点）；若已知e0求N，则实际上是求C点对应的Nu，此时直线OC的斜率1/ei为关键因素，由于ei＜0.3h0，所以是小偏心受压（算例中情况2中x＞ξbh0说明了这一点）。

4 结论

a）按照第1种方法，即ei和0.3h0间的关系来判别大小偏心时，必须附加截面相对受压区高度ξ和界限受压区高度ξb间的关系，否则就可能会出现误判；而按照第2种方法，即直接用截面相对受压区高度ξ和界限受压区高度ξb间的关系判别大小偏心时，却不会出现误判。因此实际矩形截面偏心受压构件对称配筋设计时可直接用第2种方法来判别大小偏心。

b）当荷载较小且满足ei≤0.3h0时，按照规范给出的小偏心受压构件相对受压区高度ξ计算公式求解时，会发现求解出的相对受压区高度ξ不满足小偏心受压条件，此时就意味着发生了误判，需要按大偏心受压条件进行求解。

c）理论界限偏心距最小值eb,min=0.3h0是基于规范一侧纵向钢筋最小配筋率要求推导出来的，当进行截面复核已知e0求N时，由于截面配筋肯定满足规范一侧纵向钢筋最小配筋率要求和规范全部纵向钢筋最小配筋率要求，此时直接用ei≤0.3h0判别为小偏心是合适的。