2018年高考理综全国Ⅰ卷第25题的解法探析

周伟波

(广东番禺中学，广东 广州 511400)

2018年理综全国Ⅰ卷第25题以考生熟悉的“电磁组合场”为背景,通过类平抛运动、匀速圆周运动、数学几何、功能关系等知识规律的综合,全面考察了考纲所要求的理解能力、分析推理能力、以及应用数学处理物理问题的能力.同时,也充分渗透了新课标所倡导的物理观念、科学思维等学科核心素养.

1 真题呈现

图1

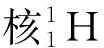
(2) 磁场的磁感应强度大小;

图2

2 牛顿定律与几何关系相结合的解法

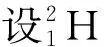
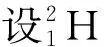
联立以上各式解得

点评:本解法采用动力学公式和数学几何相结合的常规方法.基本公式、规律、模型,学生是比较熟悉的,但由于物理量众多,公式关系复杂,数学能力要求较高,从而导致学生思维混乱,难以下手.

3 二级推论与功能关系相结合的解法

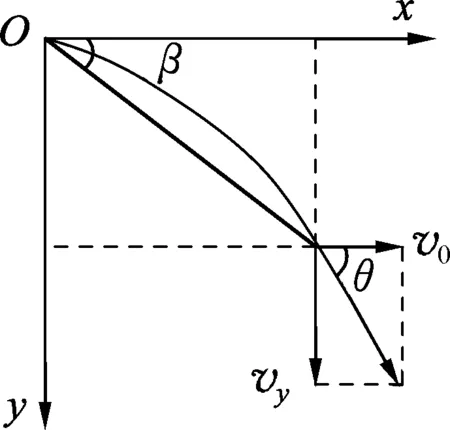
图3

(1) 推论1:如图3,平抛运动中,速度偏向角θ的正切值等于位移偏向角β的正切值的2倍,即tanθ=2tanβ.

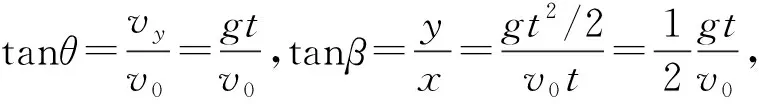
图4

图5

推论2:如图5,平抛运动中,任何时刻瞬时速度的反向延长线一定通过此时水平位移的中点.

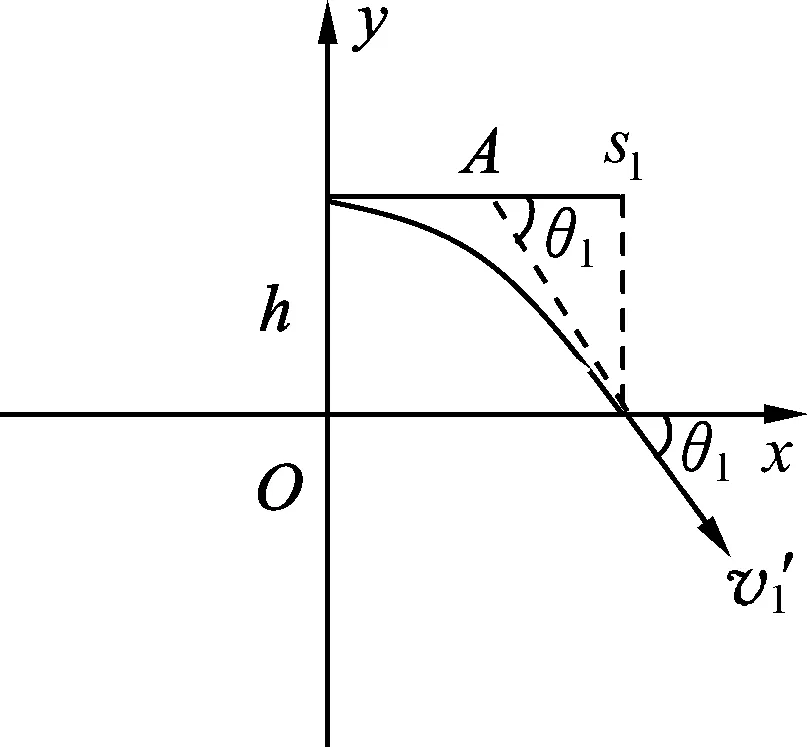
图6

(3) 推论3:不同比荷的带电粒子,从静止释放,经过相同的加速、偏转电场后,将会在同一位置、同一方向射出.

图7

点评:本解法中,二级推论具有“一锤定音”的神奇效果,但直接套用二级推论得出答案的做法是绝不允许的.如果考生平时能把二级推论的应用条件、证明过程都熟练掌握了,就能实现“以推论给题目定调”,“把证明过程渗透到解题中”的 “一箭双雕”的快速解题效果.本解法中还利用了动能定理得出两粒子在进入磁场中时具有相同动能,从而快速判断两者速度大小乃至轨迹半径的比例关系,此做法也是令人爽心悦目的.

4 抛物线方程与物理规律相结合的解法

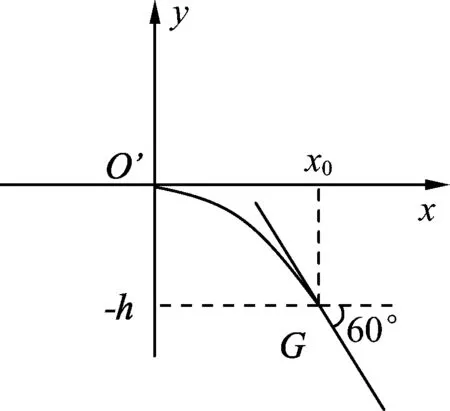
图8

(1) 如图8所示,以原y轴出射点(设为O′)为新坐标原点,重新建立数学直角坐标系.

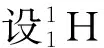
设抛物线方程为y=ax2(a为常数,由于抛物线开口向下,故a<0),把(x0,-h)代入抛物线方程得-h=ax02.

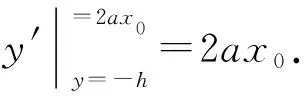
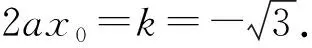
由以上各式解得

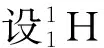
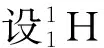
剩下解答与牛顿定律与几何关系相结合(或二级推论与功能关系相结合)的解法相同,过程略.

点评:本解法在尊重物理规律的基础上另辟新路,巧妙利用数学的抛物线方程、导数和切线斜率的关系,把物理量之间纵横复杂的关系变为一目了然的数学方程.因此,正如高考考纲明确要求的,提高考生应用数学处理物理问题的能力,是往后课堂教学的一个努力方向.

5 思考与启示

综合来看,本高考压轴题的模型考生是有亲切感的,它源于日常训练的经典考题,但又不失风格,有自己的魅力之处,值得细细回味.上述的3种解法,从常规动力学观点到二级推论与功能关系,最后抛物线方程求解,实现了由常规的思维方式向深层的高阶思维方向转变和跃迁.也启示我们在日常的课堂教学中,特别是培优教学,既要落实好常规的主干知识,又要通过对二级推论的证明总结来加强常规考点的深化,更要重视应用数学处理物理问题的能力的培养,从而真正对学生实现学科核心素养的完美渗透.